在海杂波背景下,如何有效检测海上运动目标是海用雷达信号处理算法设计时需要解决的重点和难点问题[1, 2]。在过去的数十年里,已有大量研究人员围绕该问题开展研究,其中,相干积累检测方法因同时利用了回波的局部功率和多普勒信息而得到广泛关注。由于相干检测器中的海杂波协方差矩阵通常未知,需要利用邻近参考单元数据估计并替换,由此得到的检测器即为自适应检测器。
海杂波和目标模型的建立是自适应检测器设计时面临的基本问题之一[3]。若模型失配,则检测性能将出现一定的损失。对于海杂波,在低分辨率条件下高斯模型即可满足建模精度需求,而在较高分辨率条件下,建立在复合表面理论(Composite Surface Theory, CST)基础上的复合高斯模型得到广泛应用,其兼具物理机理层面的可解释性和数学层面的易操作性,且在支撑检测器设计方面具有一定的灵活性[4, 5]。对于目标,秩1模型的应用较为普遍,其主要优势在于结构简单,然而模型仅包含一个自由度,在描述海上目标的复杂运动状态方面具有一定的局限性。例如,海面舰船的运动状态除包含平动分量外,还存在沿俯仰、横滚等方向的转动分量,因此在特征空间具有多个自由度。此时更加适合采用子空间模型建模目标信号,该模型还同时适用于描述目标状态的不确定性和多径效应[6-8]。
目前,高斯背景下秩1目标和子空间目标的自适应检测问题均得到了较为深入的研究[9-15],较有代表性的检测器包括自适应匹配滤波(Adaptive Matched Filter, AMF)检测器、自适应子空间检测器(Adaptive Subspace Detectors, ASD)等。在复合高斯背景下,围绕秩1目标的研究较为深入[16-20],其中,自适应归一化匹配滤波(Adaptive Normalized Matched Filter, ANMF)检测器较为典型;相比之下,子空间目标的自适应检测问题研究较少,尽管相关文献推导了检验统计量[3],但是对纹理分量的先验分布信息利用不充分。在工程实践中,这种先验信息可从大量海杂波统计分析得到的离线数据库中获取,也可由雷达工作时获取的实测数据中实时感知得到。经已有研究证实[21],若检测器设计时有效利用这种先验信息,将改善检测器与背景之间的匹配程度,有助于检测性能提升。
立足于上述背景,本文在考虑纹理分量先验分布模型的前提下研究子空间目标的自适应检测问题。考虑到逆Gamma (Inverse Gamma,
考虑一个天线阵元的情况,假定在一个相干处理间隔(Coherent Processing Interval, CPI)内发射N个脉冲,接收机对回波信号进行解调、匹配滤波和采样,那么单个距离单元的观测数据为N×1维复矢量。所要解决的目标检测问题可描述为如下的二元假设检验:
| $\left\{ \begin{array}{l} {{\rm{H}}_0}:{\rm{ }}\mathit{\boldsymbol{z}} = \mathit{\boldsymbol{c}}, \ {\rm{ }}{\mathit{\boldsymbol{z}}_k} = {\mathit{\boldsymbol{c}}_k}, \ {\rm{ }}k = 1, \cdots, K\\ {{\rm{H}}_1}:{\rm{ }}\mathit{\boldsymbol{z}} = \mathit{\boldsymbol{s}} + \mathit{\boldsymbol{c}}, \ {\rm{ }}{\mathit{\boldsymbol{z}}_k} = {\mathit{\boldsymbol{c}}_k}, \ {\rm{ }}k = 1, \cdots, K \end{array} \right.$ | (1) |
其中,z和zk表示检测单元和参考单元的观测数据,c和ck表示检测单元和参考单元的海杂波,s为目标信号,K为参考单元数。
2.1 海杂波模型采用复合高斯模型建模海杂波,该模型可表示为散斑分量与纹理分量乘积的形式。由于纹理分量的相关时间较长,因此当观测时间在雷达系统的CPI量级时,纹理分量可建模为随机常数,此时海杂波观测数据构成球不变随机矢量(Spherically Invariant Random Vector, SIRV),即
| $\mathit{\boldsymbol{c}} = \sqrt \tau \mathit{\boldsymbol{x}}, \ {\mathit{\boldsymbol{c}}_k} = \sqrt {{\tau _k}} \mathit{\boldsymbol{x}}$ | (2) |
其中,τ和τk为纹理分量,与海杂波局部功率水平有关,且在不同距离单元之间通常具有一定的相关性[25]。
| ${p_\mathit{\boldsymbol{c}}}(\mathit{\boldsymbol{c}})\! = \! \!\int_0^\infty \!\!\!\!\!\! {\frac{1}{{{{(\pi \tau )}^N}\det (\mathit{\boldsymbol{M}})}}\!\exp \!\left(\! {\! - \frac{{{\mathit{\boldsymbol{c}}^{\rm{H}}}{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{c}}}}{\tau }}\! \right)\!\!p(\tau ){\rm d}\tau } $ | (3) |
其中,det(·)表示矩阵的行列式,
| $p(\tau ) = \frac{1}{\Gamma }(v){\left( {\frac{v}{\eta }} \right)^{v}}{\tau ^{ - (v + 1)}}\exp \left( { - \frac{v}{{\eta \tau }}} \right)$ | (4) |
其中,η和v分别为尺度参数和形状参数,它们与海杂波的功率水平和拖尾程度有关。
2.2 子空间目标模型采用多维线性子空间模型对海上运动目标进行建模[3],目标模型s表示为:
| $\mathit{\boldsymbol{s}} = \mathit{\boldsymbol{Ea}}$ | (5) |
其中,E是维数为N×r的导向矩阵,a是r×1维的幅度矢量。E包含了目标后向散射回波的所有多普勒特征信息,是表征目标响应的特征量。在检测器设计时,通常假定E已知,而a未知,其可建模为确定性未知矢量或复高斯随机矢量,两种情况分别对应1阶高斯(First Order Gaussian, FOG)和2阶高斯(Second Order Gaussian, SOG)目标模型[6],对于后者,a可表示为
根据上述模型,当纹理分量给定时,在H0假设下,观测数据矢量满足:
| $\mathit{\boldsymbol{z}}|\tau, {{\rm{H}}_0} \sim \mathcal {CN} ({\bf{0}}, \tau \mathit{\boldsymbol{M}})$ | (6) |
在H1假设下,FOG和SOG目标模型对应的观测数据矢量分别满足:
| $\mathit{\boldsymbol{z}}|\tau, {{\rm{H}}_1} \sim \mathcal {CN} ({{\mathit{\boldsymbol{U}}}_{\rm{S}}}{\mathit{\boldsymbol{b}}}, \tau \mathit{\boldsymbol{M}}) \ \ \ \ \ \ \ \ \ \ \ \ $ | (7) |
| $\mathit{\boldsymbol{z}}|\tau, {{\rm{H}}_1} \sim \mathcal {CN}({\bf{0}}, {\mathit{\boldsymbol{U}}_{\rm{S}}}{\mathit{\boldsymbol{R}}_{{{b}}}}\mathit{\boldsymbol{U}}_{\rm{S}}^{\rm{H}} + \tau \mathit{\boldsymbol{M}})$ | (8) |
根据Neyman-Pearson(NP)准则,最优检测器由似然比检验(Likelihood Ratio Test, LRT)给出,即
| $\lambda =\frac{\int_{0}^{\infty }{f{{}_{1}}(\mathit{\boldsymbol{z}}|\tau ,{{\rm{H}}_{1}})p(\tau )}\rm{d}\tau }{\int_{0}^{\infty }{f{{}_{0}}(\mathit{\boldsymbol{z}}|\tau ,{{\rm{H}}_{0}})p(\tau )\rm{d}\tau }}$ | (9) |
其中,
| ${\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} _0}:\left\{ \mathit{\boldsymbol{M}} \right\}, \ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} _1}:\left\{ {{b}, \mathit{\boldsymbol{M}}} \right\}$ | (10) |
而对于SOG目标模型,未知参数集合分别为:
| ${\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} _0}:\{ \mathit{\boldsymbol{M}}\}, {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} _1}:\left\{ {{{R}_b}, \mathit{\boldsymbol{M}}} \right\}$ | (11) |
对于FOG目标,即目标位置矢量b建模为确定性未知矢量的情况,GLRT表示为:
| $\frac{\mathop {\max }\limits_b \,\int_{0}^{\infty }{{{f}_{1}}(\mathit{\boldsymbol{z}}|\tau ,\mathit{\boldsymbol{b}},{{\rm{H}}_{1}})p(\tau )\rm{d}\tau }}{\int_{0}^{\infty }{{{f}_{0}}(\mathit{\boldsymbol{z}}|\tau ,{{\rm{H}}_{0}})p(\tau )\rm{d}\tau }}\underset{{{\rm{H}}_{0}}}{\overset{{{\rm{H}}_{\rm{1}}}}{\mathop{\underset{{>}}<}}}\,G$ | (12) |
其中
| ${f_1} = \frac{{{{(\pi \tau )}^{ - N}}}}{{\det \left( \mathit{\boldsymbol{M}} \right)}}\exp \left[{-\frac{{{{\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{U}}_{\rm{S}}}\mathit{\boldsymbol{b}}} \right)}^{\rm{H}}}{{{M}}^{-1}}( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{U}}_{\rm{S}}}\mathit{\boldsymbol{b}}} )}}{\tau }} \right]$ | (13) |
| ${f_0} = \frac{{{{(\pi \tau )}^{ - N}}}}{{\det \left( \mathit{\boldsymbol{M}} \right)}}\exp \left( { - \frac{{{{\mathit{\boldsymbol{z}}}^{\rm{H}}}{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{z}}}}}{\tau }} \right) \quad \quad \quad \quad \quad \ $ | (14) |
首先,利用分子部分得到b的最大似然(Maximum Likelihood, ML)估计值,估计结果为:
| ${{\hat {\mathit{\boldsymbol{b}}}}} = {({\mathit{\boldsymbol{U}}}_{\rm{S}}^{\rm{H}}{\mathit{\boldsymbol{M}}^{ - 1}}{{\mathit{\boldsymbol{U}}}_{\rm{S}}})^{ - 1}}{\mathit{\boldsymbol{U}}}_{\rm{S}}^{\rm{H}}{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{z}}}$ | (15) |
将其代入式(13),得
| $\mathop {\max }\limits_{{\mathit{\boldsymbol{b}}}} {f_1}({\mathit{\boldsymbol{z}}}|\tau, {{\hat {{b}}}}, {{\rm{H}}_1})\! = \!\frac{{{{(\pi \tau )}^{ - N}}}}{{\det \left( \mathit{\boldsymbol{M}} \right)}}\! \exp \left[{-\frac{{{{\mathit{\boldsymbol{z}}}^{\rm{H}}}({{\mathit{\boldsymbol{M}}}^{-1}} \!\!-\!\! {{\mathit{\boldsymbol{Q}}}}){\mathit{\boldsymbol{z}}}}}{\tau }} \right]$ | (16) |
其中,
| ${{{\boldsymbol{P}}}_{{{\mathit{\boldsymbol{M}}}^{ - 1/2}}{{\mathit{\boldsymbol{U}}}_{\rm{S}}}}} \!\!=\!\! {{\boldsymbol{M}}^{ - 1/2}}{{\mathit{\boldsymbol{U}}}_{\rm{S}}}{({\mathit{\boldsymbol{U}}}_{\rm{S}}^{\rm{H}}{\mathit{\boldsymbol{M}}^{ - 1}}{{\mathit{\boldsymbol{U}}}_{\rm{S}}})^{ - 1}}{\mathit{\boldsymbol{U}}}_{\rm{S}}^{\rm{H}}{{\boldsymbol{M}}^{ - 1/2}}$ | (17) |
令
| ${g_i} = \left\{ \begin{array}{l} {{\boldsymbol{z}}^{\rm{H}}}{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{z}}}, \quad \quad \quad \quad i{\rm{ = 0}}\\ {{\boldsymbol{z}}^{\rm{H}}}({\mathit{\boldsymbol{M}}^{ - 1}} - {{\boldsymbol{Q}}}){\mathit{\boldsymbol{z}}}, \quad {\rm{ }}i{\rm{ = 1}} \end{array} \right.$ | (18) |
将
| $\int_0^\infty {{f\!_1}({\boldsymbol{z}}|\tau, {{\hat {\boldsymbol{b}}}}, {{\rm{H}}_1})p(\tau ){\rm d}\tau } \propto {({g_1} + \beta )^{ - (v + N)}}$ | (19) |
| $\int_0^\infty {{f\!_0}({\boldsymbol{z}}|\tau, {{\hat {\boldsymbol{b}}}}, {{\rm{H}}_0})p(\tau ){\rm d}\tau } \propto {({g_0} + \beta )^{ - (v + N)}}$ | (20) |
其中,
| ${\left( {\frac{{{g_1} + \beta }}{{{g_0} + \beta }}} \right)^{ - (v + N)}}\mathop {\begin{array}{*{20}{l}} {\text{ > }} \\ {\text{ < }} \end{array}}\limits_{{{\text{H}}_0}}^{{{\text{H}}_{\text{1}}}} G$ | (21) |
式(21) 还可简化表示为:
| $\frac{{{\mathit{\boldsymbol{z}}}^{\rm{H}}}\mathit{\boldsymbol{Qz}}}{{{\mathit{\boldsymbol{z}}}^{\rm{H}}}{{\mathit{\boldsymbol{M}}}^{-1}}\mathit{\boldsymbol{z}}+\beta }\underset{{{\rm{H}}_{0}}}{\overset{{{\rm{H}}_{\rm{1}}}}{\mathop{\begin{align} & > \\ & < \\ \end{align}}}}\,G$ | (22) |
这即为FOG目标的GLRT检验统计量,在后续仿真时将其称之为FOG-GLRT。
3.3 SOG目标的GLRT对于SOG目标,即目标位置矢量b建模为零均值复高斯随机矢量的情况,GLRT表示为:
| $\frac{\mathop {max}\limits_{{\mathit{\boldsymbol{R}}_b}} ,\int_{0}^{\infty }{{{f}_{1}}(\mathit{\boldsymbol{z}}|\tau ,{{\mathit{\boldsymbol{R}}}_{b}},{{\rm{H}}_{1}})p(\tau )\rm{d}\tau }}{\int_{0}^{\infty }{{{f}_{0}}(\mathit{\boldsymbol{z}}|\tau ,{{\rm{H}}_{0}})p(\tau )\rm{d}\tau }}\underset{{{\rm{H}}_{0}}}{\overset{{{\rm{H}}_{\rm{1}}}}{\mathop{\begin{align} & > \\ & < \\ \end{align}}}}\,G$ | (23) |
其中
| ${{f}_{1}}=\frac{1}{{{\pi }^{N}}\det (\mathit{\boldsymbol{B}})}\exp (-{{\mathit{\boldsymbol{z}}}^{\rm{H}}}{{\mathit{\boldsymbol{ }}\!\!\Psi\!\!\rm{ }}^{-1}}\mathit{\boldsymbol{z}})$ | (24) |
| ${f_0} = \frac{{{{(\pi \tau )}^{ - N}}}}{{\det \left( \mathit{\boldsymbol{M}} \right)}}\exp \left( { - \frac{{{{\boldsymbol{z}}^{\rm{H}}}{\mathit{\boldsymbol{M}}^{ - 1}}{\mathit{\boldsymbol{z}}}}}{\tau }} \right)$ | (25) |
其中,
为简化推导过程,这里首先对观测数据做白化处理,白化后的检测问题表示为:
| $\left\{ \begin{array}{*{35}{l}} {{\rm{H}}_{0}}:\widetilde{\mathit{\boldsymbol{z}}}=\widetilde{c} \\ {{\rm{H}}_{1}}:\widetilde{\mathit{\boldsymbol{z}}}=\rm{ }\widetilde{s}+\widetilde{c} \\ \end{array} \right.$ | (26) |
其中,
| ${{\tilde {\boldsymbol{z}}}}|\tau, {{\rm{H}}_0} \sim \mathcal {CN}({\bf{0}}, \tau {{\boldsymbol{I}}}) \quad \quad \quad \quad \quad \ $ | (27) |
| ${{\tilde {\boldsymbol{z}}}}|\tau, {{\rm{H}}_1} \sim \mathcal {CN}({\bf{0}}, {{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}}{{\boldsymbol{R}}_{{{b}}}}{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}^{\rm{H}} + \tau {{\boldsymbol{I}}})$ | (28) |
进一步将目标协方差矩阵重新表示为以下形式[7]:
| ${{{\tilde {\boldsymbol{R}}}}_{{{b}}}} = {({{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}^{\rm{H}}{{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}})^{1/2}}{{\boldsymbol{R}}_{{{b}}}}{({{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}^{\rm{H}}{{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}})^{1/2}} = {{\boldsymbol{VD}}}{{{\boldsymbol{V}}}^{\rm{H}}}$ | (29) |
其中,V是由
| ${{\tilde {\boldsymbol{V}}}} = {{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}}{({{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}^{\rm{H}}{{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}})^{ - 1/2}}{{\boldsymbol{V}}} = [{{{\tilde {\boldsymbol{v}}}}_1}, {{{\tilde {\boldsymbol{v}}}}_2}, \cdots, {{{\tilde {\boldsymbol{v}}}}_r}]$ | (30) |
则
| ${{{\tilde {\boldsymbol{V}}}}^{\bot\rm{H}} }\left[{{\tilde {\boldsymbol{V}}}}{\rm{ }}{{{\tilde {\boldsymbol{V}}}}^ \bot } \right] = \left[{{\bf{0}}_{(N-r) \times r}}{\rm{ }} \ {{{\boldsymbol{I}}}_{(N-r) \times (N-r)}} \right]$ | (31) |
利用上述结论,可以将白化后的协方差矩阵
| $\begin{array}{l} {\mathit{\boldsymbol{\widetilde U}}_S}{\mathit{\boldsymbol{R}}_b}\mathit{\boldsymbol{\widetilde U}}_S^H + \tau \mathit{\boldsymbol{I}}\\ \quad = \left[ {\mathit{\boldsymbol{\widetilde V}}{{\mathit{\boldsymbol{\widetilde V}}}^ \bot }} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}} + \tau {\mathit{\boldsymbol{I}}_r}} & 0\\ 0 & {\tau {\mathit{\boldsymbol{I}}_{N - r}}} \end{array}} \right]{\left[ {\mathit{\boldsymbol{\widetilde V}}\mathit{\boldsymbol{\widetilde V}}{{\mathit{\boldsymbol{\widetilde I}}}^ \bot }} \right]^{\rm{H}}} \end{array}$ | (32) |
其逆矩阵为:
| ${({{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}}{{\mathit{\boldsymbol{R}}}_{{{b}}}}{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}^{\rm{H}} + \tau {{\mathit{\boldsymbol{I}}}})^{ - 1}} = \sum\limits_{i = 1}^r {\frac{1}{{{d_i} + \tau }}{{{\mathit{\boldsymbol{P}}}}\!_{{{{{\tilde {{v}}}}}_i}}}} + \frac{1}{\tau }{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}$ | (33) |
其中,
| $\det {({{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}}{{\boldsymbol{R}}_{{{b}}}}{{\tilde {\mathit{\boldsymbol{U}}}}}_{\rm{S}}^{\rm{H}} + \tau {{\boldsymbol{I}}})^{ - 1}} = {\left( {\frac{1}{\tau }} \right)^{N - r}}\prod\limits_{i = 1}^r {\frac{1}{{{d_i} + \tau }}} $ | (34) |
利用上述矩阵求逆结果,可以将GLRT重新表示为:
| $\frac{\mathop {\max }\limits_D \mathop {\max }\limits_\widetilde{\mathit{\boldsymbol{V}}} \mathop {\max }\limits_\tau {{f}_{1}}(\widetilde{\mathit{\boldsymbol{z}}}|\tau ,\mathit{\boldsymbol{D}},\widetilde{\mathit{\boldsymbol{V}}},{{\rm{H}}_{1}})}{\mathop {\max }\limits_\tau {{f}_{0}}(\widetilde{\mathit{\boldsymbol{z}}}|\tau ,{{\rm{H}}_{0}})}\underset{{{\rm{H}}_{0}}}{\overset{{{\rm{H}}_{\rm{1}}}}{\mathop{\begin{align} & > \\ & < \\ \end{align}}}}\,G$ | (35) |
在H0和H1假设下,对数似然函数分别为:
| ${l_0} = \ln {f_0} \propto - N{\rm ln}\tau - \frac{{{{{{\tilde {\boldsymbol{z}}}}}^{\rm{H}}}{{\tilde {\boldsymbol{z}}}}}}{\tau } \quad \quad \quad \quad \quad \quad $ | (36) |
| $\begin{aligned} {l_1} = & \ln {f_1} {\rm{ }} \propto - (N - r){\rm ln}\tau - \sum\limits_{i = 1}^r {\ln ({d_i} + \tau )} \\ & {\rm{ }} - \sum\limits_{i = 1}^r {\frac{1}{{{d_i} + \tau }}{{{{\tilde {\boldsymbol{z}}}}}^{\rm{H}}}{{{\boldsymbol{P}}}\!_{{{{{\tilde {{v}}}}}_i}}}{{\tilde {\mathit{\boldsymbol{z}}}}}} - \frac{1}{\tau }{{{{\tilde {\boldsymbol{z}}}}}^{\rm{H}}}{{{\boldsymbol{P}}}\!\!_{{{{{\tilde {\boldsymbol{V}}}}}^ \bot }}}{{\tilde {\boldsymbol{z}}}} \end{aligned}$ | (37) |
采用ML方法估计
| ${\hat d_i} + \tau = {{{\tilde {\mathit{\boldsymbol{z}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!_{{{{{\tilde {\mathit{\boldsymbol{v}}}}}}_i}}}{{\tilde {\mathit{\boldsymbol{z}}}}}$ | (38) |
代入
| ${l_1} \propto - N{\rm ln}\tau - \sum\limits_{i = 1}^r {\ln \left( {\frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}_{{{{{\tilde {\mathit{\boldsymbol{v}}}}}}_i}}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}{\tau }} \right)} - \frac{1}{\tau }{{{\tilde {\mathit{\boldsymbol{z}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}}$ | (39) |
进一步在两种假设下计算τ的MAP估计,即
| ${\hat \tau _i} = \mathop {\arg \max }\limits_\tau {f\!_i}(\tau |{{\tilde {\mathit{\boldsymbol{z}}}}}, {{\rm{H}}_i})$ | (40) |
其中,后验PDF
| ${f\!_i}(\tau |{{\tilde {\mathit{\boldsymbol{z}}}}}, {{\rm{H}}_i}) \propto {f\!_i}({{\tilde {\mathit{\boldsymbol{z}}}}}|\tau, {{\rm{H}}_i})p(\tau )$ | (41) |
在H0假设下,将
| ${f_0}(\tau |{{\tilde {\mathit{\boldsymbol{z}}}}}, {{\rm{H}}_0}) \propto {\tau ^{ - (v + 1 + N)}}\exp \left( { - \frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }}{\tau }} \right)$ | (42) |
令
| $\ln {f\!_0}(\tau |{{\tilde {\mathit{\boldsymbol{z}}}}}, {{\rm{H}}_0}) \propto - \zeta \ln \tau - \frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }}{\tau }$ | (43) |
关于τ求偏导,并令偏导等于零,得到τ的MAP估计为:
| $\hat \tau _0^{{\rm{MAP}}} = \frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }}{\zeta }$ | (44) |
将估计值代入式(36),得
| ${l_0} \propto - N{\rm ln}\left( {\frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }}{\zeta }} \right) - \zeta \frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }}$ | (45) |
在H1假设下,令
| $\begin{aligned} {l_1} \propto & - N{\rm ln}\left( {{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta } \right) - \sum\limits_{i = 1}^r {\ln \left( {\varsigma \frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!_{{{{{\tilde {{v}}}}}_i}}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}} \right)} \\ & {\rm{ + ln}}\left( {\frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }}{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}} \right) - \varsigma \frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}} + \beta }} \end{aligned}$ | (46) |
令
| $\mathop {\min }\limits_{{h_i}} \sum\limits_{i = 1}^r {\ln (\varsigma {h_i})} = \ln \left[{\varsigma \left( {\frac{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{\tilde {\mathit{\boldsymbol{V}}}}}}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}{{{{{{\tilde {\mathit{\boldsymbol{z}}}}}}^{\rm{H}}}{{{\mathit{\boldsymbol{P}}}}\!\!_{{{{{\tilde {\mathit{\boldsymbol{V}}}}}}^ \bot }}}{{\tilde {\mathit{\boldsymbol{z}}}}}}}-\frac{{r-1}}{{N-r}}} \right)} \right]$ | (47) |
利用上述推导结果,可以将GLRT最终表示为:
| $\begin{align} & N\ln \left( 1+\frac{{{g}_{0}}-{{g}_{1}}}{{{g}_{1}}+\beta } \right)\text{+ln}\left( \frac{{{g}_{1}}+\beta }{{{g}_{1}}} \right)-\varsigma \frac{{{g}_{1}}}{{{g}_{1}}+\beta } \\ & +\zeta \frac{{{g}_{0}}}{{{g}_{0}}+\beta }-\ln \left[ \varsigma \left( \frac{{{g}_{0}}}{{{g}_{1}}}-\frac{N-1}{N-r} \right) \right]\underset{{{\text{H}}_{0}}}{\overset{{{\text{H}}_{\text{1}}}}{\mathop{\begin{align} & > \\ & < \\ \end{align}}}}\,G \\ \end{align}$ | (48) |
这即为SOG目标的GLRT检验统计量,在后续仿真时将其称之为SOG-GLRT。从检测器结构来看,SOG-GLRT的运算复杂度较FOG-GLRT明显增加。
3.4 协方差矩阵估计方法分别将采样协方差矩阵(Sample Covariance Matrix, SCM)、归一化采样协方差矩阵(Normalized SCM, NSCM)和定点估计(Fixed Point Estimator, FPE)[17]作为协方差矩阵估计值,代入GLRT,即可构造出新的自适应检测器。SCM是较为简单且常用的估计方法,表示为:
| ${{{\bf \hat {\mathit{\boldsymbol{M}}}}}_{{\rm{SCM}}}} = \frac{1}{K}\sum\limits_{k = 1}^K {{{\mathit{\boldsymbol{z}}}_k}{\mathit{\boldsymbol{z}}}_k^{\rm{H}}} $ | (49) |
NSCM可视为归一化形式的SCM,表示为:
| ${\mathit{\boldsymbol{\hat M}}_{{\rm{NSCM}}}} = \frac{1}{K}\sum\limits_{k = 1}^K {\frac{{{\mathit{\boldsymbol{z}}_k}\mathit{\boldsymbol{z}}_k^{\rm{H}}}}{{\mathit{\boldsymbol{z}}_k^{\rm{H}}{\mathit{\boldsymbol{z}}_k}/N}}} = \frac{N}{K}\sum\limits_{k = 1}^K {\frac{{{\mathit{\boldsymbol{z}}_k}\mathit{\boldsymbol{z}}_k^{\rm{H}}}}{{\mathit{\boldsymbol{z}}_k^{\rm{H}}{\mathit{\boldsymbol{z}}_k}}}} $ | (50) |
其中,
| ${{\bf \hat {\mathit{\boldsymbol{M}}}}}_{{\rm{FPE}}}^{}(i + 1) = \frac{1}{K}\sum\limits_{k = 1}^K {\frac{{{{\mathit{\boldsymbol{z}}}_k}{\mathit{\boldsymbol{z}}}_k^{\rm{H}}}}{{\hat \tau (i + 1)}}} $ | (51) |
| $\hat \tau (i + 1) = \frac{{{\mathit{\boldsymbol{z}}}_k^{\rm{H}}{{\bf \hat {\mathit{\boldsymbol{M}}}}}_{{\rm{FPE}}}^{ - 1}(i){{\mathit{\boldsymbol{z}}}_k}}}{N} \quad \quad $ | (52) |
其中,
采用Monte Carlo仿真方法,对本文自适应检测方法的性能进行验证分析。为减小运算量,虚警概率
假定海杂波功率水平为单位值,散斑分量建模为复高斯模型,其协方差矩阵M的第(i, j)个元素为:
| ${[{{\mathit{\boldsymbol{M}}}}]_{i, j}} = {\rho ^{|i - j|}}$ | (53) |
其中,ρ表示1阶相关系数。在后续仿真时,如无特殊说明,纹理分量的形状参数和1阶相关系数分别取v=1.7和ρ=0.9。
在仿真时分别考虑FOG和SOG两类子空间目标。对于前者,假定目标子空间的维数为r=2,导向矩阵E完全已知,归一化多普勒频率分别为fD=0.2和fD=0.3,目标回波功率在子空间各维上均匀分布,且目标幅度矢量a中的各元素均设定为单位值。对于后者,假定目标信号为直升机主旋翼调制信号,表示为
| ${[{{\mathit{\boldsymbol{M}}}_{\rm{S}}}]_{k, l}} = \frac{{{{\sin }^2}[\pi {B_{\rm{S}}}(k-l)]}}{{{{[\pi {B_{\rm{S}}}(k-l)]}^2}}}\exp [-{\rm j}2\pi {f_{\rm{S}}}(k-l)]$ | (54) |
其中,fS和BS分别表示目标信号的归一化多普勒频率和归一化带宽,在仿真时分别取fS=0.3和BS=0.2。
4.1 检测性能对比分析假定协方差矩阵已知,相干脉冲数为N=8,对两类子空间目标的检测性能进行对比分析。分别取v=1.7和v=1.1,则FOG-GLRT和SOG-GLRT的检测性能曲线如图 1(a),图 1(b)所示。由仿真结果可知,当海杂波较为尖锐,即形状参数较小时,两类检测器的性能差异较大,其中,FOG-GLRT的检测性能明显优于SOG-GLRT。逐渐增大形状参数并开展类似分析,当形状参数增大到1.7时,两类检测器的检测性能曲线几乎重叠。由于后续大部分仿真中形状参数均设定为v=1.7,因此在分析时不再给出SOG-GLRT的仿真结果曲线。在两类目标模型假定下,FOG-GLRT的检测性能均随海杂波形状参数的减小而提升,而对于SOG-GLRT,当形状参数减小时其检测性能曲线出现交叉点,对应的SCR分别在0 dB和6 dB附近。
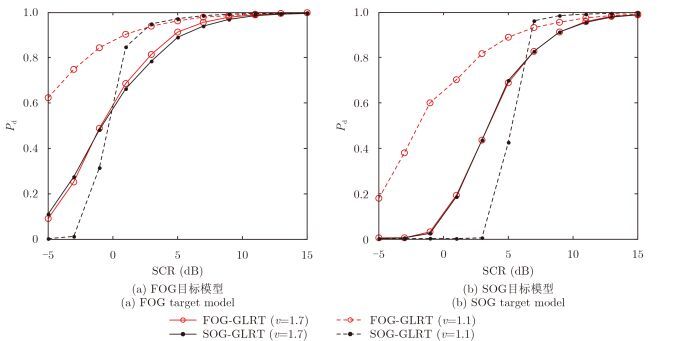
|
图 1 检测性能对比 Fig.1 Comparison of detection performance |
假定参考单元数为K=16,形状参数为v=1.7,不同距离单元之间的纹理分量完全独立。对于3.4节给出的3种协方差矩阵估计方法,自适应FOG-GLRT的性能曲线如图 2所示。可以看出,采用SCM作为协方差矩阵估计值的自适应检测器具有较差的检测性能,相比之下,FPE对应的检测性能较好,但是检测性能的提升是以牺牲检测器的运算复杂度为代价的。而对于NSCM,其运算复杂度和检测性能均介于SCM和FPE之间。当SCR为10 dB时,与NSCM相比,采用FPE作为协方差矩阵估计值的自适应检测器在同等条件下可使检测性能提升21%。
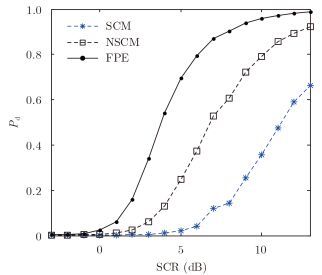
|
图 2 协方差矩阵估计方法的影响 Fig.2 Influence of covariance matrix estimation method |
在分析参考单元数的影响时,取N=8, K为变量(K=8, 16, 32, 64),协方差矩阵估计方法采用NSCM。对于不同的K,仿真结果如图 3所示。由图可知,当参考单元数不足时即K=8的情况,自适应检测器的检测概率几乎为零,此时可认为检测器失效。随着K的增加,检测性能逐步改善,但是改善程度也在逐步收敛,例如,当SCR为10 dB时,采用32个参考单元的自适应检测器与16个参考单元的情况相比,检测性能提升了8.76%,而采用64个参考单元的自适应检测器与32个参考单元的情况相比,检测性能仅提升1.2%。因此,在不改变检测器结构的情况下,通过采用更多参考单元数来实现检测性能提升存在一定的局限性。此外,在高分辨率、高海况等条件下,海杂波通常表现出较强的空间非均匀性,导致有效参考单元数通常不足,在该情况下如何有效改善检测性能,是需要进一步研究的理论问题。
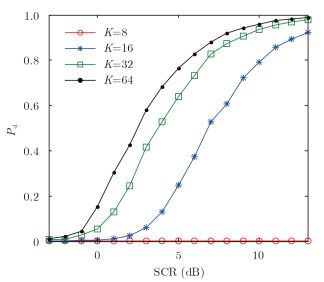
|
图 3 参考单元数的影响 Fig.3 Influence of reference cell numbers |
在4.1节中已初步给出了不同形状参数影响下的检测性能曲线,这里进一步以FOG-GLRT为研究对象分析形状参数的影响。分别取N=8和K=16,形状参数v为变量,当v的取值从v=10.0逐步减小到v=1.1时,仿真结果如图 4(a)所示。由图可知,随着海杂波非高斯程度的增强,检测性能逐渐改善,这主要是因为检测器设计时所考虑的海杂波背景为非高斯模型,非高斯程度越显著,则检测器与背景的匹配程度越好,因此能够取得较好的检测性能。随v的增加,检测性能曲线逐渐收敛,检测概率不再进一步降低。在图 4(b)中,进一步给出了形状参数取极端值时即形状参数无穷大,此时海杂波模型退化为高斯模型自适应检测器的检测性能曲线,未知的协方差矩阵从32个邻近参考单元中估计得到。此外,为便于比较在图中还同时给出了AMF和ANMF的检测性能曲线。可以看出,在高斯背景下,FOG-GLRT与AMF的检测性能一致,且两者均优于ANMF检测器。
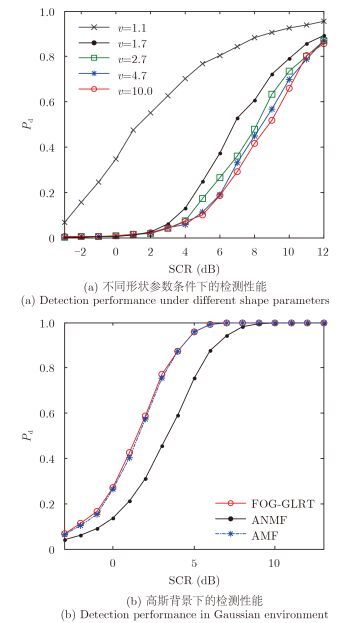
|
图 4 形状参数的影响 Fig.4 Influence of shape parameter |
在上述仿真中,均假定不同距离单元之间的纹理分量为完全独立的情况。这里考虑另一种极端情况,即纹理分量在不同距离单元之间完全相关[27]。实测海杂波中的检测性能将介于这两种极端情况之间。
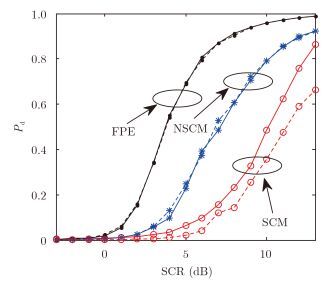
分别考虑3种协方差矩阵估计方法,自适应FOG-GLRT的检测性能曲线如图 5所示,图中的实线和虚线分别对应纹理分量完全相关和完全独立情况。可以看出,对于采用FPE和NSCM作为协方差矩阵估计方法的自适应检测器,其检测性能与纹理分量的空间相关性无关,这与文献[5]给出的检测性能分析结果一致该文关注的是秩1目标,而对于SCM,在纹理分量完全相关的情况下,其检测性能较好。
|
图 5 空间相关性的影响 Fig.5 Influence of spatial correlation |
在仿真分析的基础上,进一步采用某S波段相干雷达海杂波测量数据对检测性能进行验证分析。试验雷达为VV极化,AD采样率为10 MHz,海况约为3-4级,雷达天线工作在驻留模式。在算法验证时,分别取K=32和N=8,并同时根据目标模型和SCR的不同在数据中叠加仿真目标。目标信号建模为直升机主旋翼调制信号,参数同上节的仿真分析一致,SCR定义为:
| ${\rm{SCR}} = \sigma _{\rm{S}}^2/\sigma _{\rm{C}}^2$ | (55) |
其中,
| $\sigma _{\rm{C}}^2 = \frac{1}{{K{N_T}}}\sum\limits_{k = 1}^K {\sum\limits_{n = 1}^{{N_T}} {{c_k}(n)} }$ | (56) |
其中,NT表示单个距离单元包含的总脉冲数,在分析时将虚警概率设定为
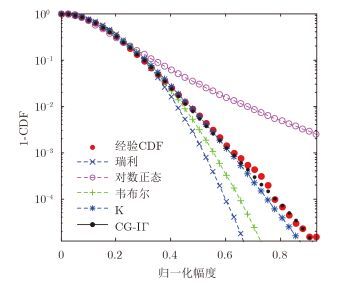
首先对海杂波的统计分布特性进行分析,所采用的理论分布模型包括瑞利、对数正态、韦布尔、K和
|
图 6 海杂波幅度分布建模结果 Fig.6 Amplitude distribution modeling results of sea clutter |
由建模结果可知,海杂波幅度分布明显偏离瑞利模型,与韦布尔和对数正态模型相比,复合高斯模型中的K和CG-
进一步对自适应检测器的检测性能进行定量分析。由于CG-
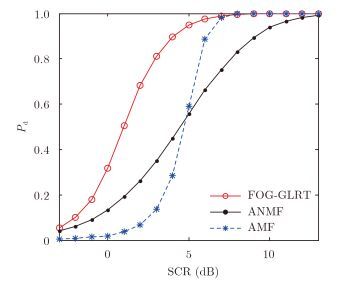
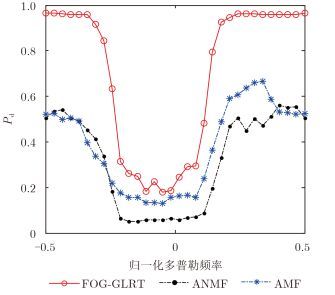
在不同SCR条件下,各检测器在实测海杂波中的检测性能曲线分别如图 7所示。可以看出,在3类检测器中,由于FOG-GLRT在设计阶段考虑了海杂波的幅度分布先验信息,且在检测阶段采用了与当前海杂波环境相匹配的模型参数,因此在检测性能上优于AMF和ANMF检测器。此外,AMF检测器的门限效应较为显著,即,当SCR提升时,其检测性能从几乎检测不到快速变化为几乎完全检测到,在秩1目标模型假设下也可观测到类似结果[17]。在图 8中进一步给出了SCR为5 dB条件下,检测概率随目标信号归一化多普勒频率fS之间的关系曲线。由图可知,在主杂波区,各检测器均形成凹口,凹口最深处对应海杂波的多普勒中心频率,当偏离主杂波区时,各检测器的检测性能均得到改善。从总体上看,本文提出的自适应FOG-GLRT在各频点上的检测性能均优于已有AMF和ANMF检测器。
|
图 7 实测海杂波中的检测性能 Fig.7 Detection performance in measured sea clutter |
|
图 8 检测性能随目标多普勒频率的变化曲线 Fig.8 Variation of detection performance with the target's Doppler frequency |
研究了
| [1] |
何友, 黄勇, 关键, 等. 海杂波中的雷达目标检测技术综述[J].
现代雷达, 2014, 36(12): 1-9. He Y, Huang Y, Guan J, et al..An overview on radar target detection in sea clutter[J]. Modern Radar, 2014, 36(12): 1-9.DOI:10.3969/j.issn.1004-7859.2014.12.001(  0) 0)
|
| [2] |
Ward K, Tough R, and Watts S. Sea Clutter: Scattering, the K-Distribution and Radar Performance, 2nd ed[M]. London: The Institution of Engineering and Technology, 2013.
( 0) 0)
|
| [3] |
Gini F and Farina A. Vector subspace detection in compound-Gaussian clutter, Part Ⅰ: Surgey and new results[J].
IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4): 1295-1311.DOI:10.1109/TAES.2002.1145751( 0) 0)
|
| [4] |
Conte E, Lops M and and Ricci G. Asymptotically optimum radar detection in compound-Gaussian clutter[J].
IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 617-625.DOI:10.1109/7.381910( 0) 0)
|
| [5] |
Gini F. Suboptimum coherent radar detection in a mixture of K-distributed and Gaussian clutter[J].
IEE Proceedings, Radar, Sonar and Navigation, 1997, 144(1): 39-48.DOI:10.1049/ip-rsn:19970967( 0) 0)
|
| [6] |
Jin Y and Friedlander B. A CFAR adaptive subspace detector for second-order Gaussian signals[J].
IEEE Transactions on Signal Processing, 2005, 53(3): 871-884.DOI:10.1109/TSP.2004.842196( 0) 0)
|
| [7] |
Bon N, Khenchaf A and and Garello R. GLRT subspace detection for range and Doppler distributed targets[J].
IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 678-696.DOI:10.1109/TAES.2008.4560214( 0) 0)
|
| [8] |
Liu J, Zhang Z J, Yang Y, et al..A CFAR adaptive subspace detector for first-order or second-order Gaussian signals based on a single observation[J].
IEEE Transactions on Signal Processing, 2011, 59(11): 5126-5140.DOI:10.1109/TSP.2011.2164073( 0) 0)
|
| [9] |
Robey F C, Fuhrman D L, Kelly E J, et al..A CFAR adaptive matched filter detector[J].
IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208-216.DOI:10.1109/7.135446( 0) 0)
|
| [10] |
Kraut S, Scharf L L and and McWhorter L T. Adaptive subspace detectors[J].
IEEE Transactions on Signal Processing, 2001, 49(1): 1-16.DOI:10.1109/78.890324( 0) 0)
|
| [11] |
Kraut S and Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J].
IEEE Transactions on Signal Processing, 1999, 47(9): 2538-2541.DOI:10.1109/78.782198( 0) 0)
|
| [12] |
Liu W J, Xie W C, Liu J, et al..Adaptive double subspace signal detection in Gaussian background—Part Ⅰ: Homogeneous environments[J].
IEEE Transactions on Signal Processing, 2014, 62(9): 2345-2357.DOI:10.1109/TSP.2014.2309556( 0) 0)
|
| [13] |
Liu W J, Xie W C, Liu J, et al..Adaptive double subspace signal detection in Gaussian background—Part Ⅱ: Partially homogeneous environments[J].
IEEE Transactions on Signal Processing, 2014, 62(9): 2358-2369.DOI:10.1109/TSP.2014.2309553( 0) 0)
|
| [14] |
丁昊, 薛永华, 黄勇, 等. 均匀和部分均匀杂波中子空间目标的斜对称自适应检测方法[J].
雷达学报, 2015, 4(4): 418-430. Ding H, Xue Y H, Huang Y, et al..Persymmetric adaptive detectors of subspace signals in homogeneous and partially homogeneous clutter[J]. Jounal of Radars, 2015, 4(4): 418-430.(  0) 0)
|
| [15] |
JIAN T, HE Y, LIAO G S, et al..Adaptive persymmetric detector of generalised likelihood ratio test in homogeneous environment[J].
IET Signal Processing, 2016, 10(2): 91-99.DOI:10.1049/iet-spr.2015.0200( 0) 0)
|
| [16] |
Conte E, Lops M and and Ricci G. Adaptive matched filter detection in spherically invariant noise[J].
IEEE Signal Processing Letters, 1996, 3(8): 248-250.DOI:10.1109/97.511809( 0) 0)
|
| [17] |
Conte E and Maio A D. Mitigation techniques for non-Gaussian sea clutter[J].
IEEE Journal of Ocean Engineering, 2004, 29(2): 284-302.DOI:10.1109/JOE.2004.826901( 0) 0)
|
| [18] |
Gao Y C, Liao G S and and Liu W J. High resolution radar detection in interference and non-homogeneous noise[J].
IEEE Signal Processing Letters, 2016DOI:10.1109/LSP.2016.2597738( 0) 0)
|
| [19] |
刘明, 水鹏朗. 海杂波背景下的组合自适应GLRT-LTD[J].
电子与信息学报, 2015, 37(12): 2834-2990. Liu M and Shui Shui. Combined adaptive GLRT-LTD against sea clutter[J]. Journal of Electronics & Information Technology, 2015, 37(12): 2834-2990.(  0) 0)
|
| [20] |
GAO Y C, LIAO G S, ZHU S Q, et al..A persymmetric GLRT for adaptive detection in compound-Gaussian clutter with random texture[J].
IEEE Signal Processing Letters, 2013, 20(6): 615-618.DOI:10.1109/LSP.2013.2259232( 0) 0)
|
| [21] |
Kong L J, Li N, Cui G L, et al..Adaptive Bayesian detection for multiple-input multiple-output radar in compound-Gaussian clutter with random texture[J].
IET Radar, Sonar & Navigation, 2016, 10(4): 689-698.( 0) 0)
|
| [22] |
Balleri A, Nehorai A and and Wang J. Maximum likelihood estimation for compound-Gaussian clutter with inverse Gamma texture[J].
IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 775-780.DOI:10.1109/TAES.2007.4285370( 0) 0)
|
| [23] |
Bandiera F, Besson O and and Ricci G. Knowledge-aided covariance matrix estimation and adaptive detection in compound-Gaussian noise[J].
IEEE Transactions on Signal Processing, 2010, 58(10): 5391-5396.DOI:10.1109/TSP.2010.2052922( 0) 0)
|
| [24] |
Sangston K J, Gini F and and Greco M S. Coherent radar target detection in heavy-tailed compound-Gaussian clutter[J].
IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 64-77.DOI:10.1109/TAES.2012.6129621( 0) 0)
|
| [25] |
Ding H, Guan J, Liu N B, et al..New spatial correlation models for sea clutter[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(9): 1833-1837.DOI:10.1109/LGRS.2015.2430371( 0) 0)
|
| [26] |
Gini F and Farina A. Matched subspace CFAR detection of hovering helicopters[J].
IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1293-1305.DOI:10.1109/7.805446( 0) 0)
|
| [27] |
Pulsone N B and Raghavan R S. Analysis of an adaptive CFAR detector in non-Gaussian interference[J].
IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 903-916.DOI:10.1109/7.784060( 0) 0)
|
| [28] |
Chan H C. Radar sea-clutter at low grazing angles[J].
IEE Proceedings-F, 1990, 137(2): 102-112.( 0) 0)
|




