1 引言

合成孔径雷达 (Synthetic Aperture Radar, SAR) 图像特征提取是SAR目标识别中的关键步骤。如何提取区分性强且能反映SAR图像电磁散射机理的特征能够有效提高SAR目标识别的性能。理论和实验表明，在高频区目标总的电磁散射可以看成由有限个局部散射源叠加而成，这些局部散射源称为散射中心^[1]。为了有效地表征散射中心的电磁散射特性，研究人员相继提出了点散射中心模型、GTD模型^[2]、属性散射中心模型^[3]。属性散射中心由于赋予了散射中心与其物理属性相关的属性参数而成为SAR目标识别的研究热点。

基于散射中心的识别方法按照其实施策略可以分为两类。第1类方法通过构建散射中心的对应关系进而在此匹配关系的基础上评价散射中心的相似性。Randolph L.Mose提出了一种散射中心匹配的Beyesian方法，通过最大后验的方法实现目标类别判断^[4]。文献[5]提取散射中心的KL (Karhunen-Loeve) 特征构建匹配矩阵，采用最近邻和门限判决相结合的方法序贯匹配散射中心特征。文献[6]基于World View Vector (WVV) 构造具有仿射不变性的散射中心特征并采用Hopcroft_Karp (HK) 算法实现散射中心的匹配。另一类方法则回避了较为复杂的散射中心匹配过程，直接评价点集的相似度。Bhanu采用隐马尔科夫模型对散射中心建模并应用于目标识别^[7]。Dungan分别采用了Least Square Trimmed HausDorff距离 (LST-HD)^[8]和Pyramid Match Kernel (PMK)^[9]评价散射中心特征的相似度。文献[10]采用点-区域匹配的策略替代点模式匹配的方法。相比第1类方法，第2类方法在减少复杂度的同时牺牲了一定的识别精度和稳健性。

有效建立散射中心的匹配关系不仅有助于解决扩展操作条件 (Extended Operating Condition, EOC) 如目标部分缺失、被遮挡等情形下的目标识别问题，还能够以更为直观的方式辅助人工解译。探索和解决这一问题对于SAR目标识别具有十分重要的意义。文献[10]分析了建立散射中心匹配关系中存在的难点问题：(1) 存在冗余的散射中心，包括散射中心的缺失和虚假散射中心；(2) 由于噪声导致的散射中心提取误差；(3) 姿态角估计误差导致的散射中心失配。本文统筹考虑上述3点难点问题，提出了一种散射中心匹配方法并将其应用于SAR目标识别。该方法首先基于属性散射中心模型提取待测试SAR图像的属性散射中心以及模板的属性散射中心，通过散射中心的属性差异构建合理的代价矩阵进而采用Hungarian算法^[11]实现实测散射中心与模板散射中心的匹配。代价矩阵的构建过程中考虑了散射中心漏警和虚警的代价；Hungarian算法是一种联合优化算法，对于散射中心的提取误差具有一定的抗干扰性。在此匹配关系的基础上，本文设计一种稳健的散射中心匹配度度量准则，该准则综合考虑了不同散射中心对于匹配度的贡献以及散射中心虚警和漏警对于最终匹配度的影响。为了解决由于姿态角估计引入的误差，本文在估计姿态角的邻域选择多个模板，通过多个模板的综合计算得到更为准确的匹配度。基于Moving and Stationary Target Acquisition and Recognition (MSTAR) 数据集的实验验证了提出方法的有效性。

2 目标属性散射中心提取

属性散射中心模型^[3]是Moses Randolph L等人基于几何绕射理论和物理光学理论提出的描述高频区复杂目标散射特性的参数模型，目标的电磁散射响应可以认为是p个独立的散射中心叠加而成，具体形式如下：

$E(f, \phi ;\mathit{\Theta }) = \sum\limits_{i = 1}^p {{E_i}(f, \phi ;{{{\theta }}_i})}$

(1)

$\begin{aligned} {E_i}(f, \phi ;{{{\theta }}_i}) =&{A_i} \cdot {\left({\rm j}\frac{f}{{{f\!_c}}}\right)^{{\alpha _i}}}\\ & \cdot \exp \left( {\frac{{ - {\rm j}4\pi f}}{c}({x_i}\cos \phi + {y_i}\sin \phi )} \right)\\ & \cdot {\rm{sinc}}\left( {\frac{{2\pi f}}{c}{L_i}\sin (\phi - {{\bar \phi }_i})} \right)\\ & \cdot \exp ( - 2\pi f{\gamma _i}\sin \phi ) \end{aligned}$

(2)

式中，$E(f, \phi ;\mathit{\Theta })$为目标总的散射场，其中$\mathit{\Theta } = \{ {{{\theta }}_i}\} = $$[{A_i}, {\alpha _i}, {x_i}, {y_i}, {L_i}, {{\bar \phi }_i}, {\gamma _i}]$为散射中心的属性集。${x_i}, {y_i}$分别表示散射中心方位向、距离向的位置，A_i表示幅度，${\alpha _i}$是频率依赖因子，L_i是散射中心长度，${{\bar \phi }_i} $是散射中心方向角，${\gamma _i}$表示散射中心对方向角$\phi $的方向依赖性。当${L_i} = {{\bar \phi }_i} = 0$时，表示该散射中心是局部散射中心，当${L_i} \ne 0, {\gamma _i} = 0$时，表示该散射中心是分布式散射中心。

本文采用文献[3]中提出的AML算法进行散射中心参数估计。对于SAR频域观测数据D$(f, \phi )$，散射中心模型的参数估计问题可以写成如式 (3) 形式。其中，D$(f, \phi )$代表观测项 (SAR回波)，$E(f, \phi ;\mathit{\Theta })$代表模型项，$N(f, \phi )$表示噪声干扰以及模型失配带来的误差。

$D(f, \phi ) = E(f, \phi ;\mathit{\Theta }) + N(f, \phi )$

(3)

则极大似然参数估计为：

${\mathit{\Theta }_{\rm ML}} = \arg \mathop {\min }\limits_\mathit{\Theta } {\Large||} D - E(\mathit{\Theta }){\Large||}{^2}$

(4)

AML算法的主要步骤如下：

步骤1  采用分水岭算法^[12]分割SAR图像的高能量区域；

步骤2  根据分割区域初始化散射中心参数，利用优化算法 (如牛顿迭代法^[13]) 搜寻最佳参数；

步骤3  根据估计参数重构散射中心并采用CLEAN算法^[14]将重构散射中心从目标区域剔除；

步骤4  重复步骤1到步骤3估计下一个散射中心直到残差达到下限或者散射中心数目达到上限。

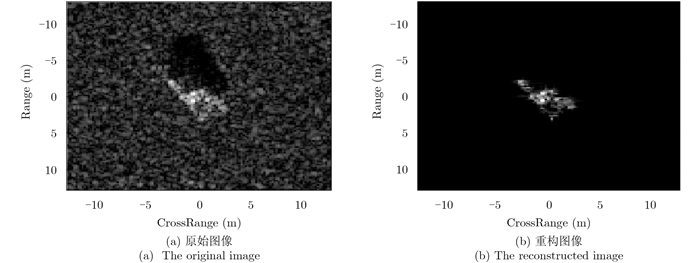
采用AML算法对一幅BMP2 SAR图像进行参数估计并进行目标重构，结果如图 1所示。本文选用了[A, x, y, L]作为散射中心特征进行散射中心匹配，因为这些特征直接与目标的物理结构相关从而有助于提高目标识别性能。由于频率依赖因子α难以得到较好的估计，本文并没有选用其作为待匹配的特征。特别地，对于分布式散射中心，考虑到雷达倾角较大时分布式散射中心会分裂为位于其两端的两个尖峰^[15]，本文统一用其两个端点作为局部式散射中心对其予以表达。由于不同SAR图像存在辐射强度差异，本文对幅度因子做了归一化处理，最终每个散射中心的属性参数即为[A, x, y]。

3 散射中心的匹配

本文采用Hungarian算法实现散射中心的匹配。Hungarian算法是一种联合优化算法并被广泛应用任务分配问题。通过构建分配代价矩阵，Hungarian算法通过二分图的匹配问题找到最佳的分配关系使得总的分配代价最小^[11]。在相同的测量条件下，同类目标的散射中心在理论上具有一一对应的关系，因此Hungarian算法适用于散射中心的匹配。由于实际过程中不可避免地存在背景噪声带来的虚假散射中心 (虚警，False Alarm (FA)) 以及目标缺失的散射中心 (漏警，Missing Alarm (MA))，本文在构建分配代价矩阵时将漏警和虚警综合考虑进来。分别将模板散射中心和测试散射中心记为${\boldsymbol{X}} = [{{\boldsymbol{X}}_1} \;{{\boldsymbol{X}}_2} \;{{\boldsymbol{X}}_3} \; \cdots \;{\rm{ }}{{\boldsymbol{X}}_m}]$以及${\boldsymbol{Y}} =$ $[{{\boldsymbol{Y}}_1} \;{{\boldsymbol{Y}}_2} \;{{\boldsymbol{Y}}_3} \; \cdots \;{{\boldsymbol{Y}}_n}]$。构造的分配代价矩阵如表 1所示。

表 1中

$\begin{array}{l} {C_{ij}} \!=\! [{({X_{ix}}-{Y_{jx}})^2} \!+\! {({X_{iy}} \!-\! {Y_{jy}})^2}] * \exp (|{X_{iA}}\! -\! {Y_{jA}}|), \\ {M_i} = \frac{1}{n}\sum\limits_{j = 1}^n {{C_{ij}}} {\rm{ }}, \;\;{F_i} = \frac{1}{m}\sum\limits_{j = 1}^m {{C_{ji}}} \end{array}$

(5)

设定将X_i配给Y_i的代价为两者强度属性差值对位置属性的欧式距离的加权；将一个模板散射中心分配给漏警的代价为将其分配给所有实测散射中心的平均值；将一个实测散射中心分配给虚警的代价为将其分配给所有模板散射中心的代价的平均值。

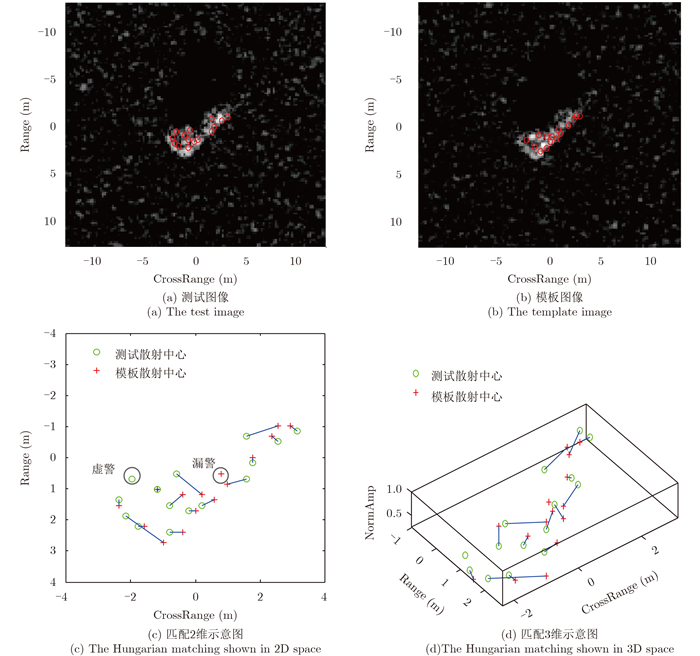
相比最近邻匹配方法，Hungarian匹配存在一个联合优化的过程，因此该方法更具有稳健性。图 2给出了利用Hungarian算法实现散射中心匹配的一个实例。

4 散射中心的匹配度度量 4.1 门限法实现匹配对划分

通过散射中心的Hungarian匹配，每一个模板散射中心分配给某一个测试散射中心或者漏警；同样，每一个测试散射中心匹配了某一模板散射中心或者虚警。本文在此匹配关系的基础上，采用门限法对匹配对进行进一步划分。

由于散射中心提取误差，模板散射中心和测试散射中心均可看作随机变量。文献[4]采用高斯模型对散射中心属性的不确定性进行建模。为了方便起见，假定模板散射中心为确定量，测试散射中心为随机变量。各属性的分布参数如表 2所示。

${x_0}, {y_0}, {A_0}$为测试散射中心的提取属性，CRR代表方位向分辨率，RR指距离向分辨率。假定各个属性相互独立，在给定置信度水平β(如图 3阴影区域所示) 的情况下，可以根据各个属性的分布计算相应的判决门限T_x, T_y, T_A(式 (6))。

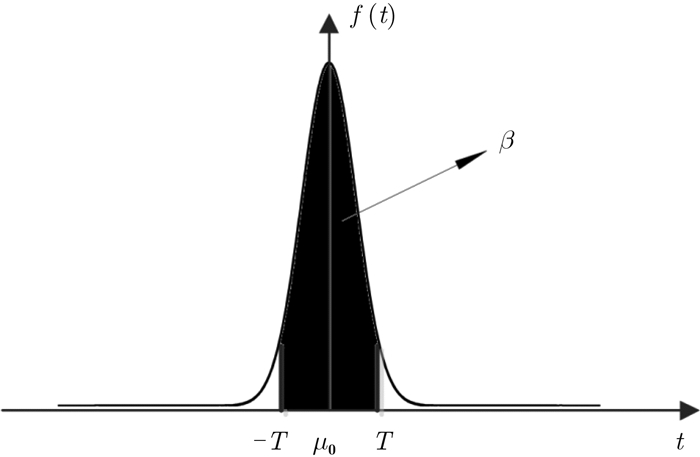
$\int_{ - T}^T {f(t, {\mu _0}, {\delta _0})} {\rm d}t = \beta $

(6)

其中，$f(t, {\mu _0}, {\delta _0})$代表均值为${\mu _0}$方差为${\delta _0}$的高斯分布。在计算门限的基础上，将所有的匹配对化分为“强匹配对”和“弱匹配对”。假定模板散射中心X_i与测试散射中心${{\boldsymbol{Y}}_{\Gamma (i)}}$匹配，其满足“强匹配对”的条件如下：

$\left\{ \begin{array}{l} {\rm{ }}\left| {{X_{ix}} - {Y_{\Gamma (i)x}}} \right| < {T_x}\\ {\rm{ }}\left| {{X_{iy}} - {Y_{\Gamma (i)y}}} \right| < {T_y}\\ {\rm{ }}\left| {{X_{iA}} - {Y_{\Gamma (i)A}}} \right| < {T_A} \end{array} \right.$

(7)

4.2 匹配度计算

如何合理评价模板散射中心与测试散射中心的匹配度是实现目标识别的核心环节。本文在Hungarian匹配以及散射中心匹配对划分的基础上，设计了一种散射中心匹配度计算方法。

假设在Hungarian匹配后，有k个模板散射中心分配给测试散射中心，s个漏警以及q个虚警。进而我们通过门限法选择了l个“强匹配对”。k, s, q, l的关系如式 (8) 所列。

$\left\{ \begin{array}{l} {\rm{ }}2 * k + s + q = m + n\\ {\rm{ }}k \le \min (m, n)\\ {\rm{ }}l \le k \end{array} \right.$

(8)

在评价散射中心匹配度时，本文综合考虑了3个因素。首先，不同的散射中心对于最终匹配度的贡献不同。强散射中心在提取过程中更为稳定且不容易被噪声和邻近散射中心干扰和“淹没”，因此强散射中心更为重要。其次，“强匹配对”比“弱匹配对”更为重要，更多的强匹配对意味着更好的匹配。最后，应当合理评价散射中心漏警和虚警的评价，更多的漏警和虚警将造成低的匹配度。

对于第1个因素，我们根据模板散射中心的幅度计算线性的权重因子：

${P_i} = {{\left| {{A_i}} \right|} \mathord{\left/ {\vphantom {{\left| {{A_i}} \right|} {\sum\limits_{j = 1}^m {\left| {{A_i}} \right|} }}} \right. } {\sum\limits_{j = 1}^m {\left| {{A_i}} \right|} }}$

(9)

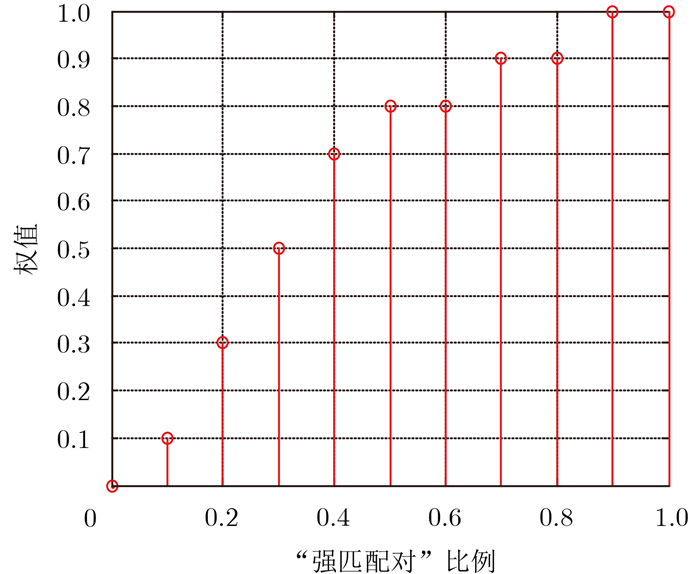
为了评价第2个因素，根据“强匹配对”的比例R(式 (10)) 赋予如图 4所示的离散函数加权：

$R = \frac{l}{{\min (m, n)}}$

(10)

采用二次函数权值评价散射中心虚警和漏警：

${\omega _A} = 1 - {\left(\frac{{s + q}}{{m + n}}\right)^2}$

(11)

考虑到噪声以及提取误差，少量的漏警和虚警不可避免。因此在漏警和虚警较少时权值衰减较慢；当漏警和虚警的数量增多是，权值的衰减将不断加剧。

图 5给出了权值ω_A随漏警和虚警数量变化的示例。例中m+n=30，当不存在漏警和虚警时，权值为1；随着漏警和虚警的数量增多，权值不断下降；当所有的模板散射中心都判为漏警时，权值为0。

根据匹配对的属性差异计算基础匹配度如下：

$\begin{aligned} {\rm{B}}{{\rm{S}}_i} =&\exp \Bigg\{ { - \left[{{{({X_{ix}}-{Y_{\Gamma (i)x}})}^2} + {{({X_{iy}}-{Y_{\Gamma (i)y}})}^2}} \right.} \\ & {{{\left. { + {{({X_{iA}}-{Y_{\Gamma (i)A}})}^{\rm{2}}{\rm{/2}}}} \right]}^{ - 1/2}}} \Bigg\} \end{aligned}$

(12)

加权过的最终匹配度为：

${\rm{Sim}} = {\omega _S} * {\omega _A} * \sum\limits_{i = 1}^k \left({{P_i}} * {\rm{B}}{{\rm{S}}_i}\right)$

(13)

4.3 本文方法的基本流程

图 6给出了本文方法的基本流程，主要包括以下几个步骤：

步骤1  利用AML算法提取测试SAR图像的属性散射中心；估计测试图像的方位角^[16]；

步骤2  根据测试图像的估计方位角在模板库中选取模板SAR图像；提取模板SAR图像的散射中心；

步骤3  测试散射中心和模板散射中心的Hungarian匹配和散射中心匹配度的计算；

步骤4  根据实测图像与不同目标模板的匹配度判断目标类别，具有最大匹配度的模板判为目标类别。

在实际过程中，由于测试图像和模板图像通常观测条件会不同，测试图像的散射中心集合于模板图像散射中心集合会存在一定程度的变形，这给散射中心的匹配带来了一定的困难。为了更好地克服这一因素，本文在一定的平移区间内优化得到稳健的匹配度。假定测试图像和模板图像的平移量在3个像素以内，则按照式 (14) 计算匹配度。

${\rm RS} = \mathop {\arg \max }\limits_{t \in [-3 \ {\rm{pi}}, 3 \ {\rm{pi}}]} G(g(X, t), Y \ )$

(14)

式中，函数s代表平移量，g代表平移函数，函数G按照式 (13) 计算匹配度。考虑到方位角估计的误差，本文以估计方位角为中心，选取其左右各5°的模板作为候选模板图像。某一类目标的最终匹配度为所有该类候选模板匹配度的平均值。

5 实验结果与分析 5.1 目标识别实验

实验数据采用美国MSTAR研究计划公开发布的X波段的实测SAR图像数据中的BMP2, BTR70, T72 3类目标。传感器中心频率为9.6 GHz，带宽0.59 GHz；图像分辨率为0.3 m×0.3 m。以俯仰角17°的图像作为模板图像，俯仰角15°的图像为测试图像，表 3中给出了模板数据集和测试数据集的目标类别和样本个数。

模型定阶是散射中心提取中的一大难点。为了验证本文方法对于模型定阶的稳健性，本文在多个模型阶数下测试了提出方法的识别性能。

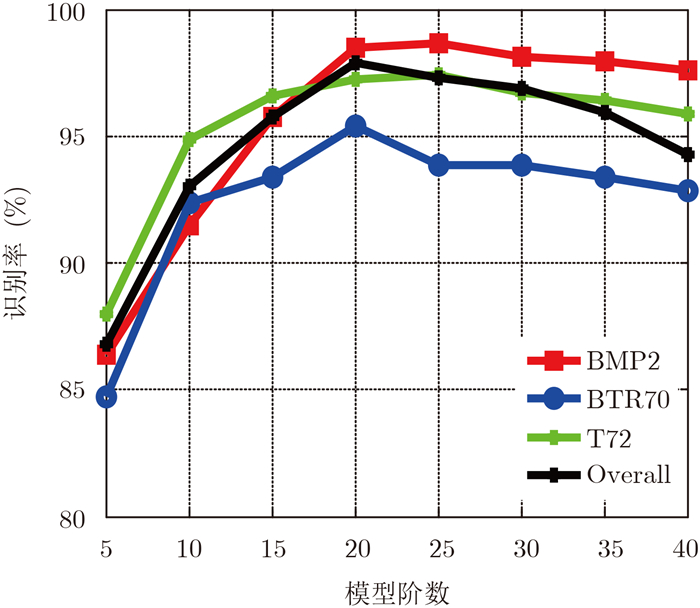
设定置信度水平β=0.9。表 4给出了本文方法在模型阶数N=20时候的识别结果，3类目标的识别率均达到95%以上，平均识别率达到97.88%。图 7给出了方法在不同模型阶数下的3类目标的识别率以及平均识别率。当模型阶数较低时，本文方法的识别率均处于较低的水平，这是因为提取的散射中心较少导致真实存在的散射中心未被有效提取从而导致漏警增加。当模型阶数过大时，本文方法的识别率也出现了一定程度的下降，这是因为提取的虚假散射中心过多从而导致虚警的代价变大。

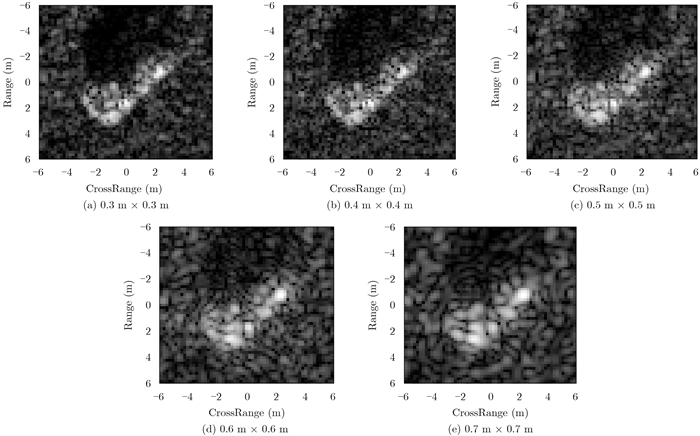
图像分辨率对于散射中心的提取存在一定的影响^[3]。测试本文算法在不同分辨率下的识别性能，通过傅里叶变换将原始的MSTAR图像变换到频域并根据预先设定的分辨率大小截取相应的频域数据构造不同分辨率的图像 (采样率与原始图像保持一致)。图 8给出了一幅MSTAR图像不同分辨率下的结果。

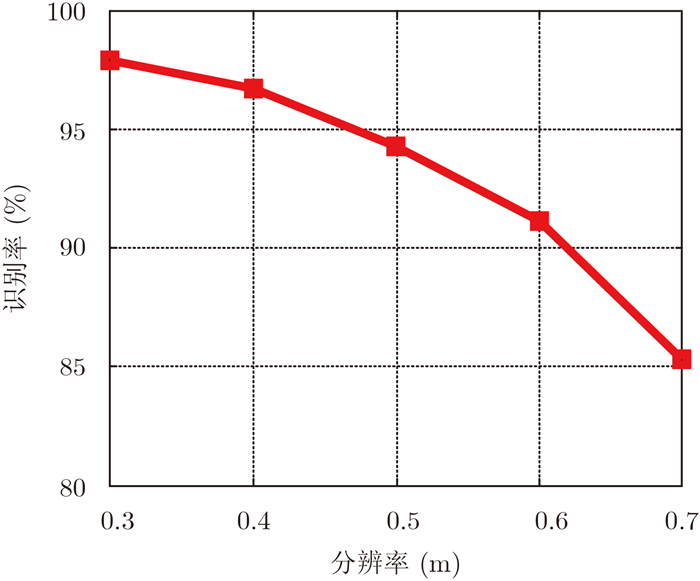
图 9显示本文方法的识别性能随分辨率变化的结果，识别率随着分辨率的降低不断下降。根据表 2中的散射中心属性不确定性建模，随着SAR图像分辨率的下降，散射中心位置属性的不确定性增大 (方差变大)。这将导致单个散射中心匹配代价的评价失准从而导致最终建立的匹配关系存在偏差。

为了测试本文方法对噪声的敏感性，在原始MSTAR图像的频域添加高斯噪声，测试不同信噪比 (Signal to Noise Ratio, SNR) 下的识别性能。为了计算和操作方便，本文假定原始的MSTAR图像无噪声添加，进而根据原始图像的能量添加对应信噪比的高斯噪声，具体的信噪比计算公式如下：

${\rm{SNR}}({\rm{dB}}) = 10\lg {{\displaystyle\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left| {x(i, j)} \right|}^2}} } } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{{\left| {x(i, j)} \right|}^2}} } } {\left( {MN{\sigma ^2}} \right)}}} \right. } {\left( {MN{\sigma ^2}} \right)}}$

(15)

式 (15) 中，M和N分别代表MSTAR图像的长和高，x(i, j) 代表对应的像素值，σ²为高斯噪声的方差。

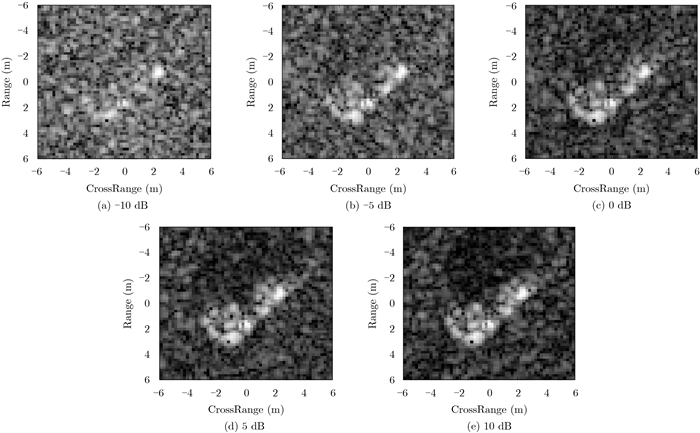
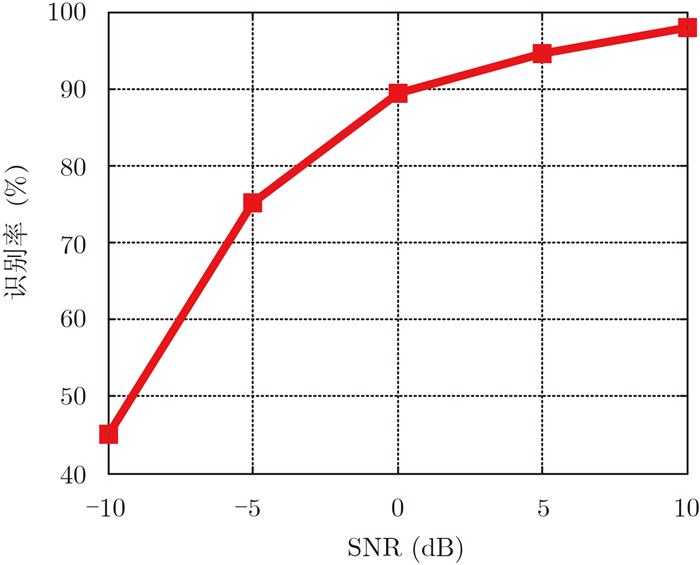
图 10显示了不同信噪比下的MSTAR图像。图 11给出了识别率随信噪比变化的曲线。在信噪比较低时，散射中心被噪声淹没 (如图 10(a)) 或者被严重干扰导致散射中心提取的误差大、虚警漏警增多，识别率处于较低的水平。如式 (3)，式 (4) 所示，属性散射中心的提取实际就是从噪声背景中提取目标特性的过程，随着噪声的增强，通过优化过程 (式 (4)) 提取得到的散射中心属性参数将存在更大的误差。同时，噪声的引入会带来更多的散射中心虚警从而进一步导致目标识别性能的下降。

5.2 方法对比

本文对比了提出算法和基于最近邻LST-HD的识别方法^[8](记为方法一) 以及散射中心序贯匹配方法^[5](记为方法二) 针对3类目标的识别结果。表 5比较了3种方法在模型阶数N=20下的识别性能。本文方法具有最高的识别率。在时间效率上，方法一采用LST-HD衡量散射中心相似度，避免了散射中心的匹配过程，因此识别单幅SAR数据的消耗时间 (不包括散射中心提取时间) 最少，本文方法采用Hungarian算法实现散射中心匹配相比方法二的最近邻匹配方法效率更高。可见，本文提出的算法能够更好地发挥属性散射中心在SAR目标识别中的潜能。

6 结论

基于散射中心特征的SAR目标识别是目前SAR目标识别领域的一大热点。本文提出了一种属性散射中心匹配以及匹配度度量方法并将其应用于SAR目标识别。采用Hungarian算法实现散射中心的匹配，在匹配关系的基础上，设计了一种稳健、全面的匹配度度量方法评价散射中心的匹配度。本文方法在散射中心匹配和匹配度计算的过程中都充分考虑了不同散射中心以及散射中心虚警和漏警对最终匹配度的影响，有助于实现更为稳健的SAR目标识别。采用3类MSTAR目标数据的实验表明，本文方法的平均识别率可以达到97.88%。同时，本文方法对于图像分辨率变化、噪声影响都具有一定的稳健性。与另两种方法的对比实验进一步验证了本文方法的有效性。