1 引言

极化SAR (Synthetic Aperture Radar, SAR)图像地物分类在地质勘探、地形分析以及灾害监测等方面具有广泛的应用^[1]。普通SAR图像由于含有较少的信息，使地物分类精度较低，而多极化SAR图像包含多种极化方式使图像能够获得目标的全部极化散射特性，从而能够取得较好的分类结果^[2,3]。根据分类过程中是否需要加入人为因素的干预，可以将分类过程分为监督分类和无监督分类两大类。一般来说，无监督分类由于缺少先验知识的引导，因此其分类精度相对较低；而监督分类在选取的训练样本具有足够代表性的前提下，可以达到很高的分类精度。极化SAR图像地物分类方法在1988年由麻省理工学院的Jin-Au Kong领导的研究组首次提出，这是极化SAR图像Bayes有监督分类的最初形式^[3,4]。经过20多年的发展，国内外众多学者针对极化SAR数据有监督地物分类提出了很多方法，包括线性(或非线性)判别函数法、支持矢量机、神经网络、Bayes决策等^[5–7]。

近年来，随着获取的极化SAR图像越来越复杂，对地物分类提出了更多的挑战。例如，Bayes决策分类方法需要对极化SAR图像数据进行复杂的统计建模；传统的提取一种或少数几种特征的方式难以表达图像中的目标包含的本质信息^[8,9]。因此，为了得到更高的极化SAR图像地物分类精度，对原有的分类模型进行改进或者提出新的分类模型势在必行。

Lafferty教授^[10]在2001年提出的一种最初应用于文本序列分割和标记的CRF (Conditional Random Fields, CRF)模型引起了分类领域学者的高度重视。Kumar和Hebert^[11]将CRF模型扩展到2维领域，使CRF模型可以使用不同的势函数以满足机器视觉领域的各种具体应用要求，极大地增加了CRF模型的灵活性。CRF模型是一种对标记图像和观测图像直接建模的后验概率模型，可以避免因统计模型不准确而造成的分类精度下降问题。CRF模型不仅能够利用上下文信息，而且有很强的融合多特征的能力，因此对地物类型复杂的极化SAR图像有良好的分类能力。CRF模型对从图像中提取的多种特征的传统利用方法是将任一像素点的全部特征首尾相接而堆叠成一个特征矢量。理论上，提取的极化SAR图像特征越多，分类器的性能越好，得到的极化SAR图像分类精度越高^[8]。但是，特征维度的增加将导致以下两方面的问题：一是多种特征之间存在干扰使得模型在训练时难以获取某些重要特征所表征的目标本质信息^[8]；二是同其它分类器一样，过多的特征可能会导致在训练分类模型时产生过拟合的问题，从而使模型的泛化能力下降。解决上述问题的第1种技术途径是特征稀疏化处理，包括PCA^[8]、l-1正则化法^[8]等特征选择的方法；另一种途径是多分类器组合方法。

本文针对基于堆叠特征的CRF模型容易引起特征干扰和过拟合的问题，提出了一种组合CRF模型用于极化SAR图像的地物分类问题。组合CRF模型首先将不同类型的特征分成多个特征子集合分别训练同一个CRF模型得到多个有差异的子分类器，从而得到多个地物分类结果，然后以单个子分类器的分类精度作为加权系数将多个分类结果进行融合以得到最终的分类结果。两组真实数据的实验结果表明，组合CRF模型相比于传统的特征堆叠利用多特征的方式，其分类精度有明显提高。

2 条件随机场模型

概率图模型是图论和概率论相结合而发展起来的产物，能够描述机器视觉、图像处理领域日益复杂的数据关系^[12]。概率图模型根据变量之间是否存在因果性的依赖关系，可以分为：有向图模型，如Bayes网络^[13]等；无向图模型，如马尔科夫随机场^[14](Markov Random Field, MRF)和CRF^[15]等随机场模型。随机场模型的应用始于对MRF的研究，经过多年的发展，MRF已经成功地应用于图像分析的各个领域。在研究的过程中，MRF的一些劣势限制了其发展，比如MRF需要对输入特征的似然分布进行详细的建模以及对观测到的图像特征集作条件独立假设，而CRF是对后验概率直接建模，不存在这种限制，从而使其在极化SAR图像分类领域获得了广泛的应用^[16]。

2.1 CRF数学描述

Lafferty教授^[10]对条件随机场进行了详细的定义：对于随机场x和y，当给定随机场y时，x的分布满足马尔科夫性质^[8]：

$p({x_i}|{{y}},{x_j},j \ne i,j \in S) = p({x_i}|{{y}},{x_j},j \in {\eta _i})$

(1)

其中， ${\eta _i}$ 为位置i的邻域系统，S表示一个定义有邻域系统的有限集合，那么此时(x, y)称为一个条件随机场^[8]。

若x是关于特征y的标记，且 $C = \{ \{ {{{y}}_c},{x_c}\} \} $ 是邻域系统上的基团集，则关于标记x的CRF模型为：

$p(x|{{y}},\theta ) = \frac{1}{{Z\left( {{{y}},\theta } \right)}}\exp \left\{ {\sum\limits_{c \ \in C} {{\phi _c}\left( {{x_c},{{y}},\theta } \right)} } \right\}$

(2)

其中， $Z({{y}},\theta ) =\displaystyle \sum\nolimits_x {\exp \left\{\displaystyle \sum\nolimits_{c \ \in C} {{\phi _c}({x_c},{{y}},\theta )} \right\} } $ 为归一化函数； ${\phi _c}{\rm{(}}{x_c}{\rm{,}}{{y}}{\rm{,}}\theta {\rm{)}}$ 是定义在基团c上带有参数 $\theta $ 的势函数。

假设用 $x = {({x_s})_{s \in S}}$ 表示标记图像， ${{y}} = {({{{y}}_s})_{s \in S}}$ 表示观测图像。当只考虑单位置基团和双位置基团时，式(2)给出的条件随机场数学表达式可以进一步表示为：

$p\left( {x\left| {\mathit{{y}},\theta } \right.} \right) = \frac{1}{{Z\left( {\mathit{{y}},\theta } \right)}}\exp \left\{ {\sum\limits_{i \in S} {{\phi _i}\left( {{x_i},\mathit{{y,w}}} \right)} + \sum\limits_{i \in S} {\sum\limits_{j \in {\eta _i}} {{\phi _{ij}}\left( {{x_i},{x_j},\mathit{{y,v}}} \right)} } } \right\}$

(3)

其中， ${\phi _i}( \cdot )$ 和 ${\phi _{ij}}( \cdot )$ 分别表示具有参数w和参数v的单位置势函数和双位置势函数； $\theta $ 表示参数集 $\theta = \{ {{w}},{{v}}\} $ 。

2.2 势函数

针对不同的应用背景，需要采用不同的势函数。常见的势函数包括多元对数回归(Multinomial Logistic Regression, MLR)^[17]、Boost^[18]、支持向量机(Support Vector Machines, SVM)^[19]、多项式函数^[20]等。MLR分类器不需要观测数据满足正态分布等限制条件，可以适应更多的观测数据，因此本文选择MLR分类器作为单位置势函数^[8]：

${\phi _i}({x_i},{{y}},{{w}}) = \sum\limits_{l = 1}^L {\delta ({x_i} = l)} \log p({x_i} = l|{{y}},{{w}})$

(4)

其中， $\delta ( \cdot )$ 表示Kronecker delta函数，且：

$p({x_i} = l|{y},{w}) = \left\{ {\begin{array}{*{20}{c}}{\frac{{\exp \left({w}_l^{\rm{T}}{{y}_i}\right)}}{{1 +\displaystyle \sum\limits_{k = 1}^{L{\rm{ - 1}}} {\exp \left({w}_k^{\rm{T}}{{y}_i}\right)} }}{\rm{,\; if }}\; l < L}\\{\frac{1}{{1 +\displaystyle \sum\limits_{k = 1}^{L - 1} {{\rm{exp}}\left({w}_k^{\rm{T}}{{y}_i}\right)} }}{\rm{,\; if }}\; l = L}\end{array}} \right.$

(5)

其中， $l \in \{ 1,2, ·\!·· ,L\} $ 且L表示图像的类别数目；w_k为对应第k类的参数向量 ${\left[ {{w_{k1}},{w_{k2}}, ·\!·\!· ,{w_{kD}}} \right]^{\rm{T}}}$ ; w表示所有的w_k( $k = 1,2, ·\!·\!· ,L - 1$ )首尾相接得到的参数向量，上标T表示转置。

双位置势函数可以表达图像空间的上下文信息，本文选择如式(6)所示的广义Ising/Potts模型作为双位置势函数模型^[8]：

$\begin{aligned}{\phi _{ij}}({x_i},{x_j},{{y}},{{v}}) = & \sum\limits_{k,l \in \{ 1, 2, \cdots ,L\} } {{{{v}}_{kl}^{\rm{T}}}} \\&\cdot {{{g}}_{ij}}({{y}}) \delta ({x_i} = k)\delta ({x_j} = l)\end{aligned}$

(6)

其中，v_kl为参数向量，v表示所有的v_kl( $k,l = 1,$ $2, ·\!·\!· ,L$ )首尾相接得到的参数向量， ${{{g}}_{ij}}\left( \cdot \right)$ 表示从整个观测数据提取的位置对(i, j)的特征向量， $\delta ( \cdot )$ 表示Kronecker delta函数，上标T表示转置。

3 组合条件随机场模型

CRF分类器利用多特征的方式为：把从图像中任一位置提取得到的多种特征首尾相接而堆叠形成特征矢量，并以这个特征矢量作为分类器的输入矢量。这种利用多特征的方式，不仅操作简单，而且理论上采用的特征越多，得到的分类精度应该越高，但实际中这种方式容易引起特征干扰和过拟合问题，从而影响最终的分类精度。为了更好地利用多种特征信息，同时避免出现特征干扰和过拟合问题，本文提出采用组合CRF模型来提高极化SAR图像的地物分类精度。

3.1 组合模型

组合模型是利用多个子分类器组合分类来获得比单个分类器更高的分类精度。组合模型结合决策树的思想在机器学习领域应用非常广泛，这种思想通常用来解决单个决策树判别能力不足以及容易产生过拟合的问题^[21]。本文根据这种思想提出一种组合CRF模型。组合CRF模型主要分为两部分：(1)利用特定的策略得到多个有差异性的子分类器；(2)使用一种规则将多个子分类器融合。为得到有差异性的子分类器，本文将提取的特征分成多个子特征矢量分别训练同一个CRF模型。对于组合子分类器的规则，研究工作者给出了大量的组合方法，包括投票表决法^[21]、Boosting方法^[8]等。其中投票表决法是较早提出并取得广泛应用的方法，成为比较和评估新提出的融合规则的基准。为得到组合CRF模型，首先提取训练样本的K个子特征矢量，然后利用K个子特征矢量训练得到K个有差异的子分类器，最后使用融合公式将K个子分类器融合从而得到最终的组合CRF模型。

3.2 特征组构建

本文首先提取了4种类型的特征，包括基于功率测量的特征^[21]、基于目标分解的特征^[22,23]、基于形态学的特征^[21]、基于灰度共生矩阵(Gray Level Co-occurrence Matrix, GLCM)的纹理特征^[24]，然后将这些特征分成3组子特征矢量。表1为划分后的3组子特征矢量，分别用 $\{ f_i^k({{y}}),k = 1,2,3\} $ 表示。3组子特征矢量将作为输入用于训练CRF模型得到3个子CRF分类器。

3.3 融合规则

对极化SAR图像的任一位置i，提取的K种类型的子特征矢量可以表示为 $f_i^{1:K}({{y}}) = \{ f_i^1({{y}}),$ $f_i^2({{y}}), ·\!·\!· ,f_i^K({{y}})\} $ ，其中 $f_i^k({{y}}) = [f_{i1}^k({{y}}),f_{i2}^k({{y}}), ·\!·\!· ,$ $f_{iD}^k({{y}})]{\rm{, }}1 \le k \le K$ 表示图像位置i处的第k种类型特征提取到的D维特征，则第k种类型特征表示为 ${f^k}({{y}}) = \{ f_i^k({{y}}),i \in S\} $ ，其中S表示一个定义有邻域系统的有限集合。用 $f^{1:K}({{y}}) = \{ f^1({{y}}),f^2({{y}}),·\!·\!· , $ $f^K({{y}})\} $ 表示输入图像的特征y，首先将K个子特征矢量分别训练同一个CRF模型得到K个有差异性的子CRF分类器，然后使用式(7)的组合公式将子分类器融合。

$p\left(x|{f^{1:K}}({{y}})\right) = \sum\limits_{k = 1}^K {{\alpha _k}p\left(x|{f^k}({{y}})\right)} $

(7)

其中， $p\left(x|{f^k}({{y}})\right)$ 表示第k个子CRF分类器的分类结果； ${\alpha _k}$ 表示第k个子CRF分类器在组合公式中的自适应权值系数，取值范围为 ${\alpha _k} \in \left[ {0,1} \right]$ 。在本文的实验中，为了简便地得到每个子分类器对应的自适应权值系数，利用选定的测试样本测试子分类器并得到对应的分类精度，最后将所有子分类器得到的分类精度归一化得到 ${\alpha _k}(k = 1,2, ·\!·\!· ,K)$ 。

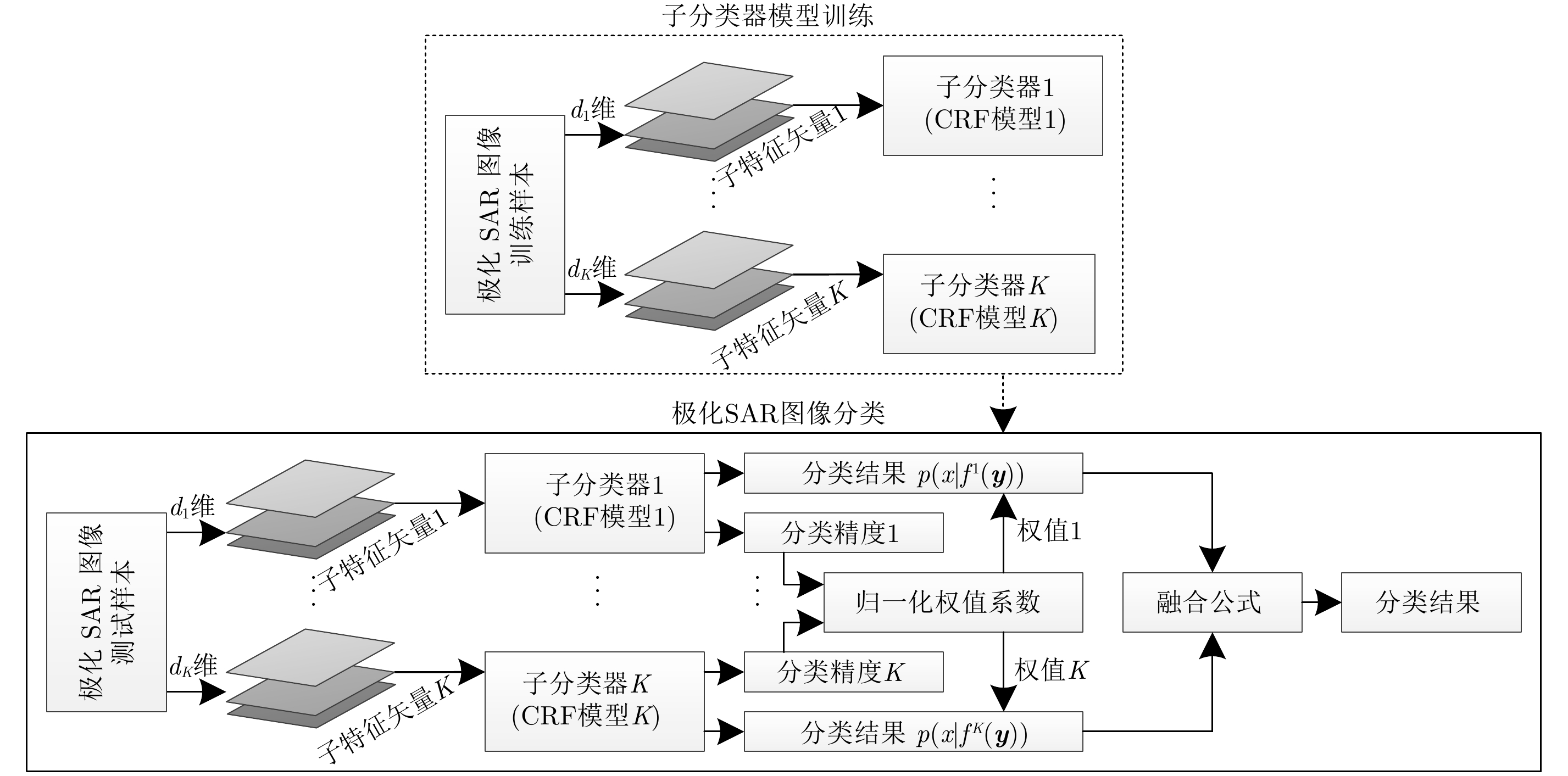
为了清楚地说明本文的算法过程，图1给出了本文基于组合CRF模型的极化SAR图像分类流程图。

4 实验结果与分析 4.1 实验数据

为了对本文提出算法的性能进行分析和评估，我们选择了两组实测极化SAR图像数据进行实验。图2(a)是由NASA/JPL提供的尺寸为750×1024像素的荷兰Flevoland地区极化AIRSAR图像数据。图2(c)是由German Aerospace Center提供的尺寸为1300×1200像素的德国Oberpfaffenhofen地区的E-SAR图像数据。图2(a)和图2(c)中的红色方框表示本文方法在这两组实测数据中选择的训练样本，图2(b)和图2(d)分别为两幅极化SAR图像对应的真值地物图，两幅真值地物图分别标记有11种和5种地物类别。

4.2 实验验证 4.2.1 Flevoland地区极化SAR图像实验

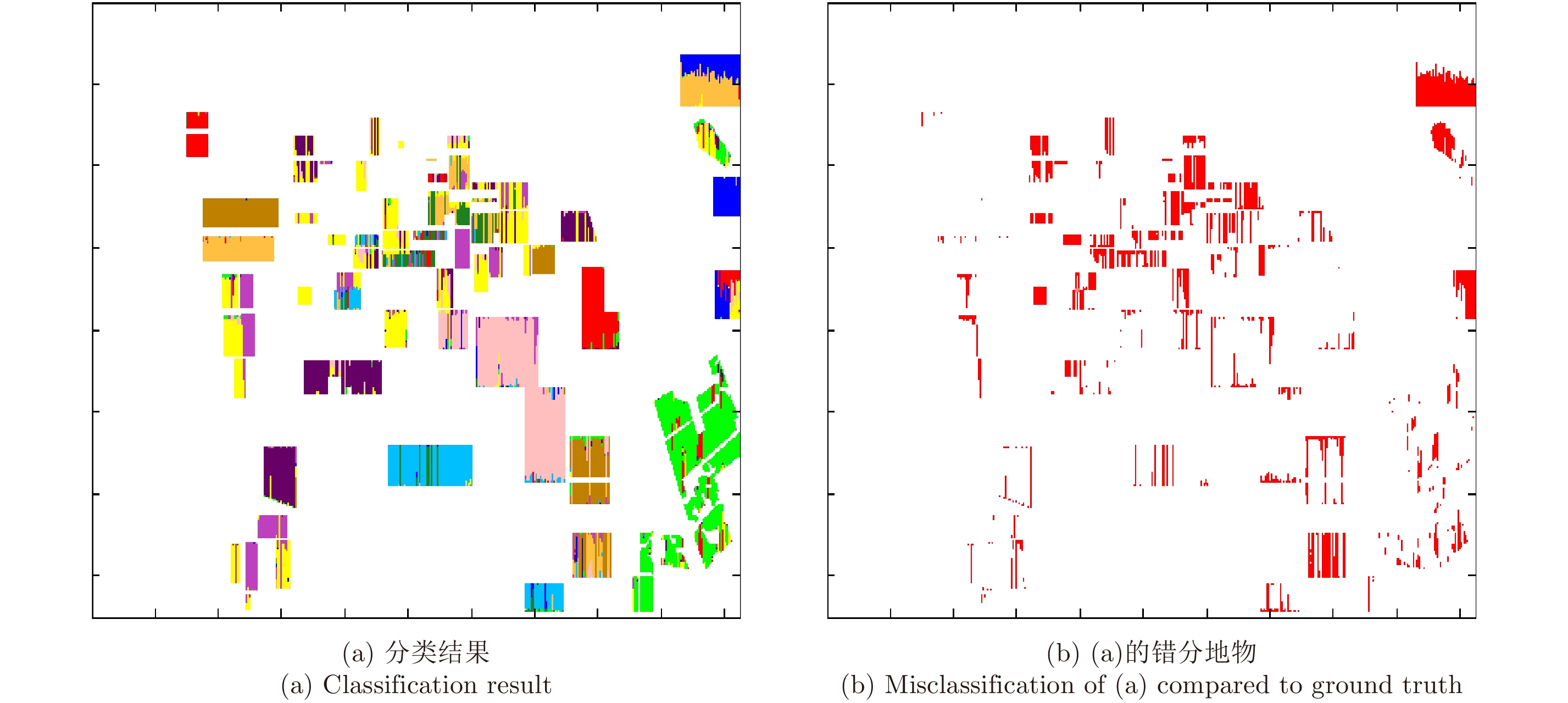
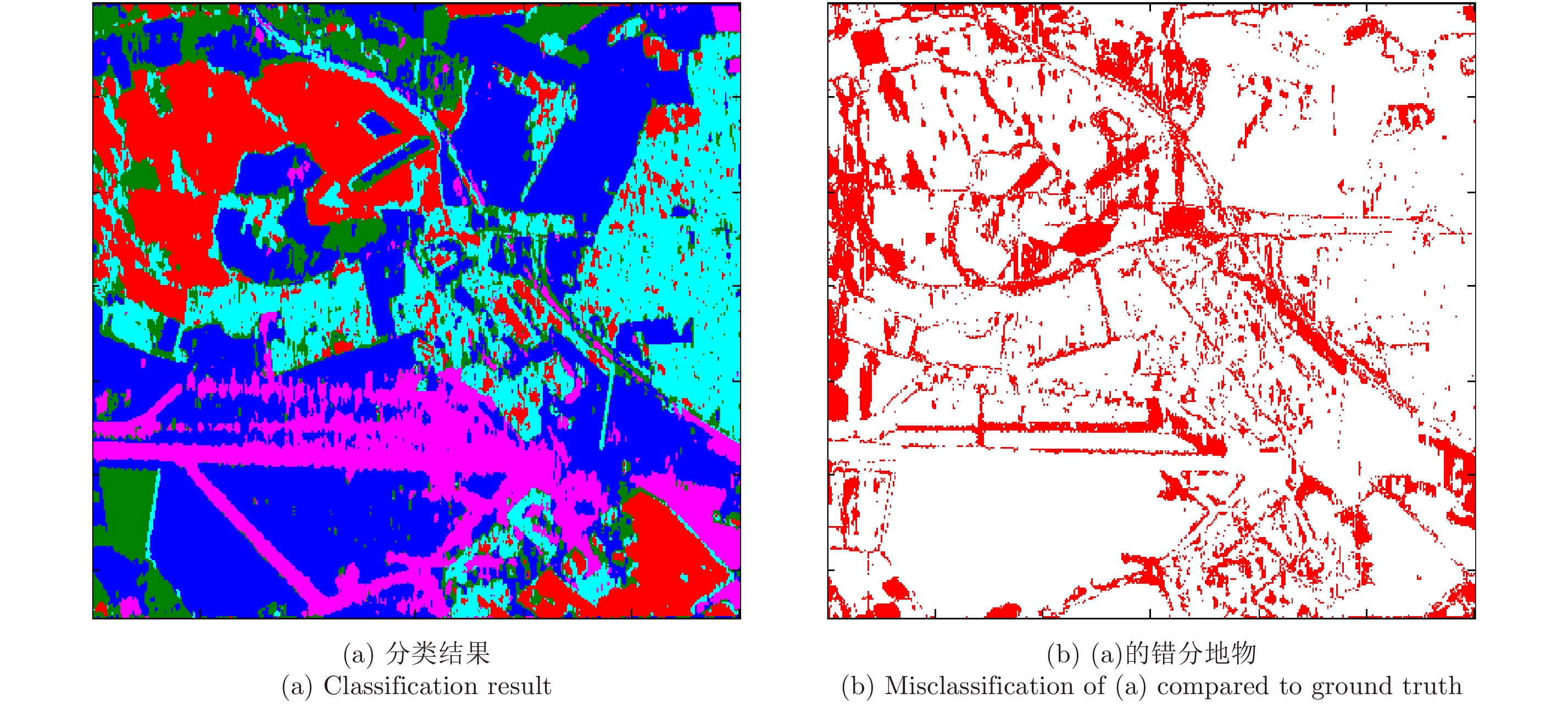
本文首先将从Flevoland地区极化SAR图像中提取的3组特征矢量以首尾相接的堆叠方式组成共31维的特征矢量用于训练单个CRF模型得到CRF分类器。图3(a)和图3(b)分别为基于堆叠特征的CRF分类器的分类结果以及分类结果与真实地物图相减得到的错分地物图，表2为分类结果的混淆矩阵。

从图3(a)，图3(b)和表2可以看出，基于堆叠特征方式得到的分类结果较差，总体分类精度只有74.06%。尤其是草地和水体两类地物被大量地错分，分类精度分别只有30.92%和59.50%。这说明高维特征矢量虽然可以表征图像更多的信息，但是，由于存在特征之间的相互干扰以及分类器过拟合问题，从而导致分类精度不高。

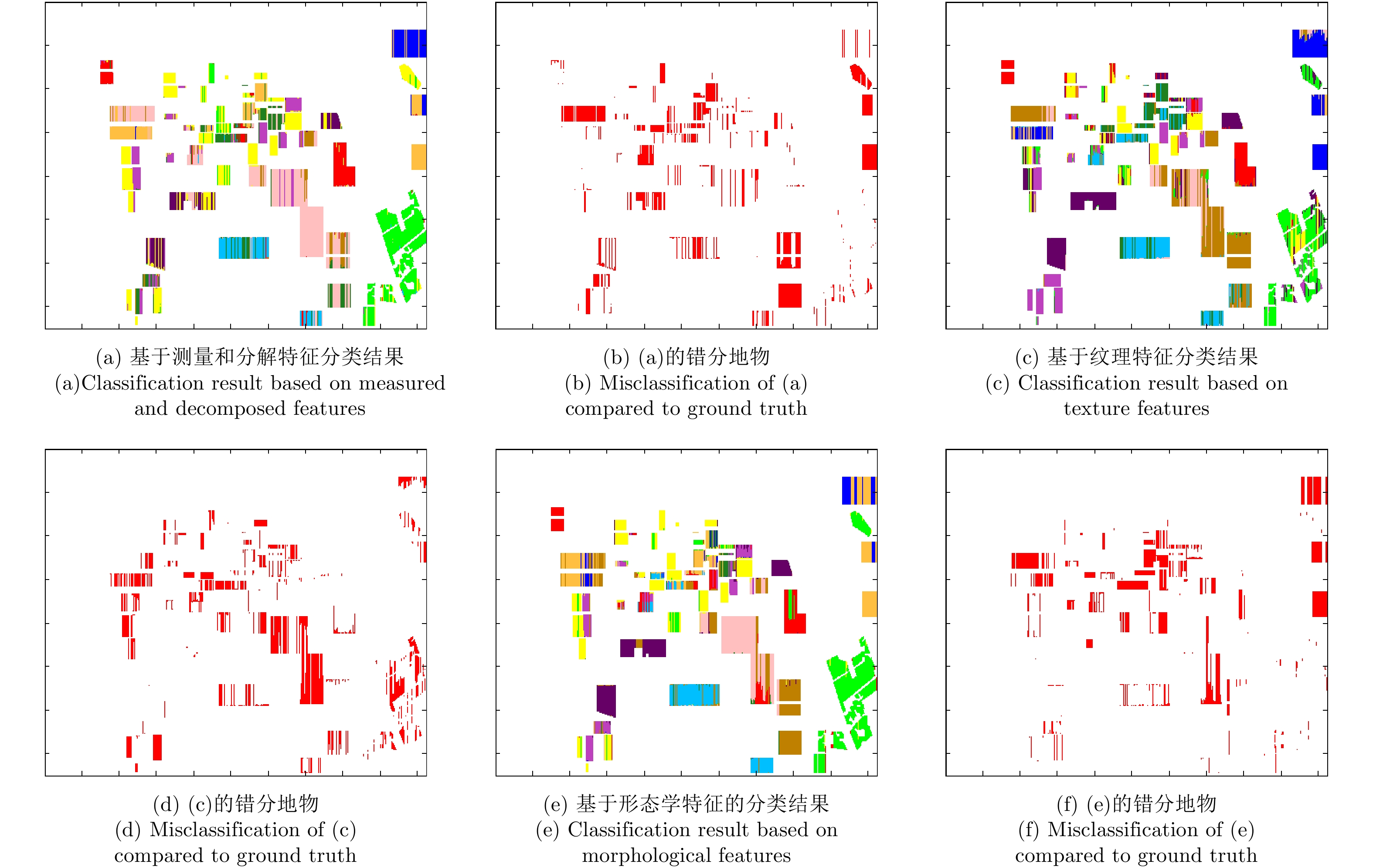
图4(a)–图4(f)分别为基于测量数据的特征和分解特征、纹理特征、形态学特征3组特征矢量分别训练同一个CRF模型得到的子分类器的分类结果图以及错分地物图。从图4中可以看出，各个子分类器比基于堆叠特征的CRF分类器的分类效果差，其原因为：虽然单个子分类器采用了较少的特征，减少了特征之间的相互干扰，但是较少的特征只包含了较少的地物信息，导致子分类器对地物的分类能力较弱；同时，由于子分类器使用不同的特征组进行训练，因此，对同一地物具有不同的分类能力。如图4(c)中水体基本分类正确，而图4(a)和图4(e)中与水体对应的像素点基本被错分。

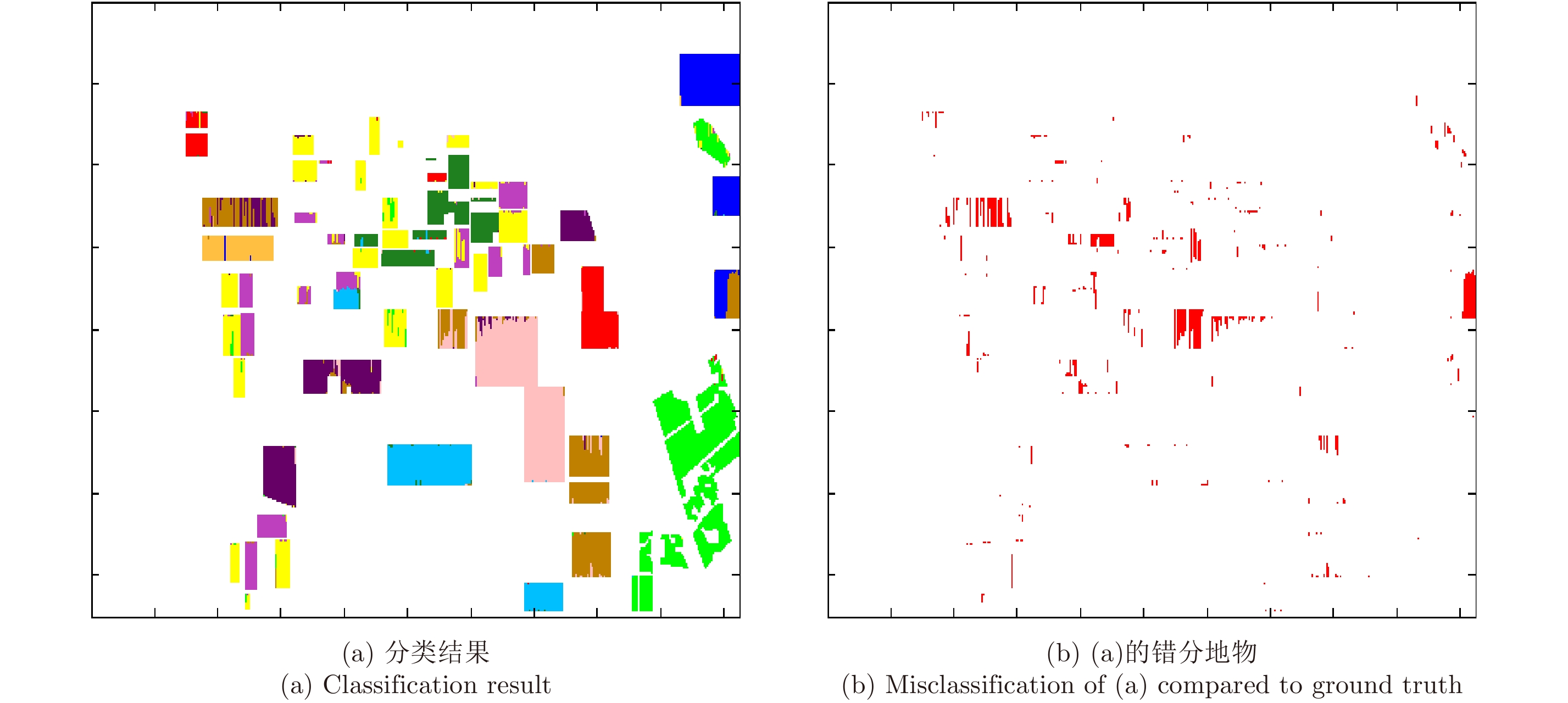
图5为组合CRF模型的分类结果图和错分地物图，表3为分类结果的混淆矩阵。在本文实验中，通过使用各个子分类器先对图2(a)对应的图像数据进行分类得到3个总体分类精度，然后对3个分类精度归一化得到最终的 ${\alpha _i}\left( {i = 1,2,3} \right)$ ，取值分别为0.4877, 0.2040和0.3083。对比观察图3、图4和图5的分类结果，可以看出组合CRF模型的分类结果有很大的改善。组合CRF分类器的分类结果优于基于堆叠特征的CRF分类器和各个子分类器的分类结果。同时，对比表2和表3，组合CRF分类器总体分类精度从74.06%提高到87.44%，尤其是草地和水体两种地物在组合CRF分类器中分类精度分别达到了83.76%和88.86%，这也进一步说明了组合CRF分类器的有效性。

上述实验结果表明，由于组合CRF分类器解决了特征干扰以及过拟合问题，模型在训练的时候可以充分地获取图像特征表达的本质信息，而且组合分类器能够综合利用各个子分类器的优势，因此，组合CRF分类器可以获得比基于堆叠特征的分类器和各个子分类器更高的分类精度。

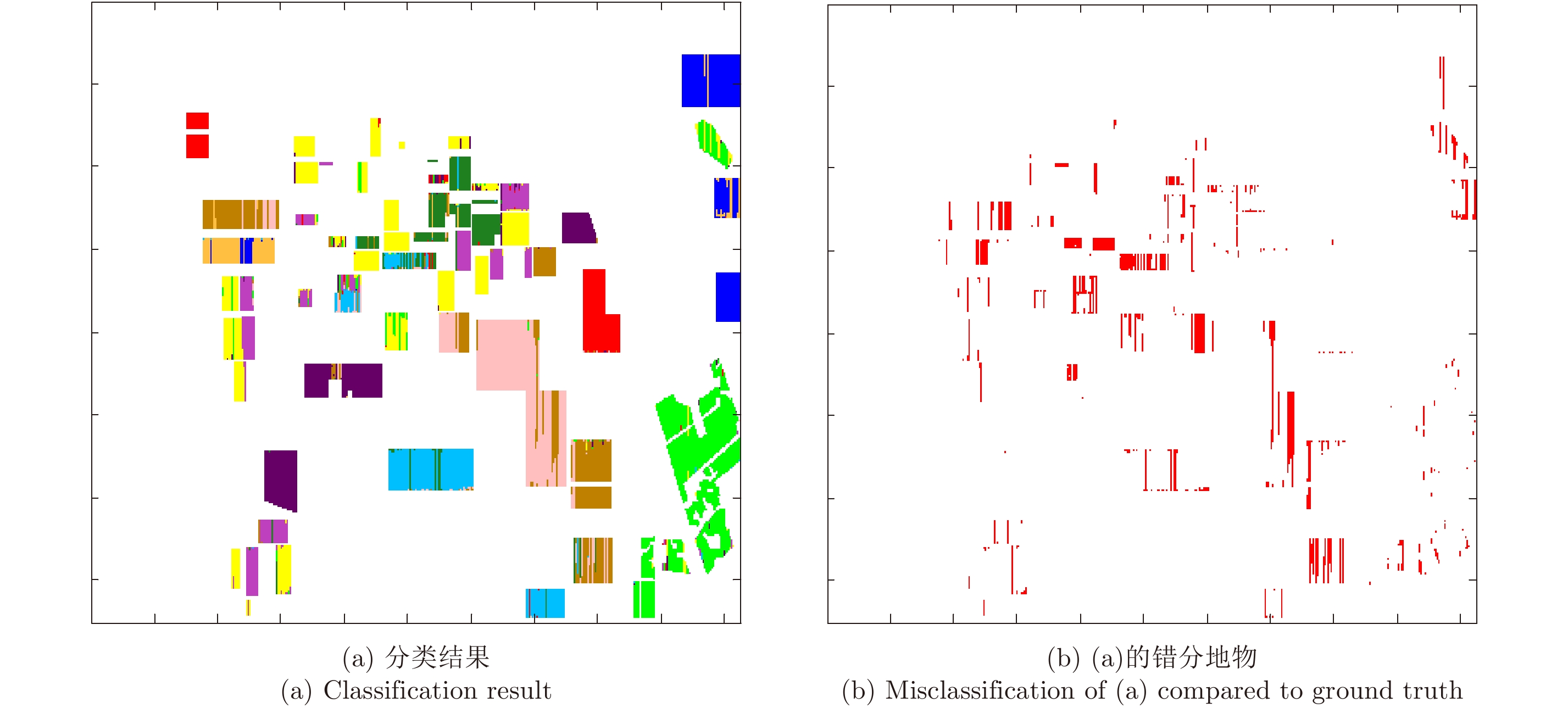
由本文引言中的介绍可以知道，特征选择(也称为特征稀疏化处理)也可以用来解决特征干扰和过拟合问题，其中l-1正则化法是一种广泛使用并且效果较好的方法^[8]。作为对比，图6给出了基于l-1正则化法的CRF分类器对Flevoland地区极化SAR图像的分类结果以及错分地物图。对比图5和图6可以看出，组合CRF分类器与利用l-1正则化法进行特征选择得到的CRF分类器的分类效果基本一致，其中图6的总体分类精度为86.96%(限于篇幅，我们未给出相应的分类精度表)，略小于图4的总体分类精度87.44%。这个实验表明，相比于基于l-1正则化法的CRF分类器，组合CRF分类器解决特征干扰和过拟合问题具有更好的效果。

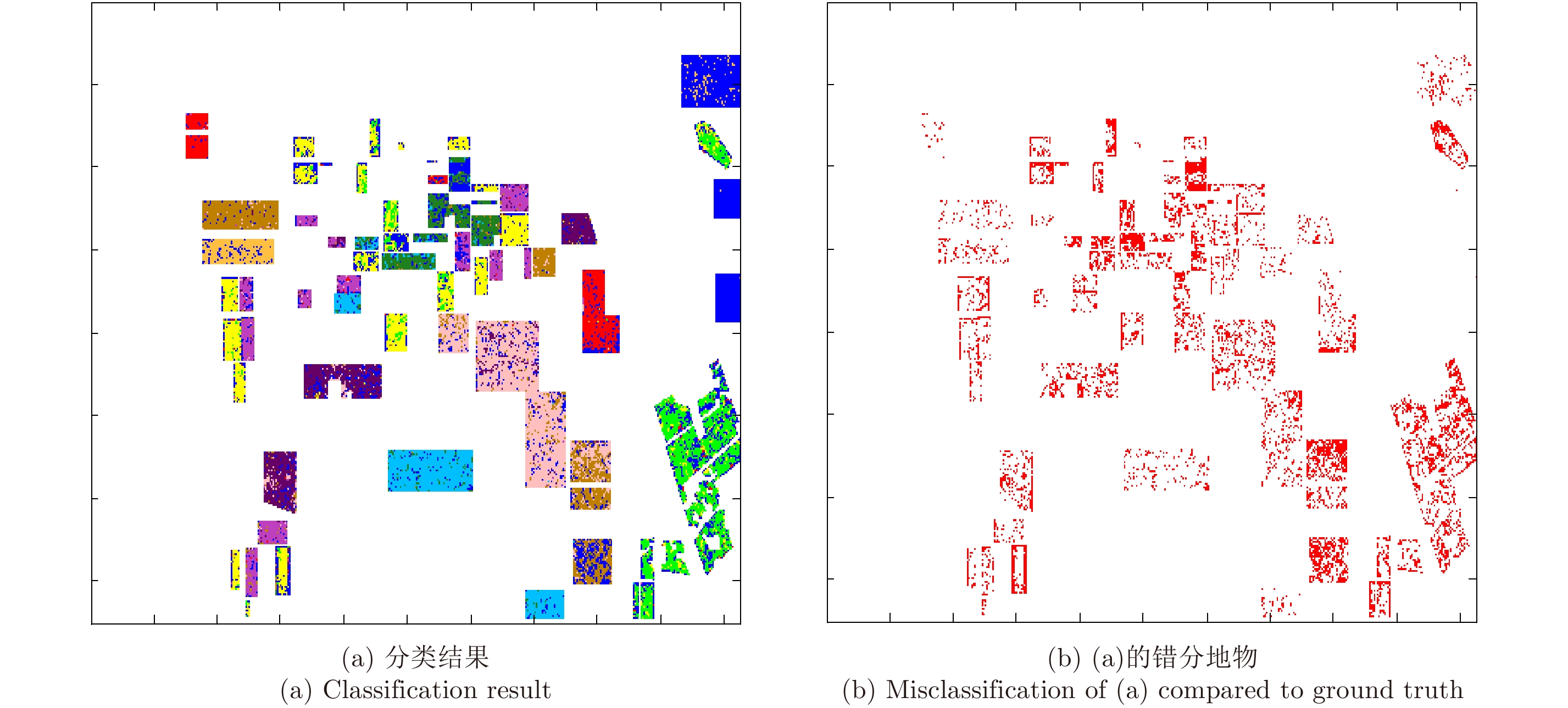
为了更好地评估本文方法的分类性能，我们还利用目前机器学习领域非常流行的SVM分类器对Flevoland地区极化SAR图像进行了分类。观察图7中利用SVM分类器的分类结果(限于篇幅，我们未给出相应的分类精度表)并且与图5的分类结果进行对比，可以发现组合CRF模型的分类性能有较大的优势，图5比图7的分类精度高13.78%。这说明组合CRF分类器在对极化SAR图像分类时，通过有效利用上下文信息并且减少特征干扰可以取得更好的分类性能。

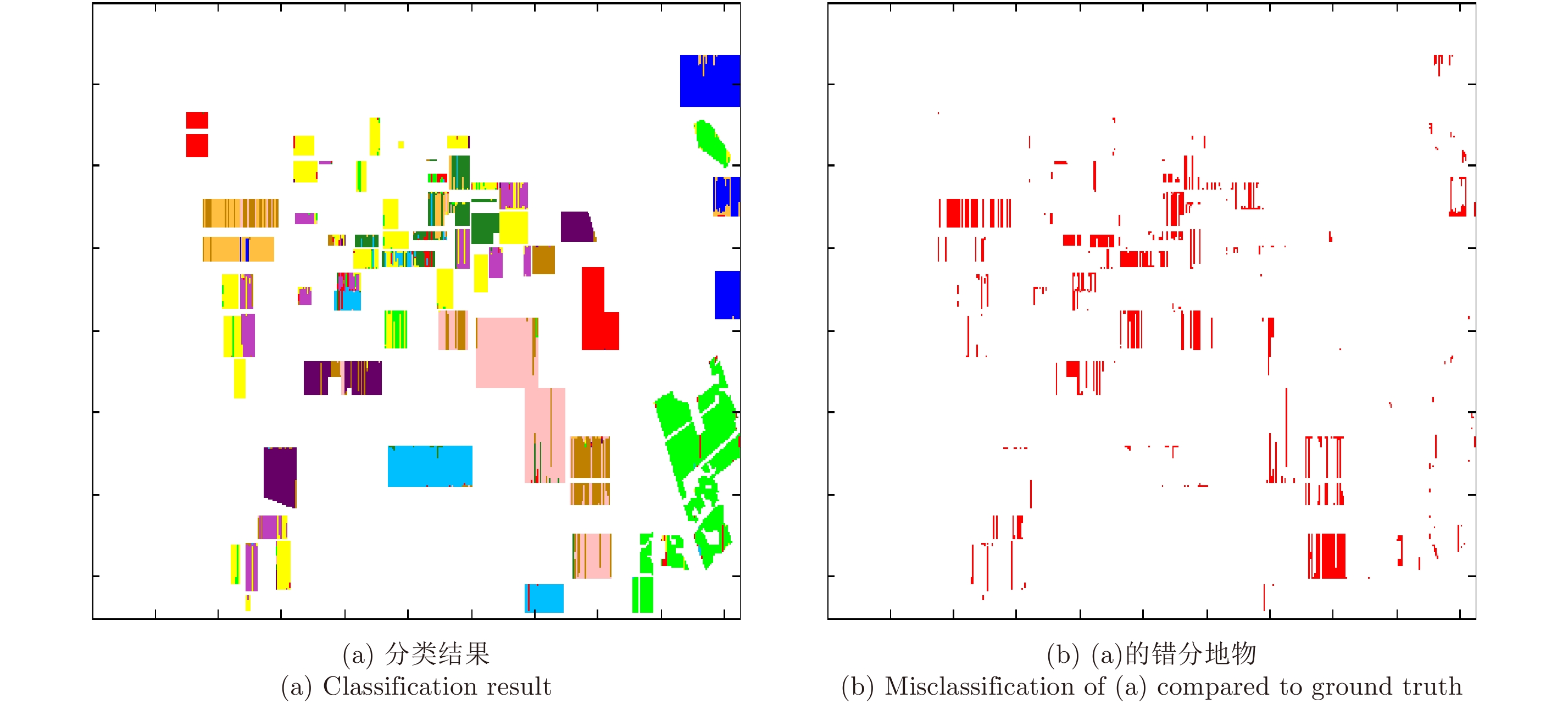
此外，为了验证本文提出的融合公式的有效性，图8给出了基于投票表决法的组合CRF模型分类结果和错分地物图，对比发现本文的组合CRF分类器模型分类结果优于投票表决法。基于投票表决法的组合CRF分类器取得了83.94%的分类正确率(限于篇幅，我们未给出相应的分类精度表)，低于本文提出的组合CRF模型87.44%的总体分类精度，表明本文提出的融合公式对融合子分类器有较好的效果。

4.2.2 Oberpfaffenhofen地区极化SAR数据实验

为了进一步说明本文方法的适用性，我们利用本文方法对Oberpfaffenhofen地区极化SAR图像数据也开展了分类实验。图9(a)和图9(b)为基于堆叠特征的CRF分类器分类结果，表4为分类结果的混淆矩阵。基于堆叠特征的CRF分类器的总体分类精度为66.78%，且分类结果中用红色标记的林地分类结果较差。

图10为各个子分类器的分类结果及错分地物图。观察各个子分类器的分类结果，可以得出基于测量数据和分解特征的CRF分类器取得了较好的分类结果，但3个子分类器结果均比图9的分类结果差，表明测量数据特征和分解特征包含较多的表征Oberpfaffenhofen地区极化SAR图像的目标信息，但是各个子分类器均不能全面表征图像目标信息。同时观察发现，图10(a)中黑色方框标注的区域出现了明显的错分，但在图10(e)中此区域被基本正确分类。这是由于不同类型的特征包含了不同的目标信息，因此，各个子分类器对不同地物的分类能力也不同。

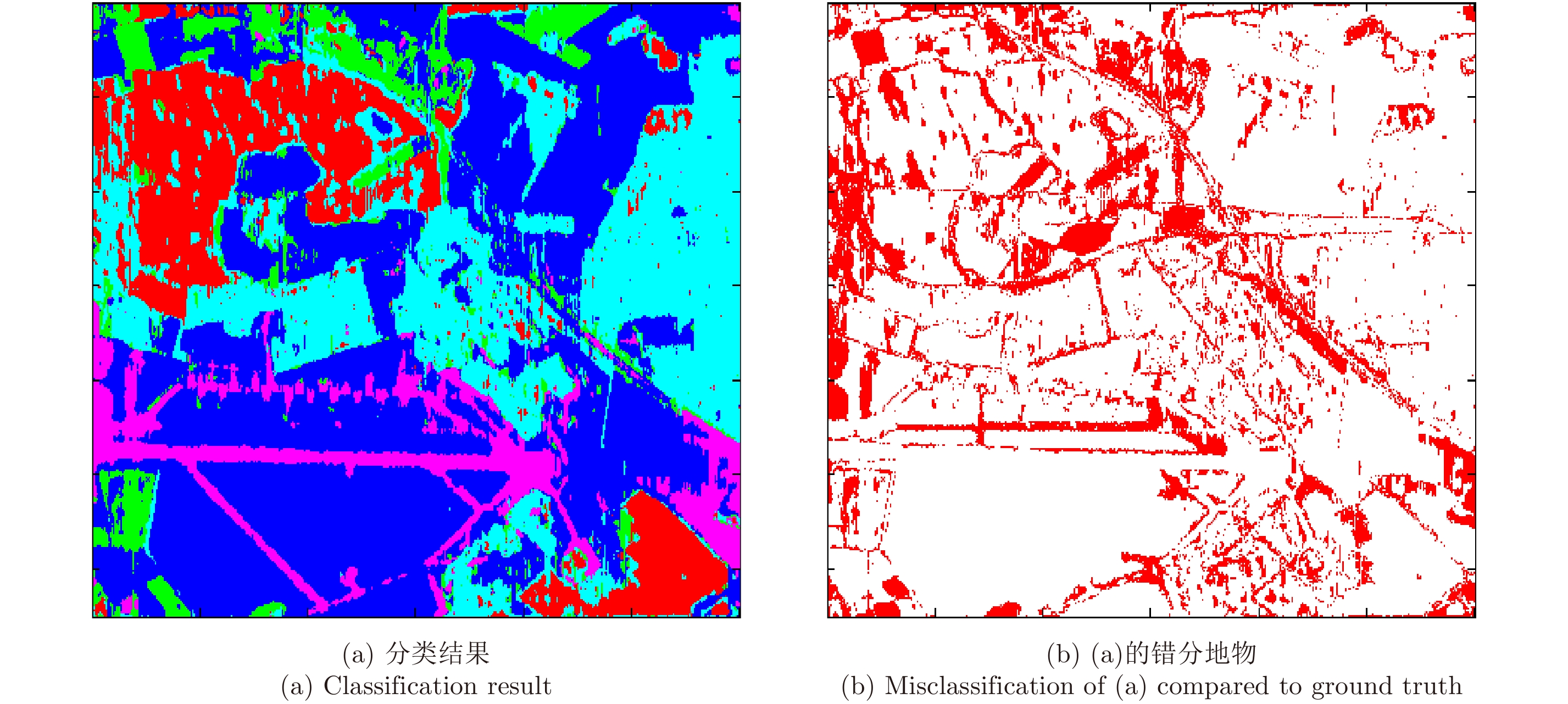
图11为组合CRF分类器分类结果图及错分地物图，表5为组合CRF分类器的分类结果混淆矩阵。在本文实验中，通过使用各个子分类器先对图2(c)对应的图像数据进行分类得到3个总体分类精度，然后对3个分类精度归一化得到最终的 ${\alpha _i}\left( {i = 1,2,3} \right)$ ，取值分别为0.5783, 0.1330和0.2887。

图12为基于l-1正则化法进行特征选择后的CRF分类器分类结果和错分地物图。观察对比发现其与组合CRF分类器的分类效果基本相同，进一步验证了组合分类器在解决特征干扰时的有效性。

图13为SVM分类器对Oberpfaffenhofen地区极化SAR数据分类结果和错分地物图。与组合CRF分类器结果相比，SVM分类器得到的分类精度(63.58%，限于篇幅，我们未给出相应的分类精度表)与组合CRF分类器的分类精度(78.33%)存在较大的差距，这说明组合CRF分类器可以充分地利用特征信息和上下文信息来提高分类器性能。

通过对比图11和图13及表4和表5可以发现，组合CRF分类器的效果有较大的提升，而且组合分类器的分类精度达到78.33%，比基于堆叠特征的CRF分类器的分类精度(66.78%)提高了11.55%。这表明组合CRF分类器可以有效地解决基于堆叠特征的CRF分类器出现的特征干扰等问题，同时可以综合利用各个子分类器对不同地物分类性能的优势来提高分类精度。

图14为基于投票表决法的组合CRF分类器的分类结果和错分地物图，其总体分类精度为73.02% (限于篇幅，我们未给出相应的分类精度表)。上述实验结果表明，本文提出的组合CRF模型的分类精度优于投票表决法，同时也验证了本文提出的融合公式的有效性。

5 结论

在极化SAR图像地物分类中，为了解决基于堆叠特征的CRF模型由于特征干扰和过拟合问题而导致分类器分类精度下降的问题，本文提出了一种组合CRF分类模型用于极化SAR图像地物分类。该模型首先将提取的极化SAR图像多种特征进行分组，然后利用各个特征组分别训练同一个CRF模型得到多个有差异性的子分类器，再通过融合公式融合各个子分类器的分类结果得到最终的组合CRF模型分类结果。利用两组实测极化SAR图像数据的实验结果表明，本文提出的组合CRF模型不仅能够有效地解决由于特征堆叠而引起的特征干扰和过拟合问题，而且能够充分地利用各个子分类器的性能优势，在对极化SAR图像分类时取得了较好的分类结果。