在传统跟踪方法中，目标假设为点目标，只占据一个分辨单元，但随着传感器分辨率的提高，目标将占据多个分辨单元，称该类目标为扩展目标。检测前跟踪算法是低信杂噪比(Signal To Clutter Noise Ratio, SCNR)下对目标进行处理的一种多帧信号积累方法，它使用传感器原始量测数据，并通过多次扫描量测数据的积累来提高信噪比，而粒子滤波(Particle Filter, PF)方法非常适合处理这类问题。Salmond^[1]在2001年第1次明确提出PF-TBD的概念，并将该方法应用于凝视型光电传感器的单目标检测与跟踪处理中。2005年，Rutten^[2]提出了一种针对观测噪声为Rayleigh情形下的PF-TBD算法。TSOU Haiping^[3]提出了基于极大似然估计的扩展目标跟踪算法，研究了目标发生旋转时的跟踪问题。Gilholm K^[4]利用多假设Kalman滤波来实现扩展目标跟踪，并分析了扩展目标中具有空间分布的散射点。Franken D^[5]提出扩展目标模型为对称正定随机矩阵，并用Bayes方法分析和解决该问题。Ling Fan^[6]建立椭圆模型，并在状态向量中加入目标存在变量和目标形状参数。针对雷达扩展目标，吴兆平^[7]利用传感器获得的数据，确立更接近于实际的线性扩展模型，并推导出了扩展模型的似然比函数，同时，对原始的粒子滤波算法进行了优化。为实现隐身扩展目标的检测与跟踪，于洪波^[8,9]将目标强度和空间长度引入状态向量，利用粒子滤波实现目标的跟踪和目标长度的估计。

上述问题只考虑Gaussian噪声下的微弱目标检测问题，没有考虑有杂波的情况。例如，当雷达工作于下视状态时，经过空时自适应(Space-Time Adaptive Processing, STAP)技术抑制杂波后的量测数据除了受噪声影响外还受剩余杂波的影响，使得传统基于噪声假设的量测模型不准确。同时，随着雷达性能的改善，研究者发现地(海)杂波出现了很长的波动，其杂波的统计特性明显偏离高斯分布。当高分辨雷达处于低视角观测时，通过考察地(海)杂波发现^[10–12]，Weibull分布能较好地刻画实际环境中的杂波统计特性。

针对杂波环境下微弱扩展目标的检测与跟踪问题，本文以杆状物体作为研究对象，对距离和方位进行划分，并给出不同区域上含有Weibull杂波的传感器量测模型。利用扩散函数，在点目标的基础上，推导了扩展目标的似然函数以及粒子权重的计算。在状态向量中加入目标存在状态以及目标形状参数，利用粒子滤波算法分别实现扩展目标状态和形状参数的检测和估计。仿真实验表明，杂波环境下基于粒子滤波的微弱扩展目标检测前跟踪算法具有较好的稳定性。

考虑x-y平面内运动的杆状目标，目标状态转移具有如下形式：

其中，目标的状态 ${x_k} = {\left[ {\begin{array}{*{20}{c}}{{x_k}}&{{{\dot x}_k}}&{{y_k}}&{{{\dot y}_k}}&{{I_k}}&{{l_k}}\end{array}} \right]^{\rm T}}$ , (x_k, y_k), $\left( {{{\dot x}_k},{{\dot y}_k}} \right)$ 分别表示目标中心的位置、速度，I_k, l_k分别表示扩散目标的强度和空间长度，v_k为过程噪声。用E_k对目标存在状态建模，且描述为2态Markov链，定义目标“新生”概率P_b $\buildrel \Delta \over = $ P $\left\{ {{E_k}\!=\! 1|{E_{k - 1}} \!=\! 0} \right\}$ 和“死亡”概率P_d $ \buildrel \Delta \over =$ P{E_k=0|E_k–1=1}，其中，E_k=0表示目标不存在，E_k=1表示目标存在，则Markov转换概率矩阵为：

考虑经过脉冲压缩处理后的雷达距离-多普勒量测数据。假设距离和方位分别包含N_r和N_a个单元，距离和方位的分辨率分别为${{\Delta }_{\text{r}}}$和${{\Delta }_{\text{a}}}$，用 $\varOmega$ $ \ \ \buildrel \Delta \over = \ \ $ $\left\{ {1,2, \cdots ,{N_{\rm r}}} \right\}$ 和K $ \buildrel \Delta \over = $ $ \left\{ {1,2, \cdots ,{N_{\rm a}}} \right\}$ 来表示距离和方位上的分辨单元集合。对于距离向^[13]，由于目标的扩展，目标回波所占距离单元表示如下：

其中， $\left\lceil X \right\rceil $ 表示向上求整， ${r_k} = \sqrt {x_k^2 + y_k^2} $ , $L\left( {{x_k}} \right)$ 表示目标距离向长度。

对于方位向，目标回波所占的方位单元表示如下：

其中， ${a_k} = \arctan\left( {{y_k}/{x_k}} \right)$ , V(x_k)表示目标方位向长度。

假设雷达在相同扫描区域已经产生多帧距离-多普勒图像，z_k(i, j)表示k时刻量测数据，具体形式为：

式中， $i = 1,2, \cdots ,{N_{\rm r}},j = 1,2, \cdots ,{N_{\rm a}}$ , h_k(i, j)为目标在分辨单元(i, j)处的信号，n_k(i, j)表示在(i, j)处的杂波，v_k(i, j)为量测噪声，假设为零均值、方差为 $2{\sigma ^2}$ 的复高斯噪声。h_k(i, j)表示散射点对分辨单元(i, j)的强度影响，一般情况下h_k(i, j)可近似为2维高斯分布形式^[14,15]，则散射点在传感器分辨单元(i, j)的强度影响为^[7]：

其中 ${Σ} $ 为已知参数，表示传感器模糊斑点数量。k时刻的量测数据可表示为 ${z_k} = \{ {z_k}(i,j),i = 1, ·\!·\!· , $ ${N_{\rm r}},j = 1, ·\!·\!· ,{N_{\rm a}}\} $ ，直到k时刻的完整量测数据集合表示为 ${Z_k} = \left\{ {{z_i},i = 1, ·\!·\!· ,k} \right\}$ 。

在实际雷达环境中，存在许多地物、海和云雨等各种杂波，经研究表明^[12]，Weibull分布在一定程度内可以与实际杂波吻合。因此，设 $\left| {n_k^{\left( {i,j} \right)}} \right|$ 符合以下Weibull分布，即

其中，p为形状参数，q为尺度参数。

设 ${z'\!\!_k}\left( {i,j} \right) = \left| {{h_k}\left( {i,j} \right) + {v_k}\left( {i,j} \right)} \right|$ 表示信号加噪声幅度，对于分辨单元(i, j)，当E_k=1时， ${z'\!\!_k}\left( {i,j} \right)$ 近似服从非中心的2阶卡方分布，即

当E_k=0时，分辨单元(i, j)内信号的幅度近似服从瑞利分布^[13]，即

在目标存在时，考虑Weibull杂波因子，量测值z_k(i, j)的幅度服从非中心卡方分布与Weibull的混合分布，借用文献[16]的思想，根据混合概率密度公式

得到似然函数：

同上，当E_k=0时，量测值z_k(i, j)的幅度服从瑞利分布与Weibull分布的混合分布，则相应的似然函数为：

式中， $\rho $ 和 $\varepsilon $ 为比例系数( $\rho \in \left[ {0,1} \right],\varepsilon \in \left[ {0,1} \right]$ )。

随着雷达分辨率的提高，目标的物理尺寸大于距离分辨率，这样就会引起目标在距离和方位上的线性扩展，则扩展目标的似然函数为^[17]：

其中，x_k为中心点， ${\hat x_k}$ 为扩展点； $p\left( {{{\hat x}_k}|{x_k}} \right)$ 表示从点x_k扩展到 ${\hat x_k}$ 的概率密度函数。

目标在距离和方位角发生2维线性扩展。设线性扩展目标长度为N_z，扩展目标的方向与观察者视线方向的夹角为 $\theta $ ，则目标扩展后的坐标范围^[7]为：

其中，(l_k, d_k)表示扩展目标的中心位置。根据以上条件，则其似然函数为：

假设各个(i, j)内的z_k^{(i, j)}是独立的，似然函数可表示为：

式中，C_i(x_k)和C_j(x_k)表示(i, j)内受回波影响的集合。

假设该模型中扩展目标每一时刻仅有限个回波(散射点)时^[18]，设散射点个数为M时，则有：

其中，x_k⁽ⁱ⁾表示在某一时间k相互独立的散射点。

定义似然比为：

因此，对状态为 $x_k^n$ 的目标，将式(8)、式(19)代入式(20)、式(21)中，可以计算出未归一化权重 $\tilde \omega _k^{n}$ 。

下面给出PF-TBD算法^[19]。首先，引入混合状态向量 ${y_k} = {\left[ {x_k^{\rm T} {E_k}} \right]^{\rm{T}}}$ 。设在k–1时刻的联合PDF为 $p\left( {{y_{k - 1}}|{Z_{k - 1}}} \right)$ 可由粒子集 $\left\{ {y_{k - 1}^n,\omega _{k - 1}^n} \right\}_{n = 1}^N$ 来描述，N为粒子数量。则该算法运算步骤如下所示：

步骤1  计算目标的存在变量 $\left[ {\left\{ {E_k^n} \right\}_{n\rm{ = 1}}^N} \right]$ 目标存在变量转移 $\left[ {\left\{ {E_{{k - 1}}^{n}} \right\}_{n\rm{ = 1}}^N,\varPhi } \right]$ ；

步骤2  从X_kⁿ中抽取M个散射点：

步骤3  FOR n=1:N

(1) 对“新生”(即 $E_{{k - 1}}^n = 0,E_k^n = 1$ )粒子采样 $x_k^n \sim {p_\rm{b}}\left( {{x_k}|{z_k}} \right)$ ；

(2) 对“存活”(即 $E_{k\rm{ - 1}}^n = 1,E_k^n = 1$ )粒子采样 $x_k^n \sim p\left( {{x_k}|x_{k\rm{ - 1}}^n} \right)$ ；

(3) 计算权重 $\tilde \omega _k^n$ ；

步骤4  用 $x_k^n \sim {p_\rm{b}}\left( {{x_k}{|}{z_k}} \right)$ 替换权重比较低的 $x_k^n \sim p\left( {{x_k}|x_{k\rm{ - 1}}^n} \right)$ ，并计算相应的权重；

步骤5  归一化粒子权重， $\left\{ \omega _{k}^{n}=\tilde{\omega }_{k}^{n}/\sum\limits_{n=1}^{N}{\tilde{\omega }_{k}^{n}} \right\}_{n=1}^{N}\text{ }$ ；

步骤6  粒子重采样， $\left[ {\left\{ {y_k^n,1/N} \right\}_{n\rm{ = 1}}^N} \right]$ =重采样 $\left[ {\left\{ {y_k^n,\omega _k^n} \right\}_{n\rm{ = 1}}^N} \right]$ 。

目标在k时刻后验PDF为P_k $ \buildrel \wedge \over = $ P{E_k=1|Z_k}，因此

估计目标状态为：

本节将通过仿真实验来说明在杂波环境下基于粒子滤波的雷达扩展目标TBD算法的有效性。假设目标的运动方程为：

其中，

目标在x-y平面内做匀速直线运动，w_k–1为零均值Gaussian噪声，其协方差Q为：

其中，q₁和q₂分别表示运动和强度的过程噪声方差。设置q₁=0.001, q₂=0.01, q₃=0.01设置T为1 s。其他相关参数设置为D_x=D_y=1, ${\Large\varSigma} = 0.9$ , ${N_\rm{r}} = {N_\rm{a}} = 20$ , ${\alpha _{m}} = 0.3$ ，观测噪声方差为 ${\sigma ^2} = 1$ 。取 ${{x}_\rm{1}} = {\left[ {\begin{array}{*{20}{c}}0&1&2&0&I\end{array}} \right]^\rm{T}}$ ，在整个跟踪过程中，共有32帧。其中，第7到25帧时E_k=1，共19帧，而杂波和噪声从第1帧到第32帧一直存在。信杂噪比计算公式为：

其中，S为信号功率，C为杂波功率，V为噪声功率。

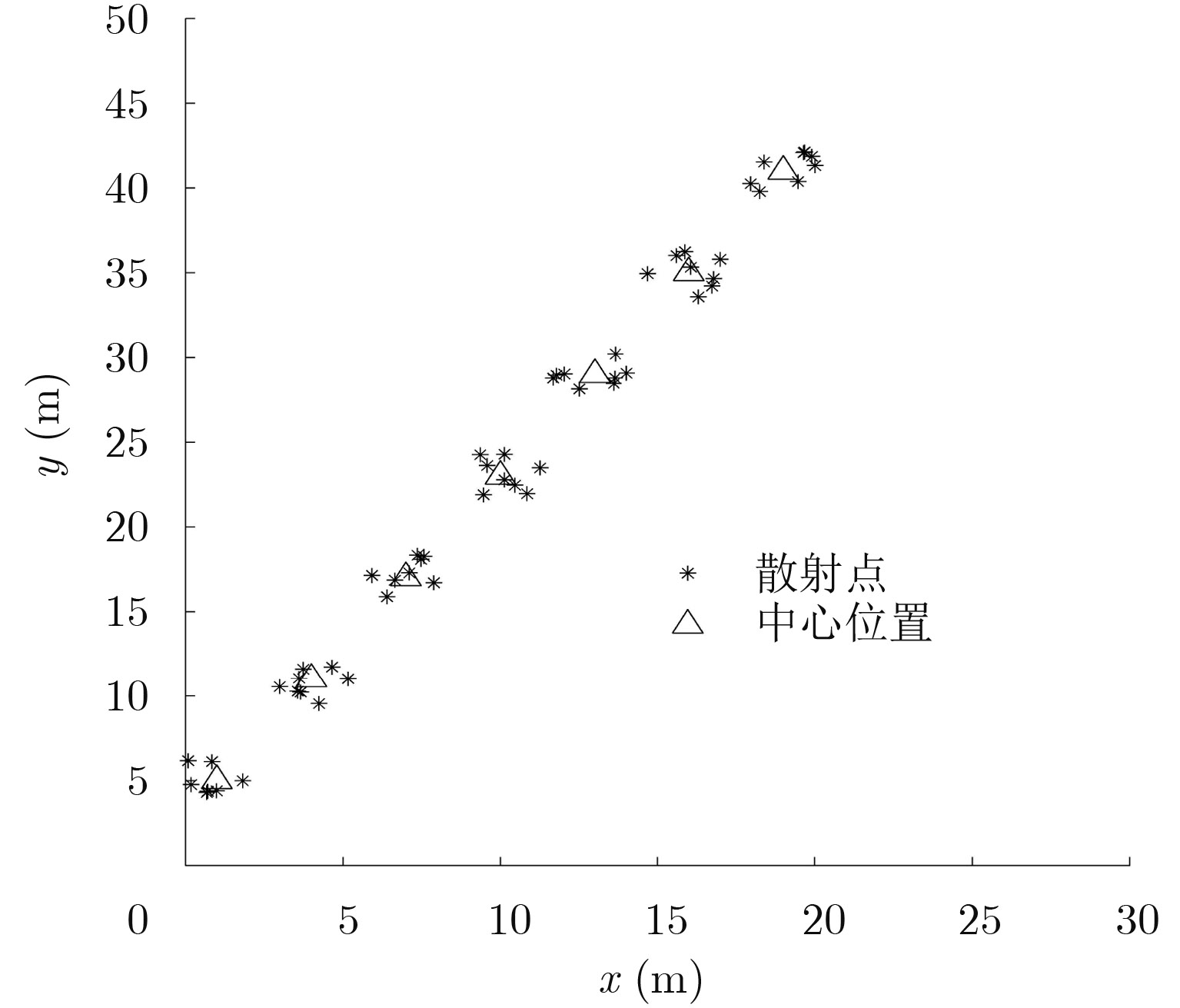
图1模拟了散射点模型。根据散射点状态可知，从状态点到扩散点满足均匀分布。在图中，为了清楚地体现扩散效果，围绕着中心点取了8个扩散点。

图 1(Fig. 1)

图 1 目标散射点 Fig.1 Target scatter point

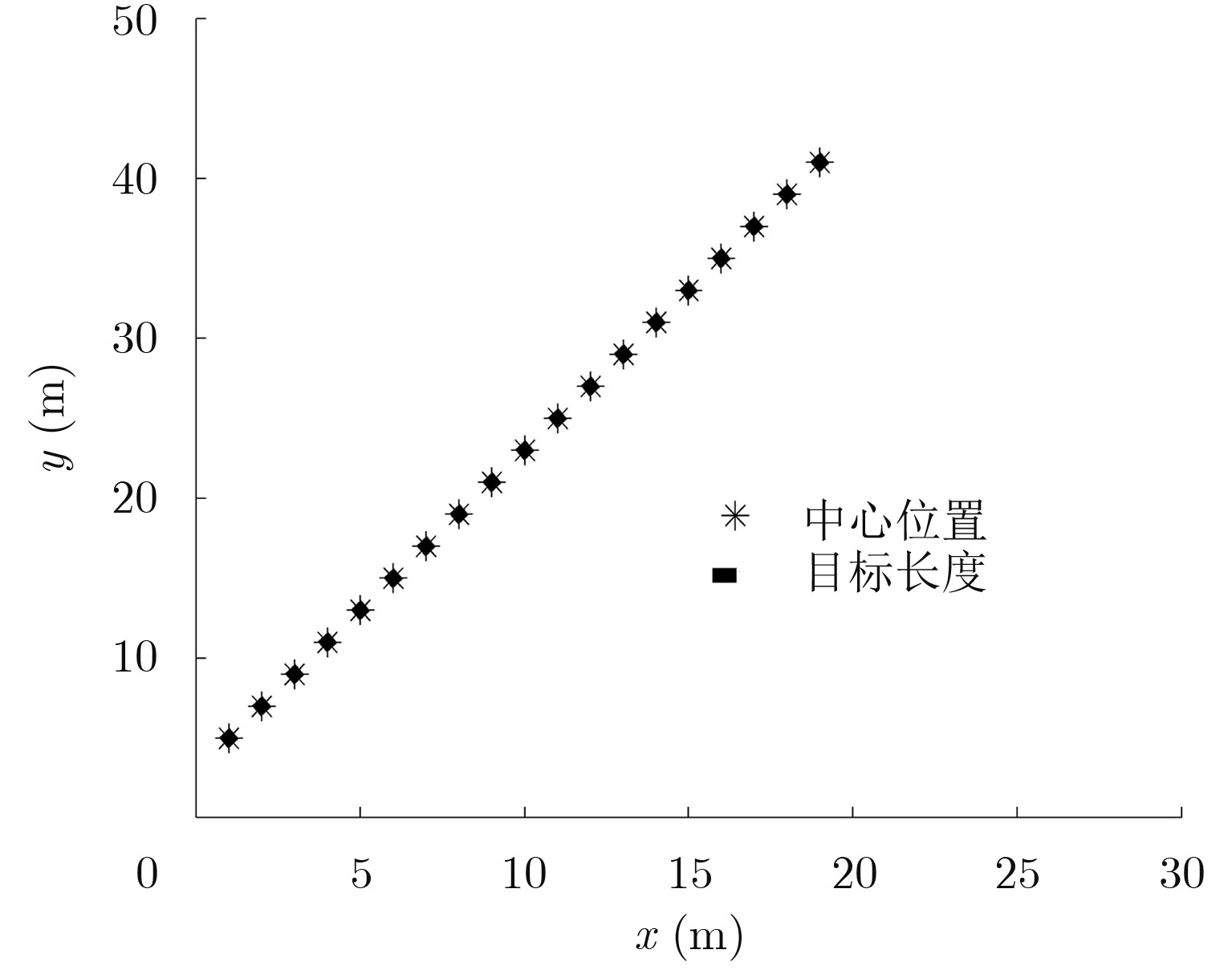
图2给出了扩展目标在x-y平面上的运动轨迹，其中x轴、y轴只是相对值。在整个过程中，目标做匀速直线运动。目标的初始位置为(10, 2)，设设杆长l为2，即占据2个分辨率单元。

图 2(Fig. 2)

图 2 扩展目标真实航迹图 Fig.2 Real track of extended target

滤波参数设置为：目标的p_b和p_d都取为0.1，初始存在概率 ${\mu _1}$ =0.05，信号强度门限 $\gamma $ =0.5, v_max=1, I_min=5, I_max=50, p=2。

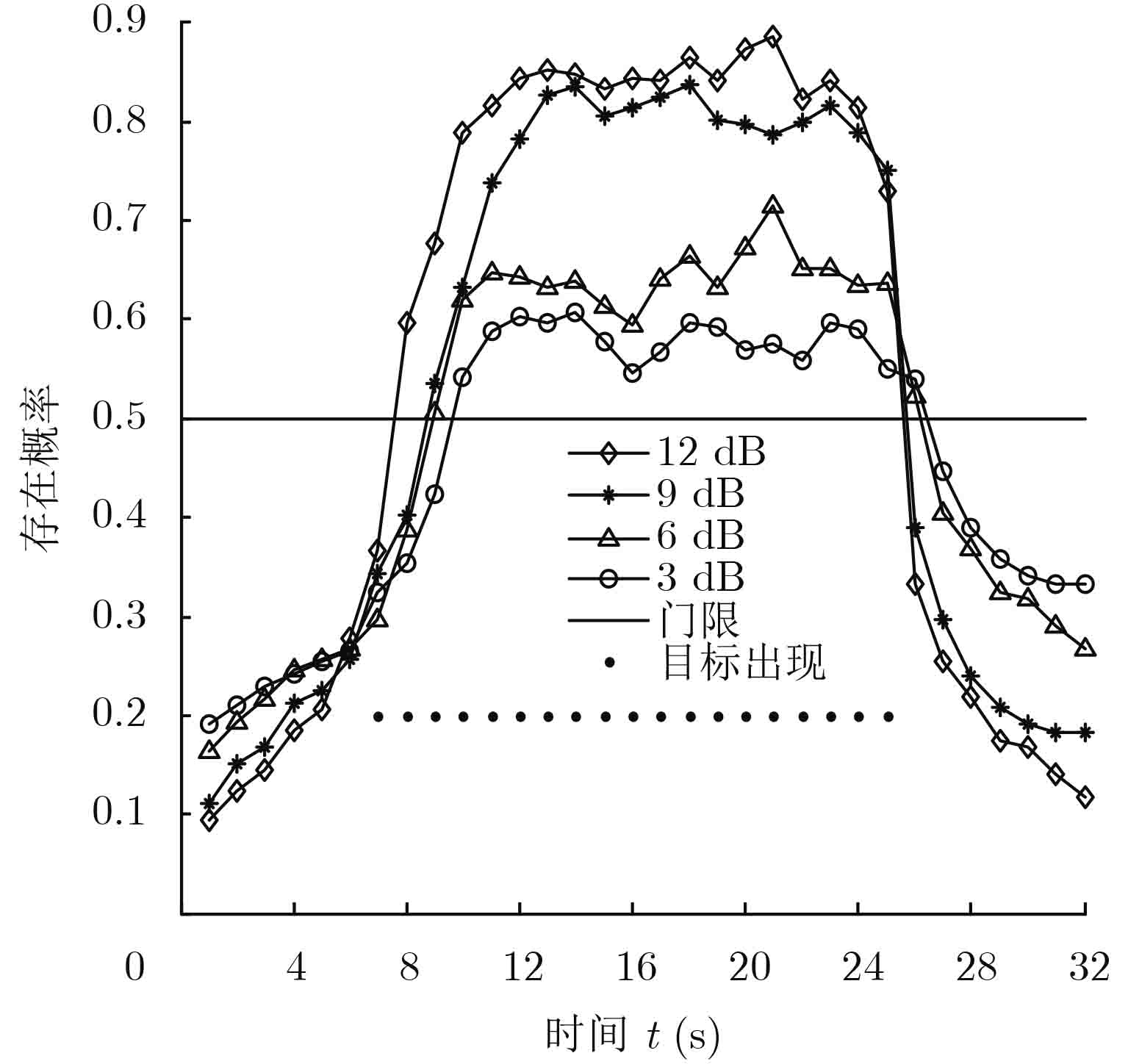
图3是不同SCNR下扩展目标的平均存在概率图，设置门限为0.5，即目标的平均概率超过0.5，认为能够检测到目标，否则相反。从整体上来看，SCNR=3 dB, 6 dB, 9 dB和12 dB均能够检测到目标存在。SCNR=12 dB能够准确检测出目标出现时刻和消失时刻。SCNR=9 dB在目标出现时有2个时刻延迟，但能够准确检测到目标消失时刻。SCNR=3 dB, 6 dB时在目标出现时有2个时刻延迟，而目标消失时刻则有1个延时。

图 3(Fig. 3)

图 3 目标的平均存在概率 Fig.3 Average existence probability of target

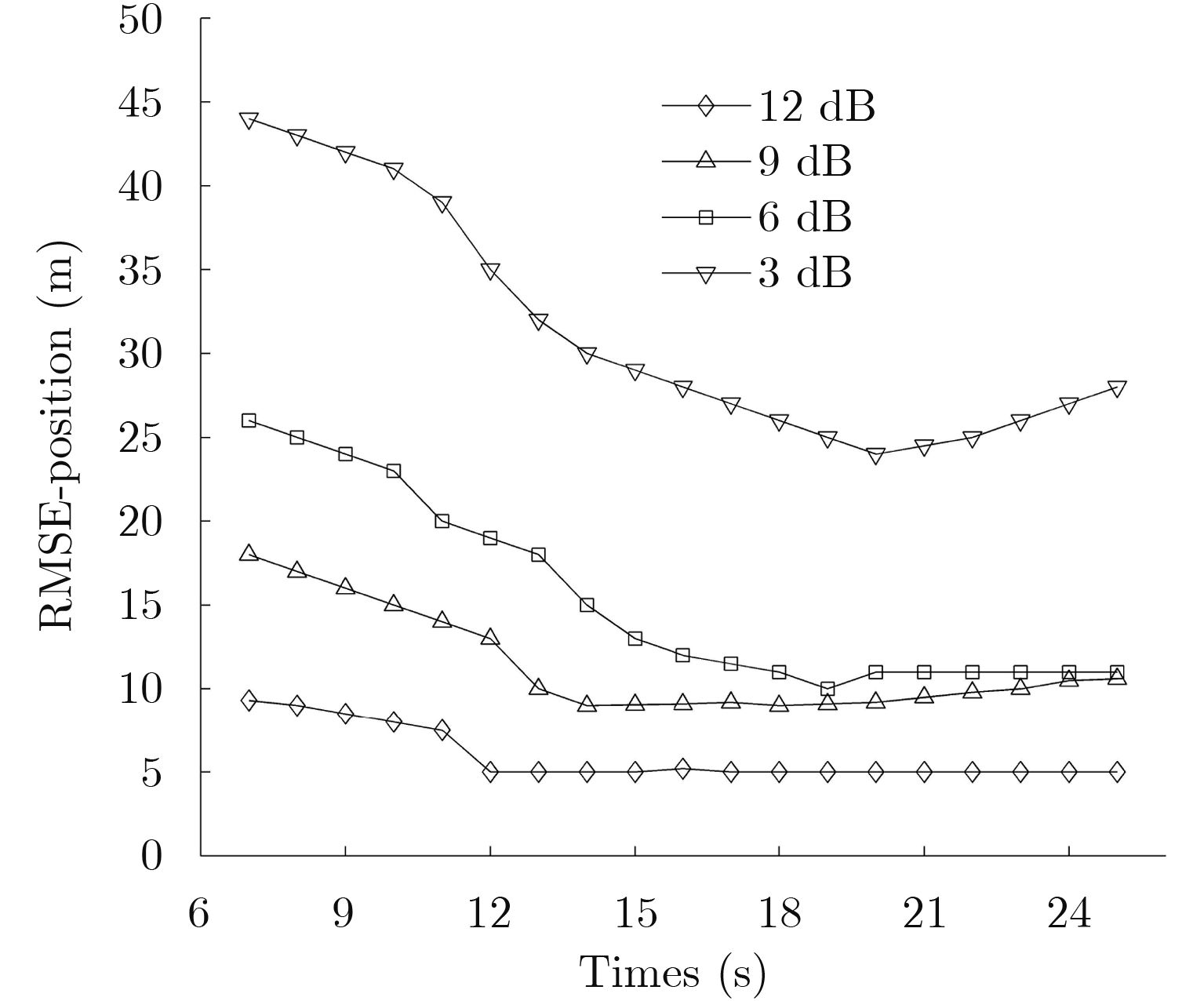
从图4可以看出，在目标开始出现时，不同SCNR下，误差都比较大，但经过几个时刻后，误差趋于稳定，但仍有一些波动。比较这4种不同情况，SCNR=3 dB的误差最大，这是比较符合实际情况。

图 4(Fig. 4)

图 4 目标位置的RMSE Fig.4 RMSE of target position

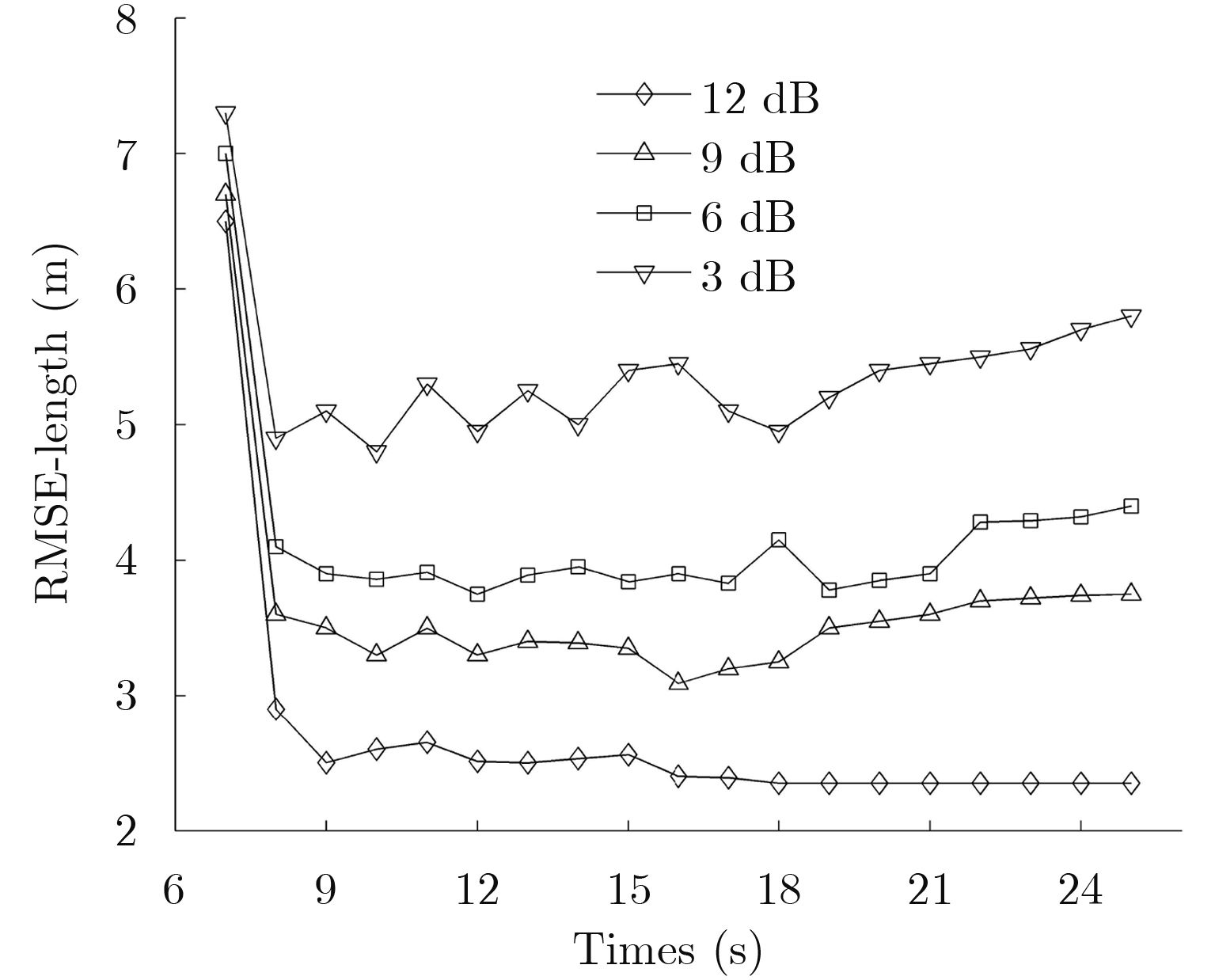
图5是目标长度的随时间变化的RMSE，从图中可以看出，目标刚出现时，误差比较大，随着时间的积累，误差逐渐减少。比较不同SCNR下的误差值，可以得出，SCNR=12 dB时，误差最小，也比较平缓，SCNR=3 dB估计值不太理想，误差一直居高不小。SCNR=6 dB和SCNR=9 dB时，误差均可以接受。

图 5(Fig. 5)

图 5 目标长度的RMSE Fig.5 RMSE of target length

针对杂波环境下的雷达扩展目标检测前跟踪问题，采用了含有Weibull杂波分布的杆状量测模型，运用散射点函数，推导出扩展目标的似然函数和粒子权重。基于粒子滤波，抽样得到散射点集合。实验结果表明，Weibull杂波环境下PF-TBD算法具有较好的稳定性。