海杂波背景下的自适应检测问题因其重要的战略意义和民用价值,一直以来备受国内外学者的关注。常见的自适应检测算法[1,2]中,其实现过程首先要对待检测单元的杂波协方差矩阵进行估计。因此,根据不同协方差矩阵估计方法得到的估计结果会对雷达目标检测性能产生重要影响。
在实际目标检测中,我们可以利用与待检测单元相邻的参考单元实现协方差矩阵的估计。其中,最大似然(Maximum Likelihood, ML)估计方法[3,4]具有很高的估计精度,但是计算复杂度极大;此外,相关学者对传统的采样协方差矩阵(Sample Covariance Matrix, SCM)估计方法进行改进,将其杂波功率进行归一化处理,提出了性能更稳定的归一化样本协方差矩阵(Normalized Sample Covariance Matrix, NSCM)[5]估计方法,该方法大大降低了运算复杂度,但在应用于检测器时无法关于NSCM保持恒虚警率(Constant False Alarm Rate, CFAR)[6,7],进而影响检测性能。针对以上问题,文献[8]中提出了近似最大似然(Approximate Maximum Likelihood, AML)估计方法,该方法不仅可以保证较理想的估计精度和计算复杂度,还可以保证自适应检测器所要求的CFAR。
不同协方差矩阵估计方法的估计性能通常采用归一化F范数[9]来评价。该方法利用杂波协方差矩阵的真实值与估计值之间的相对误差检验估计精度,但考虑实际雷达目标检测中很难得知杂波协方差矩阵真实值的大小,进而导致该方法在实际应用中具有一定局限性。为了解决传统评价方法存在的弊端,该文提出一种用于检验散斑协方差矩阵估计性能的白化度评价方法,该方法利用散斑协方差矩阵在雷达系统白化滤波过程中的去相关作用,通过计算白化滤波后的杂波向量中脉冲间的相关程度来评价散斑协方差矩阵估计方法的估计误差大小。实验结果显示,白化度评价方法与传统的归一化F范数评价方法的结果相一致,同时该方法不依赖杂波协方差矩阵的真实值大小,有效的避免了传统评价方法在实测数据处理中的局限性。
本文其余部分安排如下,第2节对几种类型的杂波协方差矩阵估计方法进行简要介绍和比较;第3节首先概括传统的归一化F范数评价方法,随后介绍白化度评价方法的定义和性质;第4节分别通过仿真实验和实测数据验证白化度评价方法的有效性;第5节总结全文。
2 协方差矩阵估计方法判断回波信号r中是否含有目标信号s等价于下式的二元假设检验问题:
| $\left. {\begin{array}{*{20}{c}}\!\!\!\!\!\!\!\!\!\!{{{\rm H}_0}:{{r}}= {{z}}, {{{r}}_k} = {{{z}}_k}, \;\; k = 1,2, \cdots ,N}\\{{{\rm H}_1}:{{r}} = {{s}} + {{z}}, {{{r}}_k} = {{{z}}_k}, \;\; k = 1,2, \cdots ,N}\end{array}} \right\}$ | (1) |
其中,z表示杂波向量。复合高斯模型下的l维海杂波向量可以表示为两个相互独立的变量的乘积[10,11],即
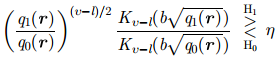
|
(2) |
式中,变量
考虑到实际雷达检测环境中有海尖峰的存在,此时海杂波的功率起伏较大,从而导致传统的样本协方差矩阵(Sample Covariance Matrix, SCM)估计性能不稳定。对此,文献[15]中将其功率进行归一化处理,提出了一种归一化样本协方差矩阵(Normalized Sample Covariance Matrix, NSCM)估计方法,其估计值
| ${\hat {{M}}_{\rm NSCM}} = \frac{1}{N}\sum\limits_{k = 1}^N {\left( {\frac{m}{{{z}_k^{\rm H}{{{z}}_k}}}} \right){{{z}}_k}{{z}}_k^{\rm H}} $ | (3) |
式中
NSCM估计方法虽然解决了杂波功率起伏的影响,且计算复杂度较低,但在应用于广义似然比检测器时,其结果对于杂波的协方差矩阵无法保证恒虚警,影响检测性能。
2.2 最大似然估计方法最大似然估计方法[17]利用包含研究变量的似然函数,对该变量求偏导从而得到使似然函数最大的对应变量值。为此,定义似然函数为N组独立同分布的杂波向量的联合概率密度函数,其表达式如下:
| $\! {p_{{z}}}({{{z}}_1},{{{z}}_2}, \cdots ,{{{z}}_N}) \!\!=\! {{π} ^{ - Nm}}\!{\left| {{M}} \right|^{ - N}}\!\mathop \prod \limits_{k = 1}^N h({{z}}_k^{\rm H}{{{M}}^{ - 1}}\!{{z}_k})$ | (4) |
其中,hm
为了得到散斑协方差矩阵M的最大似然估计值
| ${\hat {{M}}_{\rm ML}}(i + 1) = \sum\limits_{k = 1}^N {\frac{1}{N}{c_m}({{z}}_k^{\rm H}\hat {{M}}_{\rm ML}^{ - 1}(i){{\rm {z}}_k}) \cdot {{\rm {z}}_k}{\rm {z}}_k^{\rm H}} $ | (5) |
其中,
通常最大似然估计方法估计精度较其他估计方法要高,实际研究中相关学者利用式(5)的迭代形式解决了超越方程的无法求解的问题,但也使该方法的计算复杂度大大增加,严重影响雷达的工作效率。
2.3 近似最大似然估计方法近似最大似然(Approximated Maximum Likelihood, AML)估计方法[8]针对上述两种估计方法的问题,采用两步一对一最大化的方法,分别对协方差矩阵M及纹理
| ${\hat {{M}}_{\rm AML}}(i + 1) = \sum\limits_{k = 1}^N {\frac{1}{N}{d_m}({{z}}_k^{\rm H}\hat {{M}}_{\rm AML}^{ - 1}(i){{{z}}_k}) \cdot {{{z}}_k}{{z}}_k^{\rm H}} $ | (6) |
式中
需要说明的是,式(5)及式(6)两种估计方法的求解均需已知初始矩阵
针对上述几种协方差矩阵估计方法,需要寻找合适的性能评价方法来比较不同检测环境中各估计结果的误差大小,确保在实际雷达工作中选择最优的估计方法,提高检测性能。
3.1 归一化F范数归一化F范数检验作为传统的估计性能评价方法,其主要思想是利用蒙特卡洛方法计算杂波协方差矩阵估计值
|
ε
| (7) |
其中
观察式(7)可知,该检验方法在实现性能评价时需已知真实协方差矩阵M的大小。考虑到在实际雷达的数据处理中,矩阵M值通常无法得知,此时利用归一化F范数检验方法则无法实现对协方差矩阵估计性能的评价。
3.2 白化度评价为了在杂波协方差矩阵真实值M未知的情况下实现对其估计性能的检验,本文提出了一种适用于实际数据在独立同分布环境中的白化度评价方法。
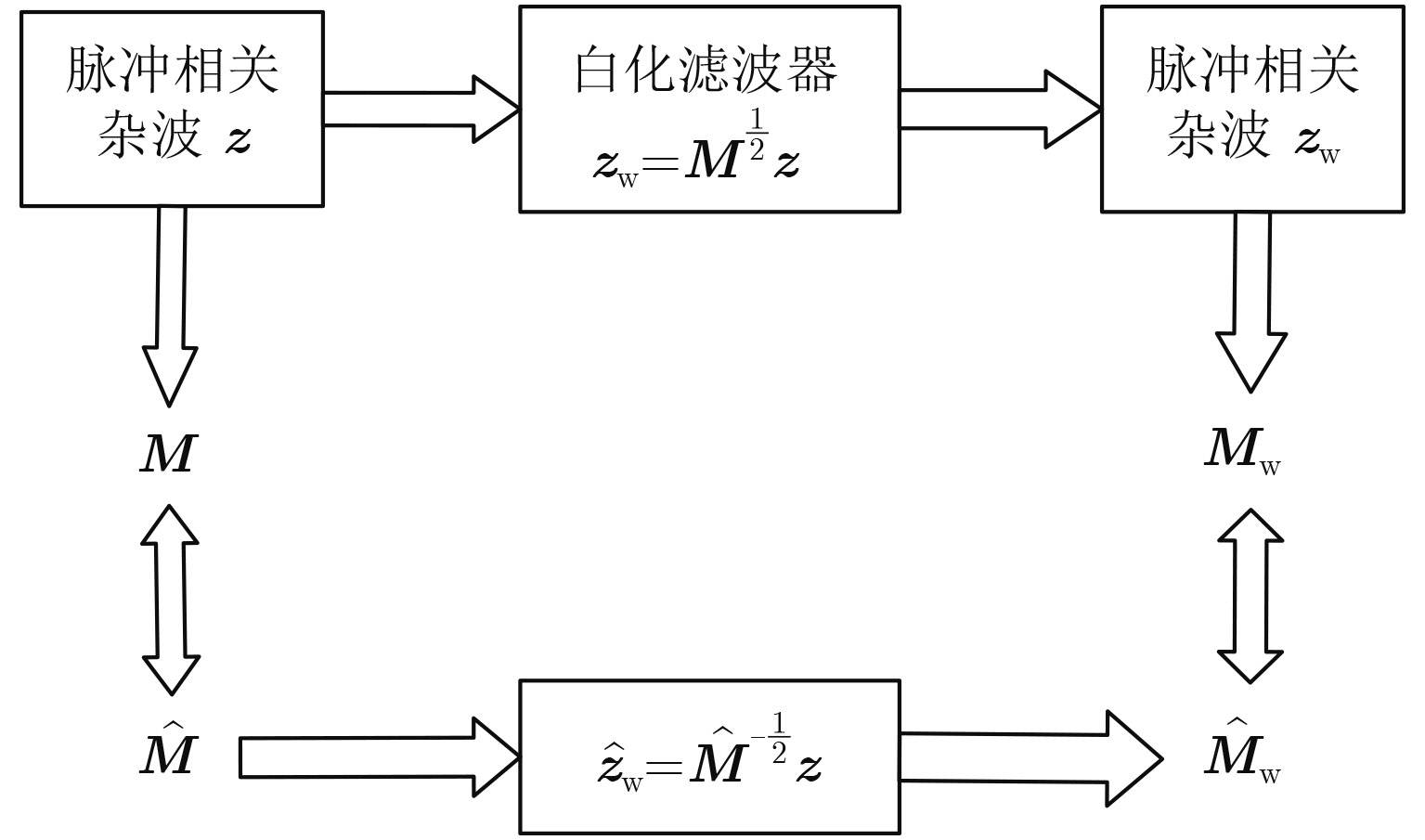
白化度评价方法来源于雷达目标检测中的白化滤波处理过程,其结构示意图如图1所示。雷达在白化滤波处理中利用杂波的协方差矩阵去除脉冲间的相关性,以便于后续模块中对回波的分离处理及分析,而杂波的协方差矩阵就代表杂波向量中脉冲之间的相关程度。利用真实杂波协方差矩阵M对杂波序列z进行白化处理时,可以完全去除脉冲间的相关性,此时得到白化回波
|
图 1 白化度评价结构示意图 Fig.1 Structural representation of WD evaluation |
首先利用杂波协方差矩阵的估计值
| ${\hat {{z}}_{\rm w}} = {\hat {{M}}^{ - \frac{1}{2}}}{{z}}$ | (8) |
式中,
| ${\hat {{M}}_{\rm w}} = \frac{1}{N}\sum\limits_{k = 1}^N {{{\hat {{z}}}_{{{\rm w}_k}}}\hat {{z}}_{{{\rm w}_k}}^{\rm H}} $ | (9) |
其中,
为了利用数值表示出白化杂波估计值
| ${{P}_{\text{w}}}=\frac{\sum\limits_{j=1}^{l}{\sum\limits_{i=1,i\ne j}^{l}{{{\left| {{{\hat{M}}}_{\text{w}}} \right|}_{i,j}}}}}{\text{Tr}\left\{ {{{\hat{M}}}_{\text{w}}} \right\}}\times \frac{1}{l-1}$ | (10) |
式中,
定义协方差矩阵M的元素满足
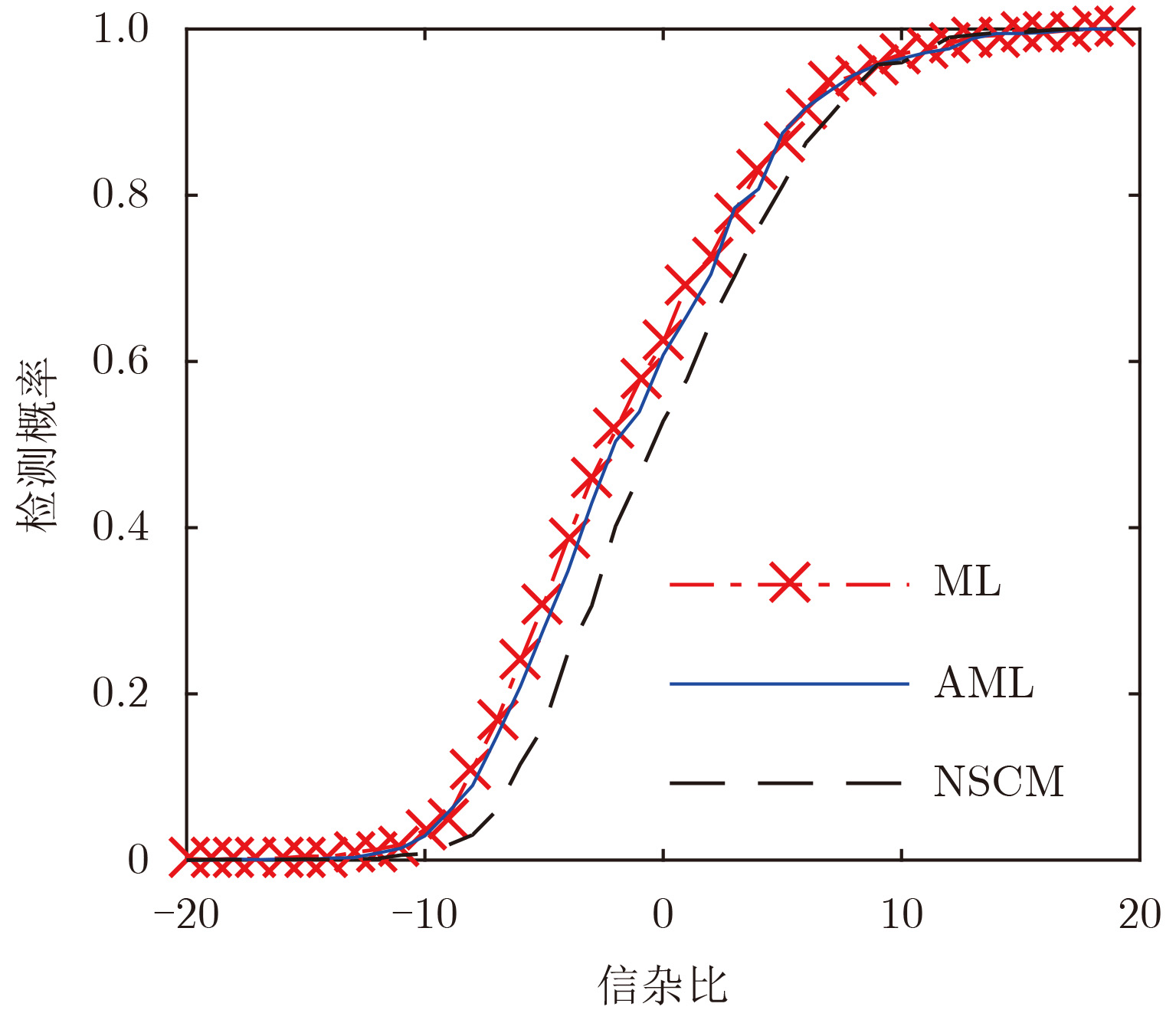
已知相同检测环境下,协方差矩阵估计误差越小,对应检测器的检测概率越大,因此图2对应实验中设定纹理的形状参数为0.5,尺度参数为1,利用式(2)表示的OKD检测器对该仿真数据下的信号进行检测。考虑实际雷达检测中杂波相关系数
|
图 2 3种估计方法的检测概率曲线 Fig.2 Detection probability curves of different estimators |
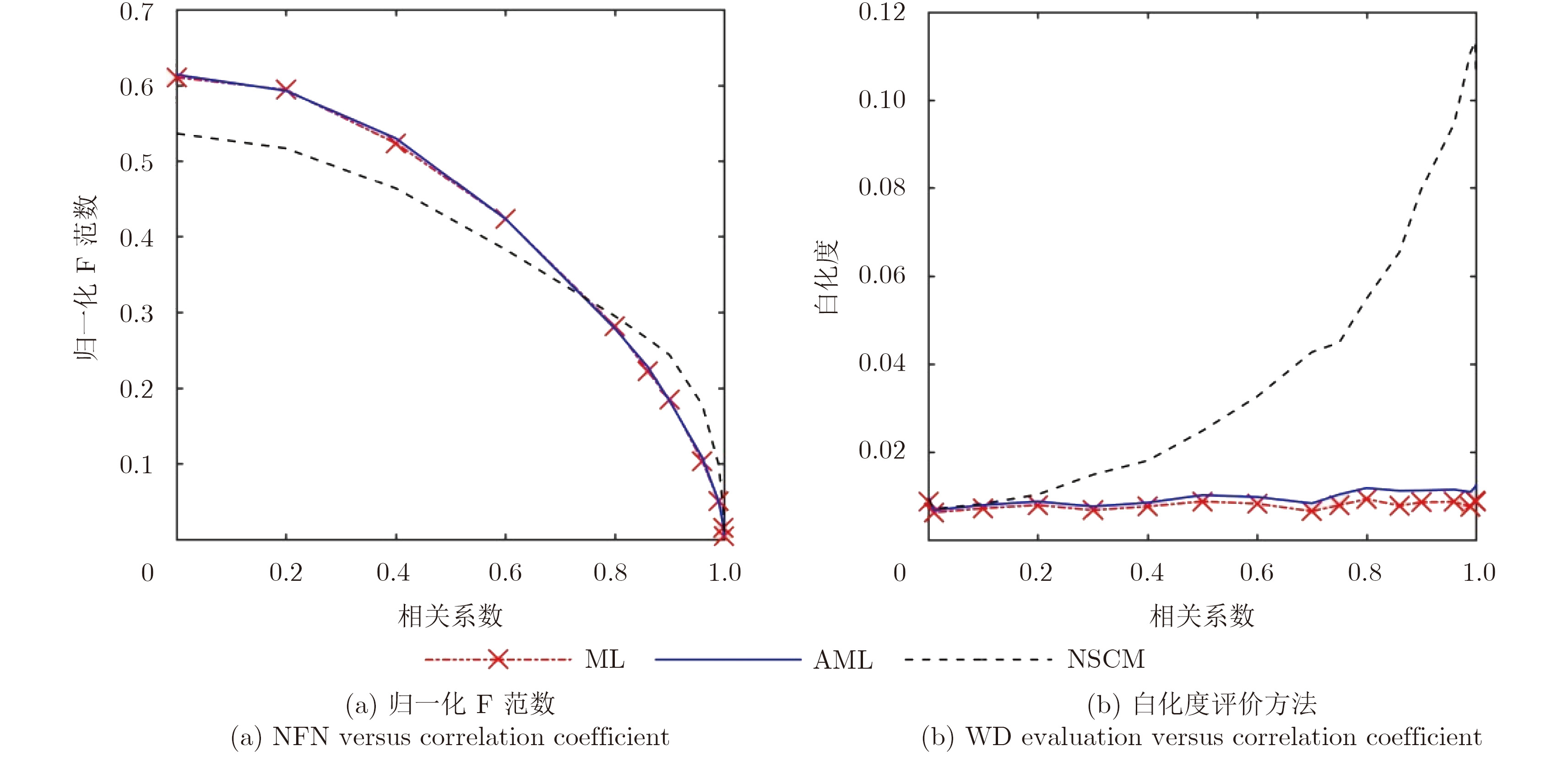
相比于图2的检测概率结果,图3中对应相关系数
|
图 3 归一化F范数及白化度评价方法的性能对比 Fig.3 Performance comparison between NFN and WD evaluation |
利用南非X-波段实测数据(TFC15_001.mat~TFC15_019.mat)验证白化度评价方法对协方差矩阵估计性能评价结果与检测概率一致。
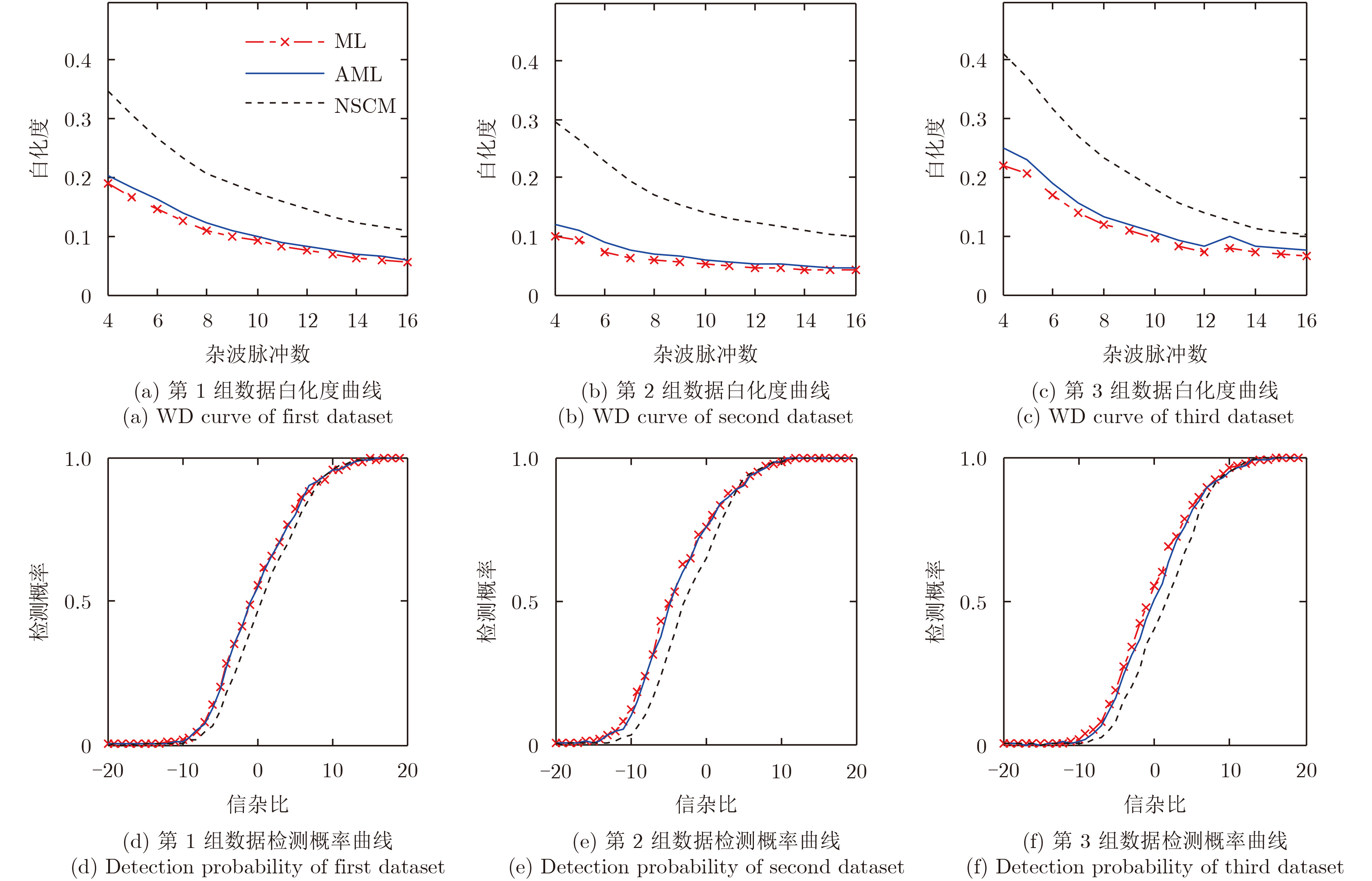
首先随机选取其中3组数据,TFC15_001.mat, TFC15_005.mat及TFC15_007.mat,分别计算出白化度及检测概率的对应曲线,如图4。其中,图4(a)~图4(c)中设定参考单元数N=2l, l为杂波脉冲数从4到16遍历取值,得到3组数据的白化度随脉冲数的变化曲线,可见所有曲线除满足随着脉冲数增加白化度值降低之外,都符合ML估计性能优于AML估计,NSCM估计最差的规律。另设定脉冲数为8,依次得到3组数据的检测概率随信杂比的变化曲线,如图4(d)~图4(f)所示。观察可知,3组曲线均满足ML估计检测概率最高,AML估计次之,NSCM最差,即对于同组数据检测概率的结果与图4(a)~图4(c)中白化度评价结果对应一致。
|
图 4 3组实测数据的白化度及检测概率对比曲线 Fig.4 WD and detection probability of different datasets |
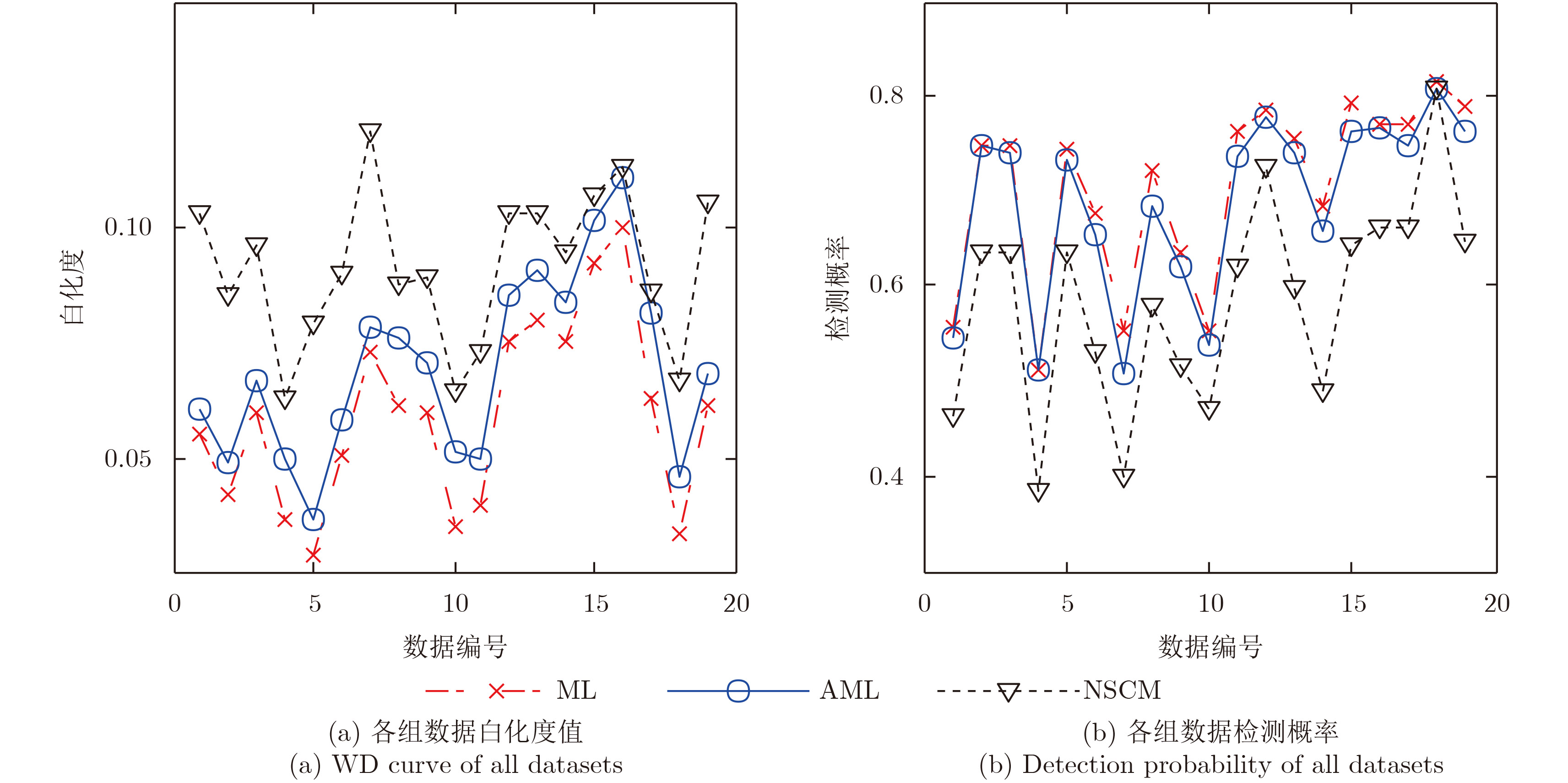
为更直观验证上述结论,图5(a)选定杂波脉冲数为8得出全部19组数据的白化度值,并计算信杂比为0 dB时各组数据对应的检测概率如图5(b)所示。观察可知,各组数据均满足白化度值越小,对应的估计方法的检测概率越大,即针对于实测数据,本文介绍的白化度评价方法的性能检测结果与检测器结果一致。
|
图 5 19组数据白化度及检测概率对比图 Fig.5 WD and detection probability of all datasets |
本文介绍了雷达自适应检测中的几种协方差矩阵估计方法并分析了其优缺点。考虑到归一化F范数作为传统协方差矩阵估计误差的评价方法存在必须已知真实协方差矩阵值的缺陷,本文提出一种白化度评价方法实现对估计误差的检验。实验结果表明,该评价方法在实际雷达检测中具有检验结果的一致性并且有效的避免了传统的估计性能检验方法在实测数据处理中的局限性。
| [1] |
Conte E and Longo M. Characterisation of radar clutter as a spherically invariant random process[J].
IEE Proceedings F-Communications, Radar and Signal Processing, 1987, 134(2): 191-197.DOI:10.1049/ip-f-1:19870035( 0) 0)
|
| [2] |
Rangaswamy M, Weiner D D and Ozturk A. Non-Gaussian random vector identification using spherically invariant random processes[J].
IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(1): 111-124.DOI:10.1109/7.249117( 0) 0)
|
| [3] |
Pulsone N B. Adaptive signal detection in non-Gaussian interference[D]. [Ph.D. dissertation], Northeastern University, 1997.
( 0) 0)
|
| [4] |
Raghavan R S and Pulsone N B. A generalization of the adaptive matched filter receiver for array detection in a class of non-Gaussian interference[C]. Proceedings of the Adaptive Sensor Array Processing (ASAP) Workshop, Lexington, MA, USA, Mar. 1996: 499–517.
( 0) 0)
|
| [5] |
Conte E, Lops E, and Ricci G. Adaptive radar detection in compound-Gaussian clutter[C]. Proceedings of the European Signal Processing Conference, Edinburgh, Scotland, UK, Sep. 1994.
( 0) 0)
|
| [6] |
何友, 简涛, 苏峰, 等. 非高斯杂波协方差矩阵估计方法及CFAR特性分析[J].
中国科学: 信息科学, 2011, 41(1): 90-99. He You, Jian Tao, Su Feng, et al..CFAR assessment of covariance matrix estimators for non-Gaussian clutter[J]. Scientia Sinica (Informationis), 2011, 41(1): 90-99.(  0) 0)
|
| [7] |
孙艳丽, 谢宁波. 基于实测数据的单元平均CFAR检测器性能分析[J].
兵器装备工程学报, 2016, 37(10): 84-87. Sun Yan-li and Xie Ning-bo. Performance analysis of cell average CFAR detector based on measured data[J]. Journal of Sichuan Ordnance, 2016, 37(10): 84-87.DOI:10.11809/scbgxb2016.10.017(  0) 0)
|
| [8] |
Gini F and Greco M. Covariance matrix estimation for CFAR detection in correlated heavy tailed clutter[J].
Signal Processing, 2002, 82(12): 1847-1859.DOI:10.1016/S0165-1684(02)00315-8( 0) 0)
|
| [9] |
Pascal F, Chitour Y, Ovarlez J P, et al..Covariance structure maximum-likelihood estimates in compound Gaussian noise: existence and algorithm analysis[J].
IEEE Transactions on Signal Processing, 2008, 56(1): 34-48.DOI:10.1109/TSP.2007.901652( 0) 0)
|
| [10] |
Anastassopoulos V, Lampropoulos G A, Drosopoulos A, et al..High resolution radar clutter statistics[J].
IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 43-60.DOI:10.1109/7.745679( 0) 0)
|
| [11] |
Ward K D, Baker C J and Watts S. Maritime surveillance radar. I. radar scattering from the ocean surface[J].
IEE Proceedings F-Radar and Signal Processing, 1990, 137(2): 51-62.DOI:10.1049/ip-f-2.1990.0009( 0) 0)
|
| [12] |
Zhou Jie, Chen Dong, and Sun Dewei. K distribution sea clutter modeling and simulation based on ZMNL[C]. Proceedings of the 2015 8th International Conference on Intelligent Computation Technology and Automation, Nanchang, China, Jun. 2015: 506–509. DOI: 10.1109/ ICICTA.2015.279.
( 0) 0)
|
| [13] |
谢洪森, 邹鲲, 杨春英, 等. 海杂波协方差矩阵估计及其对目标检测性能的影响[J].
系统工程与电子技术, 2011, 33(10): 2174-2178. Xie Hong-sen, Zou Kun, Yang Chun-ying, et al..Sea clutter covariance matrix estimation and its impact on signal detection performance[J]. Systems Engineering and Electronics, 2011, 33(10): 2174-2178.DOI:10.3969/j.issn.1001-506X.2011.10.06(  0) 0)
|
| [14] |
Shui Peng-lang, Liu Ming and Xu Shu-wen. Shape-parameter-dependent coherent radar target detection in k-distributed clutter[J].
IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(1): 451-465.DOI:10.1109/TAES.2015.140109( 0) 0)
|
| [15] |
Jansson M and Ottersten B. Structured covariance matrix estimation: A parametric approach[C]. Proceedings of the 2000 IEEE International Acoustics, Speech, and Signal Processing, Istanbul, Turkey, Jun. 2000, 5: 3172–3175.
( 0) 0)
|
| [16] |
Conte E, Lops M and Ricci G. Adaptive detection schemes in compound-Gaussian clutter[J].
IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1058-1069.DOI:10.1109/7.722671( 0) 0)
|
| [17] |
Shui Peng-lang, Shi Li-xiang, Yu Han, et al..Iterative maximum likelihood and outlier-robust bipercentile estimation of parameters of Compound-Gaussian clutter with inverse Gaussian texture[J].
IEEE Signal Processing Letters, 2016, 23(11): 1572-1576.DOI:10.1109/LSP.2016.2605129( 0) 0)
|
| [18] |
宋运忠, 杨丽英. 基于L1范数最小化的逆协方差矩阵估计
[J].
河南师范大学学报(自然科学版), 2016, 44(5): 8-19. Song Yun-zhong and Yang Li-ying. A approach to precision matrix estimation based on L1norm minimization [J]. Journal of Henan Normal University (Natural Science Edition), 2016, 44(5): 8-19.DOI:10.16366/j.cnki.1000-2367.2016.05.002.(  0) 0)
|




