1 引言

多输入多输出(MIMO)雷达作为一种新体制雷达 ^[1] ，目前已受到雷达界学者的广泛关注。MIMO雷达利用多个发射天线发射波形，通过对多个接收天线接收到的信号进行联合处理以提高对目标的探测性能。根据雷达站的空间分布位置，MIMO雷达可以被分为两大类。一类是天线集中式布置的MIMO雷达(colocated MIMO) ^[2] ，另一类是天线分布式布置的MIMO雷达(distributed MIMO) ^[3] 。

根据各通道回波信号的相关性，分布式MIMO雷达又可以分为两种情况：相参MIMO雷达(coherent MIMO)和非相参MIMO雷达(noncoherent MIMO) ^[3] 。前者各传输通道中目标回波表现出相同的特性，接收端能够进行相参处理，利用相参增益提高对目标的探测性能 ^[4] ；后者通过观测某一域上不同维度的目标来进行检测，如波形分集、空间分集和极化分集，利用回波信号的分集增益提高性能 ^[5] 。分集处理可以克服传统相控阵雷达在弱目标，尤其是隐身目标检测方面的不足。

目前，针对MIMO雷达目标检测的研究比较多。文献[ 5]对比了MIMO雷达和相控阵雷达的目标检测性能，并深入研究了目标雷达散射截面(Radar Cross Section, RCS)起伏对雷达检测性能的影响。文献[6]研究了加性高斯白噪声中统计MIMO雷达中的广义似然比检测器(Generalized Likelihood Ratio Test, GLRT)，同时给出了检测概率的闭合表达式。文献[7]研究了频率分集MIMO雷达目标检测性能，并说明了这种分集具有同空间分集类似的效果。

现有的论文都只是单独地分析分布式MIMO雷达在某种形态下的检测性能 ^{[8 , 9]} ，而没有系统地分析分布式MIMO雷达不同形态下的检测性能。本文将从布站间隔与回波的相参性出发，首先给出分布式MIMO雷达的3种形态，接着分别分析分布式MIMO雷达3种形态下的检测性能。由于分布式相参MIMO检测性能很多文献都已讨论 ^{[10 – 12]} ，限于篇幅，本文不再详细讨论，本文的重点将放在相位随机分布式MIMO雷达、幅相随机分布式MIMO雷达这两种非相参MIMO雷达的检测性能分析上。本文最后通过仿真对比了分布式MIMO雷达在不同形态下的检测性能。

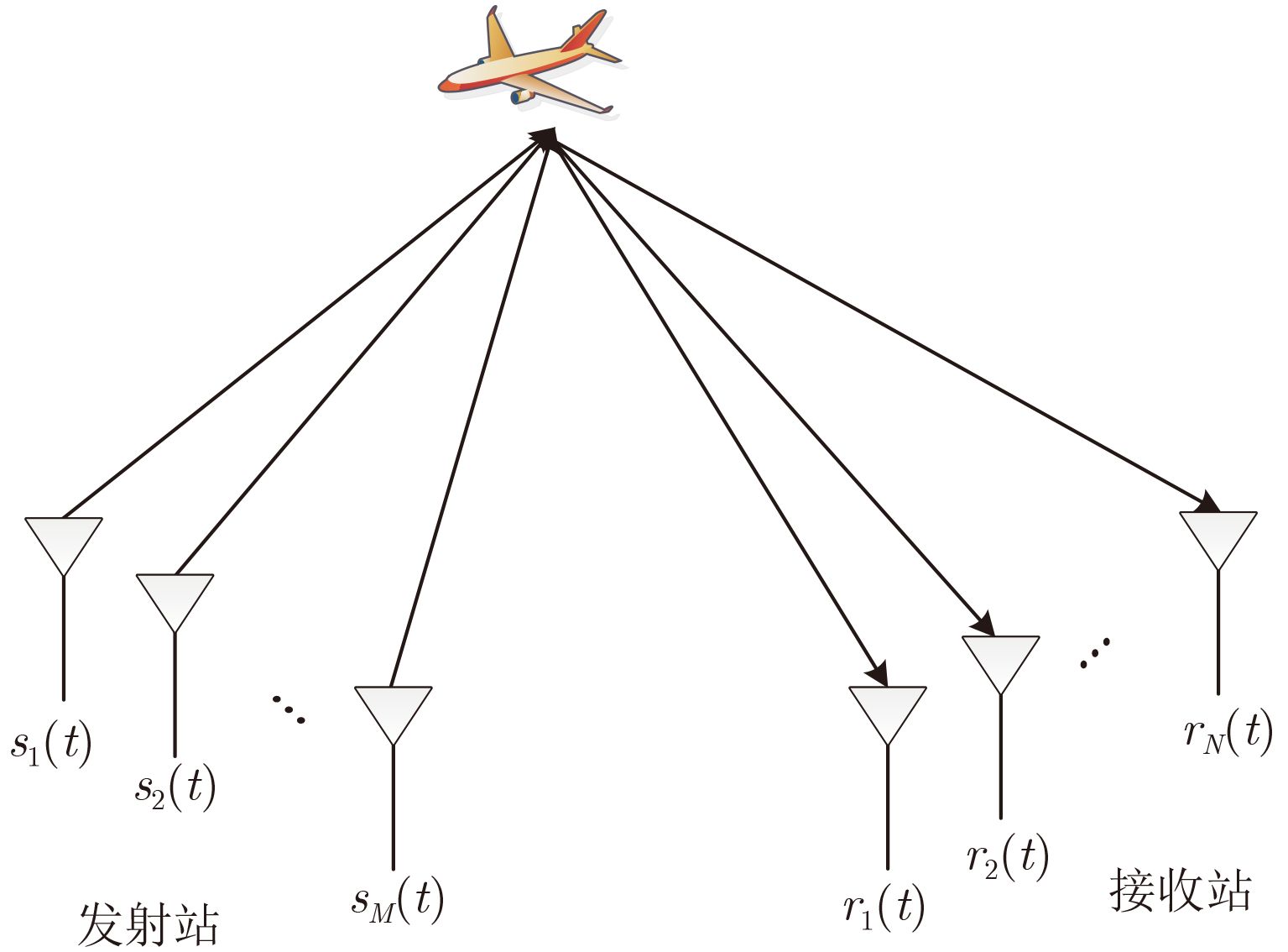
2 分布式MIMO雷达3种形态

本节根据分布式MIMO雷达系统相对于目标的分布场景，如 图1 所示，将分别讨论分布式MIMO雷达的3种形态。分布式MIMO雷达系统的每个收发路径都具有不同且未知的幅度和相位，根据雷达天线的分布位置不同，其形态可以分为3种。

2.1 分布式相参MIMO雷达

当分置MIMO雷达系统各站在空间的位置分布相对集中，即各站之间的间隔满足文献[ 5]中的相参关系，可以认为各站是从同一方向照射与接收目标回波信号，且各站信号是相参发射与接收的，此时，同一个目标的各收发路径的回波表现出相同的散射特性，即，不同路径目标反射系数的幅度相等且相位相同。每条路径的信号回波是相参的。此种场景下，分布式MIMO雷达系统可以看作分布式相参MIMO雷达系统，在发射端和接收端进行相参处理，利用相参增益来提高对目标的检测性能。

分布式MIMO雷达实现全相参后，其检测器结构与传统相控阵雷达一致，此处不再讨论。通过 N 个雷达站的全相参处理，可以带来 N 倍的信噪比改善。

2.2 相位随机分布式MIMO雷达

同2.1小节布站场景相同，即分置MIMO雷达系统各站在空间的位置分布相对集中，各站是近似从同一方向照射与接收目标回波信号，但各站发射与接收信号是非相参的，此时，同一个目标的各收发路径回波表现出相同的幅度特性，但相位是随机的，即可以认为各个路径散射系数的幅度相同，仅散射系数的相位相互独立。通常假设每条路径反射系数的相位服从 $\left( {0,\;2{{π}} } \right)$ 上的均匀分布。

2.3 幅相随机分布式MIMO雷达

下面两种主要场景，将使得分布式MIMO雷达系统各接收路径，对同一个目标的回波RCS幅度和相位都是随机的(无论各站间信号源是否相参)。

(1) 当分布式MIMO雷达系统各站在空间的位置分散，即各站之间的间隔不满足远远小于雷达到目标的距离，可认为各站是从不同方向照射与接收目标回波信号，此时可以认为接收到的各路径回波RCS幅度和相位都是随机的。

(2) 无论分布式MIMO雷达系统各站在空间的位置如何分布，如果各站发射信号间的频率相差较大，即各雷达站发射不同频段的探测信号，此时同一目标对不同频段的探测信号，将呈现不同的RCS，此时，各路径回波RCS幅度和相位也是随机的。

3 相位随机MIMO雷达检测器

本节将详细推导相位随机MIMO雷达检测器结构，并重点分析低信噪比条件下平方律检测器的检测性能。

3.1 检测器结构

不失一般性，假设衰减系数已知，且并入反射系数中。设接收天线数目为 M ，接收天线的数目为 N ，发射信号的总能量为 E 。

接收天线 n 的回波信号模型为：

${r_n}\left( t \right) = \sqrt {\frac{E}{M}} \sum\limits_{m = 1}^M {{\eta _{mn}}{s_m}\left( {t - {\tau _{mn}}} \right)} + {u_n}\left( t \right)$

(1)

式中， ${\eta _{mn}}$ 为第 m 个发射天线到第 n 个接收天线的复散射系数， ${\eta _{mn}} = {\alpha _{mn}}{{\rm e}^{{\rm j}{\beta _{mn}}}}$ , ${\alpha _{mn}}$ 为散射系数的幅度， ${\beta _{mn}}$ 为散射系数的相位。 ${\tau _{mn}}$ 为第 m 个发射天线到第 n 个接收天线的传播延时。 ${u_n}\left( t \right)$ 是均值为0，方差为 $\sigma _n^2$ 的复高斯白噪声。 ${s_m}\left( t \right)$ 为第 m 个发射站发射的信号，发射波形满足正交性 ^[13] ，即

$\int_T {{s_m}\left( t \right)s_{m'}^*\left( t \right)} {\rm d}t = \left\{ {\begin{array}{*{20}{c}}\!\!\!{1,} & {m = m'}\\\!\!\!{0,} & {m \ne m'}\end{array}} \right.$

(2)

对于每个接收天线的接收回波，利用 M 个发射信号分别进行匹配滤波分离出各个路径的信号。称“目标出现在检测单元中”的假设为 H ₁，“没有目标出现”的假设为 H ₀，则在两种假设下，由发射天线 m ( $m = 1, \cdots ,M$ )发射的信号，经接收天线 n ( $n = 1, \cdots ,N$ )接收后的观测值为：

${y_{mn}} = \left\{ \begin{array}{l}\!\!\!\sqrt {\frac{E}{M}} {\alpha _{mn}}{{\rm e}^{{\rm j}{\beta _{mn}}}} + {u_{mn}}, \;\;{H_1}\\\!\!\!{u_{mn}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \quad \;\,{H_0}\end{array} \right.$

(3)

其中， ${u_{mn}} = \int_T^{} {{u_n}\left( t \right)s_m^*\left( t \right)} {\rm d}t$ 为匹配滤波后输出噪声。对于仅相位随机情况，此时，各个散射系数的幅度是相同的，即 ${\alpha _{11}} = {\alpha _{21}} = \cdots = {\alpha _{MN}} = \alpha $ 。 MN 个相位 ${\beta _{11}},{\beta _{21}}, \cdots ,{\beta _{MN}}$ 相互独立，且都服从 $\left( {0,2{{π}} } \right)$ 上的均匀分布。将所有观测值表示成向量的形式为：

${y} = \left[ {{y_{11}}\: \cdots \:\:{y_{M1}}\:{y_{12}}\: \cdots \:\:{y_{mn}}\: \cdots \:\:{y_{MN}}} \right]$

(4)

在 H ₁假设下的联合条件概率密度函数为 ^[14] ：

$\begin{array}{l}{p_1}\!\left( {{y}|{{β}} } \right) \!\!=\!\! \prod\limits_{m = 1}^M\! {\prod\limits_{n = 1}^N \!{\frac{1}{{{{π}} \sigma\!_n\,\!\!^2}}} }\! \exp\! \!\left( \!{ \!-\! \frac{1}{{\sigma _n^2}}\!{{\left| {{y_{mn}} \!-\! \sqrt {\frac{E}{M}} \alpha {{\rm e}^{{\rm j}{\beta _{mn}}}}} \right|}^2}}\!\right)\\\;\;\;\;\;\;\;\;\;\;\;\; = \prod\limits_{m = 1}^M {\prod\limits_{n = 1}^N {\frac{1}{{{{π}} \sigma\! _n\,\!\!^2}}} } \exp\! \left( { - \frac{1}{{\sigma _n^2}}{{\left| {{y_{mn}}} \right|}^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot \exp \left( { - \frac{E}{{M\sigma _n^2}}{\alpha ^2}} \right) \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot \exp \left( {\frac{{2\alpha }}{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|\cos \left( {{\beta _{mn}}\! -\! {\zeta _{mn}}} \right)}\! \right)\end{array}$

(5)

式中， ${\zeta _{mn}}$ 为复观测值 ${y_{mn}}$ 的相位， ${{β}} {\rm{ = }}\left[ {{\beta _{11}}} \quad \right.{\beta _{21}}$ $\left. { \cdots {\beta _{MN}}} \right]$ 。在 MN 个相位上求平均，可得到在假设 H ₁下的联合密度函数为：

$\begin{array}{l}{p_1}\left( {y} \right) = \int_0^{2{{π}} } {{p_1}\left( {{y}|{{β}}} \right)p\left( {{β}} \right){\rm d}{{β}}} \\\;\;\;\;\;\;\;\;\;\; = \prod\limits_{m = 1}^M {\prod\limits_{n = 1}^N {\frac{1}{{{{π}} \sigma _n^2}}} } \exp \left( { - \frac{1}{{\sigma _n^2}}{{\left| {{y_{mn}}} \right|}^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \exp \!\left( \! \!{ - \frac{E}{{M\sigma _n^2}}{\alpha ^2}} \!\right) {I_0}\left( \!{\frac{{2\alpha }}{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|} \!\right)\end{array}$

(6)

式中， ${I_0}( \cdot )$ 为修正的零阶贝塞尔函数，其表达式为：

${I_0}\left( x \right) = \frac{1}{{2{{π}} }}\int_0^{2{{π}} } {{{\rm e}^{x\cos \left( {\beta - \zeta } \right)}}} {\rm d}\beta $

(7)

在 H ₀假设下的联合条件概率密度函数可表示为：

${p_0}\left( {y} \right) = \prod\limits_{m = 1}^M {\prod\limits_{n = 1}^N {\frac{1}{{{{π}} \sigma _n^2}}} } \exp \left( { - \frac{1}{{\sigma _n^2}}{{\left| {{y_{mn}}} \right|}^2}} \right)$

(8)

由式(6)和式(8)可以得到对数似然比函数，

$\ln L\left( {y} \right) = \ln \left( {\frac{{{p_1}\left( {y} \right)}}{{{p_0}\left( {y} \right)}}} \right) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{W_{mn}}} } $

(9)

式中分支判决变量 W _mn 可以表示为：

${W_{mn}} = \ln {I_0}\left( {\frac{{2\alpha }}{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|} \right) - \frac{{E{\alpha ^2}}}{{M\sigma _n^2}}$

(10)

式(10)中的检测器包含了相同的非线性部分，记为 $\ln {I_0}( \cdot )$ 。非线性的性能相当好，但实际很少能够实现，工程中常采用一种折中的方法 ^[15] ：

(1) 当 x 很小时，则有 $\ln {I_0}(x) \approx {x^2}/4$ ，故称为“低信噪比”平方律处理检测器；

(2) 当 x 很大时，则有 $\ln {I_0}(x) \approx x$ ，故称为“高信噪比”线性处理检测器。

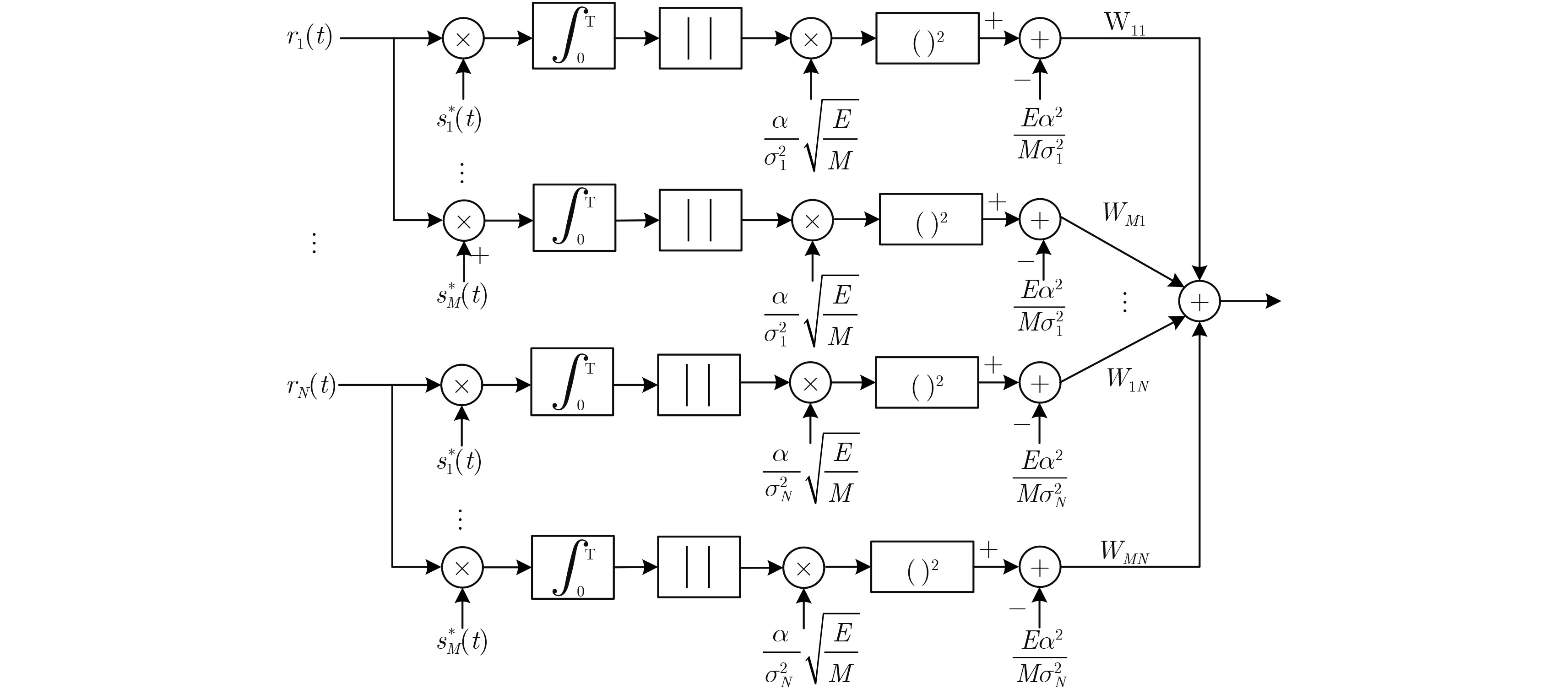
限于篇幅，本文仅讨论低信噪比情况下的处理方法，于是，相位随机MIMO雷达的平方律检测器的结构如 图2 所示，图2给出检测统计量式(9)的检测器结构。

3.2 检测器性能分析

在低信噪比条件下， $\ln {I_0}(x) \approx {x^2}/4$ ，因此，式(10)可以近似为：

${W_{mn}} = {\left( {\frac{\alpha }{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|} \right)^2} - \frac{{E{\alpha ^2}}}{{M\sigma _n^2}}$

(11)

在 H ₁假设下，由于 y _mn 是复高斯随机变量，其均值为 $E\left\{ {{y_{mn}}} \right\} = \sqrt {E/M} \alpha {{\rm{e}}^{{\rm{j}}{\beta _{mn}}}}$ ，方差为 $V\left\{ {{y_{mn}}} \right\} = $ $ \sigma _n^2$ 。

且令 $\left| {{y_{mn}}} \right| = \sqrt {{{\left( {\Re \left\{ {{y_{mn}}} \right\}} \right)}^2} + {{\left( {\Im \left\{ {{y_{mn}}} \right\}} \right)}^2}} $ ，复高斯分布的模服从莱斯分布，且有

$p\left( {\left| {{y_{mn}}} \right|} \right) = \frac{{\left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}\exp \left( { - \frac{{{{\left| {{y_{mn}}} \right|}^2} + E{\alpha ^2}/M}}{{2\sigma _n^2/2}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot {I_0}\left( {\frac{{\sqrt {E/M} \alpha \left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}} \right)$

(12)

令 ${T_{mn}} = {\left( {\displaystyle\frac{\alpha }{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|} \right)^2}$ ，则有

$\left| {{y_{mn}}} \right| = \frac{{\sigma _n^2}}{{\alpha \sqrt {E/M} }}\sqrt {{T_{mn}}} $

(13)

且

${\rm d}{T_{mn}} = 2{\left( {\frac{\alpha }{{\sigma _n^2}}\sqrt {\frac{E}{M}} } \right)^2}\left| {{y_{mn}}} \right|{\rm d}\left| {{y_{mn}}} \right|$

(14)

也即

$\left| {{y_{mn}}} \right|{\rm d}\left| {{y_{mn}}} \right| = \frac{{\sigma _n^4}}{{2{\alpha ^2}E/M}}{\rm d}{T_{mn}}$

(15)

继而可得 T _mn 的概率密度函数为：

$\begin{array}{l}p\left( {{T_{mn}}} \right) = \frac{{\sigma _n^4}}{{2{\alpha ^2}E/M}}\frac{1}{{\sigma _n^2/2}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \exp \left( { - \frac{{{{\left( \Large{\frac{{\sigma _n^2}}{{\alpha \sqrt {E/M} }}}\Large \right)}^2}{T_{mn}} + E{\alpha ^2}/M}}{{\sigma _n^2}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot {I_0}\left( {\displaystyle\frac{{\sqrt {\displaystyle\frac{E}{M}} \alpha \displaystyle\frac{{\sigma _n^2}}{{\alpha \sqrt {E/M} }}\sqrt {{T_{mn}}} }}{{\sigma _n^2/2}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{\sigma _n^2}}{{{\alpha ^2}E/M}}\exp \left( { - \frac{{\sigma _n^2{T_{mn}}}}{{{\alpha ^2}E/M}} - \frac{{E{\alpha ^2}/M}}{{\sigma _n^2}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot {I_0}\left( {2\sqrt {{T_{mn}}} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;=\! \frac{1}{{2s_{mn}^2}}\exp \!\left(\! { -\! \frac{{{T_{mn}} + {\eta _{mn}}}}{{2s_{mn}^2}}} \!\right)\!{I_0}\!\left( \!{\frac{{\sqrt {{T_{mn}}{\eta _{mn}}} }}{{s_{mn}^2}}} \right)\end{array}$

(16)

其中

$s_{mn}^2 = \frac{{{\alpha ^2}E/M}}{{2\sigma _n^2}}, \quad {\eta _{mn}} = 4s_{mn}^4$

(17)

T _mn 为非中心的卡方分布， T _mn 的特征函数可表示为 ^[16] ：

$\begin{aligned}{{{Φ}}_{mn}}\left( {{\rm j}\omega } \right) = & \exp \left( { - \frac{{ {\eta _{mn}}}}{{2s_{mn}^2}}} \right)\frac{1}{{1 - 2{\rm j}\omega s_{mn}^2}}\\& \cdot \exp \left( {\frac{{{\eta _{mn}}/2s_{mn}^2}}{{1 - 2{\rm j}\omega s_{mn}^2}}} \right)\end{aligned}$

(18)

因此， ${T_1} = \sum\nolimits_{m = 1}^M {\sum\nolimits_{n = 1}^N {{T_{mn}}} } $ 的特征函数为：

${{Φ}} \left( {{\rm j}\omega } \right) = \prod\limits_{m = 1}^M {\prod\limits_{n = 1}^N {{{{Φ}} _{mn}}\left( {{\rm j}\omega } \right)} } $

(19)

为了简化分析，假设所有接收站的方差相等，即 $\sigma _1^2 = \sigma _2^2 = \cdots = \sigma _N^2 = {\sigma ^2}$ ，于是可以简化符号，使得 $s_{mn}^2 = {s^2}$ 和 ${\eta _{mn}} = \eta $ ，于是，式(19)可以写为：

${{Φ}} \left( {{\rm j}\omega } \right) = \exp \left( { - \frac{{ MN\eta }}{{2s_{}^2}}} \right)\frac{1}{{{{\left( {1 - 2{\rm j}\omega s_{}^2} \right)}^{MN}}}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\cdot \exp \left( {\frac{{MN\eta /2s_{}^2}}{{1 - 2{\rm j}\omega s_{}^2}}} \right)$

(20)

因此，可以得到 T ₁的概率密度函数为 ^[14] ：

$p\left( {{T_1}} \right) = \frac{1}{{2{s^2}}}{\left( {\frac{{{T_1}}}{{MN\eta }}} \right)^{\textstyle\frac{{MN - 1}}{2}}}\\\;\;\;\;\;\;\;\;\;\;\;\;\; \cdot \exp \left( { - \frac{{{T_1} + MN\eta }}{{2{s^2}}}} \right){I_{MN - 1}}\left( {\frac{{\sqrt {MN\eta {T_1}} }}{{{s^2}}}} \right)$

(21)

此函数被认为是自由度为2 MN 的非中心卡方分布的密度函数。

在 H ₀假设下， y _mn 仅有噪声，则有

${\left| {{y_{mn}}} \right|^2} = \frac{{{\sigma ^2}}}{2}{\left| {\frac{{{y_{mn}}}}{{\sigma /\sqrt 2 }}} \right|^2} \sim \frac{{{\sigma ^2}}}{2}\chi _{\left( 2 \right)}^2$

(22)

式中， $\chi _{\left( 2 \right)}^2$ 是自由度为2的中心卡方分布。由于

${T_0} = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {\frac{\alpha }{{\sigma _{}^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|} \right)}^2}} } \\\;\;\;\;\,= \frac{{{\alpha ^2}}}{{\sigma _{}^4}}\frac{E}{M}\frac{{{\sigma ^2}}}{2}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {\frac{{{y_{mn}}}}{{\sigma /\sqrt 2 }}} \right|}^2}} } \\\;\;\;\;\,= \frac{{{\alpha ^2}}}{{2\sigma _{}^2}}\frac{E}{M}\sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left| {\frac{{{y_{mn}}}}{{\sigma /\sqrt 2 }}} \right|}^2}} } $

(23)

则 T ₀服从自由度为2 MN 的中心卡方分布，自由度为 $\nu $ 的中心卡方分布定义为 ^[14] ：

$p\left( x \right) = \left\{ \begin{array}{l}\!\!\frac{1}{{{2^{\nu /2}}\Gamma \left( {\nu /2} \right)}}{x^{\nu /2 - 1}}\exp \left( { - \frac{x}{2}} \right), \\\;\;\;\;\;\;\;\;x > 0\\\!\!0,\;\;\;\;\;\;x < 0\end{array} \right.$

(24)

因此， T ₀的密度函数为：

$p\left(\! {{T_0}} \right) \!=\! \frac{1}{{{s^{2MN}}{2^{MN}}\Gamma \left( {MN} \right)}}T_0^{MN - 1}\exp \!\left( \!{ -\! \frac{{{T_0}}}{{2{s^2}}}} \!\right)$

(25)

其中， $\Gamma ( \cdot )$ 是伽马函数，它定义为：

$\Gamma \left( x \right) = \int_0^\infty {{t^{x - 1}}} \exp ( - t){\rm d}t$

(26)

当 x 为整数时， $\Gamma \left( x \right) = \left( {x - 1} \right)!$ 。

假设所有常量项均归入门限内，由纽曼-皮尔逊准则 ^[16] ，检测概率为：

${P_{\rm{d}}} = {Q_{MN}}\left( {\frac{{\sqrt {MN\eta } }}{s}, \frac{{\sqrt {\gamma '} }}{s}} \right) \\\;\;\;\;\;= {Q_{MN}}\left( {2s\sqrt {MN} ,\frac{{\sqrt {\gamma '} }}{s}} \right)$

(27)

其中， $\gamma '$ 为门限， $Q\left( \cdot \right)$ 为广义 Q 函数。

同样，也可以得到虚警概率为：

${P_\rm{f}} = \exp \left( { - \frac{{\gamma '}}{{2{s^2}}}} \right){\sum\limits_{k = 0}^{MN - 1} {\frac{1}{{k!}}\left( {\frac{{\gamma '}}{{2{s^2}}}} \right)} ^k}$

(28)

或

$\gamma ' = {s^2}F_{\chi _{2MN}^2}^{ - 1}\left( {1 - {P_\rm{f}}} \right)$

(29)

式中， $F_{\chi _{2MN}^2}^{ - 1}$ 表示 $\chi _{\left( {2MN} \right)}^2$ 分布的累积函数的逆函数。

4 幅相随机MIMO雷达检测器

本节将详细推导幅相随机MIMO雷达检测器结构，并重点分析低信噪比条件下平方律检测器的检测性能。

4.1 检测器结构

本节重点讨论莱斯幅度模型的最优检测器。为了清晰地表示未知幅度的依赖性，将式(5)重新写为如下形式：

$\begin{array}{l}{p_1}\!\left( {{y}|{{β}},\!{{α}}}\! \right) = \\\prod\limits_{m = 1}^M\! {\prod\limits_{n = 1}^N\!\! {\frac{1}{{{{π}} \sigma _n^2}}} } \!\exp\!\! \left(\!\!\! { -\! \frac{1}{{\sigma _n^2}}\!\!{{\left| {{y_{mn}} \!-\!\! \sqrt {\frac{E}{M}} {\alpha \!_{mn}}{{\rm e}^{{\rm j}{\beta _{mn}}}}}\! \right|}^2}}\! \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \prod\limits_{m = 1}^M {\prod\limits_{n = 1}^N {\frac{1}{{{{π}} \sigma _n^2}}} } \exp \left( { - \frac{1}{{\sigma _n^2}}{{\left| {{y_{mn}}} \right|}^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot \exp \left( { - \frac{E}{{M\sigma _n^2}}\alpha _{mn}^2} \right) \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot \exp\! \left(\! {\frac{{2{\alpha _{mn}}}}{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|\cos \left( {{\beta _{mn}} - {\zeta _{mn}}} \right)} \!\right)\end{array}$

(30)

式中， ${{α}} = [{\alpha _{11}} \ \:{\alpha _{21}}\: \cdots \:\:{\alpha _{MN}}]$ 。首先，在 MN 个相互独立的未知相位上求平均，得到仅关于发射系数 ${{α}}$ 的条件分布，

${p_1}\left( {{y}|{{α}}} \right) = \prod\limits_{m = 1}^M {\prod\limits_{n = 1}^N {\frac{1}{{{{π}} \sigma _n^2}}} } \exp \left( { - \frac{1}{{\sigma _n^2}}{{\left| {{y_{mn}}} \right|}^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot \exp \!\left( \!{ -\! \frac{E}{{M\sigma _n^2}}\!\alpha _{mn}^2} \!\right) {I_0}\left(\! {\frac{{2{\alpha _{mn}}}}{{\sigma _n^2}}\!\sqrt {\frac{E}{M}}\! \left| {{y_{mn}}} \right|} \!\right)$

(31)

假设，各个路径上的反射系数的幅度均服从莱斯分布，且有

$p\left( {{\alpha _{mn}}} \right) = \frac{{{\alpha _{mn}}}}{{\tilde \sigma _{mn}^2}}\exp \left( { - \frac{1}{{2\tilde \sigma _{mn}^2}}\left( {\alpha _{mn}^2 + \chi _{mn}^2} \right)} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdot{I_0}\left( {\frac{{{\alpha _{mn}}{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}} \right)$

(32)

式中， $\chi _{mn}^2$ 与能量呈正比，并且 $\tilde \sigma _{mn}^2$ 与多径能量呈正比。如果 $\chi _{mn}^2 = 0$ ，则密度函数为瑞利分布。利用式(32)，非条件密度函数可以表示为：

$\begin{array}{l}{p_1}\!\left( {y} \right) \!\!=\!\! \int\! {{p_1}\left( {{y}|{{α}}} \right)p\left( {{α}} \right)} {\rm d}{{α}}\\\;\;\;\;\;\;\;\; =\! \prod\limits_{m = 1}^M\! {\prod\limits_{n = 1}^N \!{\frac{1}{{{{π}} \sigma _n^2}}} }\! \exp \! \left(\! { \!-\! \frac{1}{{\sigma _n^2}}\!{{\left| {{y_{mn}}} \right|}^2} \!-\! \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}}}\!\! \right) \\\;\;\;\;\;\;\;\;\;\;\cdot \int_0^\infty \! \!\!\!{\frac{{{\alpha _{mn}}}}{{\tilde \sigma _{mn}^2}}} \exp \left( { - \alpha _{mn}^2\left[ {\frac{E}{{M\sigma _n^2}} + \frac{1}{{2\tilde \sigma _{mn}^2}}} \right]} \right) \\\;\;\;\;\;\;\;\;\;\;\cdot {I_0}\!\left( \!{\frac{{2{\alpha _{mn}}}}{{\sigma _n^2}}\!\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|}\!\!\right)\!\!{I_0}\!\left(\!\! {\frac{{{\alpha _{mn}}{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}}\!\! \right)\!\!{\rm d}{\alpha _{mn}}\end{array}$

(33)

式(33)由如下公式计算 ^[15] ：

$\int_0^\infty \!\!\!\! {\alpha \exp \left( { - c{\alpha ^2}} \right){I_0}\left( {g\alpha } \right){I_0}\left( {e\alpha } \right)} {\rm d}\alpha \\\;\;\;\;\;\;\;\;\;\;\;= \frac{1}{{2c}}\exp \left( {\frac{{{g^2} + {e^2}}}{{4c}}} \right){I_0}\left( {\frac{{ge}}{{2c}}} \right)$

(34)

因此， H ₁下的联合密度函数为：

${p_1}\!\left( \!{y} \!\right) \!\!=\!\! \prod\limits_{m = 1}^M\! {\prod\limits_{n = 1}^N\! {\frac{1}{{{{π}} \sigma _n^2\tilde \sigma _{mn}^2}}} } \exp \!\left(\! { - \!\frac{1}{{\sigma _n^2}}\!\!{{\left| {{y_{mn}}} \right|}^2} \!\!- \!\!\frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}}}\! \right) \\\;\;\;\;\;\;\;\;\;\cdot \frac{1}{{2{c_{mn}}}}{\rm exp} \left( {\frac{{g_{mn}^2 + e_{mn}^2}}{{4{c_{mn}}}}} \right){I_0}\left( {\frac{{{g_{mn}}{e_{mn}}}}{{2{c_{mn}}}}} \right)$

(35)

式中

${c_{mn}} = \frac{E}{{M\sigma _n^2}} + \frac{1}{{2\tilde \sigma _{mn}^2}}$

(36)

随机变量 g _mn 为：

${g_{mn}} = \frac{2}{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|$

(37)

且

${e_{mn}} = \frac{{{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}$

(38)

由式(35)和式(8)，可得似然比为：

$\ln L\left( {y} \right) = \ln \left( {\frac{{{p_1}\left( {y} \right)}}{{{p_0}\left( {y} \right)}}} \right) = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{W_{mn}}} } $

(39)

这里，

${W_{mn}} = - 2\ln \left( {{{\tilde \sigma }_{mn}}} \right) - \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}} - \ln \left( {2{c_{mn}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;+ \frac{{g_{mn}^2 + e_{mn}^2}}{{4{c_{mn}}}} + \ln {I_0}\left( {\frac{{{g_{mn}}{e_{mn}}}}{{2{c_{mn}}}}} \right)$

(40)

本节对 $\ln {I_0}( \cdot)$ 采用低信噪比时的平方律近似，由式(40)，可以得到

${W_{mn}} = g_{mn}^2\left( {\frac{1}{{4{c_{mn}}}} + \frac{{e_{mn}^2}}{{4c_{mn}^2}}} \right) - 2\ln \left( {{{\tilde \sigma }_{mn}}} \right) \\ \;\;\;\;\;\;\;\;\;\;\;\;- \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}} - \ln \left( {2{c_{mn}}} \right) + \frac{{e_{mn}^2}}{{4{c_{mn}}}}$

(41)

因为 ${g_{mn}} = \displaystyle\frac{2}{{\sigma _n^2}}\sqrt {\frac{E}{M}} \left| {{y_{mn}}} \right|$ ，所以有

$\begin{array}{l}{W_{mn}} = \frac{4}{{\sigma _n^4}}\frac{E}{M}{\left| {{y_{mn}}} \right|^2}\left( {\frac{1}{{4{c_{mn}}}} + \frac{{e_{mn}^2}}{{4c_{mn}^2}}} \right) - 2\ln \left( {{{\tilde \sigma }_{mn}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;- \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}} - \ln \left( {2{c_{mn}}} \right) + \frac{{e_{mn}^2}}{{4{c_{mn}}}}\\\;\;\;\;\;\;\;\;\; = {\left( {{a_{mn}}\left| {{y_{mn}}} \right|} \right)^2} \!-\! 2\ln \left( {{{\tilde \sigma }_{mn}}} \right)\! -\! \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}}\\ \;\;\;\;\;\;\;\;\;\;\;\;-\ln \left( {2{c_{mn}}} \right) \!+\! \frac{{e_{mn}^2}}{{4{c_{mn}}}}\end{array}$

(42)

其中

${a_{mn}} = \sqrt {\frac{4}{{\sigma _n^4}}\frac{E}{M}\left( {\frac{1}{{4{c_{mn}}}} + \frac{{e_{mn}^2}}{{4c_{mn}^2}}} \right)} \\\;\;\;\;\;\;\,{\rm{ = }}\sqrt {\displaystyle\frac{{\displaystyle\frac{{E/M}}{{\sigma _n^4}}\left( {\left( {\displaystyle\frac{{E/M}}{{\sigma _n^2}} + \displaystyle\frac{1}{{2\tilde \sigma _{mn}^2}}} \right) + \displaystyle\frac{{\chi _{mn}^2}}{{\tilde \sigma _{mn}^4}}} \right)}}{{{{\left( {\displaystyle\frac{{E/M}}{{\sigma _n^2}} + \frac{1}{{2\tilde \sigma _{mn}^2}}} \right)}^2}}}} $

(43)

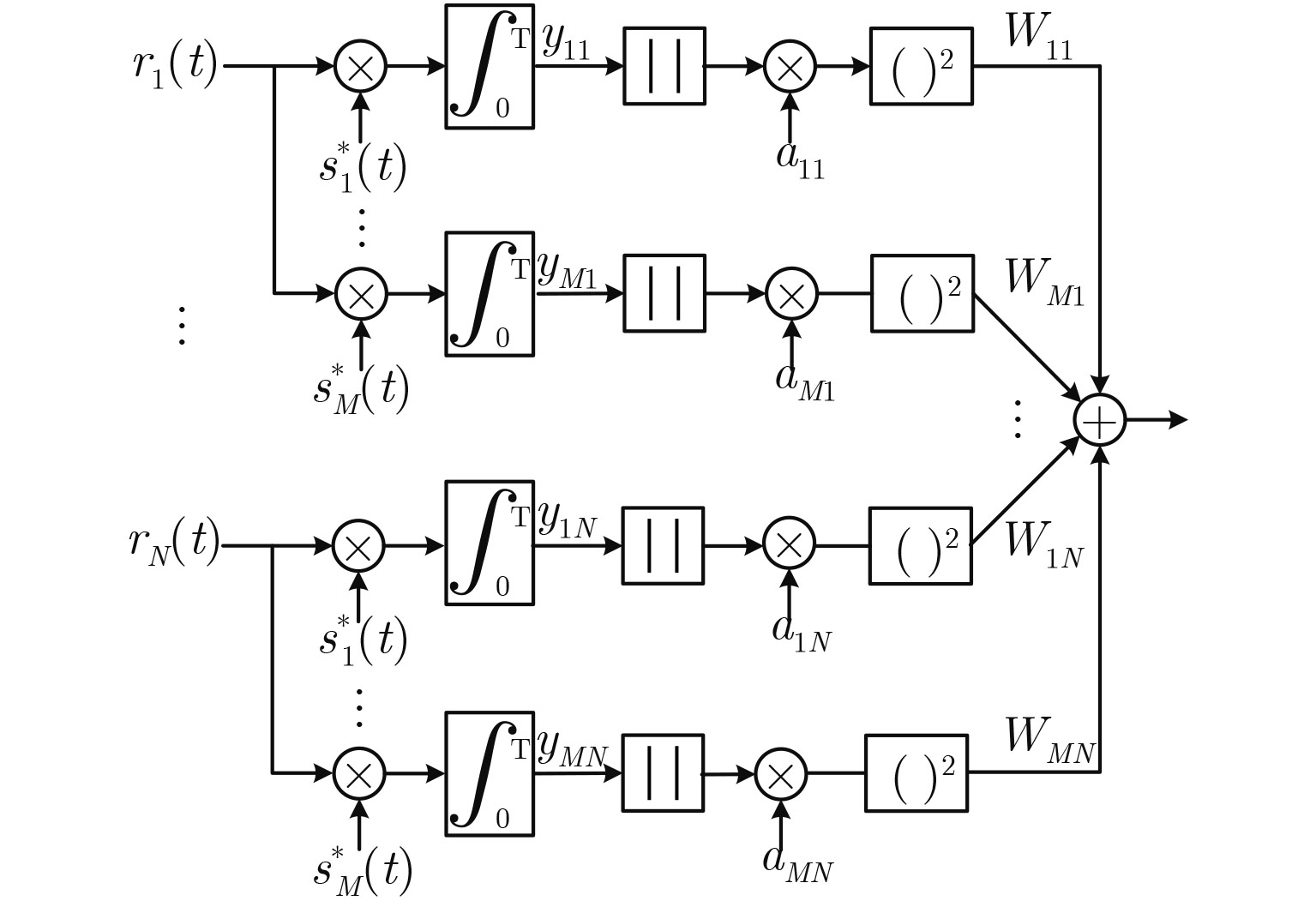
假设所有的常量归入门限内，其平方律合并检测器可简化为 图3 ，图中给出检测统计量式(39)的检测器结构。

4.2 检测器性能分析

类似于3.2小节中非相参MIMO雷达检测性能分析。将式(12)重新表示为条件密度函数：

$p\left( {\left| {{y_{mn}}} \right||{\alpha _{mn}}} \right) = \frac{{\left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}\exp \left( { - \frac{{{{\left| {{y_{mn}}} \right|}^2} + E\alpha _{mn}^2/M}}{{2\sigma _n^2/2}}} \right)\\\;\;\;\;\;\; \quad \quad \quad \quad \quad \cdot {I_0}\left( {\frac{{\sqrt {\displaystyle\frac{E}{M}} {\alpha _{mn}}\left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}} \right) \ $

(44)

因此，由式(32)， ${\alpha _{mn}}$ 服从莱斯分布，无条件密度函数为：

$\begin{array}{l}p\left( {\left| {{y_{mn}}} \right|} \right) = \int_0^\infty {p\left( {\left| {{y_{mn}}} \right||{\alpha _{mn}}} \right)p\left( {{\alpha _{mn}}} \right)} {\rm d}{\alpha _{mn}}\\ \quad \quad \quad \ \ \,= \int_0^\infty {\left\{ {\frac{{\left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}\exp \left( { - \frac{{{{\left| {{y_{mn}}} \right|}^2} + E\alpha _{mn}^2/M}}{{2\sigma _n^2/2}}} \right){I_0}\left( {\frac{{\sqrt {\displaystyle\frac{E}{M}} {\alpha _{mn}}\left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}} \right)} \right\}} \\ \quad \quad \quad \quad \quad \cdot \left\{ {\frac{{{\alpha _{mn}}}}{{\tilde \sigma _{mn}^2}}\exp \left( { - \frac{1}{{2\tilde \sigma _{mn}^2}}\left( {\alpha _{mn}^2 + \chi _{mn}^2} \right)} \right){I_0}\left( {\frac{{{\alpha _{mn}}{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}} \right)} \right\}{\rm d}{\alpha _{mn}}\\ \quad \quad \quad \ \ \,= \frac{{\left| {{y_{mn}}} \right|}}{{\tilde \sigma _{mn}^2\sigma _n^2/2}}\exp \left( { - \frac{{{{\left| {{y_{mn}}} \right|}^2}}}{{2\sigma _n^2/2}} - \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}}} \right) \\ \quad \quad \quad \quad \quad \cdot \int_0^\infty {{\alpha _{mn}}\exp \left( { - \alpha _{mn}^2\left( {\frac{{E/M}}{{2\sigma _n^2/2}} + \frac{1}{{2\tilde \sigma _{mn}^2}}} \right)} \right)} {I_0}\left( {\frac{{\sqrt {\displaystyle\frac{E}{M}} {\alpha _{mn}}\left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}} \right){I_0}\left( {\frac{{{\alpha _{mn}}{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}} \right){\rm d}{\alpha _{mn}}\\\end{array}$

(45)

又根据 ^[14]

$\int_0^\infty \alpha \exp \left( { - p{\alpha ^2}} \right){I_0}\left( {a\alpha } \right){I_0}\left( {\beta \alpha } \right){\rm d}\alpha \\ \quad \quad \ \ \ = \frac{1}{{2p}}\exp \left( {\frac{{{a^2} + {\beta ^2}}}{{4p}}} \right){I_0}\left( {\frac{{a\beta }}{{2p}}} \right)$

(46)

可求解式(46)，得

$\begin{array}{*{20}{l}}\begin{array}{l}p\left( {\left| {{y_{mn}}} \right|} \right) = \frac{{\left| {{y_{mn}}} \right|}}{{\tilde \sigma _{mn}^2\sigma _n^2/2}}\exp \left( { - \frac{{{{\left| {{y_{mn}}} \right|}^2}}}{{2\sigma _n^2/2}} - \frac{{\chi _{mn}^2}}{{2\tilde \sigma _{mn}^2}}} \right)\\ \quad \quad \quad \quad \quad \cdot \frac{1}{{2\left( {\displaystyle\frac{{E/M}}{{2\sigma _n^2/2}} + \displaystyle\frac{1}{{2\tilde \sigma _{mn}^2}}} \right)}}\end{array}\\ \begin{array}{l} \quad \quad \quad \quad \quad \cdot \exp \left( {\frac{{{{\left( {\displaystyle\frac{{\sqrt {\displaystyle\frac{E}{M}} \left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}} \right)}^2} + {{\left( {\displaystyle\frac{{{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}} \right)}^2}}}{{4\left( {\displaystyle\frac{{E/M}}{{2\sigma _n^2/2}} + \displaystyle\frac{1}{{2\tilde \sigma _{mn}^2}}} \right)}}} \right)\\ \quad \quad \quad \quad \quad \cdot {I_0}\left( {\displaystyle\frac{{\left( {\displaystyle\frac{{\sqrt {\displaystyle\frac{E}{M}} \left| {{y_{mn}}} \right|}}{{\sigma _n^2/2}}} \right)\left( {\displaystyle\frac{{{\chi _{mn}}}}{{\tilde \sigma _{mn}^2}}} \right)}}{{2\left( {\displaystyle\frac{{E/M}}{{2\sigma _n^2/2}} + \displaystyle\frac{1}{{2\tilde \sigma _{mn}^2}}} \right)}}} \right)\end{array}\\ \begin{array}{l} \quad \quad \quad \quad \!= \frac{{\left| {{y_{mn}}} \right|}}{{\tilde \sigma _{mn}^2E/M + \sigma _n^2/2}}\\ \quad \quad \quad \quad \quad \cdot \exp \left( { - \frac{{{{\left| {{y_{mn}}} \right|}^2} + \chi _{mn}^2E/M}}{{2\tilde \sigma _{mn}^2E/M + \sigma _n^2}}} \right)\\ \quad \quad \quad \quad \quad \cdot {I_0}\left( {\frac{{\left| {{y_{mn}}} \right|{\chi _{mn}}\sqrt {E/M} }}{{\tilde \sigma _{mn}^2E/M + \sigma _n^2/2}}} \right)\end{array}\end{array}$

(47)

此式可以看作另一个莱斯分布，剩下的过程跟相位未知的情况类似。

假设 ${T_{mn}} = {\left( {{a_{mn}}\left| {{y_{mn}}} \right|} \right)^2}$ ，由此可得到 T _mn 的概率密度函数为：

$\begin{array}{l}p\left( {{T_{mn}}} \right) = \frac{1}{{2a_{mn}^2\left( {\tilde \sigma _{mn}^2E/M + \sigma _n^2/2} \right)}}\\ \quad \quad \quad \quad \; \cdot \exp \left( { - \frac{{{T_{mn}} + a_{mn}^2\chi _{mn}^2E/M}}{{2a_{mn}^2\left( {\tilde \sigma _{mn}^2E/M + \sigma _n^2/2} \right)}}} \right)\\ \quad \quad \quad \quad \; \cdot {I_0}\left( {\frac{{\sqrt {{T_{mn}}} {\chi _{mn}}\sqrt {E/M} }}{{{a_{mn}}\left( {\tilde \sigma _{mn}^2E/M + \sigma _n^2/2} \right)}}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\; =\! \frac{1}{{2s_{mn}^2}}\exp\! \left(\! { -\! \frac{{{T_{mn}} \!+\! {\eta _{mn}}}}{{2s_{mn}^2}}} \right)\!{I_0}\!\left(\! {\frac{{\sqrt {{T_{mn}}{\eta _{mn}}} }}{{s_{mn}^2}}}\! \right)\end{array}$

(48)

其中

$\left. {\begin{array}{*{20}{c}}{s_{mn}^2 = a_{mn}^2\left( {\tilde \sigma _{mn}^2E/M + \sigma _n^2/2} \right)}\\{{\eta _{mn}} = a_{mn}^2\chi _{mn}^2E/M} \quad \quad \quad \quad \end{array}} \right\}$

(49)

只有假设所有接收站的噪声方差相等，即 $\sigma _1^2 =$ $\sigma _2^2 = \cdots = \sigma _N^2 = {\sigma ^2}$ ，才能进一步分析，则可利用相位未知所采用的方法。

5 仿真实验

本节分别仿真了相位随机MIMO雷达和幅相随机MIMO雷达检测器的检测概率曲线。仿真对比了不同收发站数目对MIMO雷达仿真性能的影响。

5.1 相位随机MIMO雷达检测性能

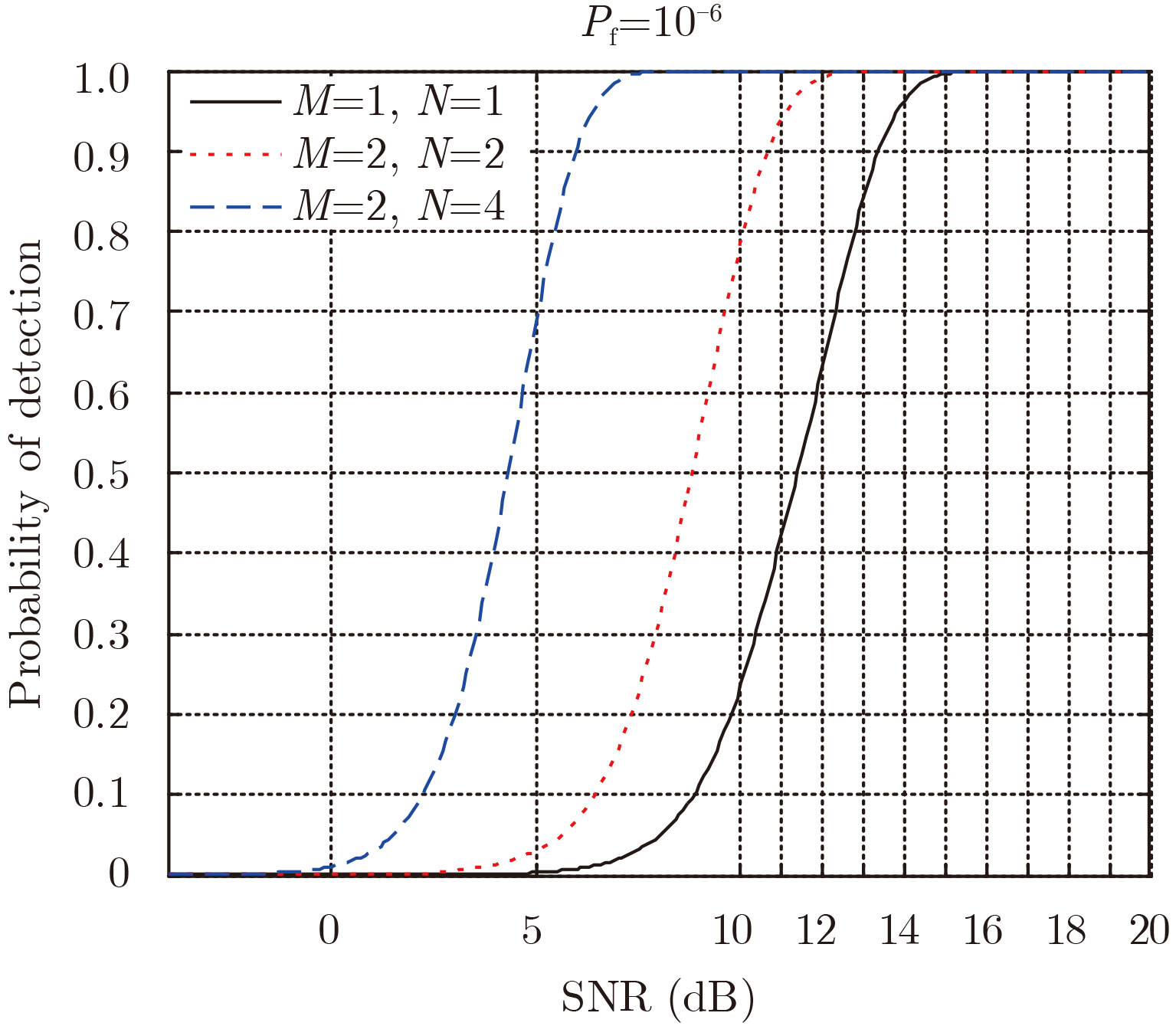
图4 对比了不同数目的收发站，相位随机MIMO雷达检测性能曲线。仿真中，固定虚警概率 P _f=10 ^–6 。每个路径相位服从 $(0,2{{π}} )$ 之间的均匀分布。

从 图4 可以看出，随着观测路径的增加，要想达到同单路径相同的检测性能需要更低的信噪比。在 图4 中，要达到0.8的检测概率，单发单收雷达系统需要将近12.8 dB信噪比，2发2收的系统需要10.1 dB信噪比，而2发4收的系统仅需要5.5 dB信噪比。相比于单发单收系统，改善增益分别为2.7 dB和7.3 dB，这就是分集增益带来的信噪比的改善，而且改善的增益介于 $10\log (\sqrt {MN} )$ 和 $10\log (MN)$ 之间。这对工程应用具有重要的指导意义，特别是对反隐身，针对单部雷达反隐身能力不足，可以通过多部雷达组成分布式MIMO雷达系统，利用分布式MIMO雷达系统的分集增益，以达到反隐身的目的。

5.2 幅相随机MIMO雷达检测性能

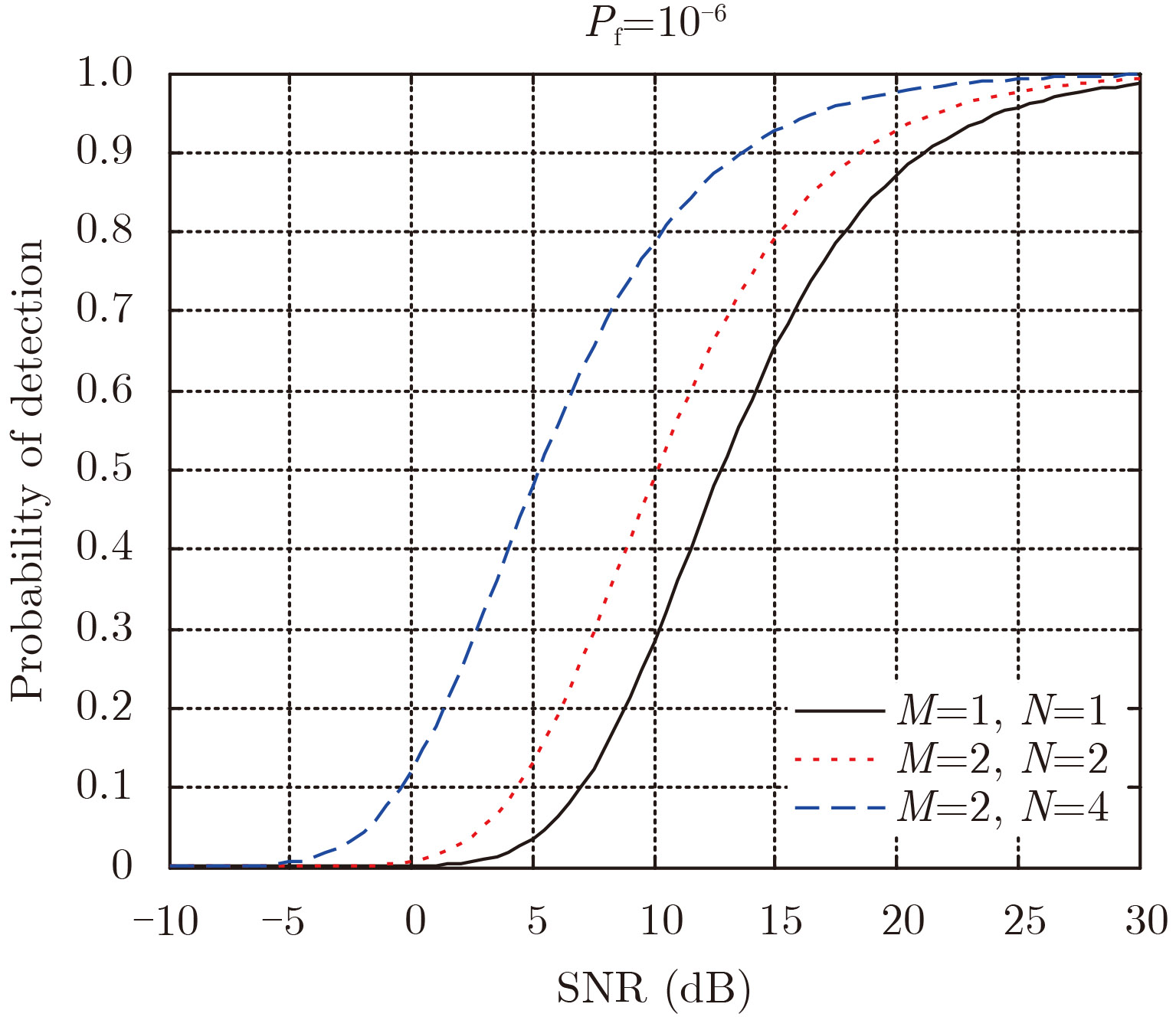
图5 对比了在虚警概率为 P _f=10 ^–6 时，不同数目的收发站，幅相随机MIMO雷达检测性能曲线。每个路径的幅度服从均值为0，方差为1的莱斯分布，相位服从 $(0,2{{π}} )$ 之间的均匀分布。

从 图5 中可以看出，在幅相随机的场景下，要达到0.8的检测概率，单发单收雷达系统需要将近18 dB信噪比，2发2收的系统需要15 dB信噪比，而2发4收的系统仅需要10.5 dB信噪比。相比于单发单收系统，改善增益分别为3.0 dB和7.5 dB，这种改善增益也介于 $10\log (\sqrt {MN} )$ 和 $10\log (MN)$ 之间。同时，对比 图4 和 图5 ，在相同的条件下，幅相随机比仅相位随机，需要更大的信噪比，这与工程实际也是相符的，因为多了个随机变量，目标的检测性能应该下降。

6 小结

本文根据分布式MIMO雷达站相对于目标的分布场景，分别说明了分布式MIMO雷达3种工作形态，即，分布式相参MIMO雷达、相位随机MIMO雷达和幅相随机MIMO雷达，后两者亦是非相参MIMO雷达。随后，本文推导了非相参MIMO雷达检测器，相位服从 $(0,2{{π}} )$ 均匀分布，幅度服从莱斯分布模型，并详细分析了两种情况的非相参MIMO雷达检测的检测性能。最后，本文通过仿真说明了非相参MIMO雷达的分集增益带来的信噪比的改善，这种改善的增益介于 $10\log (\sqrt {MN} )$ 和 $10\log (MN)$ 之间。本文的结论对工程应用具有重要的指导意义。