1 引言

高分辨率合成孔径雷达(Synthetic Aperture Radar, SAR)可以获得丰富的地物或目标细节，在军事和民用各方面有着非常高的应用价值。然而高分辨率带来了更长的合成孔径时间，这使得目标运动对成像的影响更加显著。尤其在海面或港口，受到海面风浪的影响，舰船等目标将存在复杂的运动，使得舰船自身的散射以及舰船与海面的多次散射均存在合成孔径时间内的变化特性，导致SAR图像存在严重的散焦现象，给目标检测、识别和图像解译带来困难。因此高分辨率SAR中运动目标的精细聚焦是当前SAR应用迫切需要解决的问题之一。

国内外有关SAR运动目标的研究着重于地面运动目标指示(GMTI)^[1,2]、运动目标成像算法、运动目标多普勒参数估计等方面^[3,4]，研究大部分基于原始回波开展，以匀速直线运动、匀变速直线运动为主^[5,6]。其中关于海面舰船的研究也主要是以平动为主、基于机载SAR模型开展运动误差的分析^[7]。涉及舰船复杂运动的大多数研究则侧重于依靠舰船自身运动(如俯仰、横滚、偏航等3维运动)使用逆合成孔径雷达(ISAR)成像原理实现舰船目标的高分辨率成像^[8,9]。目前非常缺少从高分辨率星载SAR图像产品出发，对散焦的海面复杂运动目标进行精细化分析处理的研究，也缺少对复杂运动信息进行估计与提取的研究。

鉴于此，本文主要针对高分辨率星载SAR中目标起伏运动引入的误差进行了定量化分析，并仿真了其在SAR图像中的成像特点，提出了一种基于复图像数据进行运动误差补偿和精细聚焦处理的方法，估计得到目标的运动参数和海浪信息，仿真和实际数据的处理结果验证了本文分析的正确性和方法的有效性。本文结构安排如下：第2节建立星载SAR目标起伏运动下的几何模型，定量化分析起伏运动与海面二次散射引入的误差与影响；第3节提出精细聚焦处理方法和运动参数估计方法；第4节给出了仿真实验和TerraSAR-X港口区域实际数据实验处理结果；第5节总结全文。

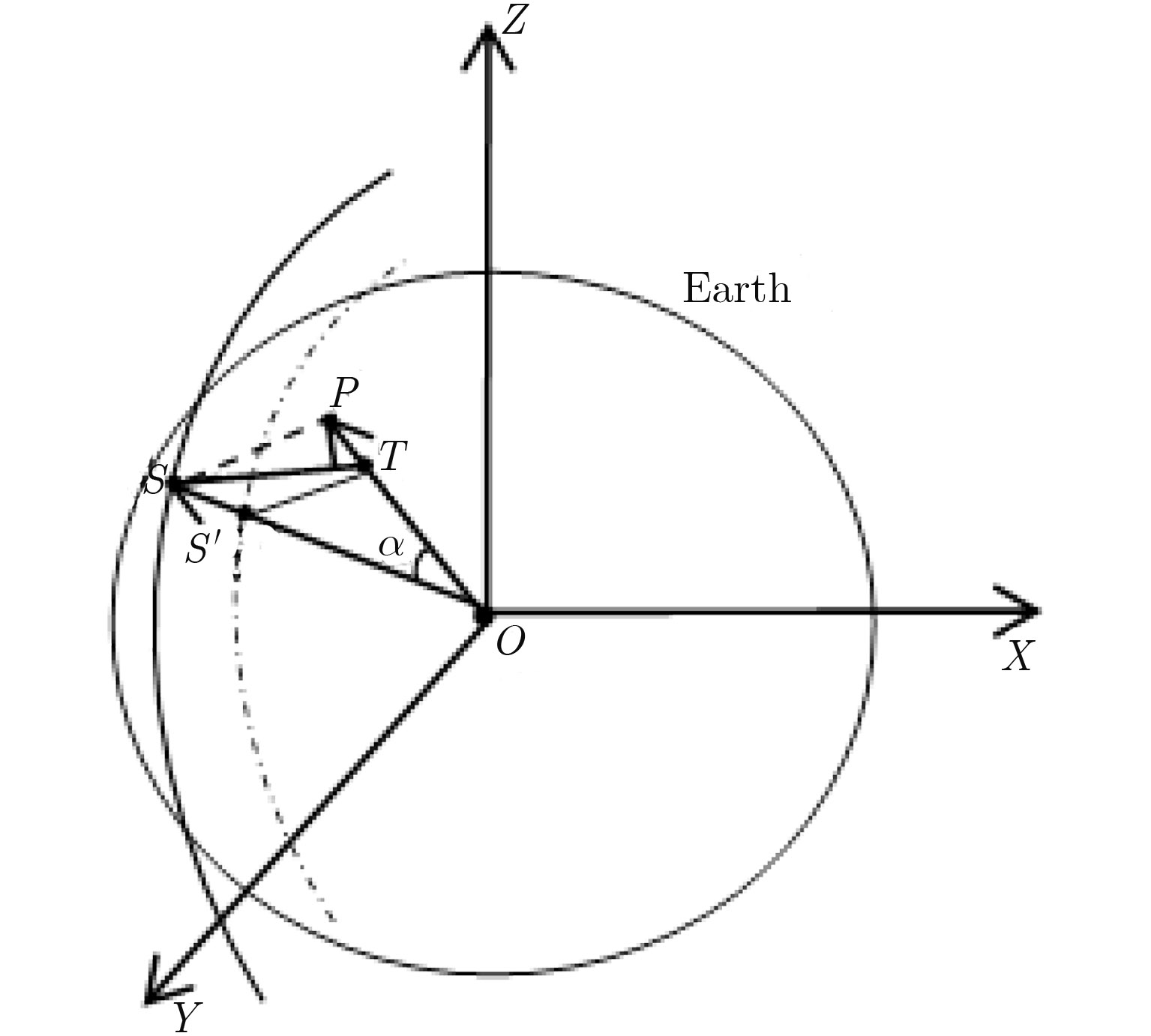
2 星载SAR起伏运动目标信号模型与误差 分析 2.1 起伏运动目标单次散射误差分析

图1为星载起伏运动点目标成像几何。T和P分别为某一方位时刻h目标静止和起伏运动的位置，S为该时刻的卫星位置，设起伏运动沿地球矢径方向，幅度为A，频率为$\omega $，初相为 $\varphi $ ，点P相对于点T的距离矢量为：

$ \rm{TP}= {A} \cdot \sin (\omega \eta + \varphi )$

(1)

其中 A 为目标沿 TP方向振动的幅度矢量。

点P的距离历程为：

$\begin{split}{R_{{\rm v}}}(\eta ) &\!\!\!\!\! = \left| {{{ \rm{PS}}}} \right| = \left| {{{\rm{ TS}}} - {\rm{TP}}} \right|\\ &\!\!\!\!\! = \!\sqrt {{{\left| {{\rm{TS}}} \right|}^2}\! +\! {{\left| {{\rm{TP}}} \right|}^2} \!-\! 2\left| {{\rm{TS}}} \right|\left| {{\rm{TP}}} \right| \cos\gamma } \end{split}$

(2)

其中$\gamma $为目标点T处的波束入射角，计算公式为：

$\gamma = \alpha + \beta $

(3)

其中$\beta $为卫星下视角，$\alpha $为卫星与目标之间的地心角。

将式(2)作近似处理：

$\begin{aligned}{R_{\rm v}}(\eta ) & = \sqrt {{{\left| {{\rm{TS}}} \right|}^2} \!\!+\!\! {{\left| {{\rm{TP}} \! \cdot\! {{\cos \gamma }}} \right|}^2}\!\! -\!\! 2 \!\cdot\! \left| {{\rm{TS}}} \right|\! \cdot\! \left| {{\rm{TP}}} \right| \!\cdot\! \cos\gamma } \\&= \left| {{\rm{TS}}} \right| - \left| {{\rm{TP}}} \right| \cdot \cos\gamma \end{aligned} $

(4)

计算得到目标起伏运动引入的距离历程误差为：

$\Delta R(\eta ) = A \cdot \cos \gamma \cdot \sin (\omega \eta + \varphi )$

(5)

根据SAR回波与成像理论，进一步计算得到相位误差为：

$\Delta \varphi (\eta ) = \exp \left\{ { - {\rm j}\frac{{4{π} }}{\lambda } \cdot A \cdot \cos \gamma \cdot \sin (\omega \eta + \varphi )} \right\}$

(6)

对式(6)做Jacobi-Angle展开，得到：

$\left. \begin{array}{l} \Delta \varphi (\eta ) = {J_0}(b) + \sum\limits_{n = 1}^\infty {{J_n}(b)} \\ \;\;\;\;\;\;\;\; \cdot \left[ {{{\rm{e}}^{{\rm{j}}n\varphi }}{{\rm{e}}^{{\rm{j}}n\omega \eta }} + {{( - 1)}^n}{{\rm{e}}^{ - {\rm{j}}n\varphi }}{{\rm{e}}^{ - {\rm{j}}n\omega \eta }}} \right]\\ b = \frac{{4\pi }}{\lambda } \cdot A \cdot \cos \gamma \end{array} \right\}$

(7)

其中 $J_0( \cdot )$ 是第一类n阶贝塞尔函数。

可见式(7)中的指数项将导致多重对称的多普勒频移，产生成对回波，成像结果在方位向上将出现原信号的多重对称复制，进而引起散焦现象，其散焦程度与起伏运动的幅度和周期有关。

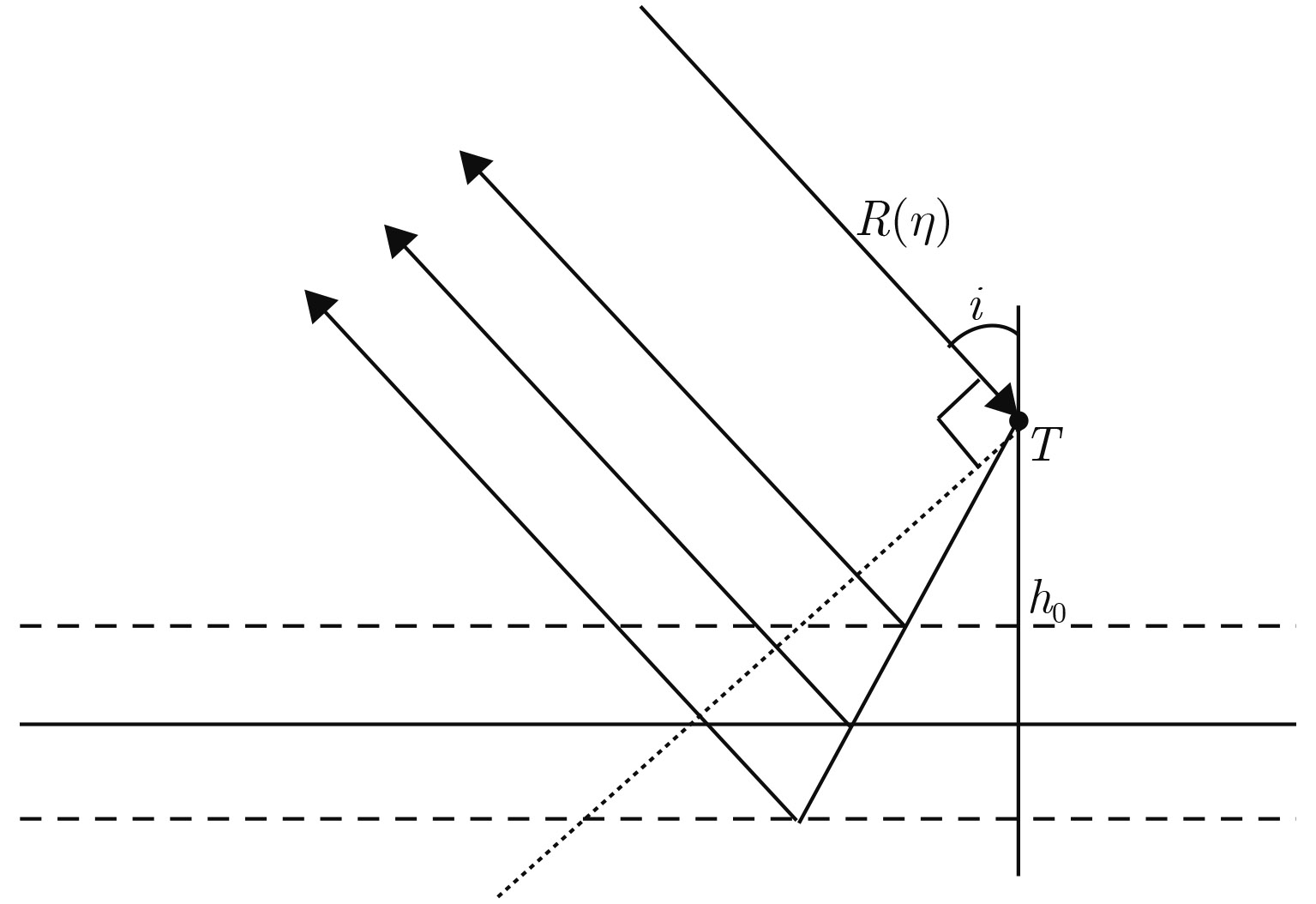
2.2 海面起伏二次散射误差分析

部分海面目标具有垂直于海面的结构，该结构会引起目标与海面间的多次散射。若海面静止，该结构与海面形成一个理想的二面角结构，但由于海风与地理结构的关系，海面存在着复杂的起伏运动，使二次散射的距离历程发生变化，进而影响成像结果。如图2所示，目标T为垂直结构上的任一散射点，某方位时刻$\eta $天线波束以入射角经过目标点T，并经由海面二次散射返回雷达接收机，图中实线为静止海面，虚线表示海面的起伏状态，设目标T距离静止海面的高度为h₀，该时刻与雷达之间的距离为R($\eta $)，海面起伏运动的幅度为A，周期为$\omega $，初相为 $\varphi $ 。目标T的往返距离历程为：

$\begin{split}R'(\eta ) = & \!\!\!\!2R(\eta ) + \frac{h}{{\cos i}} + \frac{{h\sin (2{π} - 2i)}}{{\cos i}}\\ = &\!\!\!\! 2R(\eta ) + 2h\cos i\end{split}$

(8)

其中 $h = h_0 + A\sin (\omega \eta + \varphi )$ 。

当海面静止时，目标T的往返距离历程为：

${R_0}(\eta ) = 2R(\eta ) + 2{h_0}\cos i$

(9)

计算得到海面起伏运动引入的二次散射距离历程误差为：

$\Delta R = R'(\eta ) - {R_0}(\eta ) = 2A\cos i\sin (\omega \eta + \varphi )$

(10)

式(10)与式(5)具有相同的形式，其区别主要在于幅度、频率和初相的不同，但对成像结果产生的影响具有相同的规律，在此不做赘述。实际上，本文考虑的二次散射是类似二面角的二次散射，其距离历程等效为二面角角点的单次散射，因此本文后续的精细聚焦及参数估计算法对单次散射模型和二次散射模型是通用的。需要说明的是，由于二次散射通常比单次散射具有更大的强度，运动对二次散射的影响往往在图像上表现的更为突出。

3 精细聚焦算法与参数估计 3.1 基于复图像数据的精细聚焦算法

针对含有运动目标的复图像数据，本文提出的精细聚焦算法具体实现步骤如图3所示。

(1) 方位向反压缩

通过方位匹配滤波器逆乘将数据变换至多普勒域，设多普勒频率为${f_\eta }$，距离向时间为t，后向散射系数为$\sigma $，雷达波长为$\gamma $，发射信号带宽为B，则得到方位向未压缩的数据：

$\begin{split}S(t,{f_\eta })= \!\!\! & \sigma ({f_\eta }) \cdot {\rm sinc} \left\{ {{π} B\left[ {t - \frac{{2R({f_\eta })}}{c}} \right]} \right\}\\& \cdot \exp\left[ {\frac{{ - {\rm j}4{π} R({f_\eta })}}{\lambda }} \right]\end{split}$

(11)

其中 $R(\eta ) = R + \Delta R(f_{η})$ ，R为方位零时刻目标与雷达间斜距， $\Delta R(f_{η} )$ 表示运动引起的斜距误差，其形式由具体运动的误差分析得到。

(2) 距离包络对准

对方位未压缩数据应用最小熵距离对准算法^[10]，实现目标的距离向包络对齐，在不需要提供先验知识的情况下，消除运动产生的相邻回波在距离向上的错位。这是一个最优化问题，目标函数为所有1维距离像和的熵值，可以表示为：

$\begin{split}\left.\begin{aligned}E & \left[ {{\Delta r}(1),{\Delta r}(2), ·\!·\!· ,{\Delta r}(N - 1)} \right]\\& = - \int_r {\frac{{{p_{\rm ave}}(r)}}{S}} \cdot \ln \frac{{{p_{\rm ave}}(r)}}{S}{\rm d}r\\S & = \int_r {{p_{\rm ave}}(r)} {\rm d}r\end{aligned}\right \}\end{split}$

(12)

其中 $p_{\rm ave}(r)$ 表示所有目标1维距离像的和：

${p_{\rm ave}}(r) = \sum\limits_{n = 0}^{N - 1} {p(r + {\Delta r}(n),n)} $

(13)

其中r为距离向采样点， $\Delta r(n)$ 代表第n个回波的距离偏移量。

$p_{\rm ave}(r)$ 的锐化度可以用来衡量回波包络对齐的程度，锐化度达到最高时，回波基本对齐。而香农熵可以用来衡量 $p_{\rm ave}(r)$ 的锐化程度，波形锐化度越高，熵值越小，因此最优化准则为 $p_{\rm ave}(r)$ 的熵值最小，通过迭代可以得到 $\Delta r(n)$ 全局最优解。理论上此方法的对准精度为一个距离分辨单元，为了适应高分辨率的要求，本文实验均对输入数据在距离向做了32倍插值，使实际的对准精度达到1/8～1/4个距离分辨单元。

(3) 相位误差校正

将距离对准后的数据变换至多普勒域，由于各次回波间的相位误差通常可以和雷达波长相比拟，用距离偏移量来校正相位不精确，因此本文应用自聚焦算法实现误差相位校正。相比于基于特显点的自聚焦算法(Phase Gradient Autofocus, PGA等)，基于图像整体信息的自聚焦算法在低信噪比和低图像对比度的条件下具有更好的鲁棒性，能够取得更好的聚焦效果。本文采用全局最小熵的相位校正算法(Minimum Entropy Autofocus, MEA)^[11]，该算法是一个求解补偿相位使图像聚焦效果最好的最优化问题，目标函数为一幅图像的熵值：

$\varepsilon \left[ {{{\left| {g(r,n)} \right|}^2}} \right] = - \sum\limits_{r = 0}^{M - 1} {\sum\limits_{n = 0}^{N - 1} {{{\left| {g(r,n)} \right|}^2}} } \ln {\left| {g(r,n)} \right|^2}$

(14)

其中n为方位向采样点， $g(r,n)$ 为经过相位补偿的图像，可以表示为：

$g(r,n) = \sum\limits_{m = 0}^{N - 1} {f(r,m){{\rm e}^{{\rm j}\Delta \varphi (m)}}{{\rm e}^{ - {\rm j}{\Large\frac{{2{π} }}{M}}nm}}} $

(15)

其中 $f(r,m)$ 表示距离对准后方位频域的数据， $\Delta \varphi (m)$ 表示第m个回波的相位补偿量。

图像的聚焦程度可以用图像的熵来衡量，聚焦程度越高，图像的熵就越小，图像也越清晰。因此最优化准则为式(14)的值达到最小，在给定补偿相位初始值的情况下，利用数值迭代算法逐渐逼近最终求解目标函数，得到 $\Delta \varphi (m)$ 的全局最优解。本文实验在输入数据序列中选取了强度较大的样本距离单元，并根据不同距离单元的相位方差对各样本距离单元进行加权，使含有多特显点的“高质量”样本在熵值收敛中起主导作用，进一步降低了杂波以及噪声等对算法的影响，同时提高了收敛速度，另外本文实验以变步长的梯度下降法寻找 $\Delta \varphi (m)$ 的值^[12]，进一步提高了迭代的计算速度，同时保证了最终的图像质量。

经过距离对准与相位校正后的数据可以表示为：

$\begin{split}S(t,{f_\eta }) = \!\!\!\!& \sigma ({f_\eta }) \cdot {\rm sin c}\left\{ {{π} B\left[ {t - \frac{{2R}}{c}} \right]} \right\}\\ & \cdot \exp \left[ {\frac{{ - {\rm j}4{π} R}}{\lambda }} \right]\end{split}$

(16)

(4) 利用方位向FFT将数据变回图像域，同时实现方位向压缩，得到聚焦后的结果。

3.2 参数估计方法

3.1节的步骤(3)中获得了每一个脉冲对应补偿的相位 $\Delta \varphi (n)$ ：

$\Delta \varphi (n) \approx \frac{{4{π} \Delta R({f_\eta })}}{\lambda }$

(17)

根据SAR成像理论，方位时间域与多普勒频域存在着一一对应的关系，因此斜距误差的表达式在方位时域与方位多普勒域具有近似相同的表达形式，将 $\Delta R(f_ {η} )$ 替换成第2节中分析得到的斜距误差表达式，可以得到：

$\begin{array}{l}\Delta \varphi (n) \approx \!\!\!\!\!\!\!\! &\frac{{4{π} }}{\lambda }\cdot A \cdot \cos \gamma \cdot \sin (\omega \eta + \varphi )\\ & \Big/ \frac{{4{π} }}{\lambda } \cdot A \cdot \cos i \cdot \sin (\omega \eta + \varphi )\end{array}$

(18)

通过对 $\Delta \varphi (n)$ 的正弦拟合可以得到相应的起伏运动幅度和周期等。

4 仿真分析与实验

为了验证上述分析的正确性和校正方法的有效性，下文首先对低轨高分辨率SAR进行仿真实验，接着将该方法用于TerraSAR-X的实际数据处理，并给出了实测结果。

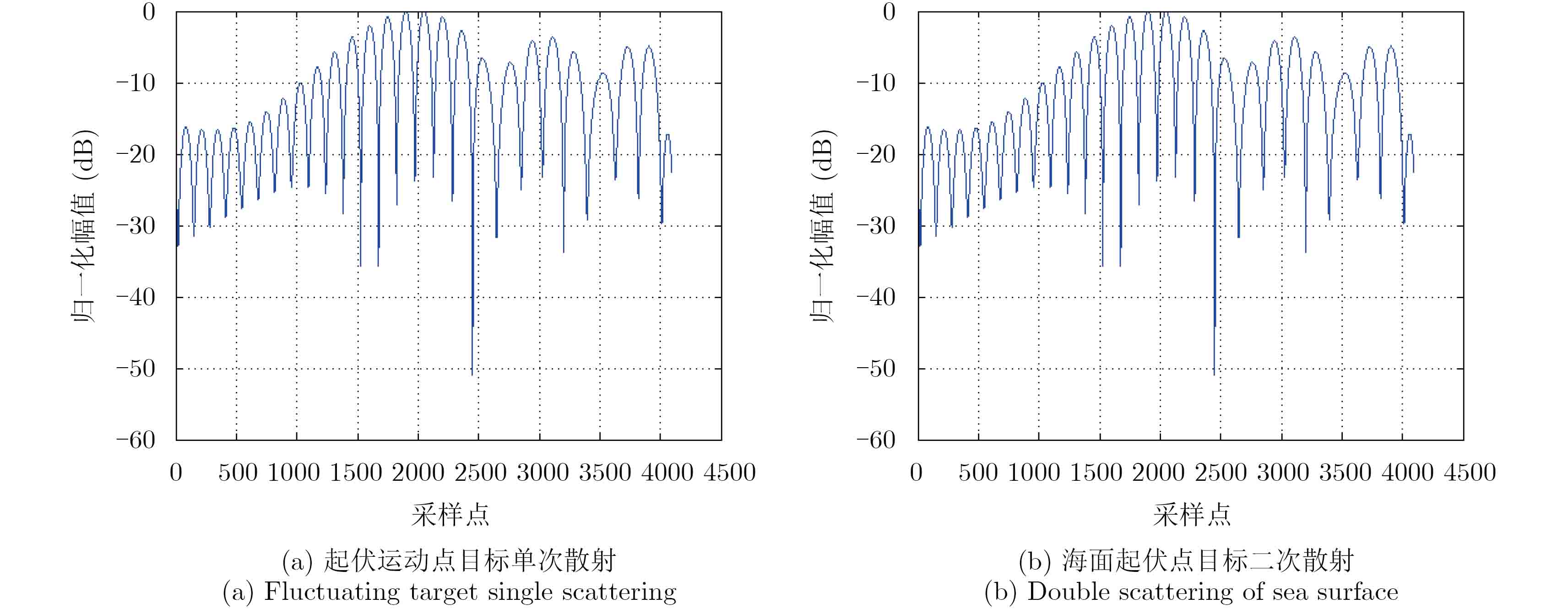
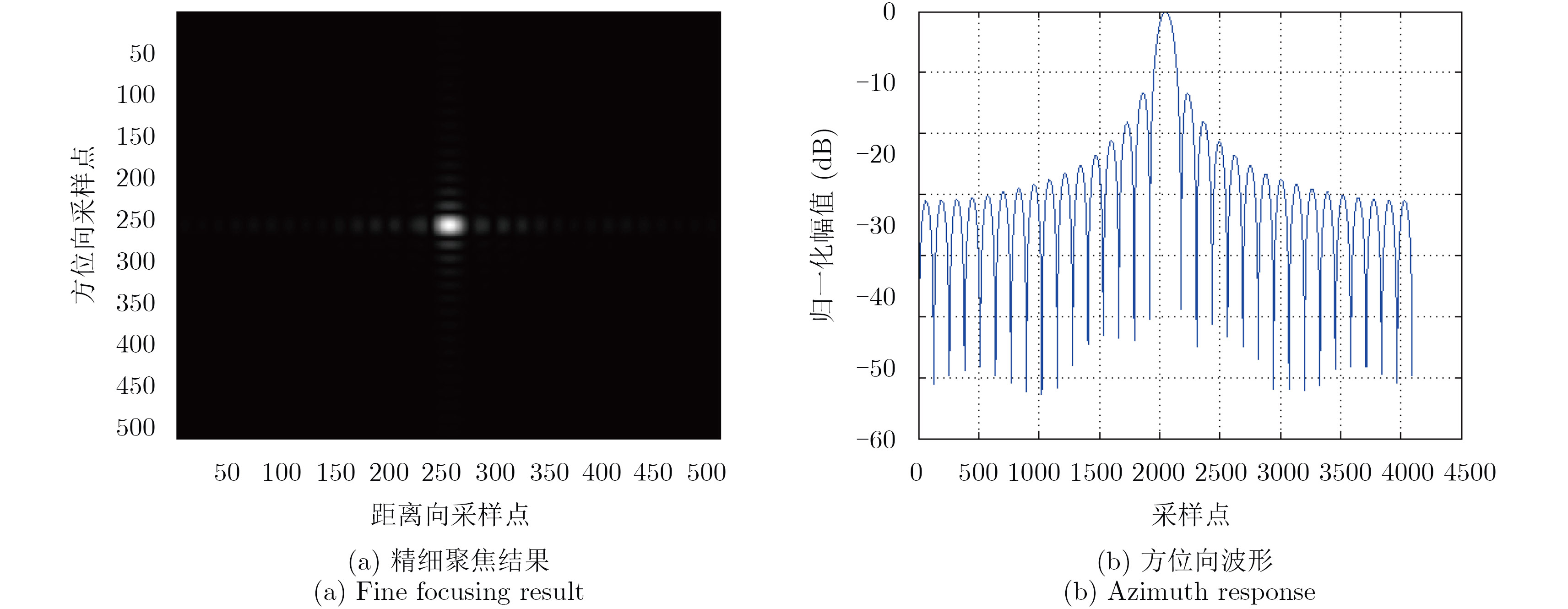
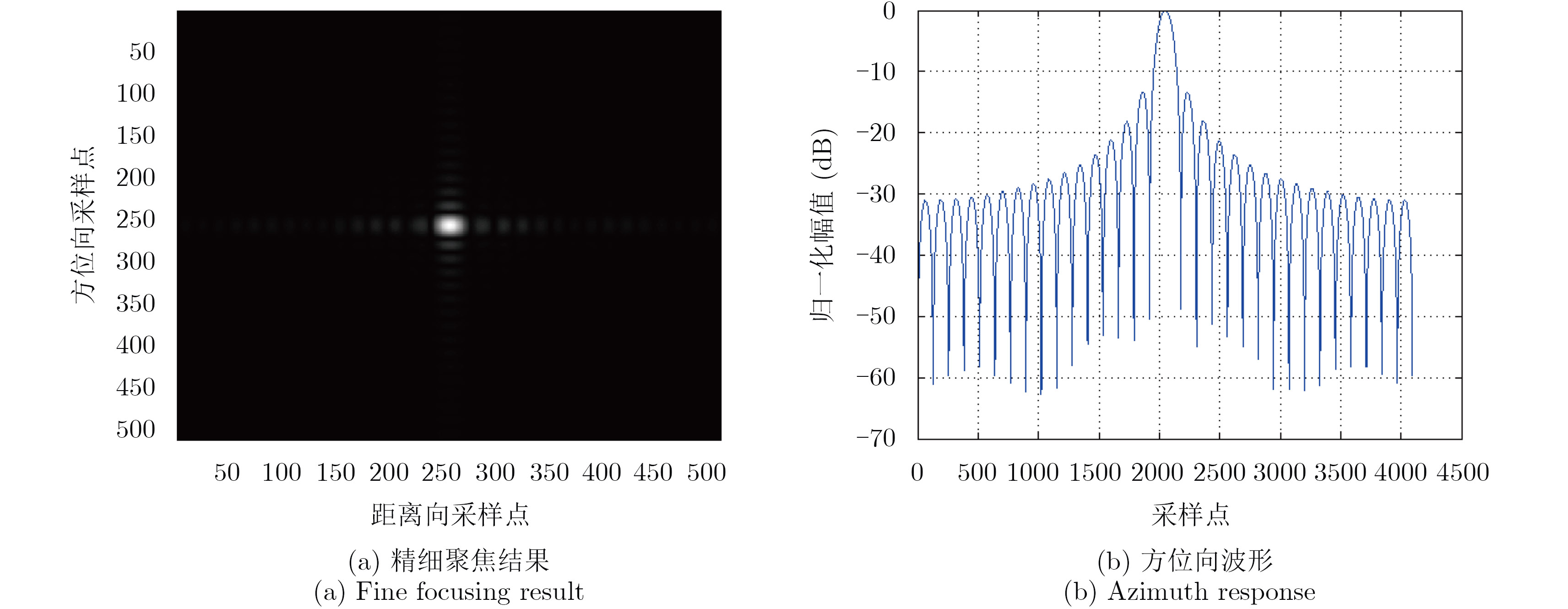
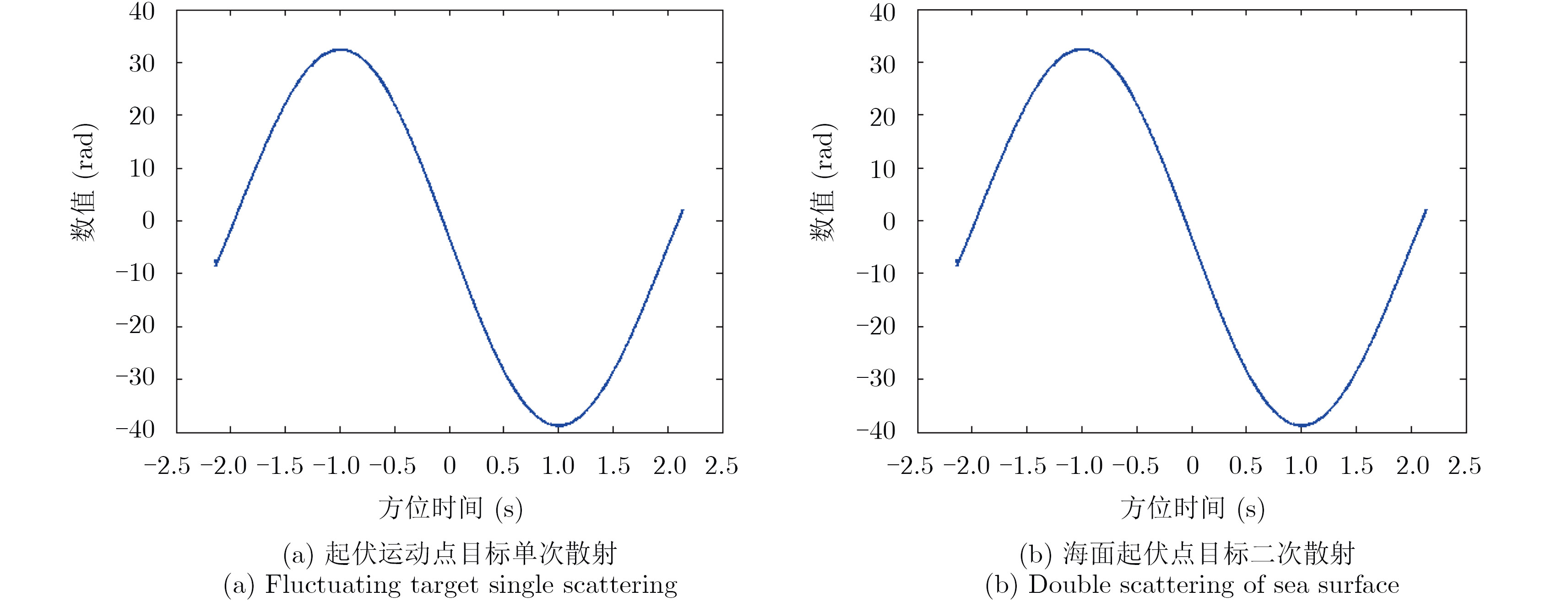
4.1 仿真实验

仿真系统参数如表1所示。根据近海岸海浪信息设置了3组起伏运动参数，分别为A=0.1 m, T_v=2.5 s;A=0.1 m, T_v=4 s和A=0.05 m, T_v=2.5 s。其中T_v=2$\pi $/$\omega $。起伏运动点目标单次散射成像结果如图4所示，海面起伏时点目标二次散射成像结果如图5所示。选取运动参数为A=0.1 m, T_v=4 s的两组成像结果做32倍插值，得到的方位向波形如图6所示，应用本文精细聚焦方法处理，两组结果的聚焦结果及对应方位向波形图分别如图7和图8所示，同时得到的相位补偿曲线如图9所示，参数估计结果及估计误差如表2所示。

由上述仿真结果可见，起伏运动会使成像结果在方位向出现原点目标的多重复制，进而形成线状散焦，散焦程度随起伏周期变大而减小，随起伏幅度变小而减小，这一结果与式(6)和式(12)的理论分析一致。两组散焦结果经过精细聚焦后的方位波形较理想，质量评估达标，从而验证了本文精细聚焦方法的正确性和有效性。两组参数估计结果都比较准确，估计误差较小，证明了本文参数估计方法的正确性和有效性。

4.2 实际数据处理结果

本文选取了TerraSAR-X旅顺地区1景SAR图像进行实验处理，该景图的相关参数如表3所示。

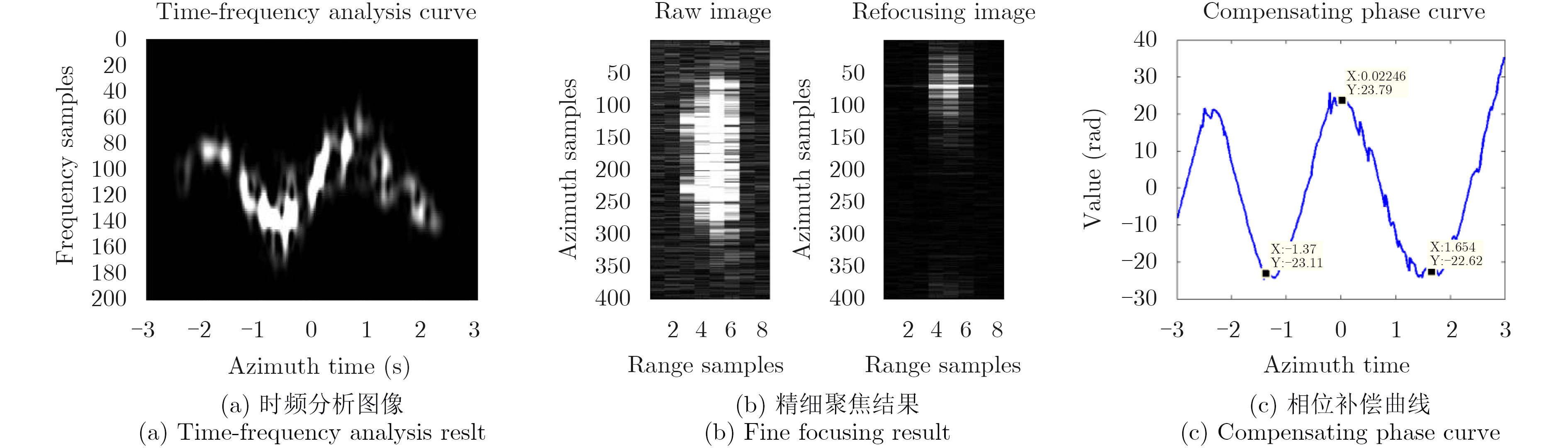
第1幅海岛近海岸SAR图像与对应的光学图像如图10(a)与图10(c)所示，可见海岛边呈须状散焦的亮线是拴在岸边的浮桶，由于海浪的作用存在起伏运动，其散焦特征与仿真结果相似。选取图10(a)中左下角右起第2条亮线做时频分析，其结果如图11(a)所示，可见散焦亮线方位向时频存在正弦调制的关系，对其应用本文的精细聚焦算法，其聚焦前后的对比结果如图11(b)所示，可见精细聚焦效果明显，补偿相位如图11(c)所示，其参数估计结果为：

$\begin{split}& A_{\rm e} = 0.14 \sim 0.25\;{\rm m}\\& T_{\rm e} = 2.8 \sim 3.5\;{\rm s}\end{split}$

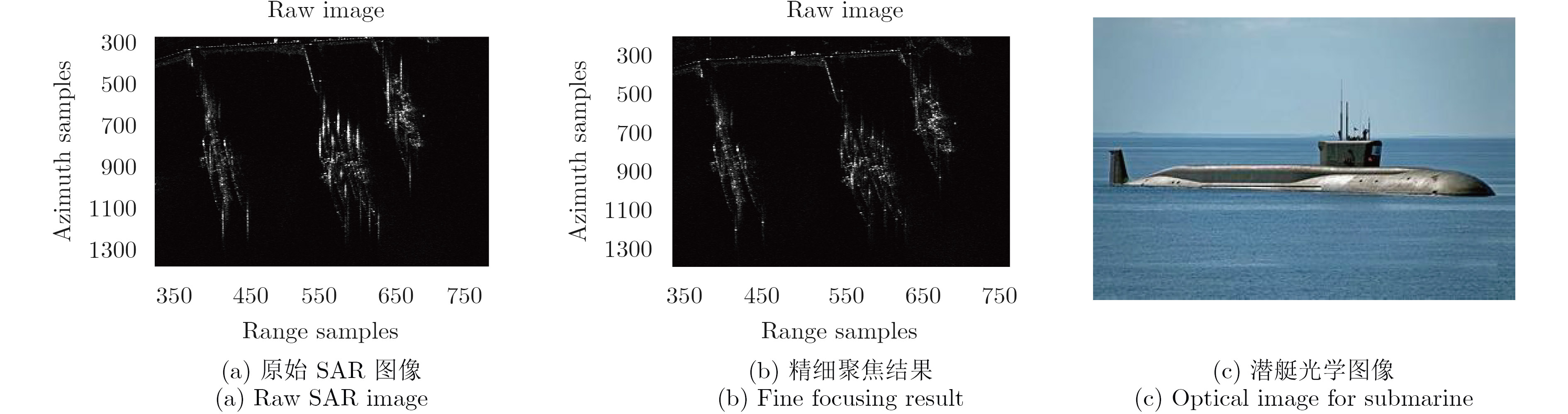
第2幅近海岸码头SAR图像如图12(a)所示，可见码头停靠的潜艇尾部有较整体更明亮的线状散焦，码头停靠的潜艇光学图如图12(c)所示，可见潜艇尾部的垂直翼与海面形成了1个二面角，潜艇尾部的二次散射较多，对该幅图像做精细聚焦处理的结果如图12(b)所示，可见聚焦效果明显，其起伏运动参数估计结果为：

$\begin{array}{l}A_{\rm e} = 0.15 \sim 0.25\;{\rm m}\\T_{\rm e} = 3.8 \sim 5.2\;{\rm s}\end{array}$

考虑到码头海浪的实际情况，两幅图像估计得到的参数都较为合理，证明了本文方法的准确性与有效性。

5 总结

本文对高分辨率星载SAR中目标起伏运动引入的误差进行了定量化分析，并仿真了其在SAR图像中的成像特点，提出了一种基于星载复图像数据进行运动误差补偿和精细聚焦处理的方法，同时估计得到目标的运动参数和海浪信息。仿真实验和TerraSAR-X港口区域实际数据实验验证了该方法的有效性和正确性。