1 引言

随着技术的发展和社会的进步，遥感观测中城市区域建筑物和其他人造设施的自动识别与重建变得日益重要，城区建筑3维模型可以广泛应用于城市规划与管理、旅游业、建筑业、灾害评估与防治等多个方面^[1]。传统SAR作为一种全天时全天候的遥感手段，在军事和民用多个方面获得了广泛的应用，但由于只具备方位向和距离向两维的分辨能力，已不能完全满足实际应用的需求。阵列干涉SAR技术^[2]是InSAR技术的延伸，通过在交轨向布放多个阵元形成天线阵列，具备了高程向分辨能力，同时提高了多个通道之间的相参性，保证相干测量精度，实现观测场景的高精度3维成像。

与传统的InSAR技术相比，阵列干涉SAR技术不仅能够获得场景的高程信息，还能获得场景散射点在高程向上的分布，对于高层建筑形成的叠掩区域依然具备3维成像能力^[3]，得到真实场景的不模糊3维成像结果。SAR 3维成像的概念自上世纪90年代提出以来，国内外进行了很多相关方面的研究，包括超分辨谱估计^[4]、压缩感知^[5]等3维成像算法的研究。2000年，Reigber等人首次完成了机载多基线SAR实验，实现了同一分辨单元内多个散射目标的定位^[6]。近年来，德国宇航中心(DLR)致力于TerraSAR-X的高分辨率SAR数据3维成像的应用与研究，并提出了一种基于压缩感知的称之为SL1MMER的算法，具有很强的超分辨能力^[7,8]。

然而这些方法大多只进行高程分辨，获得散射点在高程向的分布，由于星载TomoSAR数据的稀缺性，对于3维点云后处理这块的研究比较少。DLR朱晓香等有专门针对获取的SAR 3维点云进行后续处理的相关研究，提出了将经典的K-means聚类算法引入点云处理中，成功地对3维点云实现了聚类分析。但是K-means算法本身具备的缺点会影响聚类结果的准确性，具体结果将在本文的算法性能评估章节中比较。阵列干涉SAR系统阵元数目有限，基线长度较短，仅利用高程向超分辨方法得到的3维成像结果精度较差，建筑物轮廓不清晰，难以有效识别建筑物。针对上述问题，本文提出了一种基于高斯混合聚类^[9]的阵列干涉SAR 3维成像方法，在利用基于压缩感知的超分辨算法获得场景的原始3维点云后，对3维点云进行建筑物区域提取，利用高斯混合聚类算法对建筑物的各个平面进行识别，并利用系统参数进行SAR图像反演，从而得到最终的3维成像结果。在文章接下来的部分，本文给出了识别提取建筑物区域方法和3维点云聚类的性能分析，同时对于国内首次机载阵列干涉SAR数据进行处理，获得了真实建筑物的3维成像结果，验证了本文算法的有效性。

2 机载阵列干涉SAR 3维成像基础

星载SAR利用卫星重轨飞行来实现SAR系统多基线的获取，这样虽然可以获得较长的基线，但存在数据获取空间去相关和时间去相关比较严重等问题。不仅如此，在机载SAR系统中，重轨飞行的机载平台控制难以保证要求，多次航过耗费的时间成本和经济成本巨大。而机载阵列干涉SAR系统在交轨向上布置多个阵元，一次航过即可获取数据进行3维成像，在军事及民用观测任务中有着更为广阔的应用前景。

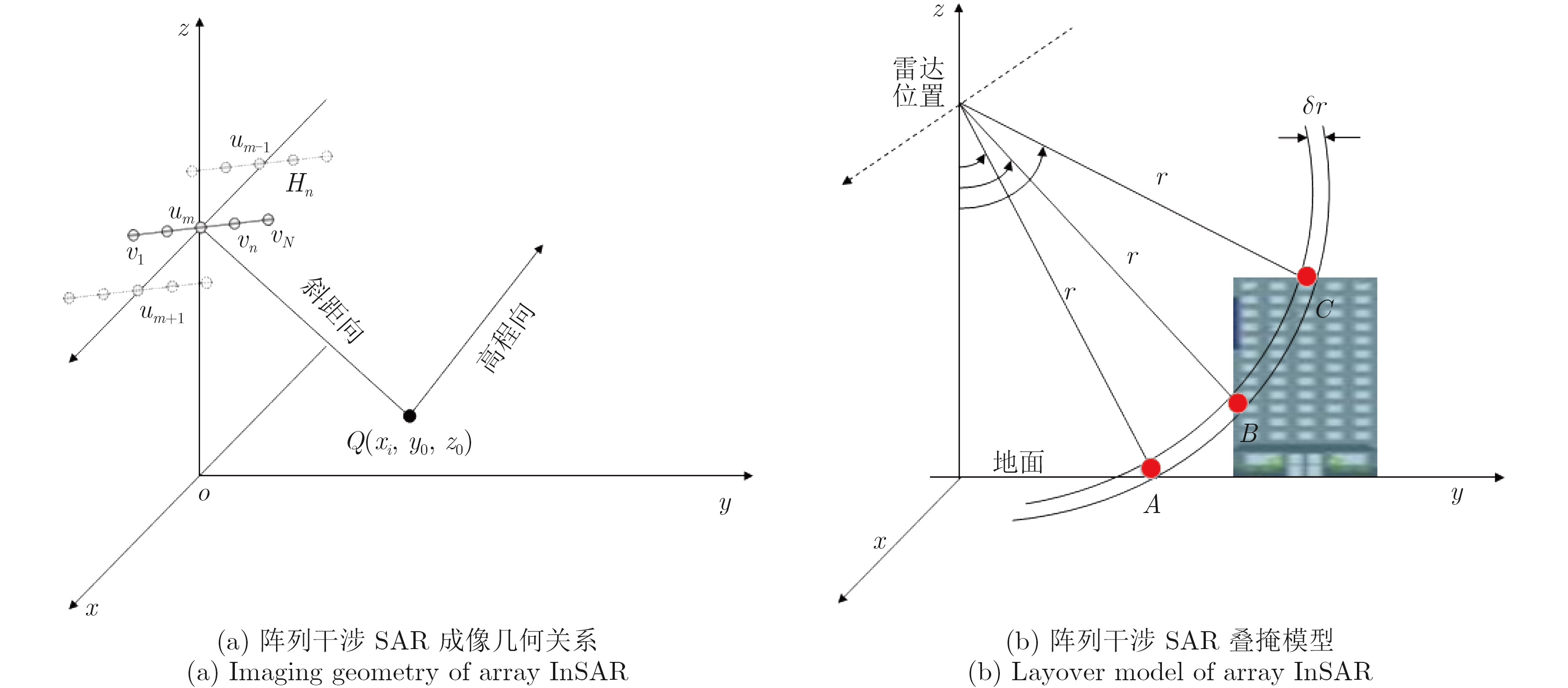
阵列干涉SAR成像几何示意图如图1(a)所示，假设飞机沿x方向作匀速直线运动，u_m表示第m个方位向时刻雷达的方位向位置，v_n表示第n个阵元的交轨向位置，H_n表示第n个阵元的高度向位置。其中，方位向和距离向(斜距向)两维我们采取常规的SAR成像算法，在高程向即图1(a)中与斜距垂直的方向，同一个分辨单元的信号是高程向多个散射点信号回波的叠加，如图1(b)所示，单个方位斜距分辨单元的测量值里包含了3个不同散射点的后向散射信号，这是由于这3个散射点距离SAR传感器有着相同的斜距，所以混叠在了同一个分辨单元里。利用配准好的N幅SAR图像，我们可以对每一个分辨单元沿着高程向重建后向散射系数分布的情况。

在这N个配准好的接收天线处，第n幅图像的特定分辨单元的复数值可以认为是真正的后向散射信号沿着高程向的积分^[10]，通常用下面的式子来表示：

${g_n} = \int\limits_{\Delta s} {\gamma (s)\exp ( - {\rm j}2{π} {\xi _n}} s){\rm{d}}s$

(1)

其中 $\Delta s$ 代表高程向的范围， ${\xi _n}$ 是沿着高程向的空间频率， $\gamma (s)$ 是沿着高程向在s位置的后向散射系数。

考虑到噪声，系统高程向上的聚焦模型可以简化为

${g} = {R}{γ} + {ε} $

(2)

其中g是长度为N的观测向量，R的形式为 ${R_{n \times l}} = \exp ( - {\rm j}2{π} {\xi _n}{s_l})$ ，是一个 $N \times L$ 的匹配矩阵(部分傅里叶变换矩阵)， ${γ} $ 是以 ${s_l}(l = 1,·\!·\!·,L)$ 在高程向上均匀采样的 $\gamma (s)$ , ${ε} $ 为噪声向量。由于 $N < < L$ ，所以式(2)的求解本质上是一个欠定方程组。理论上，L₀范数的最小化是对这个问题的最准确的解决方法，然而困难的是这是一个NP-hard问题。在许多情况里，L₁范数的最小化等价于L₀范数的最小化，从而可以利用基于压缩感知的方法来得到此方程组的结果。这样我们可以用下面的等式描述这个数学问题^[11]：

$\min {\left\| {γ} \right\|_1}\;\;{\rm{s}}{\rm{.t}}.{g} = {R} \cdot {γ} $

(3)

它可以通过岭估计来估计这个等式：

$\hat {γ} = \arg \mathop {\min }\limits_{γ} \{ \left\| {{g} - \left. {{R}{γ} } \right\|} \right._2^2 + {\lambda _K}{\left\| {γ} \right\|_1}\} $

(4)

其中 ${\lambda _K}$ 是根据噪声情况调节的一个超参数，可以分解为信号加上罚函数。罚函数的程度由 ${\lambda _K}$ 来控制。一般来说，信噪比较低时，需要选择相对较小的 ${\lambda _K}$ ，而信噪比较高时，需要选择较大的 ${\lambda _K}$ ，过低的信噪比会严重影响超分辨算法高程向散射点重构的性能。

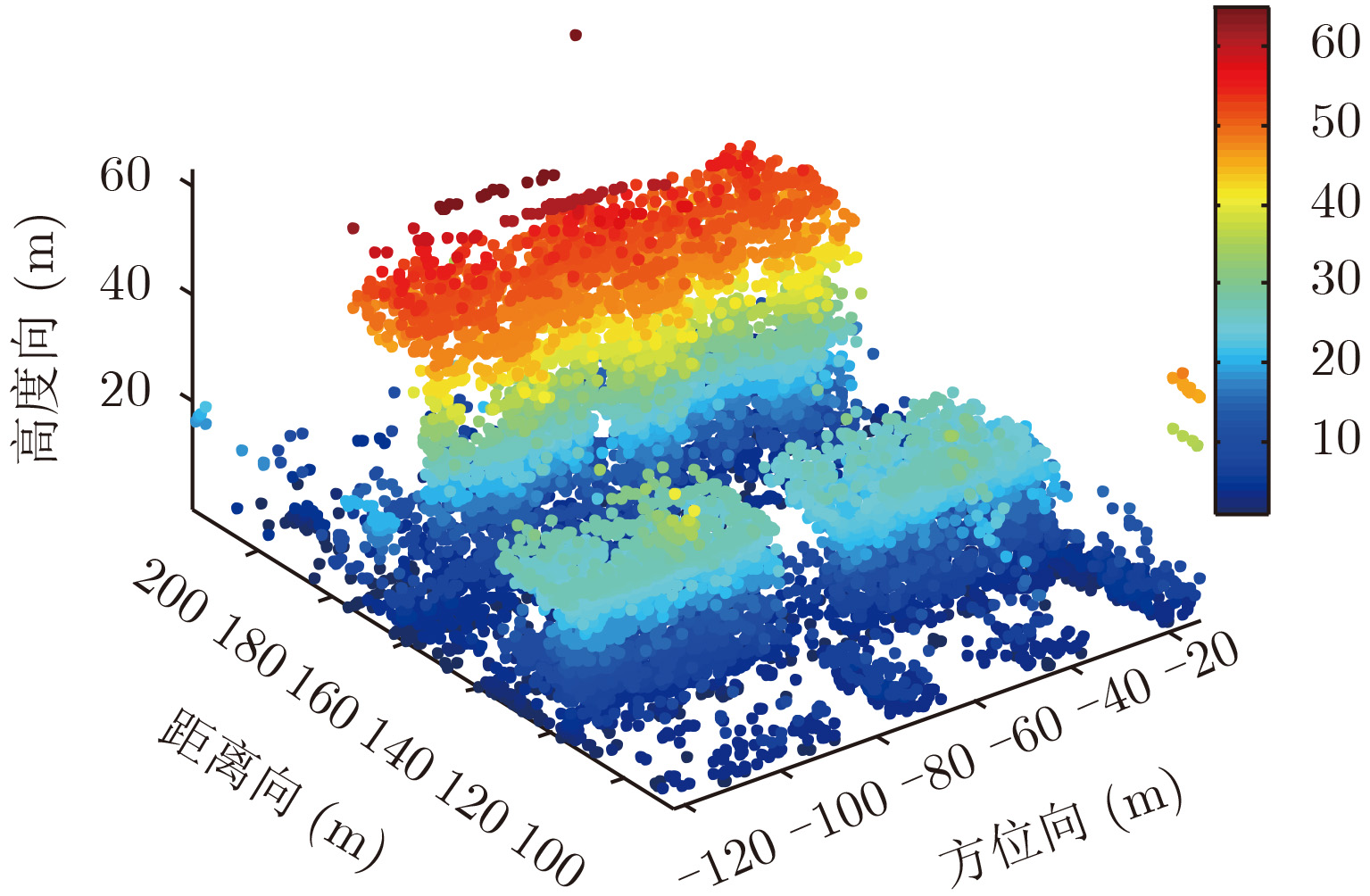
结合上述理论基础，本文提出了一种新的3维成像算法流程，Google Earth上观测场景的光学照片如图2所示，可以作为后期3维成像结果的参考。在对多幅SAR复图像进行如上所述的高程向分辨成像后，并进行坐标转换，得到如图3所示的观测场景的原始3维点云(其中距离向为地距向)，然后进行建筑物区域自动识别提取与聚类，将叠掩的区域分开各自单独反演获得对应SAR图像，完成地形融合与拼接后可以获得最终的3维成像结果。

3 基于高斯混合聚类的3维成像方法

基于上一节讨论的思想，本文提出了一种基于高斯混合聚类的阵列干涉SAR 3维成像方法，其主要步骤如下：

步骤1  对阵列干涉SAR多个通道的2维复图像进行图像配准、幅度校正和相位校正，从而满足观测区域3维成像的基本要求^[12]。

步骤2  利用基于压缩感知的超分辨算法对观测区域进行高程向成像，获得观测区域的原始3维点云分布图^[13]。

步骤3  将3维点云垂直投影到方位距离平面，以固定窗口大小进行分块，计算每个窗口的点云密度，密度超过设定阈值的区域提取出来，即为建筑物部分有效点云。

步骤4  利用点云的空间3维位置信息、散射点幅度以及相位信息，采用高斯混合聚类的方法对提取出的建筑物点云进行分类，得到不同建筑物各自单独的散射平面。

步骤5  对于上一步聚类得到的建筑物各个平面的点云，利用阵列干涉SAR系统参数对每一个平面进行反演，得到各个平面的SAR图像，将步骤6中3维点云剔除建筑物点云的余下部分反演得到整个地面的SAR图像。

步骤6  将上述获得的结果进行融合和拼接^[14]，最终得到整个观测区域的3维成像结果。

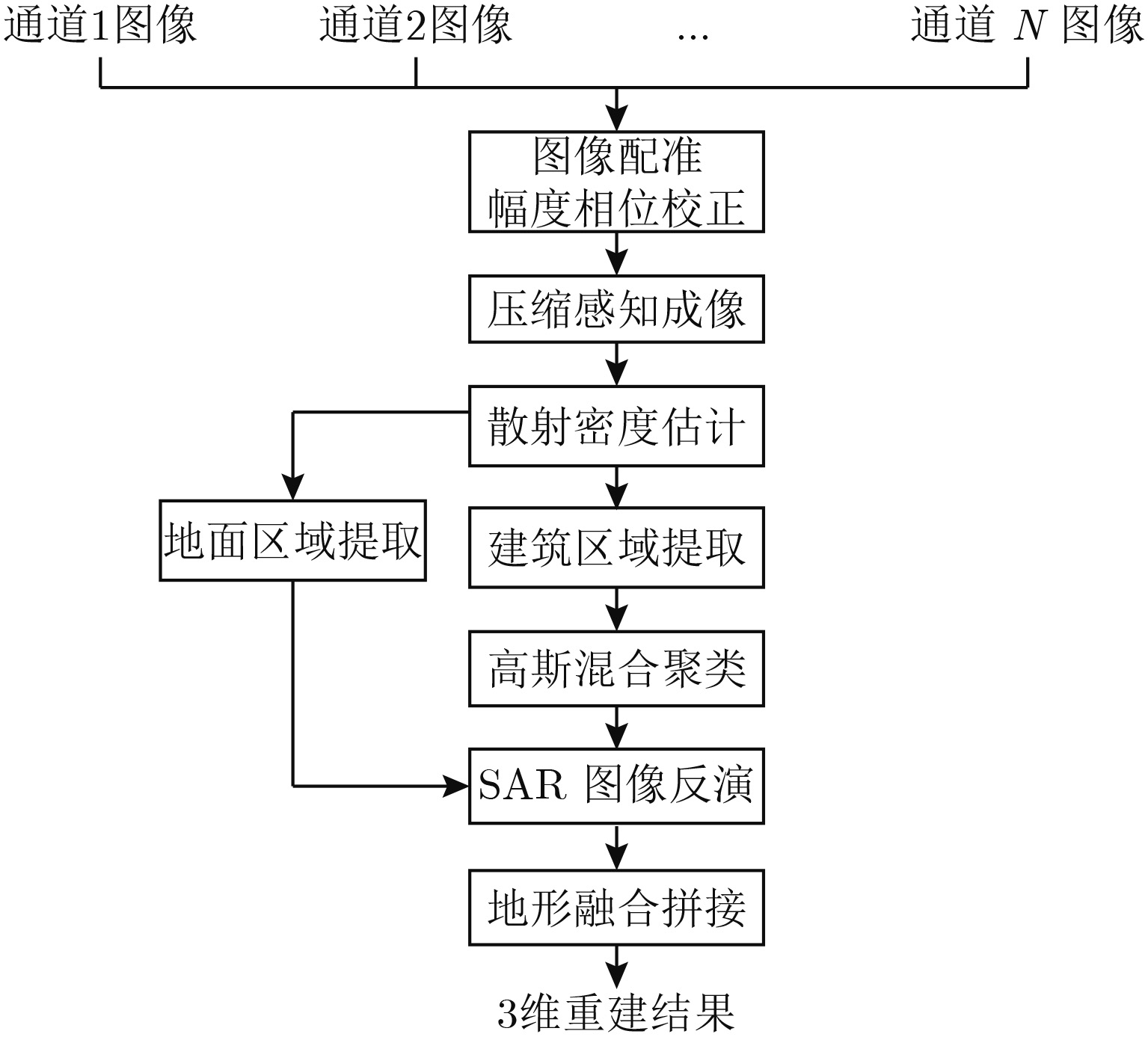
综合以上处理过程即可实现观测场景的3维成像，该算法流程图如图4所示。

上述处理过程中步骤1和步骤2相关研究较多，可以参考文献[8]、文献[12]、文献[13]的算法进行处理，步骤5比较容易实现，步骤6可以参考文献[14]进行处理，对于步骤3和步骤4，下面进行详细的讨论。

3.1 建筑物点云提取

3维点云中建筑物部分的有效识别与提取是建筑物3维重建中必不可少的一步。在LiDAR点云处理中，通常的做法是首先通过预滤波、形态滤波^[15]或者梯度分析^[16]等方法来计算数字地面模型(Digital Terrain Model, DTM)，结合LiDAR点云提供的数字表面模型(Digital Surface Model, DSM)，利用DSM和DTM相减可以得到标准化的表面模型(Normalized DSM, NDSM)，提取出3维点云中非地面部分的散射点^[17]，再利用一些几何特征，比如地表模型的偏差、高度测量、坡度变化等，最终提取出建筑物的散射点。

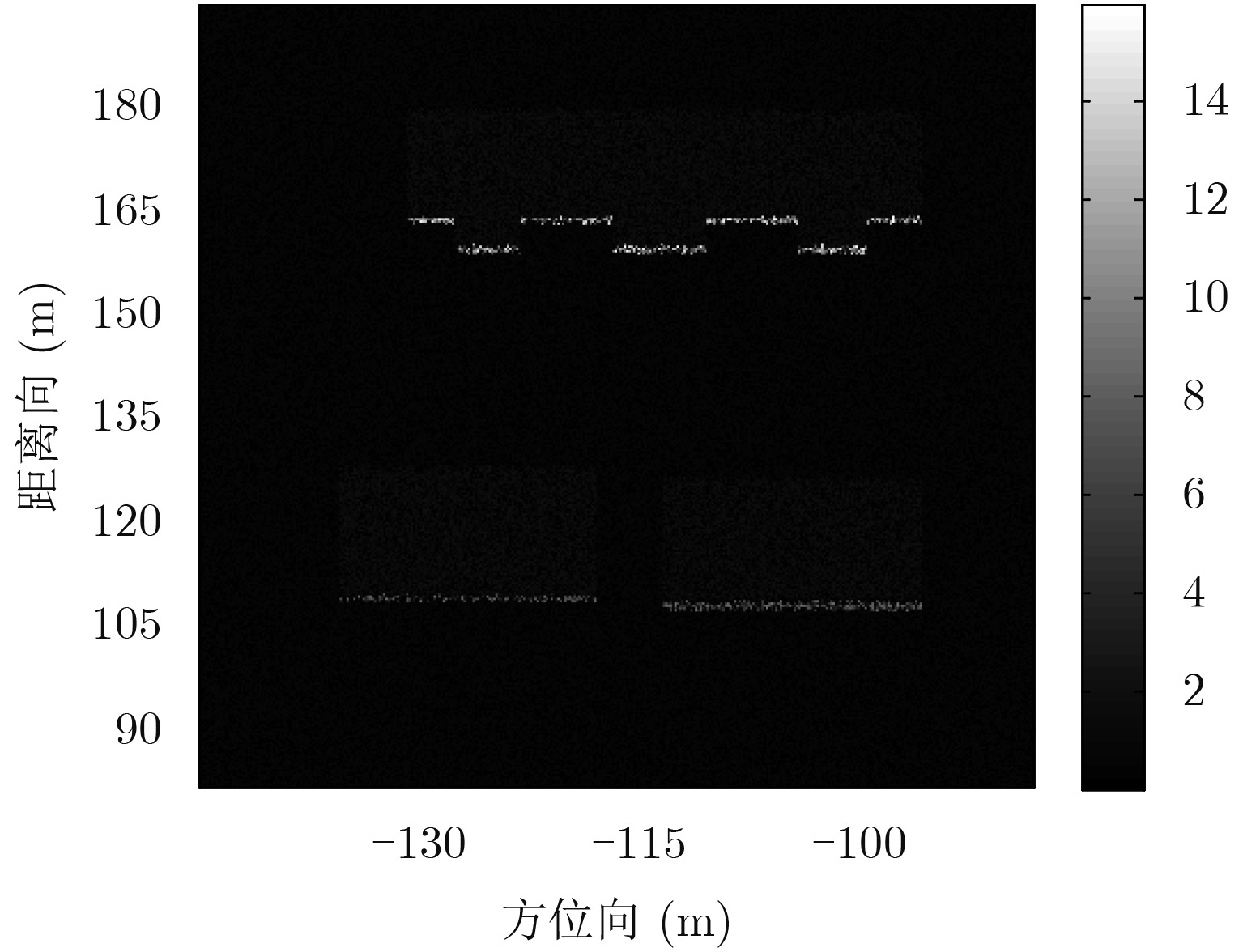
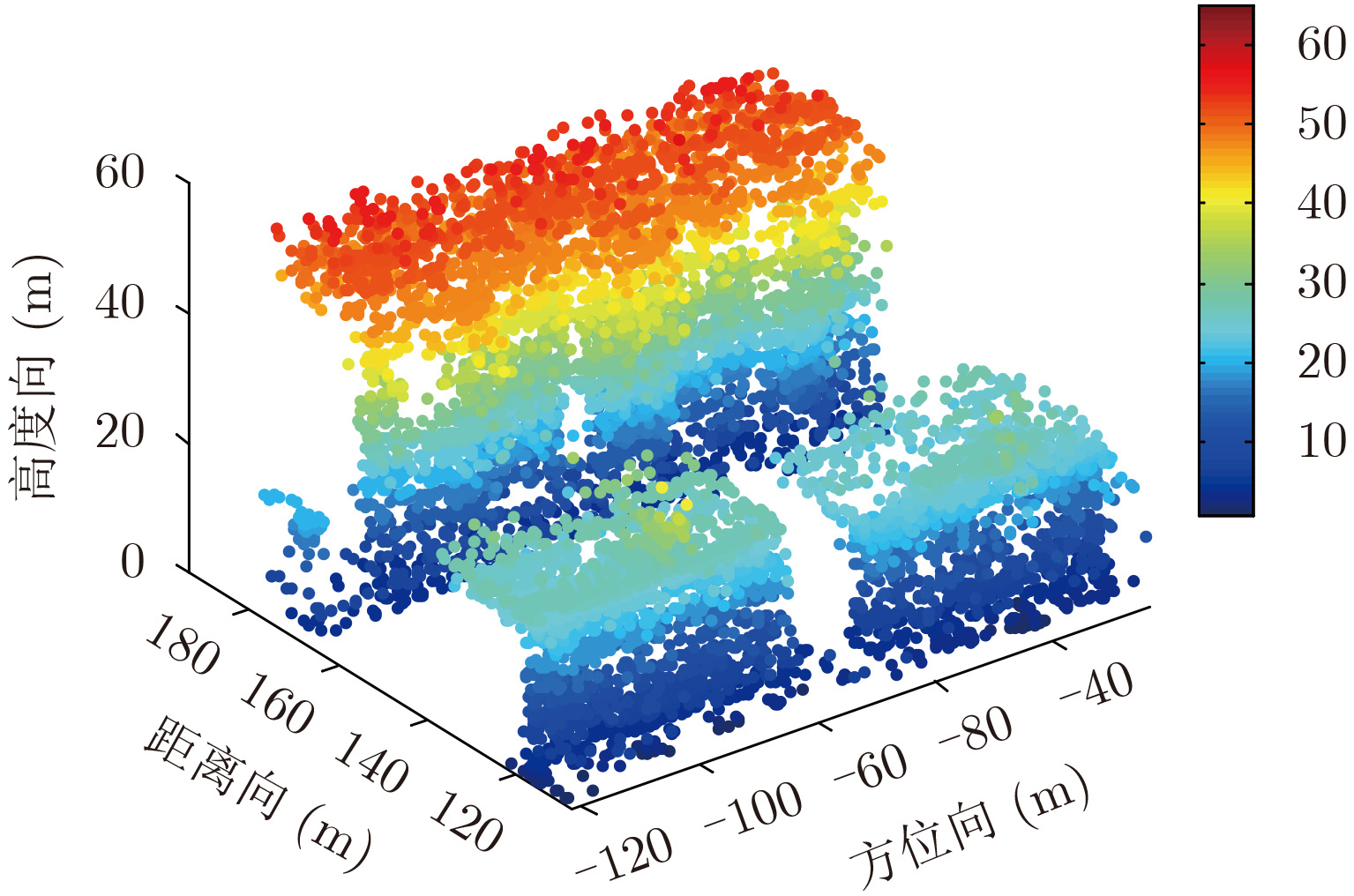
本文采取的方法是将观测区域的3维点云垂直投影到方位距离平面上，通过设定一定的阈值，计算方位距离平面的散射点密度来识别属于建筑物的区域并提取出来，这个方法适合于未做任何处理的原始3维点云。我们可以选择不同大小的窗口，对观测区域进行划分，计算每一个窗口内散射点的数目，图5即为选定参数下整个观测区域的散射点密度分布图。而在阵列干涉SAR的侧视模式下，垂直于地面的建筑或者人工设施的散射点密度会远远高于地面区域，而密度的大小由建筑物的高度决定，如此就成功的识别并提取了建筑物的有效点云，提取出的建筑物区域如图6所示。

3.2 基于SAR 3维点云的高斯混合聚类

高斯混合模型是多个单高斯分布的线性组合，式(5)表示的是K个高斯分布组合表示的高斯混合密度函数。其中 ${{π} _k}$ 表示各个高斯分布的加权系数， ${\mu _k}$ 和 ${\sigma _k}$ 表示各个高斯分布的均值和方差。公式是单高斯分布的表达公式，式中d为特征向量x的维度，μ为均值，δ为特征向量的协方差矩阵。

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! p({x}) = \sum\limits_{k = 1}^K {{{π} _k}{N}(} {x}\left| {{\mu _{k,}}{\sigma _k})} \right.$

(5)

$\begin{aligned}{N}({x};{μ} ,{δ} ) = & \frac{1}{{\sqrt {{{(2{π} )}^d}\left| {δ} \right|} }}\\& \cdot \exp \left\lfloor { - \frac{1}{2}{{({x} - {μ} )}^{\rm T}}{{δ} ^{ - 1}}({x} - {μ} )} \right\rfloor \end{aligned} $

(6)

基于SAR复图像的特性，本文所选取的特征向量为5维向量，包括散射点的3维空间位置、幅度及相位信息，因为位于同一建筑的同一散射平面的散射点空间位置会更加接近，幅度趋向于同一量级，相位呈现平坦连续变化的特征。为了更好地进行聚类，需要对子类的个数进行判定。本文采用了BIC准则^[18]来进行最适合分类数据集的聚类个数的估计，使BIC值达到最小的数值即为最优的聚类个数估计。

对于高斯混合模型系数的确定，本文采用EM算法^[19]来进行。高斯混合聚类的对数似然函数 $L({x}\left| {{\mu _{k,}}{\sigma _k})} \right.$ 为：

$L({x}\left| {{\mu _{k,}}{\sigma _k})} \right. = \sum\limits_{i = 1}^N {\log \left\{ {\sum\limits_{k = 1}^K {{{π} _k}{N}(} {x}\left| {{\mu _{k,}}{\sigma _k})} \right.} \right\}} $

(7)

为了确定高斯混合模型系数，需要进行最大似然估计，步骤如下：

(1) 估计数据由每个高斯分布生成的概率：对于每个数据x_i来说，它由第k个高斯分布生成的概率为：

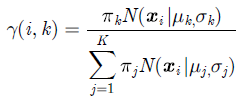
(8)

由于式子里的 ${\mu _k}$ 和 ${\sigma _k}$ 也是需要我们估计的值，我们采用迭代法，在计算 $\gamma (i,k)$ 的时候我们假定 ${\mu _k}$ 和 ${\sigma _k}$ 均已知，取上一次迭代所得的值(或者初始值)作为估计对象。

(2) 估计每个高斯分布的参数：现在我们假设上一步中得到的 $\gamma (i,k)$ 就是正确的“数据x_i由第k个高斯分布生成的概率”，集中考虑所有的数据点，现在实际上可以看作第k个高斯分布生成了 这些点。由于每个部分都是一个标准的高斯分布，可以很容易分布求出最大似然所对应的参数值：

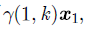
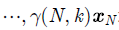
$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {{μ} _k} = \frac{1}{{{N_k}}}\sum\limits_{i = 1}^N {\gamma (i,k){{x}_i}} $

(9)

${\sigma _k} = \frac{1}{{{N_k}}}\sum\limits_{i = 1}^N {\gamma (i,k)({{x}_i} - {{μ} _k})} {({{x}_i} - {{μ} _k})^{\rm T}}$

(10)

其中 ${N_k} = \displaystyle\sum\nolimits_{i = 1}^N {\gamma (i,k)} $ ，并且 ${{π} _k}$ 也顺理成章地可以估计为 ${N_k}/N$ 。

(3) 重复迭代前面两步，直到似然函数的值收敛为止。

4 实验结果与性能评估

我们此次利用机载阵列干涉SAR系统对某一城市区域进行观测，工作模式为2发8收，在交规向具有16个相位中心，相邻两个阵元中心间距为0.084 m，其他系统参数如表1所示。

4.1 建筑物提取性能评估

为了评估建筑物提取步骤的质量，本文采取了一种逐点比较的方法，提取出的建筑物散射点和参考建筑物进行对比，完成性能评估。

参考建筑物

实际实验中我们并没有代表真正建筑物区域的准确数据，所以在建筑物散射点提取有效性的精确评估是无法做到的。参考文献[14]的参考建筑物标准，根据阵列干涉SAR系统的参数，类似地我们假设距离建筑轮廓线中心2个像素内的点为有效的散射。

评估准则

原始3维点云的输入中，所有的点被假设分为两类：建筑物散射点或者非建筑物散射点。提取出来的建筑物散射点属于参考建筑物的定义为T_p，不属于参考建筑物的定义为F_P。类似地，属于参考建筑物的散射点被检测为非建筑物散射点的定义为F_N。建筑物散射点提取的性能可以参考以下的评估准则：

${\rm Completeness}(\% ):{\rm comp} = 100*\left(\frac{{{T_{\rm{p}}}}}{{{T_{\rm{p}}} + {F_{\rm{N}}}}}\right)$

(11)

$\!\!\!\!\!\!\!\!\!\! {\rm Correctness}(\% ):{\rm corr} = 100*\left(\frac{{{T_{\rm{p}}}}}{{{T_{\rm{p}}} + {F_{\rm{P}}}}}\right)$

(12)

$\begin{split}\!\!\!\!\!\!\!\, {\rm Quality}(\% ):Q & = \frac{{{\rm comp}*{\rm corr}}}{{{\rm comp} + {\rm corr} - {\rm comp}*{\rm corr}}}\\ & = \frac{{{T_{\rm p}}}}{{{T_{\rm p}} + {F_{\rm P}} + {F_{\rm N}}}}\end{split}$

(13)

完整度Completeness显示了算法检测建筑物散射点的完成比例，而正确率Correctness显示了正确检测的概率，而质量评价Quality对于选定窗口和阈值参数的提取性能是一个至关重要的参数。

窗口大小GA和阈值TH的关联性

两个参数影响提取出的建筑物散射点个数：窗口大小GA和阈值TH。为了评估这两个参数对于提取阶段的影响，本文进行了下列不同数值GA和TH的实验，GA={0.1*0.1, 0.2*0.2, 0.3*0.3, 0.4*0.4, 0.5*0.5} m², TH={1, 2, 3, 4, 5, 6} 点数/dm²。

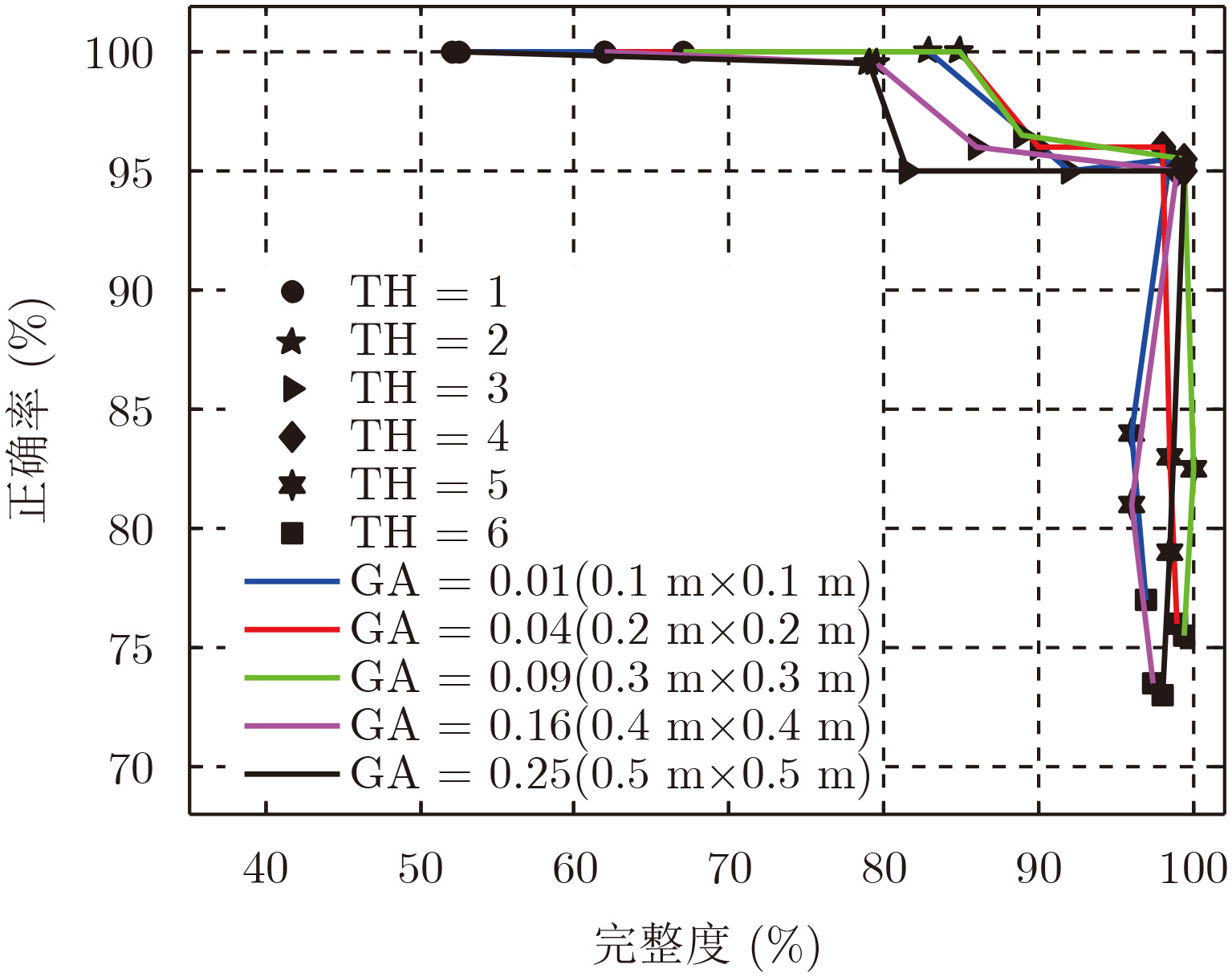
为了评估提取建筑物散射点算法的性能，本文给出了不同的窗口和阈值下完整度和正确率的相关变化曲线，从而可以在调整参数的基础上，权衡完整度和正确率的关系，选择最适合的窗口阈值参数。图7显示了不同TH和GA下的评估结果，显而易见TH的值越小，完整度越高，而TH的值越大，则F_P的值会减少，从而导致正确率越高。窗口的散射点密度越高，属于建筑物的可能性越大。表2给出了在上述的6组TH和5组GA下各自提取散射点的质量评价Q。可以看出，在TH=3, GA=9 dm²下，提取散射点的性能是最高的，达到了94.82%，在图7中观察到这组参数下的完整度和正确率也是综合起来最优的，分别达到了99.95%和97.12%。

基于上述的讨论，窗口的大小被设置为9 dm²，通过设置3点/dm²的阈值，需要说明的是，这组参数是在本文的机载阵列干涉SAR系统参数和特定观测场景下得到的最优估计，当系统参数和观测场景变化时，最优的阈值TH和窗口GA也会发生变化。在本次飞行实验中，观测条带近距端和远距端相差不算太远，建筑物点云的密度也基本相同，因此本次实验观测的城市区域都可以选择本文中的窗口阈值组合作为选择标准，不会造成太大的偏差，如果追求更加准确的最优化组合，可以重新按照上述的步骤进行参考建筑点云的标准制定和最优窗口阈值组合的筛选。不过要指出的是，当处理其他飞行架次数据以及阵列干涉SAR系统参数发生变化时，比如波段、载机高度、下视角等发生变化时，重新进行最优窗口阈值组合的筛选是十分有必要的。

4.2 聚类性能评估与结果

上一步中提取出的建筑物散射点需要进一步聚类为对应的各个单独的平面点云，包括建筑物侧面和建筑物楼顶等平面。为了验证BIC准则下选取子类个数k的性能，本文计算了不同子类个数下偏差度的曲线^[20]。

本文定义了D_r作为子类r中的点的平均偏差距离，如式(14)所示：

${D_{{r}}}{\rm{ = }}\sum\limits_{i = 1}^{{n_r}} {\frac{{{d_i}}}{{{n_r}}}} $

(14)

其中，n_r为子类r中的散射点数目，d_i为子类r中第i个点到聚类中心的欧式距离。则对于子类个数k的偏差度可以定义为：

${I_k}{\rm{ = }}\sum\limits_{r = 1}^k {\frac{{{D_r}}}{k}} $

(15)

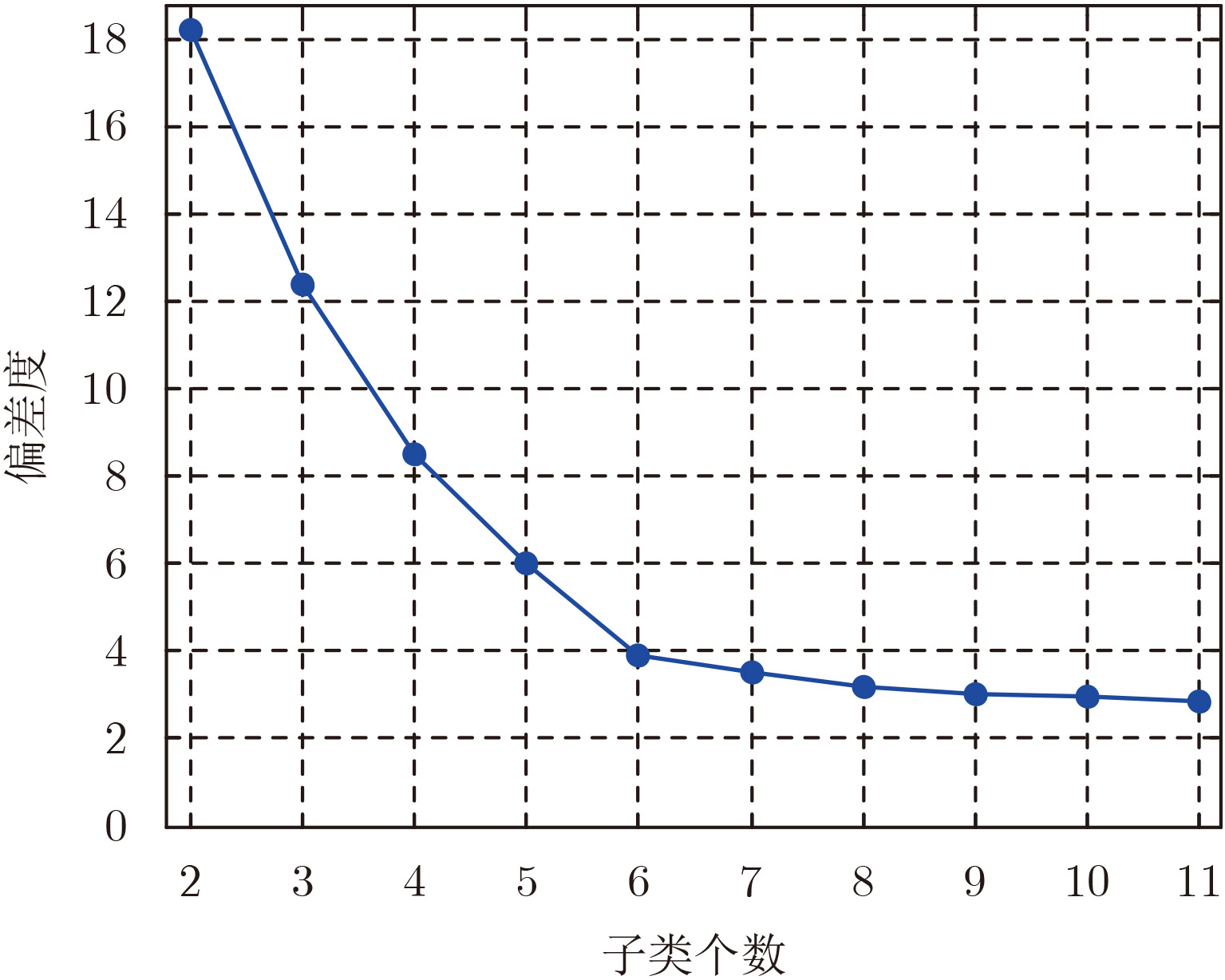
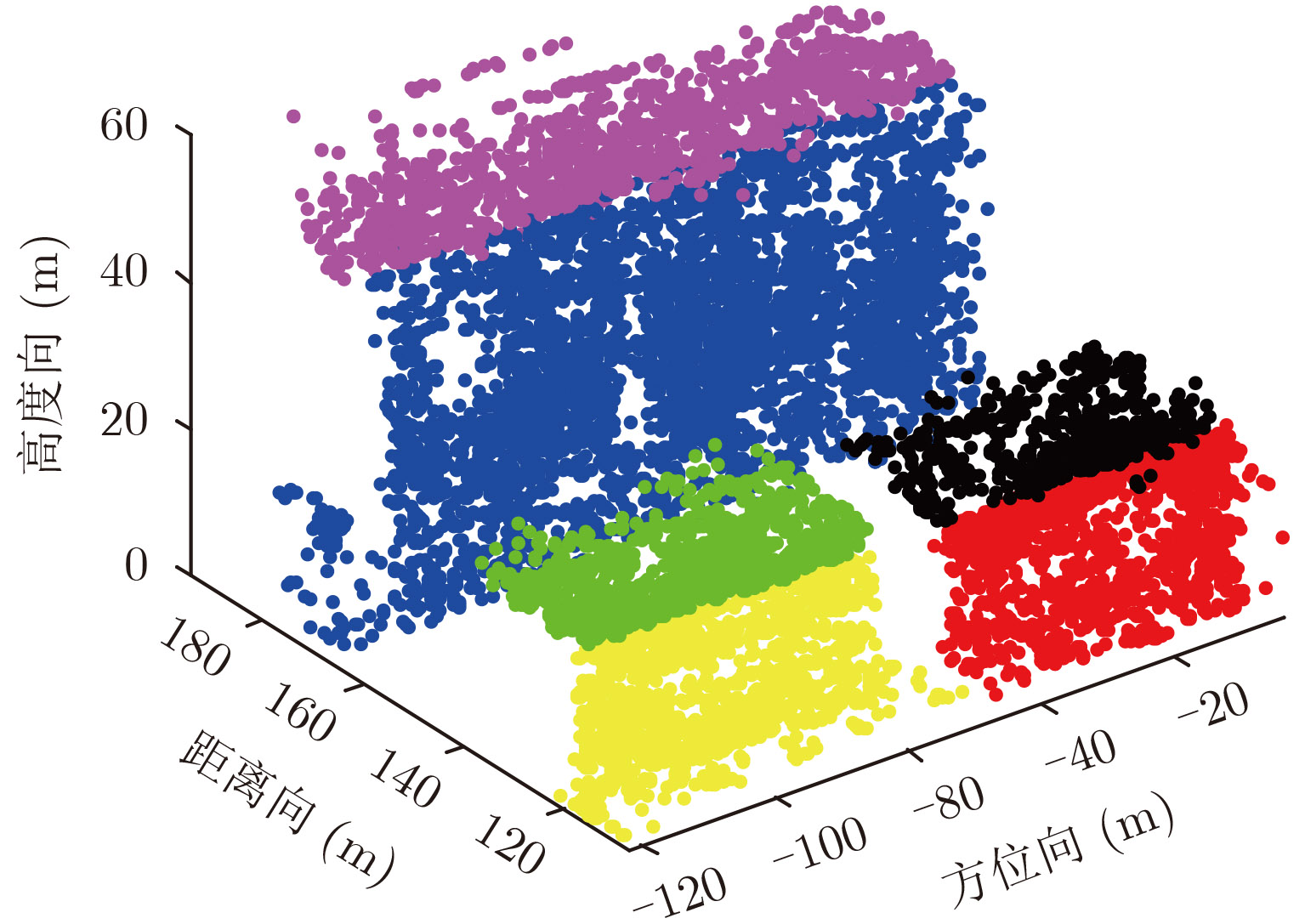
偏差度I_k通常会先随着子类个数k的增加而显著降低，然后继续增加则会趋于稳定，曲线的拐点处对应的子类个数k可以认为是对子类个数的最优估计。在上述思想下，本文计算了不同子类个数下的偏差度，结果如图8所示，可以看出k取6时曲线到达了拐点，偏差度趋于稳定。图9为最终得到的建筑物不同部分的聚类结果，可以看到将整个建筑物群分成了6个部分，分别为3幢楼各自的侧面和楼顶部分，分割的区域符合建筑物本身的结构特性，每种颜色的散射点对应一个单独的子类，即属于同一个平面的点云。可以看出，建筑物点云在高斯混合聚类的方法下被分成了6个子类，分别对应这3幢建筑各自的楼体侧面和楼顶区域，符合下一步SAR图像反演的要求。

为了对比其他3维点云后处理方法与本文算法的区别，本文给出了参考文献[14]中提出的经典聚类算法K-means算法和本文算法进行对比。

首先，K-means算法需要事先设定聚类的数目，无法自适应调整聚类个数。本文采用了BIC准则进行聚类个数的最优数目估计，表达式可以写为：

$\hat k = \mathop {\arg \min }\limits_k \left\{ n\ln \frac{{\rm SSE}}{n} + k\ln n \right\} $

(16)

其中，SSE是估计模型的残差平方和，n为点云数目，k为聚类个数，对于使得BIC值最小的k即为聚类个数的最优估计。

其次，K-means算法需要事先指定初始聚类中心，进行迭代处理，当初始聚类中心选取不合适时，迭代时可能会陷入局部最优解，聚类的结果不能满足要求。因此，K-means的聚类准确率和聚类效果不如高斯混合聚类，并且在高斯混合聚类的方法中，本文在特征向量的选取中引入了SAR图像复数据特有的幅度和相位特征，进一步提升了聚类的性能。

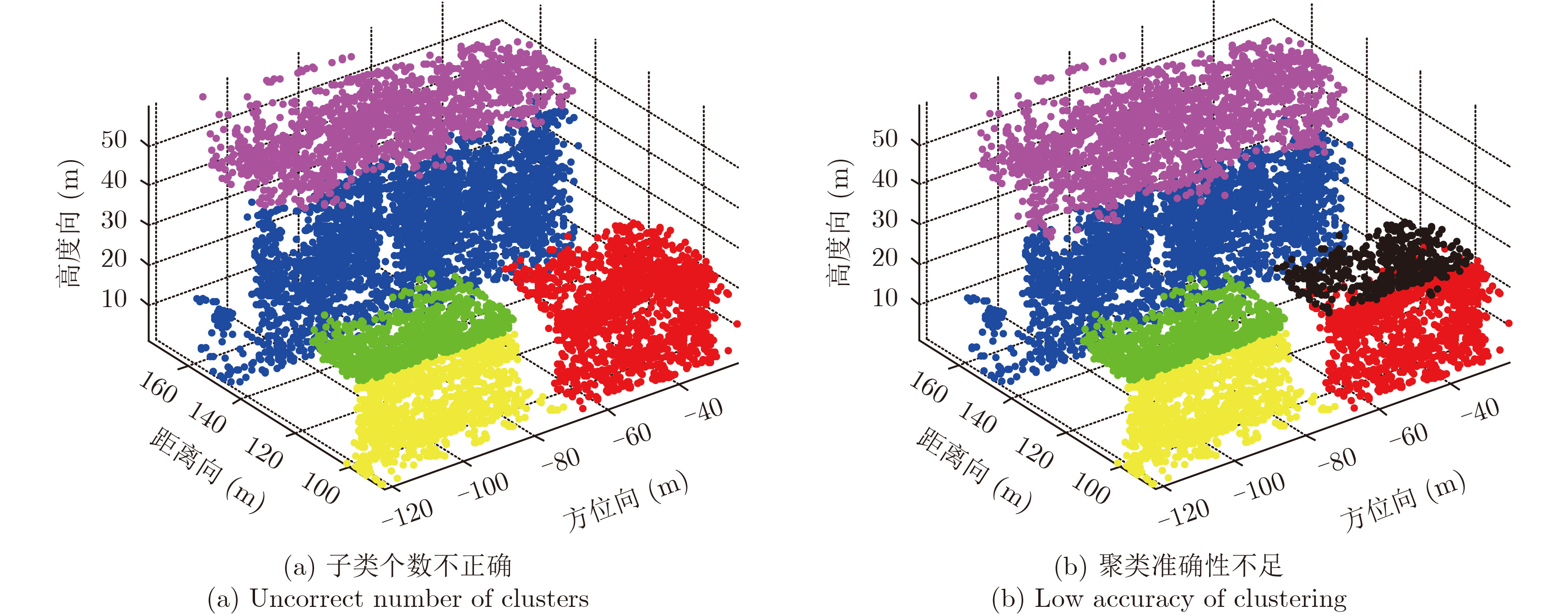
图10给出了K-means算法的聚类结果：图10(a)中，当聚类数目估计不正确时，会将楼顶点云较少的黑色楼顶点云聚类到红色小楼侧面点云中去；图10(b)中，当聚类数目设置准确，但由于K-means自身的性能和准确性导致的聚类结果不准确，将部分属于蓝色高楼侧面的点云聚类到了紫红色楼顶点云中去，红色小楼楼顶部分的黑色点云也被错误的聚类到了红色点云中去。这种聚类结果是具有随机性的，根据100次蒙特卡洛实验统计结果，使用本文的高斯混合聚类方法得到的聚类结果准确率达到95%左右，而K-means算法在聚类个数设定正确的情况下，聚类结果准确率只有62%左右。

4.3 建筑物3维成像结果

在上一步中获得了6个平面的SAR点云后，现在对每一个平面进行SAR图像反演。利用阵列干涉SAR系统参数对各个平面点云进行SAR图像反演，得到建筑物各个部分的SAR图像，同样再对原始点云中剔除掉建筑物散射点后剩下的属于地面的散射点进行SAR图像反演，得到整个地面的SAR图像，各个区域反演得到的SAR图像如图11所示。

图11显示了建筑物群各自平面的不叠掩的SAR图像，成功地从叠掩严重的原始2维SAR图像中解开了叠掩的区域，实现了叠掩场景中地面、楼梯侧面与楼顶的分离。由原始3维点云中提取出的地面区域点云SAR图像如图12所示。

利用检测到的建筑物轮廓和光学照片的先验信息，对所有反演得到的各个平面SAR图像进行地形融合和拼接，最终获取整个观测场景的3维成像结果。

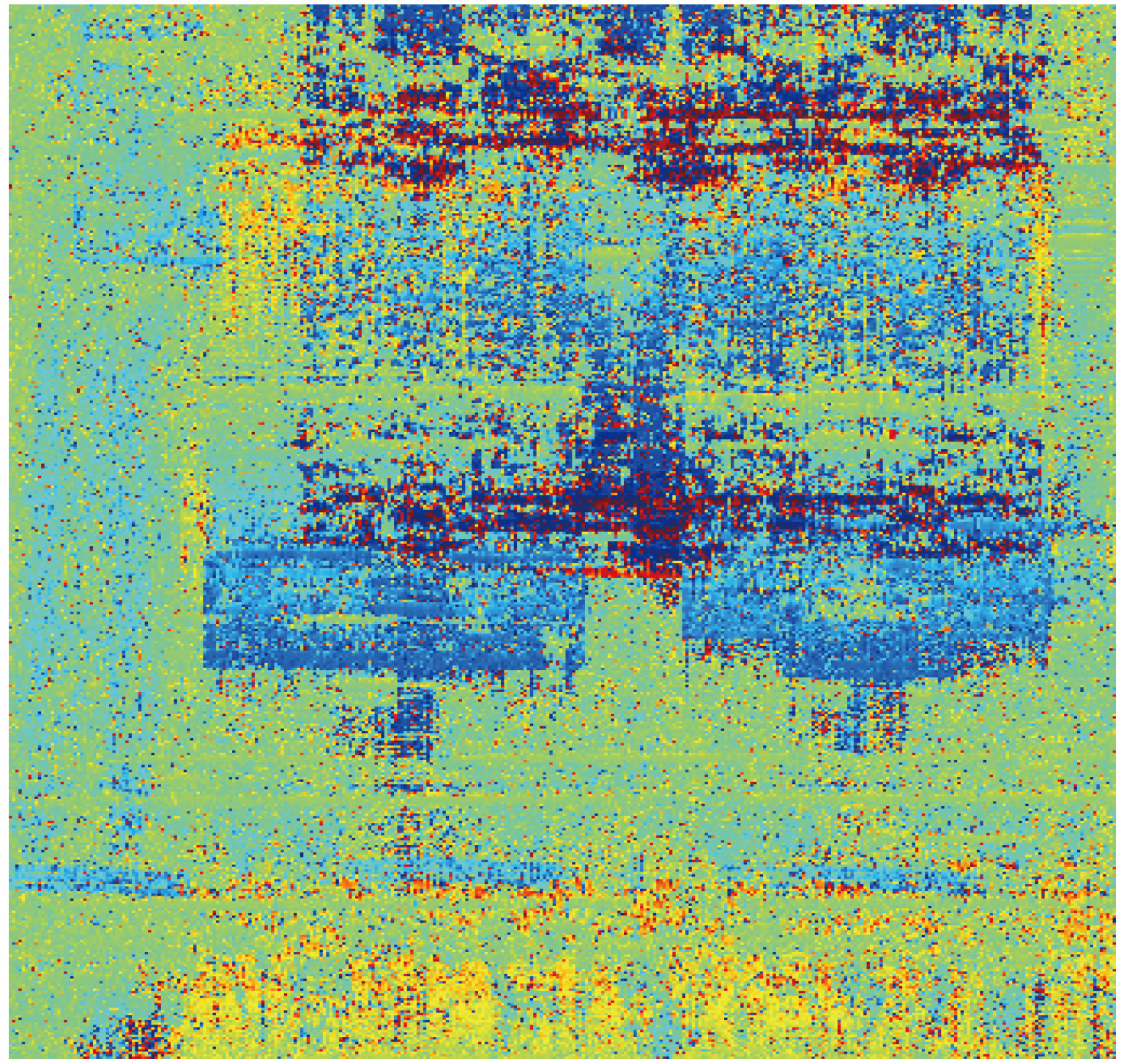
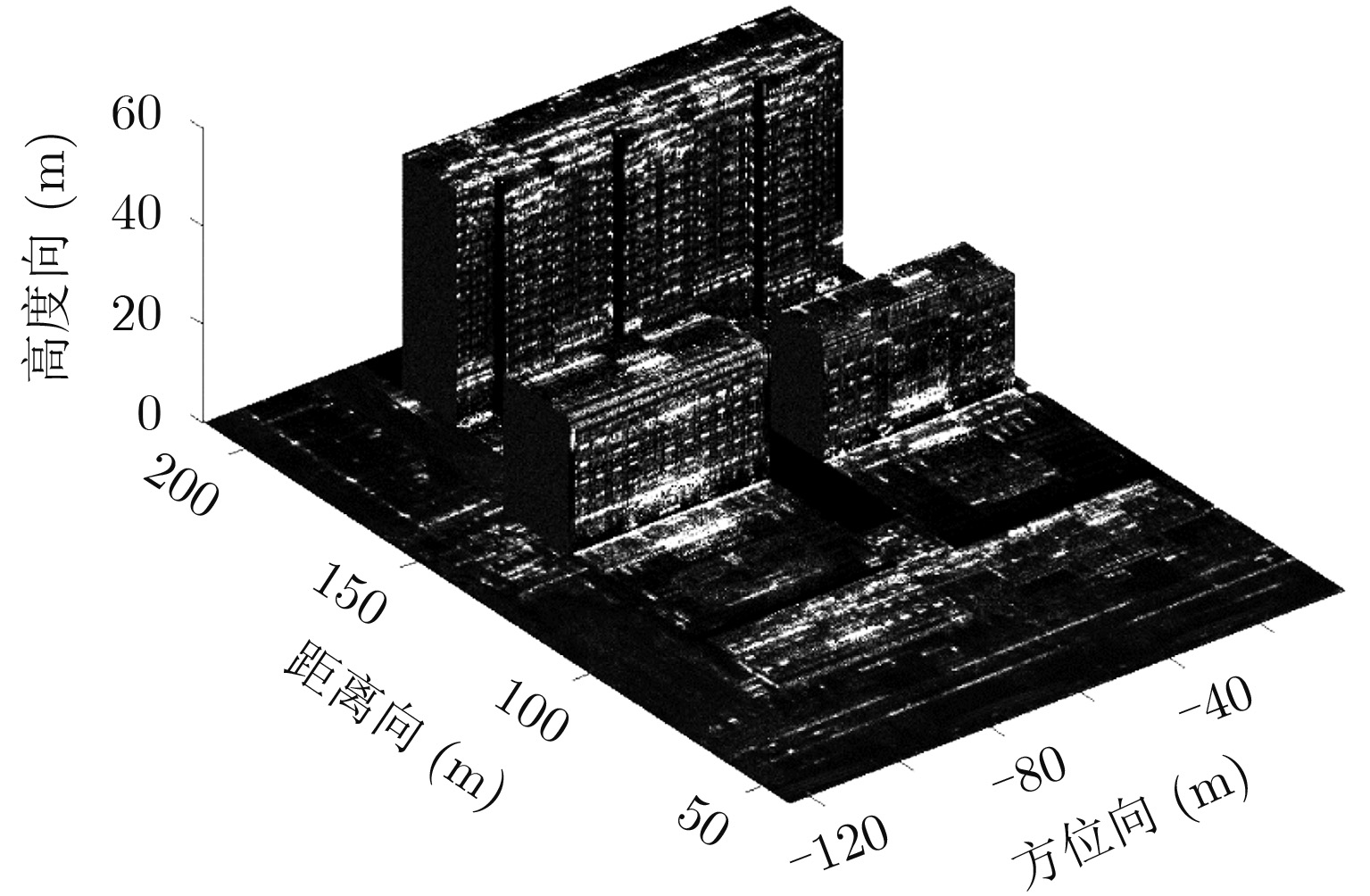
图13为观测场景的原始2维SAR图像，图14为该区域的干涉相位图。可以看出该区域的叠掩现象非常明显，通过肉眼无法区分不同建筑物以及同一建筑物的地面、楼侧和楼顶。图15为观测场景的最终3维成像结果，可以看到，不同建筑物被准确地区分开，肉眼即可非常清晰地观察到各幢楼体以及地面和楼顶的信息，重建得到小区高层建筑物的高度在52.6 m左右，前排小楼的高度在27.8 m左右，与实际高度相符。这是在国际上首次实现了基于机载阵列干涉SAR系统的城市建筑物群3维成像，从3维成像结果中可以提取丰富的楼群和地面信息，对城市建筑物的机载阵列干涉SAR 3维成像的发展和应用有着重要的意义。

5 结束语

本文论述了机载阵列干涉SAR 3维成像的基本原理，针对现有3维成像方法定位精度较差的问题，提出了一种基于高斯混合聚类的3维成像方法。该方法结合了阵列干涉SAR的高程分辨能力和高性能的聚类方法，充分利用阵列干涉SAR系统参数和场景先验信息，精确地完成了观测场景的3维重建。实际数据的处理结果表明，本文算法在城市区域的高分辨率SAR 3维成像中具有广阔的应用前景。后续研究中我们会进一步改进系统架构和算法性能，使其适合于处理更广区域、更复杂结构的城市场景3维测绘。