② (中国科学院电子学研究所 北京 100190)
② (Institute of Electronics,Chinese Academy of Sciences,Beijing 100190,China)
高分三号(GF-3)卫星是我国国家科技重大专项“高分辨率对地观测系列重大专项”的研制工程项目之一[1,2],具有高分辨率、大成像幅宽、多成像模式、长寿命运行等特点,能够全天候、全天时监测全球海洋和陆地信息,并通过左右姿态机动扩大对地观测范围、提升快速响应能力。该卫星可为我国国土资源监测、海洋权益维护、灾害天气预警等应用提供高质量高精度的稳定观测数据,对我国国民经济建设和促进国际区域合作具有重大意义。
高分三号卫星所搭载的C波段多极化合成孔径雷达,是迄今为止世界上成像模式最多的星载合成孔径雷达[3],该雷达具有全极化电磁波收发功能,并涵盖了诸如条带、聚束、扫描等12种成像模式。空间分辨率从1 m到500 m,幅宽从10 km到650 km。不仅能够用于大范围资源环境及生态普查,还能够清晰地分辨出陆地土地覆盖类型和海面目标,实现了既可探地,又可观海,达到“一星多用”的效果。此外,高分三号卫星还是我国首颗长寿命设计的低轨遥感卫星,在轨设计寿命8年,比我国以往遥感卫星3到5年的寿命长得多,与国际上遥感卫星6到7年的寿命相比,也处于领先地位。中国科学院电子学研究所承担了载荷总体研制和地面数据处理软件研制工作。
近年来,国际上星载SAR发展迅速,其图像产品的质量持续提升,如2006年发射升空的日本ALOS PALSAR, 2007年和2008年两年间发射的意大利COSMO-SkyMed系列SAR,加拿大的RadarSat-2系统以及德国的TerraSAR-X系统[4]。目前国外这些星载SAR系统的系统级几何定位精度可以达到10 m以内[5,6],尤其德国的TerraSAR-X标准产品,经过精细化的系统标定和处理,其定位精度甚至可以达到分米量级[7]。
本文结合GF-3卫星系统自身的特点,对GF-3卫星系统级几何定位误差源进行了全链路分析,并基于卫星在轨实际数据,对误差源进行了分析和校正,最后通过地面布设角反射器进行了系统级几何定位精度的实验验证,结果表明,通过误差标校和精细化处理后,高分三号卫星系统级几何定位精度可以达到3 m以内。
2 系统级几何定位的误差源分析如图1所示,系统级几何定位指在无地面控制点情况下,利用卫星测量数据、雷达参数以及成像处理参数,基于斜距多普勒方程组联立求解获得图像的地理经纬度[8]。根据斜距多普勒模型,影响系统级几何定位的因素主要有天线相位中心位置速度误差、SAR系统时间误差、大气传播延迟误差、成像处理引入误差以及地面相对高程误差。
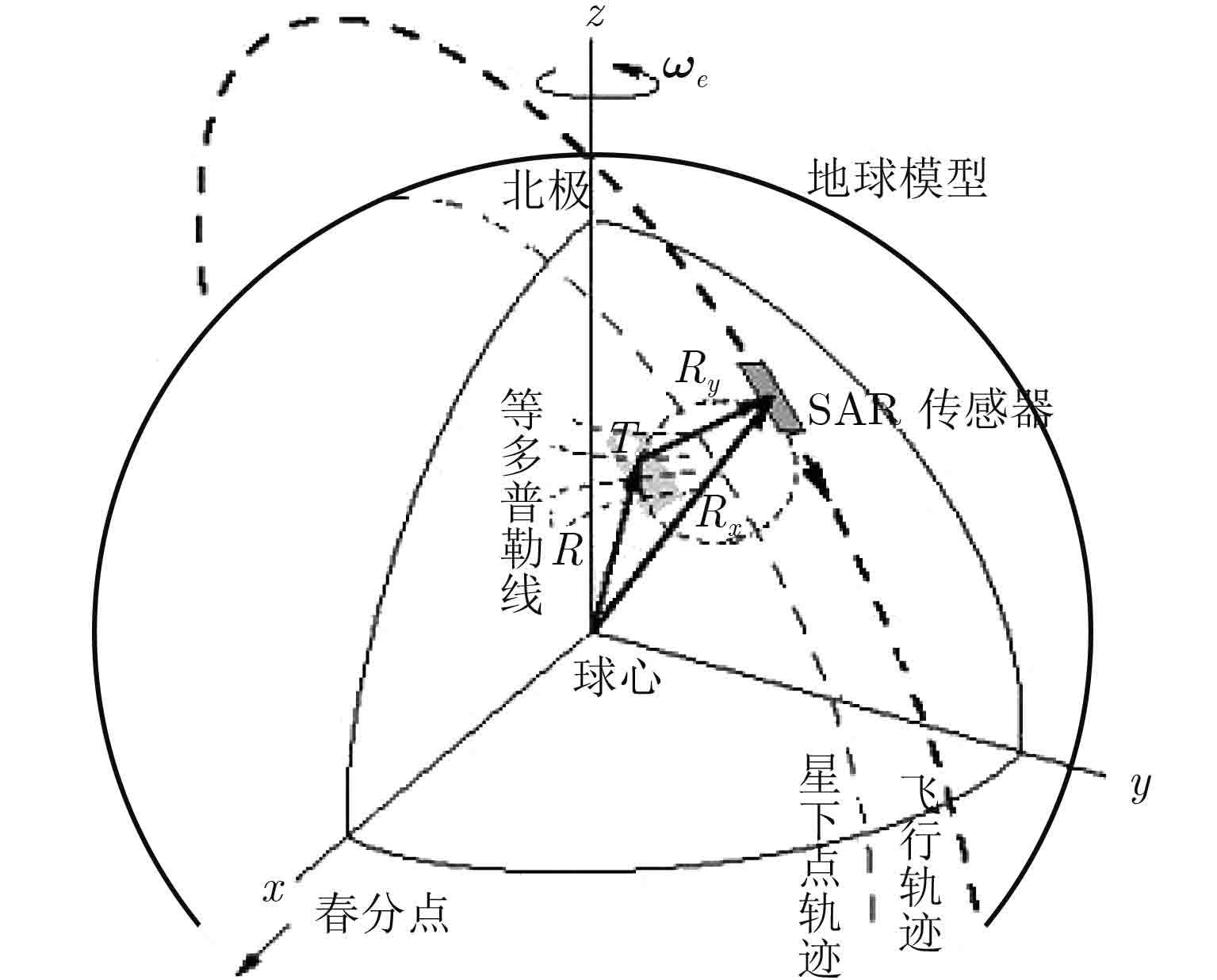
|
图 1 星载SAR斜距多普勒定位模型 Fig.1 The range-Doppler model of spaceborne SAR |
天线相位中心位置、速度误差主要由卫星测量误差和天线相位中心转换误差导致。
2.1.1 卫星测量误差 卫星位置测量误差主要指与SAR成像时间相比具有缓变特性的误差,分为沿航向位置误差、径向位置误差和垂直航向位置误差。沿航向的轨道位置误差引起图像方位向定位误差,其定位误差与航迹向的轨道位置误差大小几乎相等;垂直航向的轨道位置误差主要引入距离向定位误差,其定位误差略小于轨道位置误差,且基本不随入射角而变化。沿雷达到目标径向的轨道位置误差主要引入距离向定位误差,距离向定位误差约等于径向的轨道位置误差除以目标处入射角的正弦,即入射角越小,定位误差越大。
速度测量误差主要体现的是SAR成像时间内的短期轨道误差,其将引起目标多普勒计算误差,从而引起成像位置偏差(如时域BP算法)或多普勒方程构建误差(如频域算法),进而引起定位误差。
目前高分三号卫星采用了双频GPS进行测轨,通过事后精密轨道处理后,其位置精度可以达到5 cm,速度精度为0.05 mm/s。图2和图3分别给出了采用双频GPS确定的GF-3卫星精密轨道每天6 h重叠轨道之间的位置矢量和速度矢量的绝对值差异。
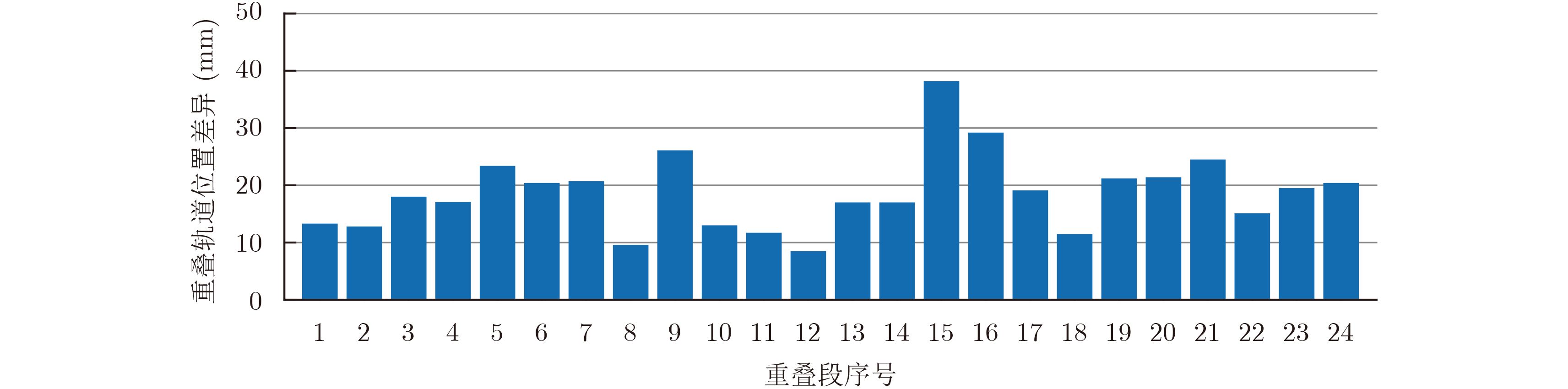
|
图 2 精密轨道每天6 h重叠位置差异图 Fig.2 The overlap position difference map of six hours per day of precise orbit |
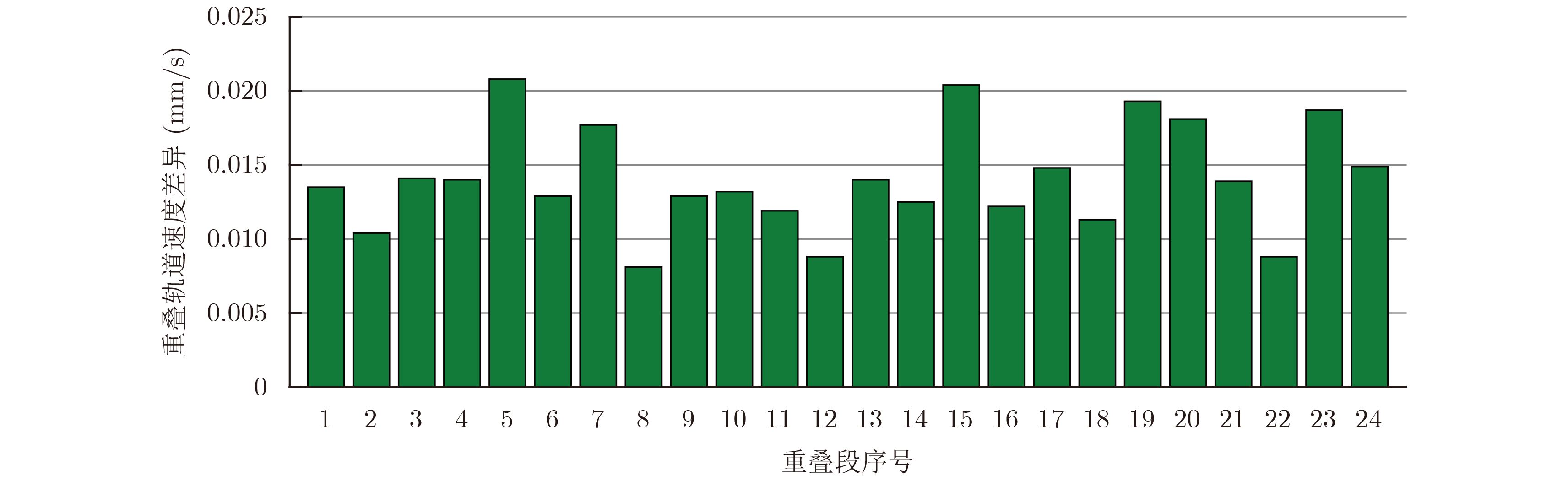
|
图 3 精密轨道每天6 h重叠速度差异图 Fig.3 The overlap velocity difference map of six hours per day of precise orbit |
2.1.2 天线相位中心转换误差 由于轨道位置测量的传感器并不能装在天线相位中心位置,故其实际测得的轨道位置并非天线相位中心的位置。然而,SAR定位需要采用的实际上是天线相位中心的位置参数,因此,轨道位置测量值还需转换为天线相位中心测量值,并且随着卫星姿态的变化,转换关系也需进行相应的调整,否则也会引入图像几何校正误差。
高分三号卫星天线相位中心与GPS测定位置中心之间约2 m的距离,处理时利用星体坐标系下两者坐标位置关系进行了坐标转换,其残余转换误差仅为分米量级。
2.2 SAR系统时间误差SAR系统时间误差包括采样延迟误差,方位时间误差以及由晶振稳定性引起的采样率误差、脉冲重复频率误差。
2.2.1 系统时延误差 系统时延误差会导致SAR测算的斜距存在误差,从而导致距离向定位误差及距离向图像内部畸变。另外,系统时延误差会带来对每个回波脉冲接收起始时刻的时间戳记录存在误差,使脉冲时间与其所对应的轨道信息时间之间存在时间差,从而导致计算得到轨道信息存在沿轨位置误差,进而影响图像定位精度。
高分三号卫星设计了延迟标定回路,可获得相应的内定标数据。地面处理时首先对获取的内定标数据分别提取全阵面收发通路、标定通路、参考通路的信号,然后对相应定标通路进行脉冲压缩,并分析脉冲压缩后峰值相对零时刻的时间得到相应的通路时延,最后结合卫星给出的固定时延,计算出不同时带宽下的系统时延。
图4给出对高分三号20 MHz带宽&45 μs脉宽下,对8次不同时间的内定标数据进行分析,其结果表明系统时延一致性很好,变化仅在2 ns以内,也即体现至斜距上仅有0.3 m以内的变化。
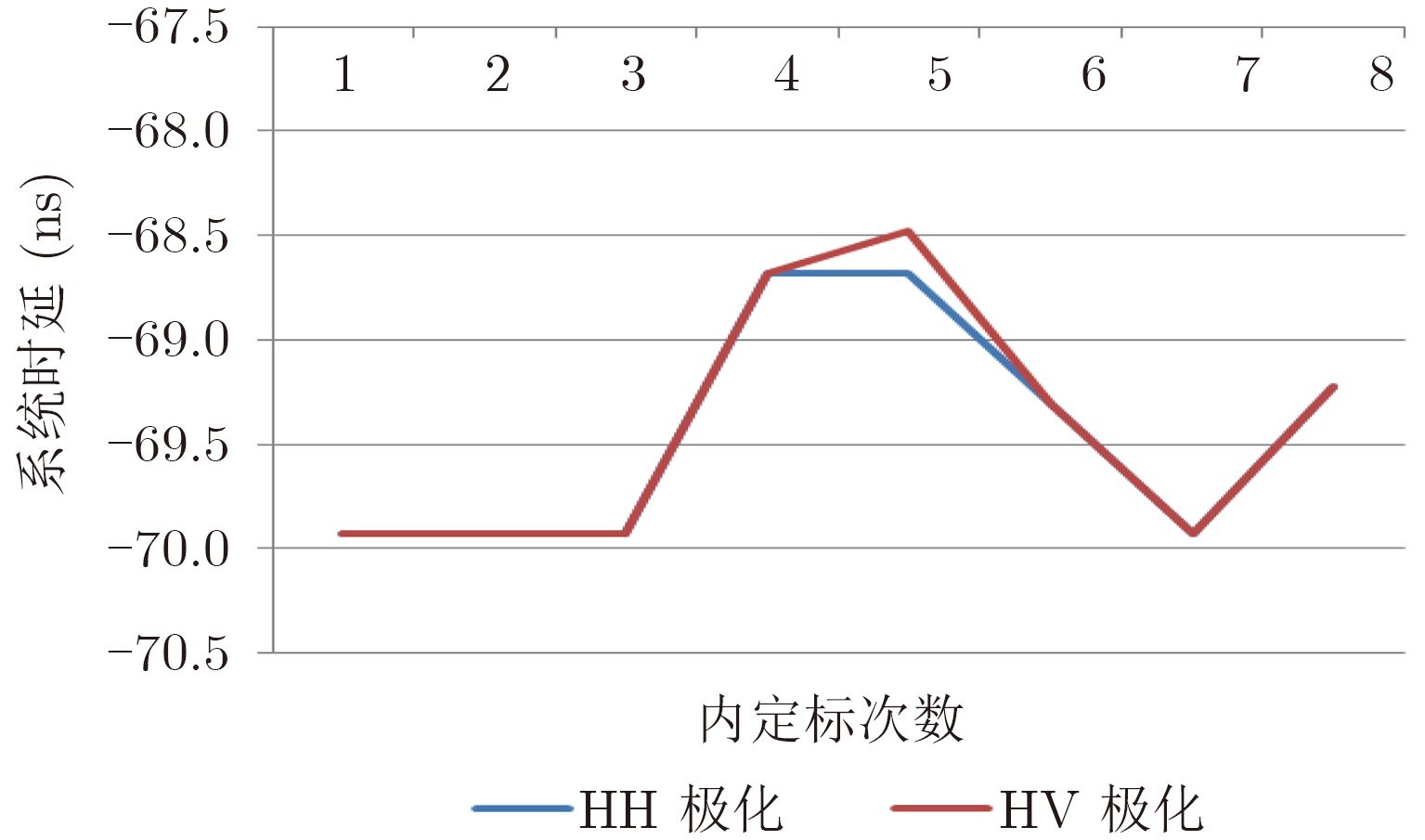
|
图 4 20 MHz带宽&45 μs脉宽下内定标的系统时延标定值 Fig.4 The system time delay value of internal calibration with 20 MHz bandwidth and 45 μs pulse width |
2.2.2 方位时间误差 一般星上时钟更新频率2 Hz,与SAR的脉冲频率不能匹配,存在方位时间整体的偏移,进而导致图像定位偏差。高分三号卫星设计了秒脉冲时间机制,通过对每条脉冲进行计数获得准确的方位时刻,其精度可以达到30 ns,由此带来的方位误差约为0.2 mm,可以忽略。
2.2.3 采样率误差 采样率误差由系统晶振标称值误差和晶振稳定度引起,其导致成像及定位处理采用的采样率与系统真实采样率之间存在偏差,引起图像畸变。目前高分三号卫星的晶振短期稳定度为10–11,长期稳定度为10–7。对于高分三号卫星滑动聚束模式下240 MHz带宽,引起图像斜距变化约0.001 m。
2.2.4 脉冲重复频率误差 脉冲重复频率的误差同样由基础晶振误差引起,通过分频器获得。由于高分三号卫星的晶振稳定度很高,引起的脉冲重复频率的变化很小,可以忽略不计。
2.3 大气传输延迟误差微波在大气中的传播延迟误差将影响SAR的斜距计算精度,从而影响到图像的定位精度,并引起图像畸变。大气传播影响主要包括电离层的影响和对流层的影响[9]。电离层是从60~2000 km高空的区域,其浓度从60 km向上逐渐增加,至300~400 km达到最大,后又随高度增加逐渐减小,是一种色散介质。对流层平均离地12 km,对频率20 GHz以下的电磁波为非色散介质。
电离层由于群延迟效应造成斜距误差,对于C波段的高分三号卫星来说,以20TECU为例,斜距偏差约为0.27 m。对流层延迟主要依赖高度,还与气压、温度和水汽等因素有关。对于海平面,高分三号视角范围内的对流层延迟在2.4~3.6 m之间。一般在产品生产时可利用只与高度相关的简化静态模型[10],或者包含了气压、温度和水汽的静态湿温压模型对大气进行修正[11]。如有实测气象数据,则可对获取的实测气象数据插值出不同高度的气象值,进而得到每一层的折射率剖面,延迟由每层沿SAR信号传播路径对大气的折射率进行积分,从而利用更加精确的RT模型[7]进行校正。本文中,由于并未采集同步观测的气象数据,采用了简化静态模型进行了大气校正,由此带来的斜距误差约在1 m以内。
2.4 成像处理引入误差成像处理是通过多普勒频域算法将SAR原始回波信号聚焦为斜距图像。只要斜距多普勒模型中采用成像处理过程中的多普勒中心频率,则基本不会引入定位误差[12]。以往成像处理和几何定位均基于“停-走”模型,该模型认为SAR在发射和接收同一个脉冲期间是不动的,由此忽略卫星发射、接收脉冲期间,以及接收脉冲持续时间段内的卫星运动,从而带来随距离向变化的方位向定位误差。本文在处理高分三号卫星数据时,采用了与卫星实际运动相符的“持续运动”模型[13],从而避免了这一误差的产生。
2.5 相对高程误差由于SAR是侧视成像,并且只能测量距离和多普勒两维信息,要实现准确的定位必须依赖于外源高程数据的支撑。高程误差引入的定位误差约等于
高分三号SAR卫星于2016年8月成功发射,并开展了为期5个月的在轨测试任务。中国科学院电子学研究所在三河市平坦地区放置了两个角反射器,并利用天宝R5进行了精确的地理位置的测量,如图5。由于天宝R5无法准确布设到角反射器的反射中心,所以测量的地理位置与实际SAR图像上的位置相差约1 m,该项也影响了高分三号卫星系统级几何定位精度的测试。图6(a)是角反射器布设位置的地图,图6(b)是在滑动聚束模式图像上的角反射器。

|
图 5 角反射器及天宝R5 Fig.5 The corner reflector and Timbel R5 |

|
图 6 角反射器的位置示意图 Fig.6 The place of corner reflectors |
首先,我们使用事后精密轨道数据对角反射器进行几何定位,其中RD模型中的高程是由天宝R5精确测量的角反射器高程数值。然后将定位结果与天宝R5精确测量的地理经纬度分别转换到地图坐标系统下进行比较。表1给出了不同入射角下高分三号卫星的定位精度,其4组定位精度的RMS为2.56 m。图7分别给出了2016年10月拍摄的高分三号卫星滑动聚束模式下的斜距图像和对应的几何校正后的图像。
| 表 1 角反射器的定位精度 Tab.1 The positioning accuracy of the corner reflectors |

|
图 7 高分三号卫星聚束模式下图像 Fig.7 The images of sliding spotlight mode of GF-3 satellite |
本文通过对高分三号卫星系统级几何定位精度的影响因素进行了全面分析,并进行了精细化的处理,包括:(1)对双频GPS进行事后处理获取厘米量级的精密轨道;(2)结合卫星给出的固定时延,对内定标数据进行脉冲压缩计算真实的系统延迟;(3)对大气延迟进行修正;(4)基于卫星真实的“持续运动”模型进行成像和几何校正,从而获得了较高定位精度。经过角反射器的实验,结果表明高分三号卫星的定位精度可以达到3 m。
后续随着高分三号在轨运行,将监测SAR卫星系统时延变化等情况,采用更精确的大气修正模型,并修正角反射器测量带来的误差,进而保证SAR卫星产品的几何定位精度。
致谢: 感谢武汉大学卫星导航定位技术研究中心提供的高分三号卫星事后精密轨道位置速度差异图。| [1] |
Guo Huadong. China’s Earth Observation Development[C]. The 36th International Symposium on Remote Sensing of Environment (ISRSE36), Berlin, 2015.
( 0) 0)
|
| [2] |
庞丹, 潘晨, 紫晓. 高分三号: 辽阔疆域的" 守望者”—写在高分三号卫星发射成功之时[J]. 中国航天, 2016(9): 8–12.
Pang Dan, Pan Chen, and Zi Xiao. GF-3: The watcher of the vast territory[J].Aerospace China, 2016(9): 8–12. http://mall.cnki.net/magazine/Article/ZGHT201609003.htm (  0) 0)
|
| [3] |
云菲. 高分三号卫星[J]. 卫星应用, 2016, 第8期.
Yun Fei. GF-3 Satellite[J].Satellite Application, 2016, No.8. http://d.wanfangdata.com.cn/Periodical/wxyy201608021 (  0) 0)
|
| [4] |
尤红建, 付琨. 合成孔径雷达图像精准处理[M]. 北京: 科学出版社, 2011: 13.
You Hong-jian and Fu Kun. Image Precise Processing of Synthetic Aperture Radar[M]. Beijing: Science Press, 2011: 13. (  0) 0)
|
| [5] |
Schubert A, Small D,et al.. COSMO-skymed, Terra SAR-X, and RADARSAT-2 geolocation accuracy after compensation for earth-system effects[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS2012), Germany, 2012: 3301–3304.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6350598 ( 0) 0)
|
| [6] |
Dan Williams, Pierre LeDantec,et al.. RADARSAT-2 image quality and calibration update[C]. Proceedings of the 10th European Conference on Synthetic Aperture Radar, EUSAR 2014, Denmark, 2014: 1–4.
http://ieeexplore.ieee.org/document/6856981/ ( 0) 0)
|
| [7] |
Eineder M, Minet C,et al.. Imaging geodesy—Toward centimeter-level ranging accuracy with TerraSAR-X[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 667–671.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5570983 ( 0) 0)
|
| [8] |
Curlander J C and McDonough R N. Synthetic Aperture Radar: Systems and Signal Processing[M]. New York: John Wiley & Sons, Inc, 1991: 374–377.
http://www.oalib.com/references/9206174 ( 0) 0)
|
| [9] |
Doerry A W. Atmospheric loss considerations for synthetic aperture radar design and operation[C]. Proceedings SPIE 5410, Radar Sensor Technology VIII and Passive Millimeter-wave Imaging Technology VII, 2004. DOI: 10.1117/12.542327.
https://www.researchgate.net/publication/241390270_Atmospheric_loss_considerations_for_synthetic_aperture_radar_design_and_operation ( 0) 0)
|
| [10] |
Fritz T, Eineder M,et al.. TerraSAR-X Ground Segment Basic Product Specification Document. Feb.24, 2008. TX-GS-DD-3302 Iss.1.5.
( 0) 0)
|
| [11] |
Michael Jehle, Donat Perler, David Small,et al.. Estimation of atmospheric path delays in TerraSAR-X data using models vs. measurements[J].Sensors, 2008, 8(12): 8479–8491.
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3791028/ ( 0) 0)
|
| [12] |
刘佳音, 韩冰, 仇晓兰. 基于等效距离模型的改进RD定位算法[C]. 第一届高分辨率对地观测学术年会, 北京, 2012.
Liu Jiayin, Han Bing, and Qiu Xiaolan. Improved RD Location Algorithm based on equivalent range model[C]. The 1st China High Resolution Earth Observation Conference, Beijing, 2012. (  0) 0)
|
| [13] |
仇晓兰, 韩传钊, 刘佳音. 一种基于持续运动模型的星载SAR几何校正方法[J].
雷达学报, 2013, 2(1): 54-59. Qiu Xiao-lan, Han Chuan-zhao and Liu Jia-yin A Method for Spaceborne SAR Geolocation Based on Continuously Moving Geometry [J] A Method for Spaceborne SAR Geolocation Based on Continuously Moving Geometry[J]. Journal of Radars, 2013, 2(1): 54-59. DOI:10.3724/SP.J.1300.2013.20072 (  0) 0)
|




