② (中国科学院大学 北京 100049)
② (University of Chinese Academy of Sciences, Beijing 100049, China)
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种微波遥感设备,在遥感领域具有举足轻重的地位。由于其具备优良的全天时、全天候、宽测绘带、远程成像等能力,已被广泛应用于军事和民用等诸多领域,如地质勘探、地形测绘、灾害评估、海洋应用、军事侦察、农林检测[1,2]。频率越低,信号覆盖和渗透性能越好,越有利于环境资源的检测,以及军事监视。然而,低频段内同时存在移动通信信号、电视信号、广播信号等其它信号[3],它们会对SAR信号产生干扰,即所谓的射频干扰(Radio Frequency Interference, RFI)。在SAR图像中,RFI通常沿距离向以密集的雨滴或明亮的条纹的形式出现,会对有用信号产生许多不良影响,如降低信干噪比(Signal to Interference plus Noise Ratio, SINR),淹没潜在的感兴趣目标,严重降低SAR成像质量,在高分辨率情况下该影响尤其严重。因此,射频干扰检测和抑制对SAR图像应用具有重要的意义。
到目前为止,国内外学者已经提出了众多方法来抑制RFI,这些方法通常可以分为两类:参数化方法和非参数化方法。参数化方法,通常是基于将RFI看作是一系列正弦信号叠加的假设,通过特定的数学方法[4,5]来估计正弦干扰信号的振幅、频率和相位,然后从混有干扰的回波信号中减去估计出的正弦信号,进而实现干扰抑制。该类方法包括最小均方法(Least Mean Square, LMS)[6,7],最大似然估计法[8]等。在最优的情况下,利用参数化方法,可以准确估计出RFI信号模型参数,实现其与假设模型参数的完全匹配。然而,在实际情况下,射频干扰的数学模型相当复杂,或多或少会出现模型失配,产生模型参数估计误差,进而导致RFI估计不准确。此外,参数化方法需要额外的参数估计过程,大大降低了信号处理效率。其中,LMS自适应滤波法是一种典型的参数化方法,通过使干扰信号的方向上能量最小化来减少RFI。但是,该方法不能满足SAR实时成像的要求,同时可能会导致大量有用信号的损失。非参数方法,可以在没有任何先验知识或参数模型的情况下实现RFI抑制。多数非参数化方法都可以利用原始数据自适应地实现RFI抑制,其中最简单最典型的方法就是陷波法[9]。陷波法首先检测包含干扰的信号频谱,辨别出RFI信号的尖峰脉冲,然后通过频谱置零的方式来实现RFI抑制。陷波法可以简单快速地实现RFI抑制,但是也会给SAR成像结果带来不利影响,例如信号频谱的不连续,距离向分辨率的降低,信噪比(Signal-to-Noise Ratio, SNR)的损失,等等。子空间滤波法将RFI投影到干扰子空间[10],然后从原始信号中去除投影部分,进而实现RFI抑制。然而,该方法对整块数据进行处理,会损失部分有用信号。一些非参数方法可以基于成像后的复数据来实现,子带谱对消(Subband Spectral Cancelation, SSC)法是其中典型的一种[11]。SSC法不需要进行干扰检测和估计,通过SAR图像不同距离子带频谱对消来实现RFI抑制。但是如果频谱不具有对称性,就会导致有用信号的大量损失。
本文提出了一种应用于SAR图像的改进的特征子空间射频干扰抑制算法。首先,进行初步的RFI检测,判断数据中是否存在干扰。若存在干扰,则进行后续的RFI检测,在频域和时域分别判断干扰所在的区域。最后,在前两步的基础上,利用传统的特征子空间法来去除原始数据中的干扰信号。仿真和实测实验的处理结果表明,本文所提出的方法处理效率更高,效果更好。
本文将围绕改进的特征子空间法展开论述。第2节介绍了射频干扰的特点。第3节详细介绍了我们提出的方法。第4节给出了实验结果和相应的分析。最后,第5节给出本文的结论。
2 RFI的特性在SAR系统中,包含噪声和RFI的目标信号可用如下的数学模型表示

|
其中S表示有用信号,I代表RFI信号[12,13],N代表噪声信号。
由于有用信号和噪声信号均可视为白噪声信号,因此可以直接将上述公式表示为
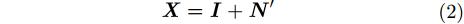
|
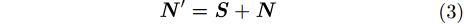
|
图1为原始数据(机载L波段SAR系统)的距离向频谱,其中图1(a)为完整频谱图,图1(b)和图1(c)分别为图1(a)中的红框(b)和红框(c)内的部分的放大。沿距离向的亮条纹即为RFI,这些RFI各不相同,有的在带内,有的在带外,有的具有周期性,有的仅出现在某些回波内。然而,它们有一个共同特征——窄带性。

|
图 1 由工作在L波段的机载SAR系统获得实测数据的距离频域方位时域幅度图 Fig.1 The range direction spectrum of the measured data obtained by an airborne SAR system working at L-band |
对实测数据进行分析,可以看出回波信号的时域波形受到窄带射频干扰的严重影响。一方面,由于SAR天线与射频干扰源的相对位置的变化和脉冲重复时间的差异,很难确定窄带射频干扰的绝对功率。另一方面,对多个目标回波的叠加导致回波的波形在时域上是无序的,因此很难仅靠观察时域波形来判断是否存在干扰[14]。
事实上,由于射频信号的窄带特性,其能量高度集中在频率域,所以我们可以利用该特点进行频域检测,这样可使干扰的识别和判断更容易。
图2是由图1中的数据沿方位向叠加而得到的。通过对实测数据的统计分析可知,SAR数据中窄带RFI的带宽分布在0.1 MHz到10 MHz的范围内,这要比SAR系统的带宽小得多。与射频干扰的带宽相比,可以认为SAR系统的工作带宽比前者大得多,所以通常在后续处理中将射频干扰视为窄带干扰信号。

|
图 2 距离向频谱图 Fig.2 Average range direction spectrum of Fig. 1 |
在该L波段机载SAR实测数据中,主要干扰所在频段为1335–1345 MHz,产生原因可能为航空无线电导航、无线电定位、卫星无线电导航(地对空)。周期干扰所在频段为1377–1390 MHz,产生原因应该为无线电定位。
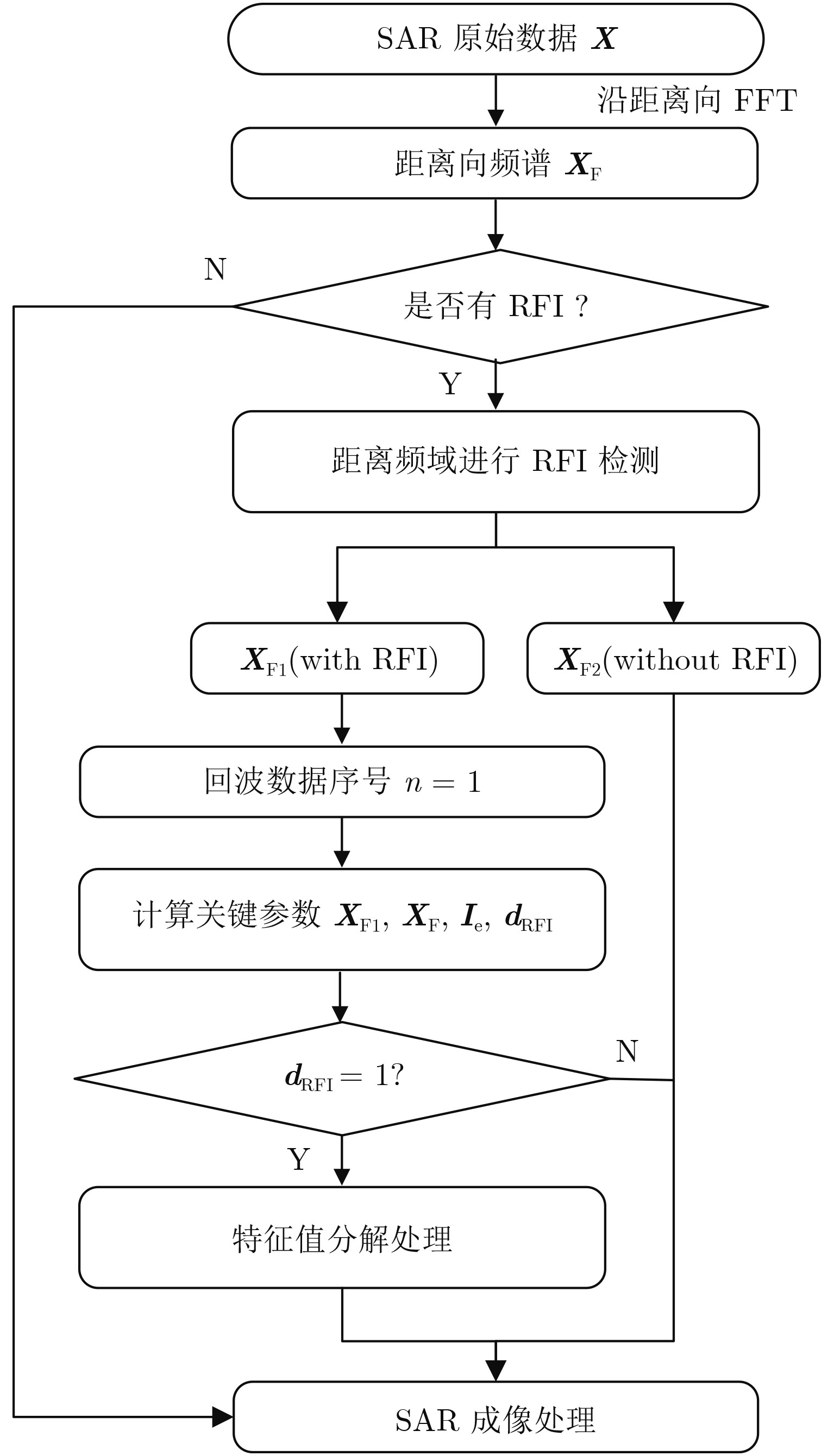
3 算法介绍为了实现干扰抑制,首先需要检测和识别RFI信号。传统的特征子空间法只是在原始数据的频域进行粗略检测,以确定RFI在该数据中是否存在,之后对存在RFI的数据进行后续处理。而事实上,干扰在频域具有窄带特性,在时域也具有区域局部性,对整块数据进行特征值分解处理会带来有用信号的损失。同时,特征值分解处理非常耗时,对整块数据进行处理效率很低。本文提出了改进的特征子空间法,主要分为3部分:初步RFI检测,分别在距离频域和方位时域进行特定的RFI检测,RFI抑制。其中,初步RFI检测是对整块数据中是否存在干扰进行检测,在存在干扰的情况下进行后续处理;距离频域RFI检测利用了支持向量回归(Support Vector Regression, SVR)算法,得到干扰所在的距离频域范围;方位时域RFI检测则是通过向量RFI_detect得到干扰所在的方位时域范围;最后,只对存在干扰的数据区域进行特征值分解处理,将得到的处理结果与不含干扰的数据部分合并,进行后续成像。该方法的主要步骤流程图如图3所示。该方法的细节部分将在后面继续讨论。应该注意的是,在本文中,SAR图像的横向代表方位向,纵向代表距离向,即一行代表一个距离门,一列代表一条距离线。
|
图 3 改进的特征子空间法的主要步骤流程图 Fig.3 Main flowchart of main steps of proposed approach |
为了避免无意义的RFI抑制处理,需要进行初步RFI检测,判断数据中是否存在RFI。首先,对原始数据X沿距离向进行快速傅里叶变换(Fast Fourier Transform, FFT),得到原始距离频域方位时域数据XF。然后,计算XF每一行(沿方位向)幅度值的平均值,得到一个列向量XF_Mean,如下:

|
其中,k代表距离门序号,K代表距离门总数,XF由原始数据X经距离向FFT得到。可以从XF_Mean中获取距离频域信息。通过对比XF_Mean中各个元素的幅度值,可以很容易地实现初步RFI检测。
3.2 分别在距离频域和方位时域进行特定RFI检测在进行初步RFI检测之后,并且确定该原始距离频域方位时域数据XF存在干扰的情况下,需要分别在距离频域和方位时域进行特定RFI检测。
3.2.1 距离频域RFI检测首先需要进行特定的距离频域RFI检测,即需要检测干扰所在的距离向频谱范围。可以利用多种方法来进行频域RFI检测,例如SVR等方法[15,16]。下面简单介绍一下SVR方法。
假设给定训练数据
首先对线性函数f的条件进行描述,该函数具有以下形式:
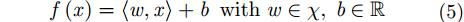
|
其中,
我们可以将该问题转化为凸优化问题:
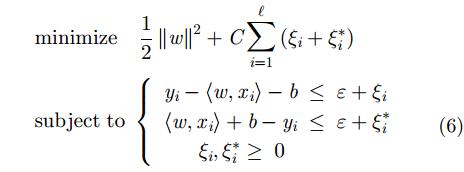
|
其中常数
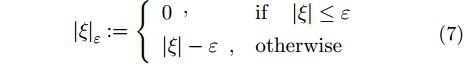
|
我们可以利用核函数将SVR应用于非线性的情况下。常用的核函数包括多项式核、高斯核(Radial Basis Function, RBF)、拉普拉斯核、Sigmoid核等[17]。
在这里,我们选择高斯核进行处理。输入数据为图2的结果(向量数据),利用采用高斯核的SVR算法处理,得到RBF模型(也是向量数据)。图2的结果与得到的RBF模型相减,可以得到拟合误差,公式如下:
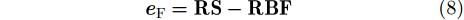
|
其中,eF代表拟合误差,RS代表图2的结果(向量数据),RBF代表得到的RBF模型(向量数据)。
为拟合误差eF设定阈值,高于阈值的判断为干扰部分,即可判断出RFI所在的距离向频谱范围。
在确定出干扰所在的频谱范围之后,可以将数据XF直接在距离频域方位时域空间上划分为两部分,XF1和XF2。其中,XF1包含干扰,XF2不含干扰。
3.2.2 方位时域RFI检测此外,还需要特定的时域RFI检测(针对包含干扰的数据XF1)。可以依次检测XF1中每条回波数据中是否存在干扰,以便进行后续RFI抑制处理。具体来说,对数据XF1沿距离向求幅度平均值,得到行向量dL;对数据XF沿距离向求幅度平均值,得到行向量dT。可以定义参数向量Ie如下:
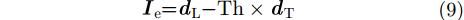
|
其中Ie代表判断每条回波数据是否存在干扰的参数向量,dL代表对数据XF1沿距离向求幅度平均值而得到的行向量,dT代表对数据XF沿距离向求幅度平均值而得到的行向量,Th代表设定的的阈值。
之后,可以得到向量dRFI

|
其中,dRFI用于表示每条回波数据中是否存在RFI, Ie代表判断每条回波数据是否存在RFI, sign代表用于判断参数符号的符号函数(相关参数大于0时,结果为1;相关参数等于0时,结果为0;相关参数小于0时,结果为–1)。
然后,综合频域和时域检测的结果,可以确定出干扰在数据XF1中存在的范围,得到距离频域方位时域数据XF1t和XF2t,其中XF1t包含干扰,XF2t不含干扰。分别对XF1t与XF2t沿距离向进行IFFT,得到2维时域数据X1t与X2t(由于IFFT为线性变换,X1t与X2t之和为原始2维时域数据X),其中X1t包含干扰,X2t不含干扰。
3.3 RFI抑制在经过上述处理之后,我们成功完成了RFI检测,然后利用传统的特征子空间法[18]对包含干扰的2维时域数据X1t进行后续的RFI抑制处理。
整个处理流程包括数据分块,相关矩阵估计,特征值分解,干扰子空间构建,数据投影和数据重排。
假设xm代表第m个距离向采样点(
首先,将包含干扰的2维时域数据X1t分成K个L维子向量,其中
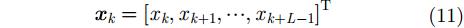
|
然后,可以构建一个

|
我们可以利用前面的公式来得到干扰的估计协方差相关矩阵,如下:

|
之后,对矩阵
如果下面的不等式成立:

|
其中

|
在将

|
从原始数据之中去除掉求得的干扰数据,即可得到不含干扰的数据,有如下形式:

|
之后,我们可以构建一个新的不含干扰的数据矩阵:
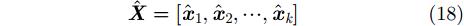
|
然后,对数据矩阵
(1) 距离频域检测部分:
(a) 距离频域RFI检测(即SVR)的输入数据为图2的结果(向量数据),利用采用高斯核的SVR算法处理,得到RBF模型(也是向量数据)。
(b) 拟合误差
(c) 在确定出干扰所在的频谱范围之后,可以将数据XF直接在距离频域方位时域空间上划分为两部分,XF1和XF2。其中,XF1包含干扰,XF2不含干扰。
(2) 方位时域检测部分:
(a)对XF1进行方位时域检测,进一步缩小包含干扰的数据范围,得到包含干扰的部分XF1t,以及不包含干扰的部分XF2t(XF1t与XF2t之和为XF)。
(b) 分别对XF1t与XF2t沿距离向进行IFFT,得到2维时域数据X1t与X2t(由于IFFT为线性变换,X1t与X2t之和为原始2维时域数据X)。
(3) RFI抑制部分:
(a) 对包含干扰的2维时域数据X1t进行第3.3节的RFI抑制(即利用传统特征子空间法处理),得到2维时域数据X1ts。
(b) 最后,将X1ts与X2t重新组成数据矩阵X ′ ,进行后续正常的成像。
(4) 需要特别说明的是:
(1) FFT和IFFT均为线性变换,先求和后变换与先变换后求和对处理结果没有影响。
(2)XF, XF1, XF2, XF1t与XF2t均为距离频域方位时域数据,X, X1t, X2t, X1ts与X ′ 均为2维时域数据。
4 实验结果与分析在该节中,分别利用仿真实验和机载SAR实测数据进行验证,实验结果证明了本文所提算法在SAR图像干扰抑制中的有效性。
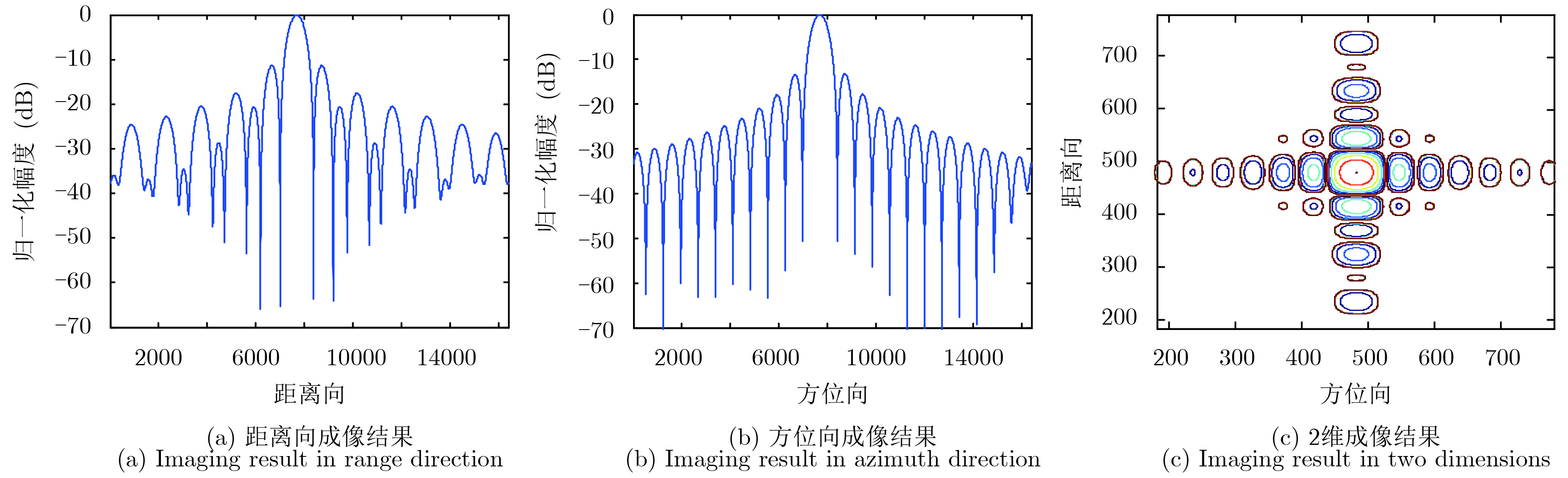
4.1 仿真实验为了初步证明提出的改进方法的有效性,首先进行了仿真实验。仿真实验的主要系统参数如表1所示。在该仿真实验中,添加了干信比为40 dB的单频干扰,然后分别利用传统的特征子空间法和改进的特征子空间法进行处理。传统方法和改进方法的处理结果分别如图4和图5所示,它们相应的处理结果的关键指标如表2所示。
| 表 1 仿真实验的主要系统参数 Tab.1 Main system parameters for experiment |
|
图 4 利用传统的特征子空间法处理得到的点目标仿真实验结果 Fig.4 Imaging results of point target via traditional eigensubspace-based approach |
|
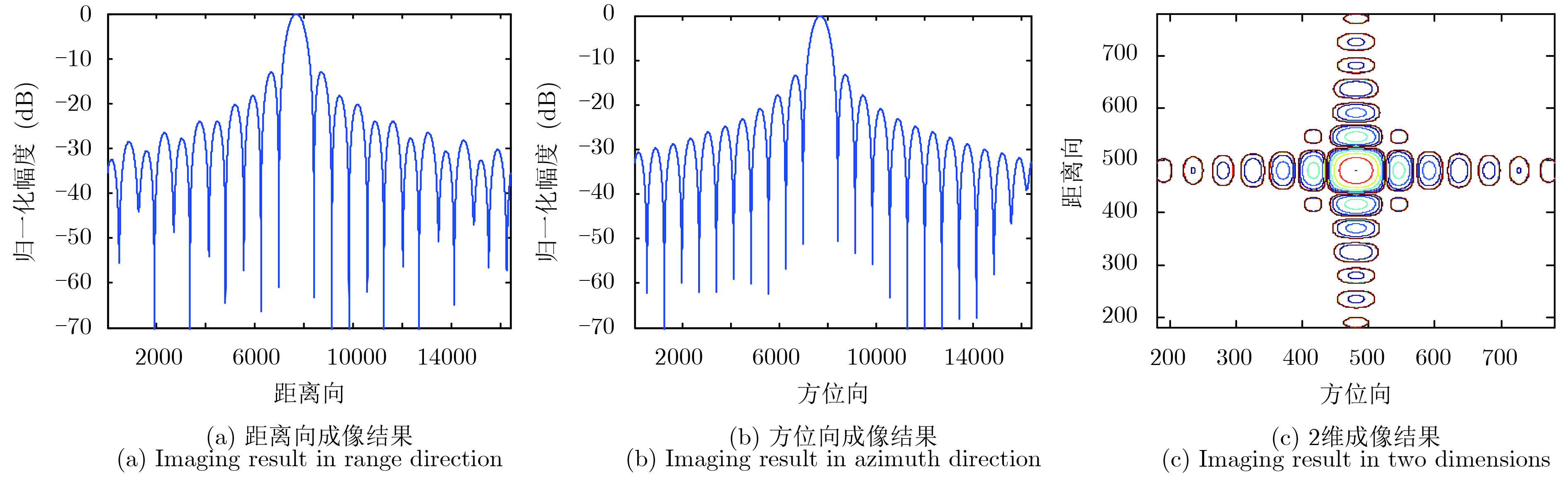
图 5 利用改进的的特征子空间法处理得到的点目标仿真实验结果 Fig.5 Imaging results of point target via modified eigensubspace-based approach |
| 表 2 距离向/方位向关键指标的仿真实验结果(dB) Tab.2 Simulation results of key indicators in range /azimuth direction (dB) |
通过对比图4和图5的点目标仿真结果,可以看出与传统的特征子空间法相比,改进的特征子空间法在距离向上旁瓣降低,显著提升成像质量。由表2可知,与传统的特征子空间法相比,改进的特征子空间法在距离向上PSLR降低了约1.5 dB,ISLR降低了约1.7 dB。经改进的特征子空间法处理后得到的PSLR和ISLR都与理想点目标的指标基本一致,进而证明了改进算法的有效性。
4.2 实测实验利用实测数据对改进的特征子空间法进一步进行验证。我们用到的L波段机载SAR实验数据由中国科学院电子学研究所提供[19]。成像场景是海岸线区域。机载实验系统的主要系统参数如表3所示。
| 表 3 机载实验系统的主要系统参数 Tab.3 Main system parameters for experiment |
完整的原始SAR图像如图6所示。我们可以从中看出整幅图像明显受到了RFI的影响,严重影响了后续的应用。

|
图 6 包含RFI的完整原始SAR图像 Fig.6 Original full SAR image containing RFI |
为了进一步证明提出的改进方法的有效性,利用实测数据进行了对比实验。首先选取图6中由红色方框标记的区域“A” ,该区域明显受到了RFI的影响;然后我们分别利用传统特征子空间法和改进的特征子空间法来对该区域(原始数据)进行处理,处理结果如图7所示。图7(a)为未进行RFI抑制的原始图像。我们可以从中看出很多亮条纹,这些亮条纹是由RFI生成的,沿距离向分布,严重影响成像质量。图7(b)为利用传统特征子空间法进行RFI抑制后的图像。可以看出RFI成功得到抑制,然而也同时丢失了很多细节信息,特别是海岸线区域。图7(c)为利用改进的特征子空间法进行RFI抑制后的图像。可以从中看出RFI成功得到抑制,同时与传统方法相比,图像中明显保留了更多的细节信息。换句话说,图7(c)的成像质量明显优于图7(a)和图7(b)。利用相同的方法对图6中的区域“B” 进行处理,可得图8,对比结果可以得到与图7相同的结论。
在运算效率方面,与传统特征子空间法相比,改进的特征子空间法可以显著提升运算效率。其原因是改进方法增加了预处理过程,选出包含RFI的距离频域方位时域数据,进而将后续处理范围限定在相对较小的数据范围内。
从理论上看,特征子空间处理中,处理的是一个2维矩阵。需要将每一个列向量分成若干段(有重叠),然后分别进行处理,最后还要还原回矩阵,运算量十分大。改进的特征子空间法只在检测出的存在干扰的部分进行特征值分解处理,可以节省大量时间。而检测算法的运算效率都很高。其中,初步RFI检测和时域RFI检测都只有几行代码。而频域RFI检测(SVR检测)处理的对象是一个向量,运算量很小,与后续干扰抑制处理相比,也可以忽略不计。
从实验结果来看,在我们的实验中,CPU型号:Intel(R) Xeon(R) CPU E5405 @ 2.00 GHz 2.00 GHz。SVR检测时间:12.871571 s。传统特征子空间法时间:40366.133685s。改进的特征子空间法时间:10442.629862 s。处理数据的尺寸为6144×32768。
理论和实验结果均可说明,新方法比传统方法运算效率更高。
5 结束语本文针对SAR图像RFI抑制,提出了一种改进的特征子空间法。在特征值分解处理之前添加了预处理模块,即在距离频域和方位时域分别进行RFI检测。与传统特征子空间法相比,改进的特征子空间法可以在更短的时间内得到更好的成像效果,即同时提高了成像效果和运算效率。改进的特征子空间法可以广泛应用于工作在低波段的SAR系统中,以便处理RFI问题。
| [1] |
Goriachkin O V. Azimuth resolution of spaceborne P, VHF-band SAR[J].
IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 251-254. DOI:10.1109/LGRS.2004.833777 ( 0) 0)
|
| [2] |
邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J].
雷达学报, 2012, 1(1): 1-10. Deng Yun-kai, Zhao Feng-jun, and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1-10. DOI:10.3724/SP.J.1300.2012.20015 (  0) 0)
|
| [3] |
Meyer F J, Nicoll J B, and Doulgeris A P. Correction and characterization of radio frequency interference signatures in L-band synthetic aperture radar data[J].
IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 4961-24972. DOI:10.1109/TGRS.2013.2252469 ( 0) 0)
|
| [4] |
Nguyen L and Soumekh M. Suppression of radio frequency inteference (RFI) for synchronous impulse reconstruction ultra-wideband radar[C]. Proceedings of SPIE 5808, Algorithms for Synthetic Aperture Radar Imagery XII, Orlando, Florida, USA, 2005: 178–184.
( 0) 0)
|
| [5] |
Ojowu Jr O O and Li Jian. RFI suppression for synchronous impulse reconstruction UWB radar using RELAX[J].
International Journal of Remote Sensing Applications, 2013, 3(1): 33-46. ( 0) 0)
|
| [6] |
Lord R T and Inggs M R. Efficient RFI suppression in SAR using LMS adaptive filter integrated with range/Doppler algorithm[J].
Electronics Letters, 1999, 35(8): 629-630. DOI:10.1049/el:19990437 ( 0) 0)
|
| [7] |
Luo X, Ulander L M H, Askne J, et al. RFI suppression in ultra-wideband SAR systems using LMS filters in frequency domain[J].
Electronics Letters, 2001, 37(4): 241-243. DOI:10.1049/el:20010153 ( 0) 0)
|
| [8] |
Ulug B. An Algorithm for Sinusoidal Interference Reduction Using Iterative Maximum Likelihood Estimation Techniques[M]. 1992.
( 0) 0)
|
| [9] |
Buckreuss S. Filtering interferences from p-band SAR data[C]. Proceedings of EUSAR’98 Conference, Frie- drichshafen, Germany, 1998.
( 0) 0)
|
| [10] |
Ruan Hang, Ye Wei, Yin Can-bin, et al.. Wide band noise interference suppression for SAR with dechirping and eigensubspace filtering[C]. Proceedings of 2010 International Conference on Intelligent Control and Information Processing, Dalian, China, 2010: 39–42.
( 0) 0)
|
| [11] |
Feng Jin, Zheng Hui-fang, Deng Yun-kai, et al. Application of subband spectral cancellation for SAR narrow-band interference suppression[J].
IEEE Geoscience and Remote Sensing Letters, 2012, 9(2): 190-193. DOI:10.1109/LGRS.2011.2163150 ( 0) 0)
|
| [12] |
Zhou Feng, Tao Ming-liang, Bai Xue-ru, et al. Narrow-band interference suppression for SAR based on independent component analysis[J].
IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 4952-4960. DOI:10.1109/TGRS.2013.2244605 ( 0) 0)
|
| [13] |
Zhou Feng and Tao Ming-liang. Research on methods for narrow-band interference suppression in synthetic aperture radar data[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(7): 3476-3485. DOI:10.1109/JSTARS.2015.2431916 ( 0) 0)
|
| [14] |
郑慧芳, 杨淋, 冯锦. SAR窄带干扰抑制的子带子空间滤波技术研究[J].
电子与信息学报, 2013, 35(12): 2836-2842. Zheng Hui-fang, Yang Lin, and Feng Jin. Research on the subband subspace filtering for narrow band interference suppression in SAR[J]. Journal of Electronics & Information Technology, 2013, 35(12): 2836-2842. DOI:10.3724/SP.J.1146.2013.00201 (  0) 0)
|
| [15] |
Smola A J and Schölkopf B. A tutorial on support vector regression[J].
Statistics and Computing, 2004, 14(3): 199-222. DOI:10.1023/B:STCO.0000035301.49549.88 ( 0) 0)
|
| [16] |
Huang Guang-bin, Zhou Hong-ming, Ding Xiao-jian, et al. Extreme learning machine for regression and multiclass classification[J].
IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2012, 42(2): 513-529. DOI:10.1109/TSMCB.2011.2168604 ( 0) 0)
|
| [17] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 128–139.
Zhou Zhi-hua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016: 128–139. (  0) 0)
|
| [18] |
Zhou Feng, Wu Ren-biao, Xing Meng-dao, et al. Eigensubspace-based filtering with application in narrow-band interference suppression for SAR[J].
IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 75-79. DOI:10.1109/LGRS.2006.887033 ( 0) 0)
|
| [19] |
Li Ning, Wang R, Deng Yun-kai, et al. Autofocus correction of residual RCM for VHR SAR sensors with light-small aircraft[J].
IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 441-452. DOI:10.1109/TGRS.2016.2608423 ( 0) 0)
|






