1 引言

合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天时、全天候的对地观测能力，在资源勘测、军事侦察、灾害监测等方面具有广泛的应用前景^[1,2]。为了提供更广阔、更精细的目标信息，SAR系统朝着高分辨率、宽测绘带的方向迅速发展，但与此同时也导致了数据量的急剧增加。

方位向多通道技术是实现高分辨率、宽测绘带的有效途径之一^[3–7]，该技术在方位向设置多个接收子孔径，能够在一个脉冲周期内获得多个回波信号，从而等效降低了系统的脉冲重复频率(Pulse Recurrence Frequency, PRF)，并且TerraSAR-X、Radarsat-2和Alos-2等星载SAR系统也都验证了其技术的可行性。相比传统的单通道SAR系统，多通道SAR系统的数据量会急剧增加，而实际系统中存储空间和数传带宽都是有限的，所以必须应用数据压缩技术减少数据量和降低数据率。

分块自适应量化(Block Adaptive Quantization, BAQ)是现今应用最广的SAR卫星原始数据压缩算法，最早应用于美国Magellan飞行器的SAR系统，它通过Lloyd-Max量化器对原始数据进行量化，根据不同的应用需求来选择压缩比^[8–12]。BAQ是一种有损压缩算法，压缩的过程中必然会引入量化噪声，进而影响图像信噪比和相位精度。因此，为了选择合适的压缩比，有必要评估BAQ算法对各种应用的影响。文献[13]分析了原始数据压缩对干涉测高精度的影响，得出对测高精度要求较高的系统，至少需要采用8:4的压缩比；文献[14]从数值实验和频谱的角度分析了数据压缩对SAR的2维分辨率的影响，得出了数据压缩并不影响其2维分辨率的结论；文献[15]分析了原始数据压缩对全极化SAR信息的影响，通过仿真实验得出了极化定标时可以采用8:4的压缩比，一般场合使用8:3压缩比的结论；文献[16]分析了原始数据压缩对星载SAR/GMTI系统测速的影响，得出对测速精度要求较高时，应选择8:4的压缩比，并且在同等压缩比下，信噪比越大，测速误差越小。现今已有不少文献研究了BAQ算法在具体应用中的性能，然而针对它在多通道SAR系统的影响分析却尚未见诸报道。

通常方位向多通道系统信号采样在方位向是非均匀的，因此需要在成像之前进行多通道重构，现今比较经典的重构方法有：系统函数法^[17]、波束形成法^[18]、频谱分解法^[19]和频率采样法^[20]。但多通道重构会导致压缩信号的信噪比衰减，为了选择合适的压缩比，有必要对多通道系统的性能变化进行全面的分析。

本文的结构如下：第2节介绍了本文的基本原理，通过建立信号模型分析了信噪比尺度因子和量化信噪比的影响因素；第3节为基于仿真和实测数据的实验及分析；最后第4节对本文进行了总结。

2 多通道数据压缩性能分析

本节首先介绍了多通道SAR系统和数据压缩的基本原理，然后分析了信噪比尺度因子和量化信噪比重构前后的影响因素。最后，为充分分析系统性能变化，本文又引入了虚假目标强度比和平均相位误差这两个评估指标。

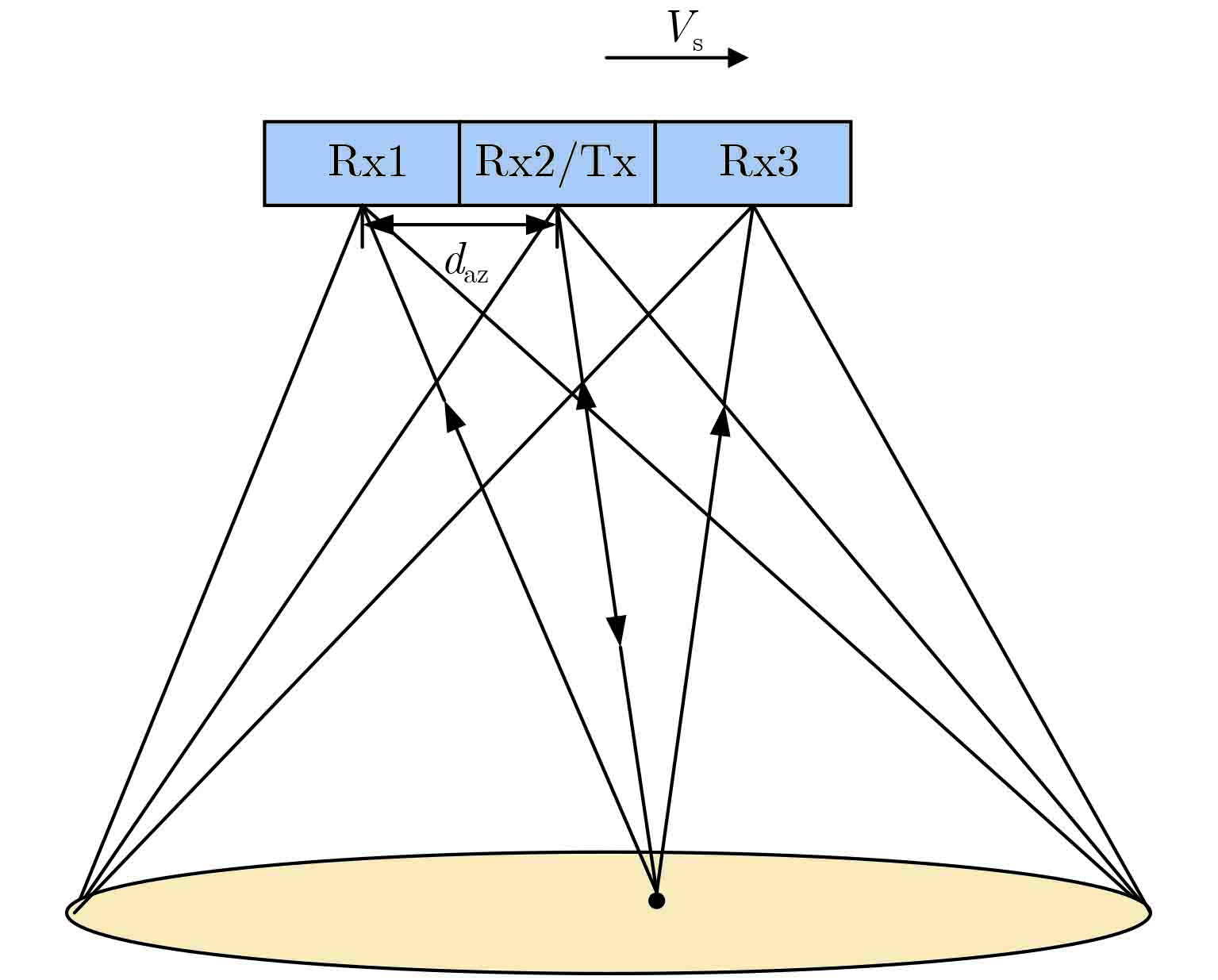
2.1 信号模型

图1为方位向多通道SAR系统的示意图，其中Rx和Tx分别表示接收子孔径和发射天线，d_az为接收子孔径相位中心间的间隔，V_s为平台速度。为了保证方位向的均匀采样，系统的PRF应满足：

${\rm{PRF}} = \frac{{2 \cdot {V_{\rm{s}}}}}{{N \cdot {d_{{\rm{az}}}}}}$

(1)

式中，N为通道数。然而在实际的SAR系统设计时，为了避开星下点回波和发射脉冲窗口的回波信号，很多情况下PRF不能满足上式。当实际系统的PRF偏离理想值时，方位向采样点将呈现周期性非均匀分布，导致方位向频谱混叠，需要在成像前进行重构处理。

BAQ算法是基于SAR原始数据统计特性，将I, Q数据分块，并对每一子块采用邻块的标准差进行归一化，然后使用Lloyd-Max量化器进行量化^[8]。作为一种有损压缩算法，BAQ算法在量化的过程中必然引入了量化噪声，进而影响系统性能。

2.2 原始回波域评估指标

(1) 信噪比尺度因子(SNR scaling factor)

非均匀采样信号需要在成像前进行重构处理，为分析数据压缩和重构过程中系统信噪比的变化，这里引入信噪比尺度因子衡量信噪比的衰减程度，其表达式为：

$\phi = \frac{{{\rm{SN}}{{\rm{R}}_{{\rm{in}}}}}}{{{\rm{SN}}{{\rm{R}}_{{\rm{out}}}}}}$

(2)

其中，SNR_in表示输入信号的信噪比，SNR_out表示输出信号的信噪比，该值越大，信噪比衰减越严重。为分析该指标，本节建立了如图2所示的信号模型，此系统为线性系统。其中 ${U_j}({f_{\rm{r}}},f)$ 为j通道的输入信号， ${n_{{\rm{t,}}j}}({f_{\rm{r}}},f)$ 为j通道的系统热噪声(每个通道的系统热噪声各不相关)，G_j为经过低噪放(LNA)后的功率增益。假设信号为非饱和的，j通道的量化噪声为 ${n_{{\rm{q}},j}}({f_{\rm{r}}},f)$ (包括采样量化噪声 ${n_{{\rm{q}},j,1}}({f_{\rm{r}}},f)$ 和数据压缩造成的量化噪声 ${n_{{\rm{q}},j,2}}({f_{\rm{r}}},f)$ ), ${P_j}({f_{\rm{r}}},f)$ 为重构滤波器， ${U_{{\rm{out}}}}({f_{\rm{r}}},f)$ 为输出信号，f_r和f分别表示距离向和方位向频率。

首先，j通道信号经过低噪放，它的信号功率和噪声功率分别为：

${P_{{\rm{s}},j}}\!\! =\!\! {P_{{\rm{tx}}.{\rm{av}}}}{G_j} \!\cdot \! E \!\! \left[ {{{\left| {{U_j}({f_{\rm{r}}},f){\rm{rect}}\! \left(\frac{{{f_{\rm{r}}}}}{B}\right)\!{\rm{rect}}\left(\frac{f}{{{I_{\rm{s}}}}}\right)} \right|}^2}} \right]$

(3)

${P_{{\rm{t}},j}} \! = {G_j}\!\cdot\! E\left[ {{{\left| {{n_{{\rm{t}},j}}({f_{\rm{r}}},f){\rm{rect}} \left(\frac{{{f_{\rm{r}}}}}{B} \right){\rm{rect}} \left(\frac{f}{{{I_{\rm{s}}}}} \right)} \right|}^2}} \right]$

(4)

其中， ${P_{{\rm{tx}}{\rm{.av}}}}$ 为信号的平均发射功率，B为距离向带宽，I_s为多普勒带宽， $E[ \cdot ]$ 表示期望值。则输入信号的信噪比为：

${\rm{SN}}{{\rm{R}}_{{\rm{in}}}} = \frac{{\displaystyle\sum\limits_{j = 1}^N {{P_{{\rm{s}},j}}} }}{{\displaystyle\sum\limits_{j = 1}^N {{P_{{\rm{t}},j}}} }}$

(5)

然后，对信号进行采样量化和数据压缩。由于多通道重构发生在方位向，接下来只考虑方位向的参数信息，此时噪声功率可以表示为：

${P_{\rm{n}}}\!\! =\!\! \sum\limits_{j = 1}^N E \left[ {{{\left| {\left({n_{{\rm{t}},j}}(f)\! \cdot\! \sqrt {{G_j}}\! + \!{n_{{\rm{q}},j}}(f)\right) \! \cdot \! {\rm{rect}} \! \left ( \!\frac{f}{{{I_{\rm{s}}}}} \!\right ) } \right|}^2}} \right]$

(6)

相对压缩造成的量化噪声，采样量化噪声对信号噪声功率的影响很小，下面的推导中忽略采样量化噪声 ${n_{{\rm{q}},j,1}}({f_{\rm{r}}},f)$ 。此时，信噪比尺度因子 $\phi $ 为：

$\begin{split}\!\! \phi & \!\!\! \!\! = \frac{{{\rm{SN}}{{\rm{R}}_{{\rm{in}}}}}}{{{\rm{SNR}}_{{\rm{out}}}^{\rm{'}}}} \\ & \! \!\!\! \! =\! \frac{{\displaystyle\sum\limits_{j = 1}^N E \left[ {{{\left| {\left({n_{{\rm{t}},j}}(f)\! \cdot \!\sqrt {{G_j}} \right)\! \cdot \!{\rm{rect}} \!\left(\displaystyle\frac{f}{{{I_{\rm{s}}}}} \!\right)} \right|}^2}} \right]}}{{\displaystyle\sum\limits_{j = 1}^N E \left[ {{{\left| {\left({n_{{\rm{t}},j}}(f)\! \cdot \!\sqrt {{G_j}}\! +\! {n_{{\rm{q}},j,2}}(f)\right)\! \cdot\! {\rm{rect}} \! \left (\frac{f}{{{I_{\rm{s}}}}} \! \right)} \right|}^2}} \right]}}\end{split}$

(7)

故数据压缩后的信噪比受到压缩量化噪声的影响而减小。

(2) 量化信噪比(SQNR)

量化信噪比是衡量数据压缩算法性能的重要评估指标，该指标反映了数据压缩对信号的影响，其值越大，数据压缩对信号的影响越小^[21]。其计算公式为：

${\rm{SQNR}} = 10 \cdot \lg \frac{{\displaystyle\sum\limits_{p = 1}^P {\sum\limits_{q = 1}^Q {|s(p,q){|^2}} } }}{{\displaystyle\sum\limits_{p = 1}^P {\sum\limits_{q = 1}^Q {|s(p,q) - g(p,q){|^2}} } }}$

(8)

其中， $s(p,q)$ 为未压缩的信号在 $(p,q)$ 处的值， $g(p,q)$ 为压缩信号在 $(p,q)$ 处的值，P和Q分别是方位向和距离向的采样点数。

在传统的单通道SAR系统中，量化信噪比随着量化比特数线性变化^[22]，其表达式为：

${\rm{SQNR}} = 6R - 1.40$

(9)

其中，R为量化比特数。鉴于该指标只与量化噪声功率和信号功率有关，本文建立了如图3所示的信号模型。

j通道采样后的信号功率和噪声功率如下式：

${P_{{\rm{s}},j}} \!=\! {P_{{\rm{tx}}.{\rm{av}}}}{G_j}\! \cdot \!E\!\!\left[ {{{\left| {{U_j}({f_{\rm{r}}},f){\rm{rect}} \! \left (\!\frac{{{f_{\rm{r}}}}}{B} \! \right ){\rm{rect}}\! \left(\!\frac{f}{{{I_{\rm{s}}}}} \! \right )} \right|}^2}} \right]$

(10)

$\!\!\!\!\!\!\!\!\!\!\! {P_{{\rm{n}},j}} = E\left[ {{{\left| {{n_{{\rm{q}},j,1}}({f_{\rm{r}}},f){\rm{rect}}\!\!\left (\frac{{{f_{\rm{r}}}}}{B}\!\right){\rm{rect}}\!\!\left(\frac{f}{{{I_{\rm{s}}}}}\!\right)} \right|}^2}} \right]$

(11)

在下面的推导中，只考虑方位向，进行数据压缩后的噪声功率为：

${P_{\rm{n}}} = \sum\limits_{j = 1}^N E \left[ {{{\left| {({n_{{\rm{q}},j,1}}(f) + {n_{{\rm{q}},j,2}}(f)){\rm{rect}} \! \left (\frac{f}{{{I_{\rm{s}}}}} \! \right)} \right|}^2}} \right]$

(12)

在量化的过程中，有 ${n_{{\rm{q}},j,1}}(f) \ll {n_{{\rm{q}},j,2}}(f)$ ，忽略采样量化噪声。此时，系统的信号功率和量化噪声功率分别为：

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {P_{\rm{s}}} = \sum\limits_{j = 1}^N {{P_{{\rm{s}},j}}} $

(13)

${P_{\rm{n}}} = \sum\limits_{j = 1}^N {E\left[ {{{\left| {{n_{{\rm{q}},j,2}}(f){\rm{rect}}\!\left(\frac{f}{{{I_{\rm{s}}}}}\!\right)} \right|}^2}} \right]} $

(14)

故重构前量化信噪比为：

${\rm{SQNR}} = \frac{{{P_{\rm{s}}}}}{{{P_{\rm{n}}}}}$

(15)

2.3 重构后的评估指标

(1) 信噪比尺度因子

数据压缩后的信号通过一个 ${P_j}(f)$ 的线性滤波器在多普勒域进行重构。鉴于此系统为一个线性系统，可以分开计算信号功率和噪声功率，此时输出的信号功率和噪声功率为：

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {P_{{\rm{s,out}}}} = {P_{{\rm{s,in}}}}$

(16)

$\begin{aligned}{P_{{\rm{n}},{\rm{out}}}} = & \sum\limits_{j = 1}^N E \Biggr[ {\biggr| {\left({n_{{\rm{t}},j}}(f) \cdot \sqrt {{G_j}} + {n_{{\rm{q}},j,2}}(f)\right)} } \\& \left. {{{\left. { \cdot {P_j}(f){\rm{rect}}\left(\frac{f}{{{I_{\rm{s}}}}}\right)} \right|}^2}} \right]\end{aligned}$

(17)

其中， ${P_{{\rm{s}},{\rm{in}}}}$ 表示输入信号功率。由于量化噪声和系统热噪声互不相关，故有：

$\begin{split}{P_{{\rm{n}},{\rm{out}}}} = &\!\!\! \sum\limits_{j = 1}^N {{G_j} \cdot E} \left[ {{{\left| {{n_{{\rm{t}},j}}(f) \cdot {P_j}(f){\rm{rect}}\left(\frac{f}{{{I_{\rm{s}}}}}\right)} \right|}^2}} \right]\\ &\!\!\! + \sum\limits_{j = 1}^N E \left[ {{{\left| {{n_{{\rm{q}},j,2}}(f) \cdot {P_j}(f){\rm{rect}}\left(\frac{f}{{{I_{\rm{s}}}}}\right)} \right|}^2}} \right]\\{\rm{ }} = & \!\!\! ({P_{{\rm{n}},{\rm{in}}}} + {P_{{\rm{n,q}}}}) \cdot \sum\limits_{j = 1}^N {E[|{P_j}(f){|^2}]} \end{split}$

(18)

其中， ${P_{{\rm{n,q}}}}$ 表示数据压缩造成的量化噪声功率， ${P_{{\rm{n,in}}}}$ 表示热噪声功率。则信噪比尺度因子 $\phi $ 为：

$\begin{aligned}\phi & = \frac{{{P_{{\rm{s,in}}}}/{P_{{\rm{n,in}}}}}}{{{P_{{\rm{s,out}}}}/{P_{{\rm{n,out}}}}}} \\ & = \frac{{{P_{{\rm{s}},{\rm{in}}}}/{P_{{\rm{n}},{\rm{in}}}}}}{{{{{P_{{\rm{s}},{\rm{in}}}}} \mathord{\left/ {\vphantom {{{P_{{\rm{s}},{\rm{in}}}}} {\left( {({P_{{\rm{n}},{\rm{in}}}} + {P_{{\rm{n}},{\rm{q}}}}) \cdot \displaystyle\sum\limits_{j = 1}^N {NE[|{P_j}(f){|^2}]} } \right)}}} \right.} {\left( {({P_{{\rm{n}},{\rm{in}}}} + {P_{{\rm{n}},{\rm{q}}}}) \cdot \displaystyle\sum\limits_{j = 1}^N {NE[|{P_j}(f){|^2}]} } \right)}}}} \\ & = \frac{{({P_{{\rm{n,in}}}} + {P_{{\rm{n,q}}}}) \cdot \displaystyle\sum\limits_{j = 1}^N {E[|{P_j}(f){|^2}]} }}{{{P_{{\rm{n,in}}}}}} \\ &= \frac{{({P_{{\rm{n,in}}}} + {P_{{\rm{n,q}}}}) \cdot \displaystyle\sum\limits_{j = 1}^N {\sum\limits_{m = 1}^N {|{P_{jm}}(f){|^2}} } }}{{{P_{{\rm{n,in}}}}}}\end{aligned}$

(19)

文献[6]指出 ${\rm{|}}{P_{jm}}(f){\rm{|}}$ 是一个由系统PRF决定的值，并从矩阵论的角度给出重构滤波器项的数学解释，见式(20)。它表示为矩阵 ${{P}}(f) \cdot {{{P}}^{\rm{H}}}(f)$ 特征值 $\lambda ({\rm{PRF}})$ 和的形式，其中 ${{P}}(f)$ 是N通道SAR系统的重构滤波器， ${{{P}}^{\rm H}}(f)$ 为 ${{P}}(f)$ 的共轭矩阵。

$\sum\limits_{j = 1}^N {E[|{P_j}(f){|^2}]} = \sum\limits_{j = 1}^N {{\lambda _j}({\rm{PRF}})} $

(20)

故重构后信噪比尺度因子是由3部分共同作用的：压缩量化噪声功率 ${P_{{\rm{n,q}}}}$ 、系统热噪声功率 ${P_{{\rm{n,in}}}}$ 以及重构滤波器项 $\displaystyle\sum\nolimits_{j = 1}^N\!\! {E[|{P_j}(f){|^2}]} $ 。压缩量化噪声功率与系统压缩比的选择有关，压缩比越高，数据压缩造成的量化噪声越小，压缩量化噪声功率也就越小；重构滤波器项由系统PRF决定，受到系统非均匀性的影响，非均匀性越大，该项对信噪比尺度因子的影响也就越大。

(2) 量化信噪比

经过重构后，量化噪声功率的表达式如下：

${P_{\rm{n}}} = \sum\limits_{j = 1}^N E \left[ {{{\left| {{n_{{\rm{q}},j,2}}(f){\rm{rect}}\!\left (\frac{f}{{{I_{\rm{s}}}}}\!\right) \cdot {P_j}(f)} \right|}^2}} \right]$

(21)

故此时量化信噪比的表达式如下：

$\begin{aligned}{\rm{SQNR}} = & \frac{{{P_{\rm{s}}}}}{{{P_{\rm{n}}}}} = \frac{{{P_{{\rm{s,in}}}}}}{{{P_{{\rm{n,q}}}} \cdot \displaystyle\sum\limits_{j = 1}^N {E[|{P_j}(f){|^2}]} }} \\ = & \frac{{{P_{{\rm{s,in}}}}}}{{{P_{{\rm{n,q}}}} \cdot \displaystyle\sum\limits_{j = 1}^N {{\lambda _j}({\rm{PRF}})} }}\end{aligned}$

(22)

式中，分子为信号功率，对固定的系统，它是一个定值；分母由压缩量化噪声和系统的非均匀性共同决定。由此可见，影响重构后量化信噪比的因素主要有两点：压缩比和系统的非均匀性。

2.4 其他性能评估指标

(1) 虚假目标强度比(PGR)

如果不进行信号的非均匀重构或者重构不当，则将造成脉冲压缩的主峰两侧存在虚假峰值。此外，如果多通道间存在幅度和相位的不一致误差，则也会引入虚假目标。虚假目标强度比是衡量多通道成像的重要性能指标，其定义为：

${\rm{PGR}} = 20\lg \!\left(\frac{{{P_1}}}{{{P_2}}}\!\right) $

(23)

其中，P₁为虚假目标峰值幅度，P₂为真实目标峰值幅度。

(2) 平均相位误差(MPE)

该指标衡量压缩过程中引入相位误差的平均水平。其值越小表示数据压缩对相位的影响越小。其定义为：

${\rm{MPE}} = \frac{1}{{P \cdot Q}}\sum\limits_{p = 1}^P {\sum\limits_{q = 1}^Q {|\phi (p,q) - \varphi (p,q)|} } $

(24)

其中， $\phi (p,q)$ 为压缩前信号的相位， $\varphi (p,q)$ 为压缩后信号的相位。

3 实验结果与分析

为了验证上述分析的正确性，下文首先用仿真实验研究了数据压缩对信噪比尺度因子、量化噪声和虚假目标强度比的影响，然后采用实际机载数据在数据域和图像域验证了理论分析和仿真实验结果的正确性。

3.1 仿真实验及分析

实验模拟了星载多通道SAR系统的回波信号，并在各个通道加入固定信噪比的高斯白噪声作为系统热噪声。这里定义一个参数表示系统非均匀性的大小，称作非均匀因子F：

$F = \left| {\frac{{{\rm{PRF - PR}}{{\rm{F}}_{{\rm{uni}}}}}}{{{\rm{PR}}{{\rm{F}}_{{\rm{uni}}}}}}} \right|$

(25)

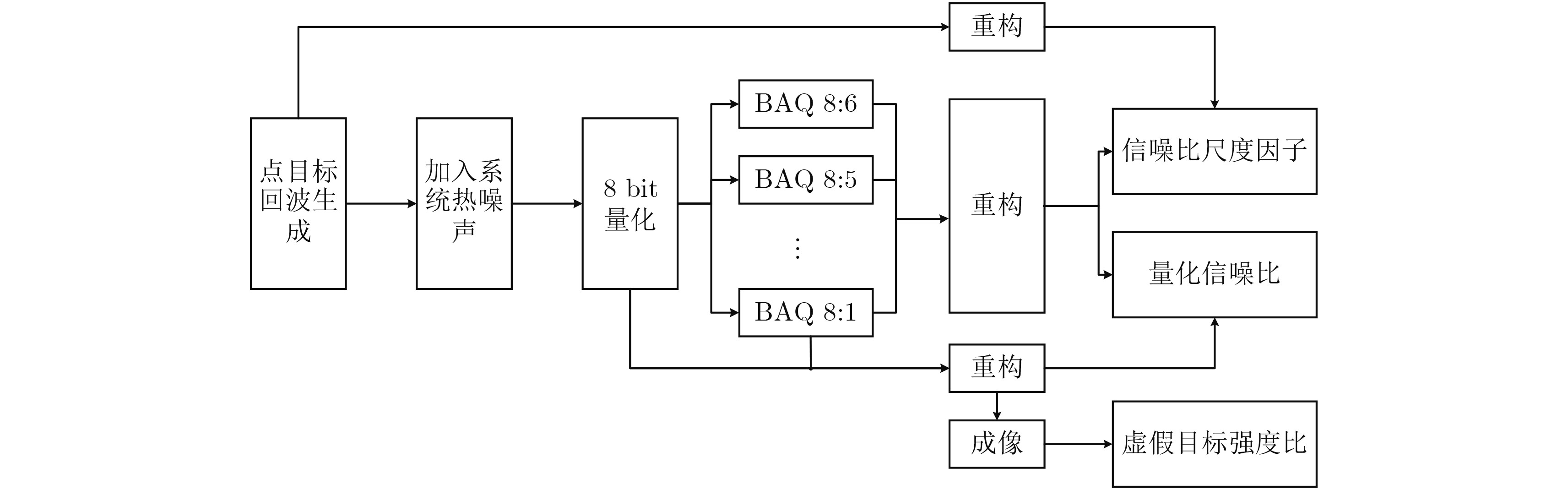
其中，PRF_uni为方位向信号均匀采样的PRF，可由式(1)计算得到。当非均匀因子为零时，表示信号均匀采样，通过调整参数，仿真实验模拟了不同非均匀因子的情况。回波数据采用8 bit量化，BAQ选择的压缩比为8:6, 8:5, 8:4, 8:3, 8:2, 8:1，重构算法选取了Kreiger在文献[17]中提出的方法，仿真参数如表1，具体的仿真实验流程如图4所示。

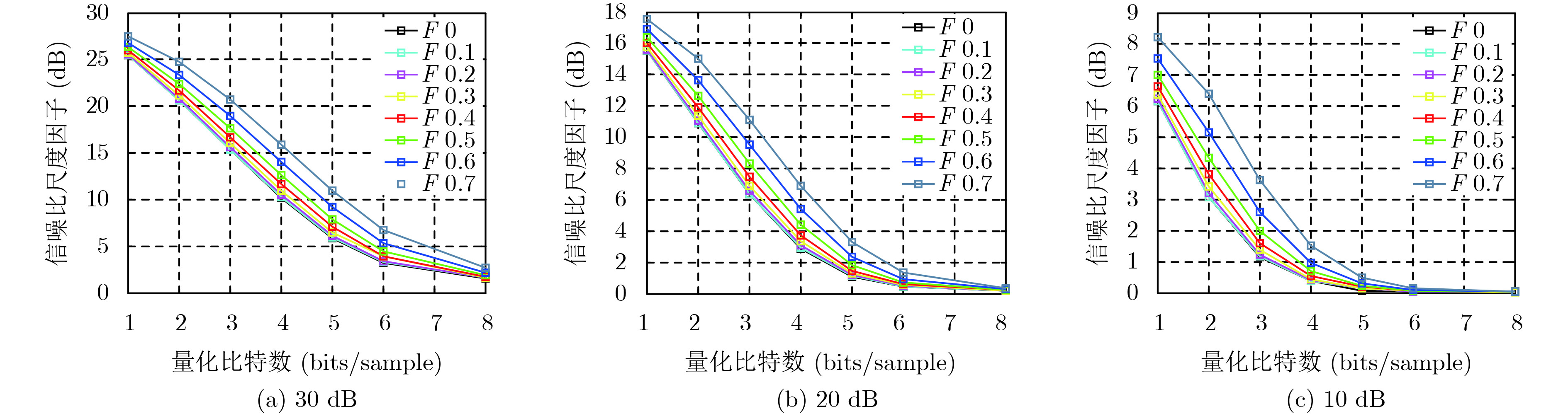
对信噪比尺度因子的仿真结果如图5所示，其中图5(a)–图5(c)的输入信号信噪比分别为30 dB, 20 dB, 10 dB。可以看出，在非均匀因子和系统热噪声相同时，随着压缩比的减小，信噪比尺度因子也随之减小；在压缩比和系统热噪声相同时，随着非均匀因子的增大，信噪比尺度因子随之增大。故信噪比尺度因子由3部分共同作用：非均匀因子，压缩比以及系统热噪声，符合2.3节理论推导的结果。

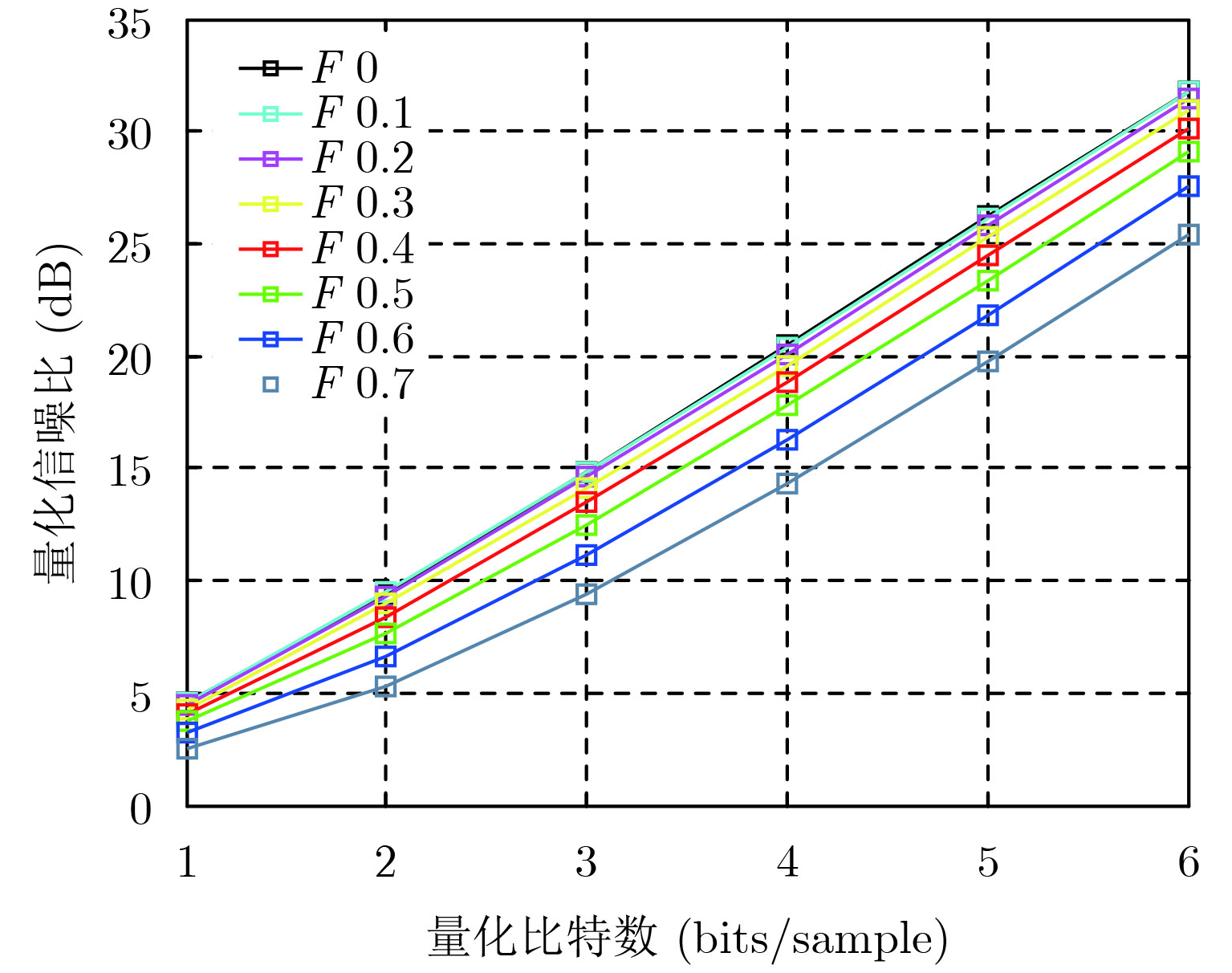
数据域量化信噪比的仿真结果如图6所示，可见：数据域量化信噪比受到压缩比和非均匀因子的影响，当非均匀因子一定时，量化信噪比与压缩比有关，压缩比越小，量化信噪比越高；当压缩比一定时，非均匀因子越大，量化信噪比越低，与2.3节理论分析基本一致。

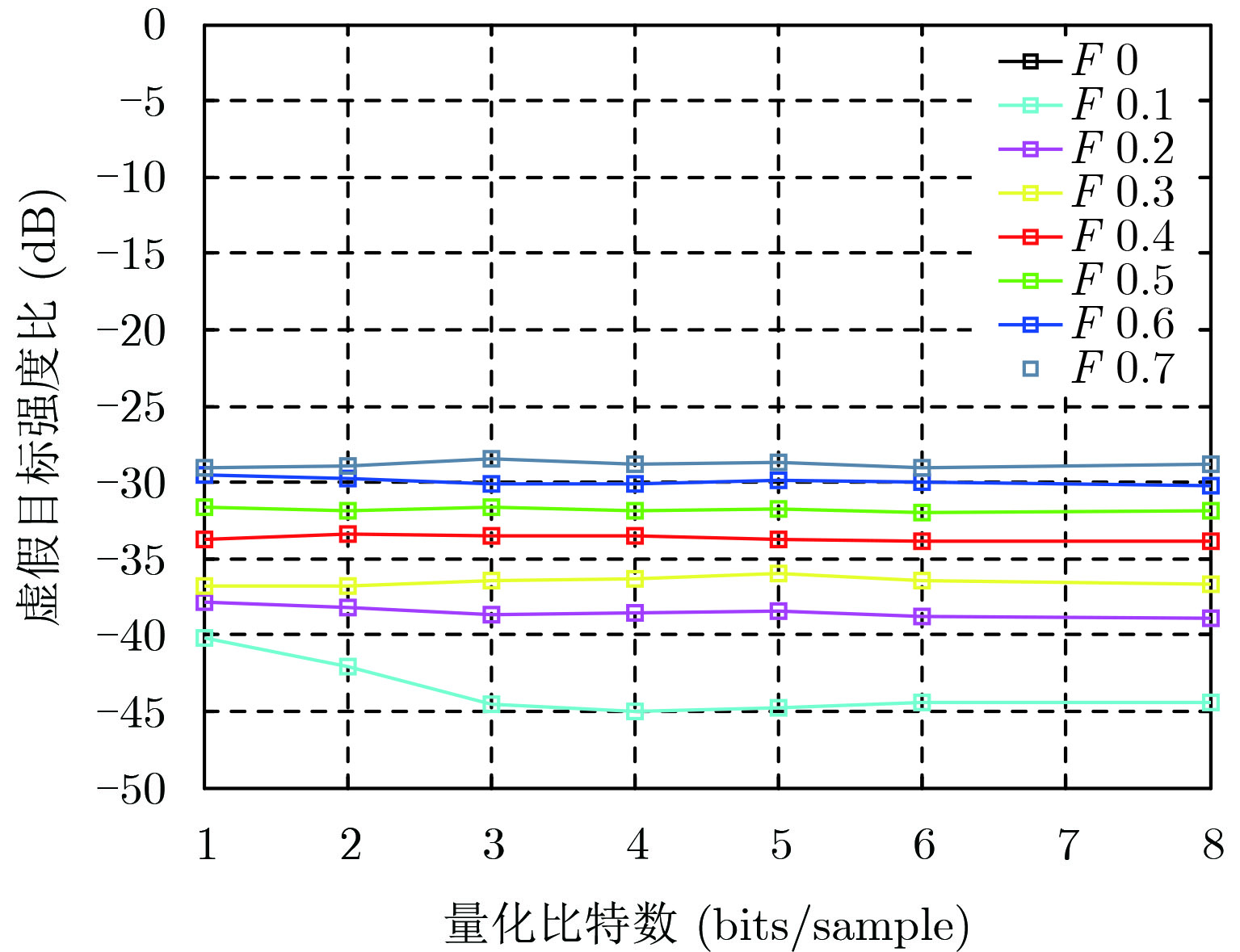
虚假目标强度比的仿真结果如图7所示，可见：(1)当非均匀因子增大时，虚假目标强度比会增大^[23]。(2)当非均匀因子一定时，采用不同的压缩比对虚假目标强度比几乎没有影响。实际上，BAQ压缩后的点目标峰值幅度衰减，但是主旁瓣相对关系不变，呈等比例衰减^[24]。故非均匀采样信号在BAQ压缩及重构的过程中，真实目标和虚假目标幅度等比例衰减，虚假目标强度比基本一致。(3)在非均匀因子较小时，选取高的压缩比可能会引起虚假目标强度比的升高，这是由于此时虚假目标本身较弱，可能会淹没在量化噪声中。

3.2 实测数据实验及分析

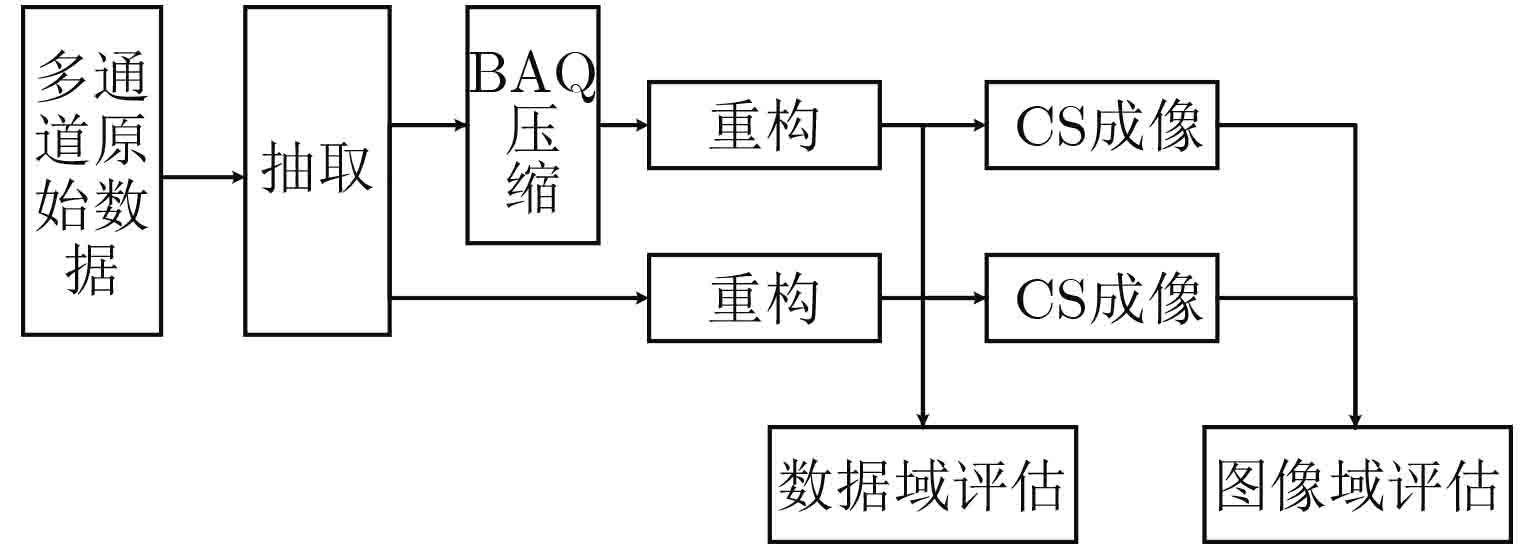
实测数据实验流程图如图8所示。本文的原始数据来自于一次飞行的四通道机载SAR系统，其系统参数如表2。此处截取了4个后向散射特性不同的均匀场景：农场、山丘、森林、海陆交界。为了评估多通道系统非均匀采样的影响，本节通过抽取的方式获得不同的PRF(300 Hz, 360 Hz和450 Hz)以获得不同的非均匀性。其原始数据为8 bit量化，虚实部都满足均值为零的高斯分布。对原始数据采用两种处理方式：一是直接进行重构处理；二是进行BAQ压缩后进行重构处理，本节依然选取3.1节中的重构方法。最后，采用Chirp Scaling算法(CSA)对重构后的数据进行聚焦，得到复图像。

下面是实测数据实验结果及分析，4种不同的场景如图9所示。其数据域量化信噪比的分析如下。

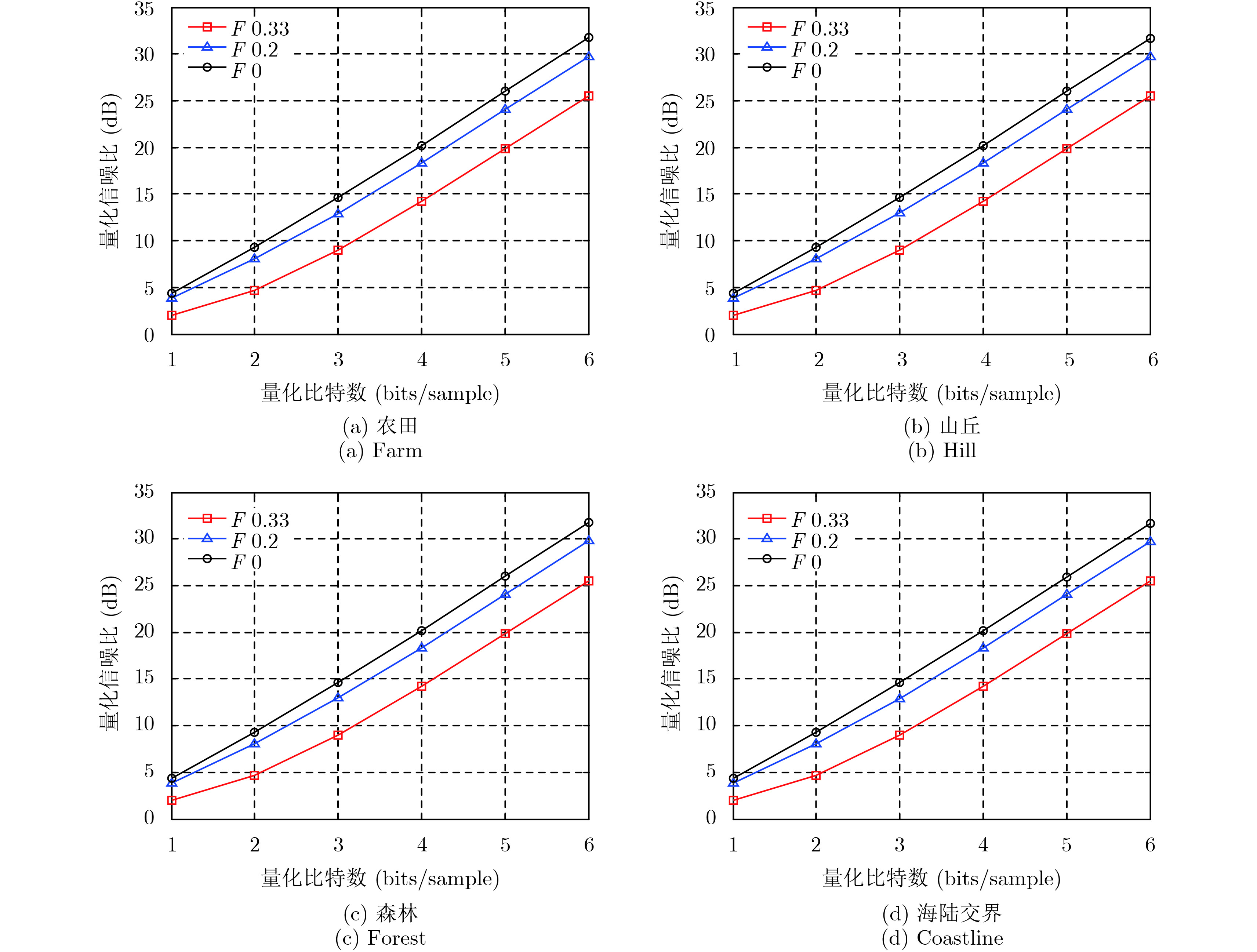
图10为4种不同场景数据域量化信噪比随量化比特数的变化曲线，图中黑色表示均匀采样的结果，红色和蓝色分别表示非均匀因子为0.33和0.2的结果。可见：(1)均匀场景的数据域量化信噪比主要与两个因素有关：非均匀因子和压缩比。非均匀因子与具体的系统参数有关，压缩比是由星上存储能力、下传链路大小以及具体应用的精度需求来综合选择的。(2)在数据域，不同场景量化信噪比均随着量化比特数线性变化，且在非均匀因子与压缩比相同时，不同场景的量化信噪比大致相等。相对均匀采样的数据，当非均匀因子为0.2时，量化信噪比衰减2 dB；当非均匀因子为0.33时，量化信噪比衰减6.2 dB。根据公式(9)所示，在非均匀因子为0.33时，若要达到均匀采样条件下8:4压缩的性能，则可能需要选择8:5的压缩比进行BAQ压缩。(3)在压缩比一定的条件下，数据域量化信噪比的衰减与非均匀因子呈非线性关系，非均匀因子越大，量化信噪比衰减越快。实测数据结果与前文量化信噪比的理论分析基本一致。

经过以上的推导，多通道SAR系统的回波信号经过重构后信噪比会下降，选用传统单通道的压缩比可能无法保持其原有的精度。现今干涉、极化等应用对相位精度的要求更高，所以需要对信号的相位变化进行精准评估，此处选取平均相位误差作为评估指标。

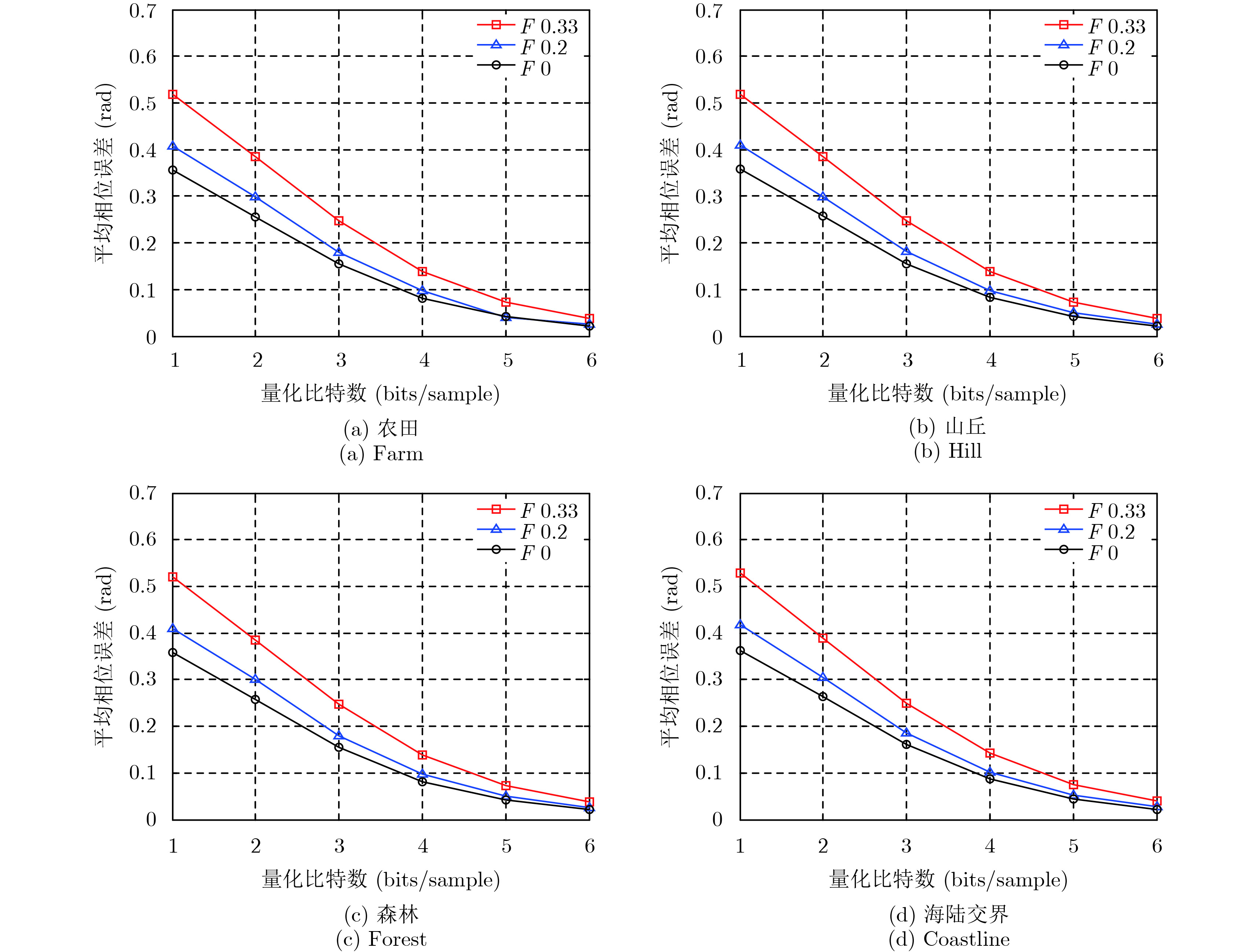
图11展示了平均相位误差在数据域的结果。可见：均匀场景数据域的平均相位误差也主要与压缩比和非均匀因子有关。非均匀因子越大，平均相位误差也就越大。在数据域，以8:4压缩的数据为例，均匀采样时，平均相位误差为0.082 rad；当非均匀因子为0.2时，平均相位误差为0.097 rad；当非均匀因子为0.33时，平均相位误差为0.138 rad，若要达到均匀采样条件下8:4压缩的相位精度，则需要选择8:5的压缩比。

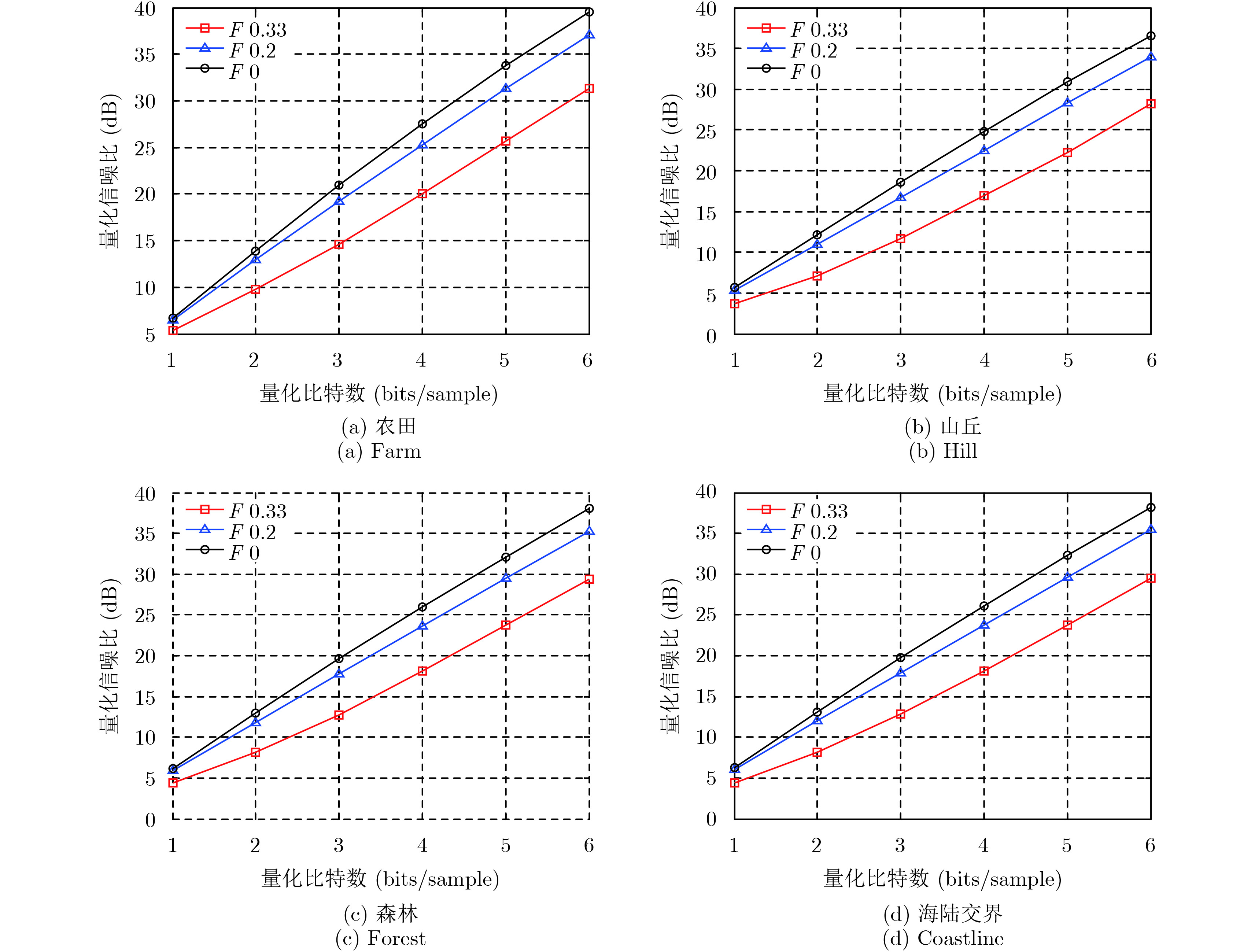
量化信噪比和平均相位误差还可作为图像域评估指标，图12展示了图像域量化信噪比的结果，可见：(1)图像域的量化信噪比不仅与非均匀因子和压缩比有关，还与场景有关，如在非均匀因子为0.2，压缩比为8:4的情况下，场景(a)为25.3 dB，场景(b)为22.9 dB，场景(c)为23.6 dB，场景(d)23.5 dB，可见场景目标的后向散射特性影响图像域的量化信噪比。(2)图像域的量化信噪比依然与量化比特数满足线性关系。

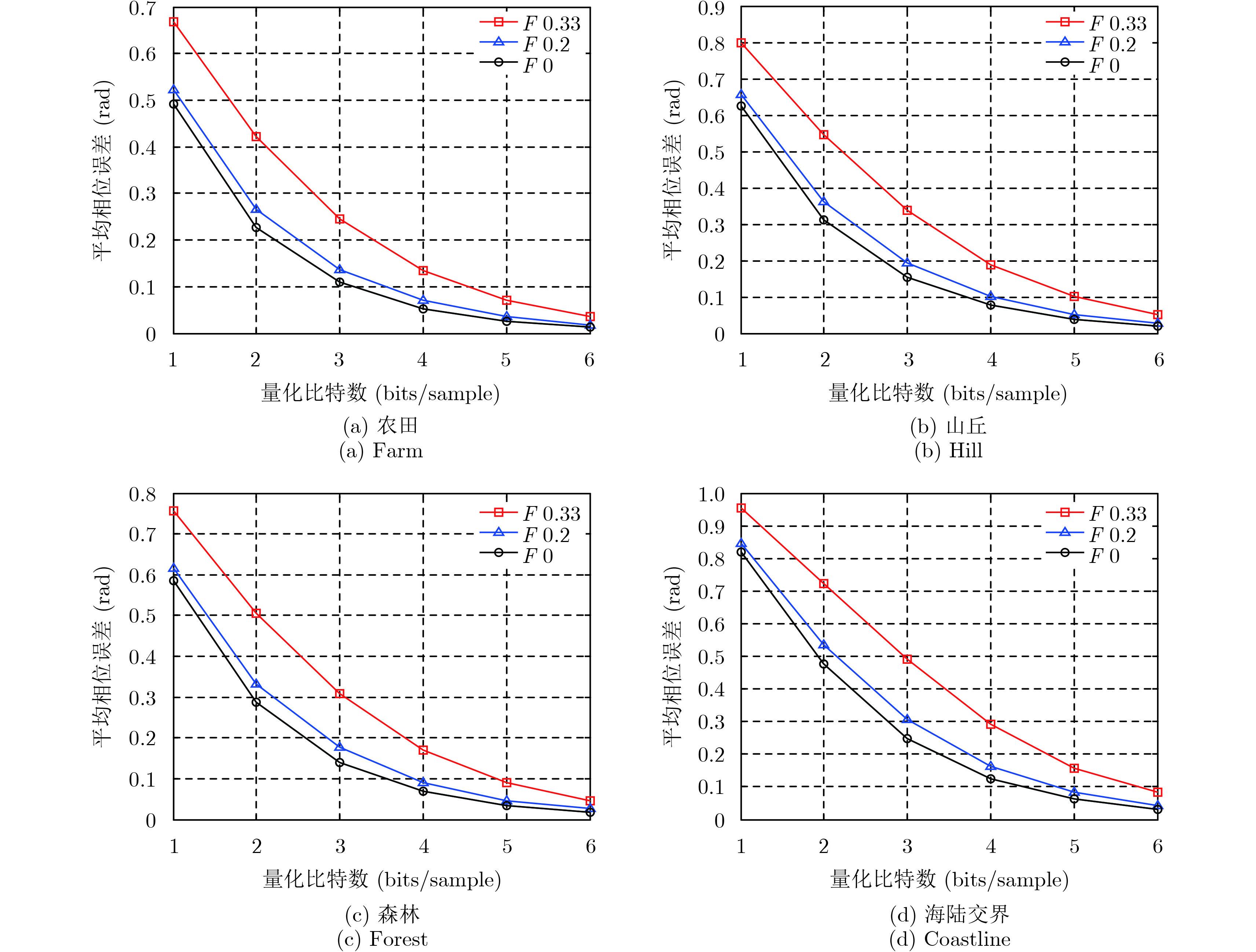
图像域的平均相位误差结果如图13所示，可见：(1)图像域的平均相位误差与量化信噪比的影响因素相同。当压缩比为8:4、非均匀因子为0.2时，4个场景的平均相位误差依次为：场景(a)0.070 rad，场景(b)0.102 rad，场景(c)0.091 rad，场景(d)0.162 rad。场景(d)的平均相位误差与其余3个场景相差较大，实际上，对散射强度不同的区域，低散射区域的回波信号经过BAQ压缩后相位损失较大^[11]。海陆交界的场景中有既有陆地又有海面，海面相对陆地，它的散射强度较低，故场景(d)平均相位误差相对较大。(2)图像域的平均相位误差与量化比特数之间呈非线性关系，此外随着量化比特数的提高，非均匀因子对相位的影响越来越小。

4 结论

本文分析了数据压缩对方位向多通道SAR系统的影响，建立了多通道数据压缩的信号模型，推导并分析了对数据域量化信噪比和信噪比尺度因子的影响因素，最后通过仿真和实测数据，在数据域和图像域分析了量化信噪比、平均相位误差的实验结果。结果表明：信噪比尺度因子受到系统热噪声、压缩比和非均匀因子三者的制约；数据压缩基本不影响虚假目标强度比；经过BAQ压缩的非均匀采样信号在重构的过程中量化信噪比会衰减，系统的非均匀因子越大，重构滤波器项对量化噪声的影响越大，量化信噪比衰减得越严重，BAQ算法性能将进一步下降；在均匀场景的数据域，数据压缩对系统性能的影响因素主要有两点：非均匀因子和压缩比；在图像域，其影响因素还包括地面散射特性。在进行实际SAR系统的压缩算法设计时，如表2中所示参数，当非均匀因子为0.2或者更小时，采用8:4能满足系统高精度应用的需求；当非均匀因子为0.33或者更高时，则要采用更低的压缩比(如8:5)才能满足此需求。在非均匀因子较大时，BAQ算法性能将会严重下降，未来的工作是根据通道间相干性研究高性能的数据压缩算法，以期在保证图像质量的同时尽可能的减少数据量。