② (中国科学院大学 北京 100039)
② (University of Chinese Academy of Sciences, Beijing 100039, China)
作为重要的对地观测传感器,合成孔径雷达(Synthetic Aperture Radar, SAR)具备全天时、全天候、不受气候条件影响甚至穿透植被与地表的成像能力,被广泛用于高分辨率对地成像;相比机载SAR,星载SAR的单次成像测绘带宽可达上百公里,且成像区域不限制于领空主权,因此在全球地形测绘、军事侦察等领域具有难以替代的作用[1–3]。星载SAR系统有两个重要技术指标——分辨率与测绘带宽:高分辨率可获得更多的目标信息,有利于后续处理中的目标检测和识别;宽测绘带可缩短重复观测周期,有利于对热点地区进行空间监视[3]。因此,同时实现高分辨率和宽测绘带成像成为星载SAR的重要发展方向。受星载SAR系统最小天线面积限制[4]的束缚,传统模式的星载SAR难以同时实现高分辨率宽测绘带成像,要实现这一目标需要另辟蹊径。
方位向多通道技术是解决这一问题的有效手段[5–7]。它在方位向以一个小孔径发射低脉冲重复频率(Pulse Repetition Frequency, PRF)信号实现大测绘带,同时方位向设置多个接收孔径接收信号以提高采样率,从而巧妙缓解了星载SAR的最小天线面积限制,但是仅当PRF满足均匀采样条件时方位向信号采样才是均匀的,系统PRF被锁定在一个固定值上[8]。但是在系统设计中,PRF选择的灵活性非常重要。当PRF不满足均匀采样条件时,系统方位向信号的采样是非均匀的,会出现方位向的频谱混叠并导致方位模糊,如果不做处理直接成像会大大降低成像质量。因此,方位向非均匀采样信号重建成为一项有意义的工作。
发展至今,许多方法[8–15]被提出用于解决方位向多通道星载SAR系统信号非均匀采样重建问题。基于广义采样定理,德国宇航中心学者提出了滤波器组重建算法[8],它将方位向多通道回波信号表述为经独立线性系统滤波后的输出,进而设计相应的重构滤波器对信号进行重建;另外一种广泛使用的方法是由我国学者提出的空时自适应处理[10],它利用混叠频率的不同空域信息将混叠频率分离实现信号重建。很多方法基于以上两种方法提出,包括基于信号子空间投影提高算法鲁棒性的改进[11]以及最小化均方误差代价函数的修正[12]等。文献[13]对各种改进的方法进行了对比。文献[14]的方法基于周期非均匀采样信号重建理论,由于涉及到非均匀离散傅里叶变换(NonUniform Discrete Fourier Transform, NUDFT),该算法运算复杂度较高,文献[15]基于非均匀快速傅里叶变换(NonUniform Fast Fourier Transform, NUFFT)对其进行了改进。
本文创新性地提出以数字图像处理(Digital Image Processing, DIP)领域多帧超分辨率[16–20]的思路解决方位向多通道星载SAR非均匀采样信号重建问题,推导了一种频域超分辨处理方法,并总结给出了多帧超分辨处理的一般方法。仿真与实测数据实验表明,本文方法能有效消除方位向非均匀采样造成的模糊,并且在复杂度性能上具有一定的优势。本文第1次证明了方位向多通道星载SAR系统信号非均匀采样重建问题可以被看作一个多帧超分辨率问题,并给出了多帧超分辨处理的一般方法。由于多帧超分辨率是DIP领域的研究热点,有许多成熟算法可供借鉴,从而为方位向多通道星载SAR系统信号非均匀采样重建问题的解决提供一种新的思路。
文章第2节在介绍超分辨率概念与方位向多通道系统原理的基础上,建立多帧超分辨问题与方位向多通道系统非均匀采样信号重建问题的联系;第3节首先建立一种简单的图像(信号)退化模型,之后对模型进行可逆描述并在逆推模型中实现多帧超分辨处理,最后总结给出多帧超分辨处理的一般方法;第4节结合仿真与实测数据实验验证了本文思路与方法的有效性;第5节分析了滤波器组方法与本文方法的复杂度,证明本文方法在复杂度性能上的优势;第6节对该文进行总结。
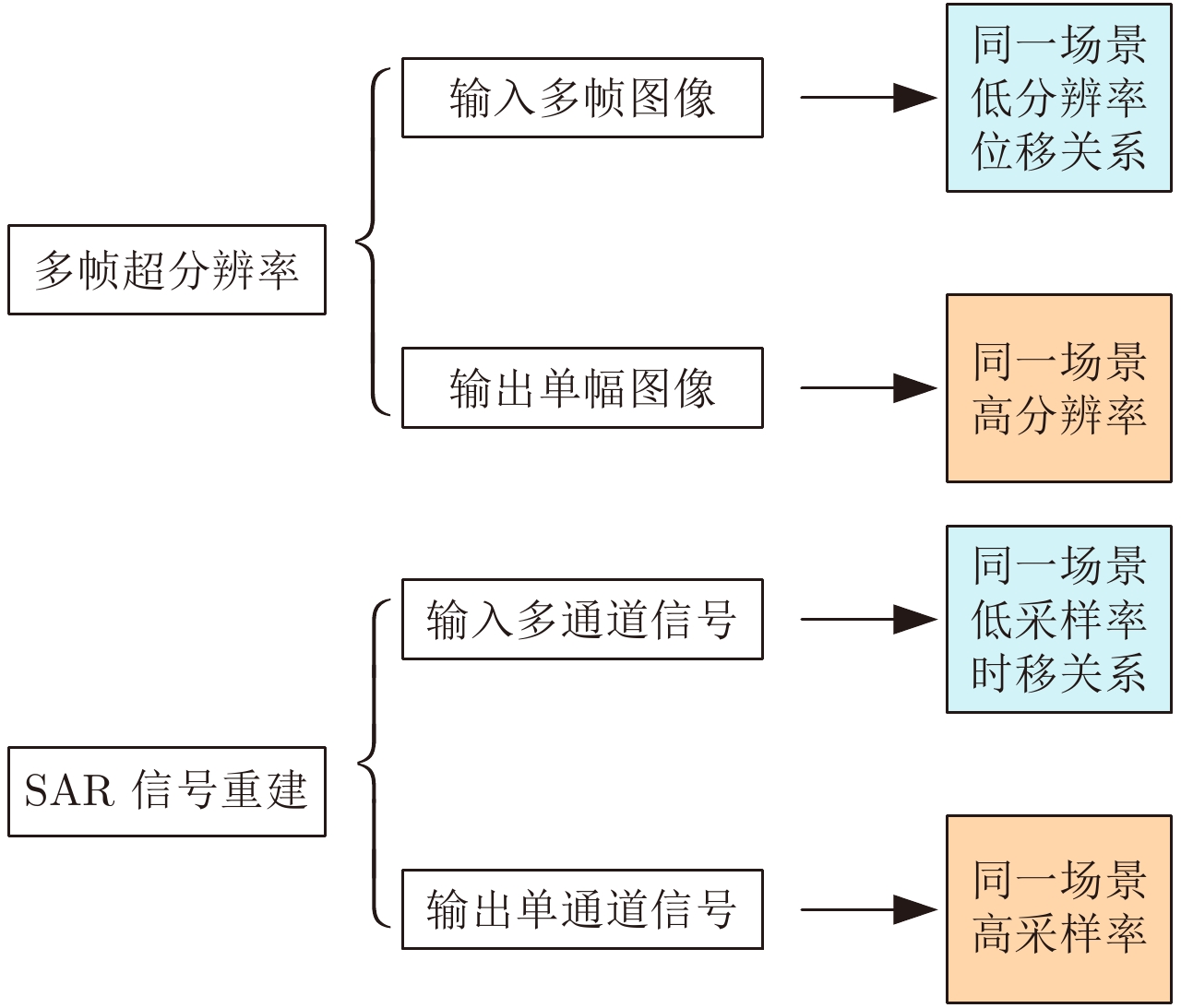
2 多帧超分辨率与方位向多通道系统信号重建 2.1 超分辨率概念本节对DIP领域的超分辨率问题进行简单介绍。图像的超分辨率是指用图像处理方法,以软件算法的形式将输入低分辨率图像转换为高分辨率图像输出的技术[17]。图像的超分辨率问题可大致分为单帧图像的超分辨率问题和多帧图像的超分辨率问题。如图1(a)所示,单帧图像的超分辨率问题即通过输入一幅低分辨率的图像,经过信号处理过程获取同一场景的高分辨率图像,输出图像中包含了输入图像中没有的信息。多帧图像超分辨率问题的输入是同一场景的一系列低分辨率帧,这些不同的图像之间满足一定的关系,例如是由位于不同位置的多个相机(成像系统)对同一场景成像得到,输出是这一场景的高分辨率图像, 如图1(b)所示。此时输出图像可以利用输入图像信息经信号处理得到。严格来讲,多帧超分辨率由于没有“生成”信息,概念里的“超”分辨可能在某些场合不被完全承认,但这一概念在DIP领域已被使用并认可数十年,为避免混淆,我们仍沿用这一概念。本文将重点放在多帧图像的超分辨处理上,并在2.3节证明方位向多通道系统非均匀采样信号重建问题可以被看作一个多帧超分辨率问题。

|
图 1 单帧及多帧超分辨率模型 Fig.1 Model for single image and multiframe super resolution |
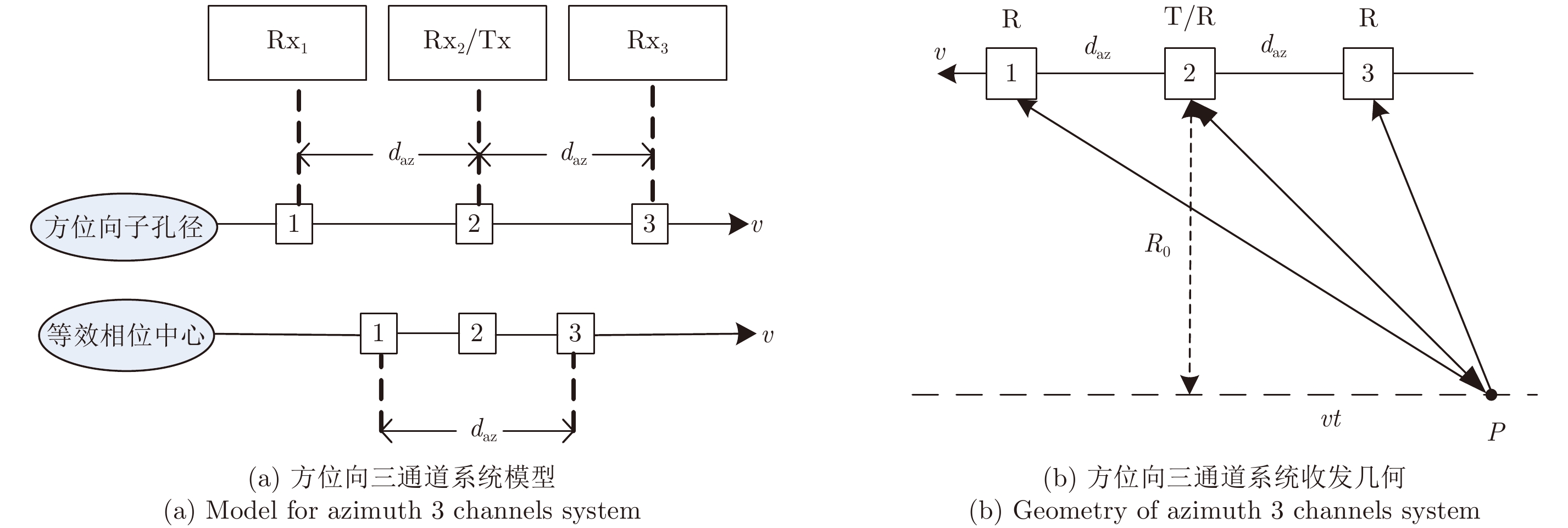
为简化分析并突出主要步骤,在下面的讨论中只考虑方位向信号。图2是典型方位向三通道系统模型与收发几何,它的中间孔径为发射和接收孔径,其余孔径为接收孔径,即实现方位向的一发三收。如果t=0时发射孔径正好位于目标正上方,根据图2(b)的收发几何,对于单个点目标,回波信号可表示为:
|
$\begin{aligned}{s_i}\left( t \right) =& {A_{{\rm{Tx}}}}\left( {vt} \right) \cdot {A_{{\rm{Rx}},i}}\left( {vt} \right)\\ \cdot \!& \exp \!\left\{ {\!\! - {\rm{j}}\frac{{2{π} }}{\lambda }\!\! \left( { \!\!\! \sqrt {R_{\rm{0}}^{\rm{2}} \!+\! \!{{\left( {vt} \right)}^2}} \!\!+\!\! \sqrt {R_{\rm{0}}^{\rm{2}} \!+\!\! {{\left( {vt \!-\! \Delta {x_i}} \right)}^2}} } \right)} \! \right\}\end{aligned}$
|
(1) |
|
图 2 方位向三通道系统模型与收发几何 Fig.2 Model and geometry for azimuth 3 channels system |
其中,
|
$\begin{aligned}\!\!\!\!\!{s_i}\left( t \right) \approx & {A_{{\rm{Tx}}}}\left( {vt} \right) \cdot {A_{{\rm{Rx}},i}}\left( {vt} \right) \cdot \exp \left\{ { - {\rm{j}}\frac{{4{π} }}{\lambda }{R_{\rm{0}}}} \right\}\\& \cdot \! \exp \! \left\{ {\!\! - {\rm{j}}\frac{{{π} \Delta x_i^2}}{{2\lambda {R_{\rm{0}}}}}} \right\} \!\\ & \cdot\! \exp \left\{ {\!\! - {\rm{j}}\frac{{2{π} {v^2}}}{\lambda } \! \displaystyle \frac{{{{\left( {t - \displaystyle \frac{{\Delta {x_i}}}{{2v}}} \right)}^2}}}{{{R_{\rm{0}}}}}}\! \right\}\end{aligned}$
|
(2) |
对于传统单通道系统,其点目标回波如下:
|
$\begin{split}s\left( t \right) \approx & \!\!\!\!{A_{\rm{Tx}}}\left( {vt} \right) \cdot {A_{\rm{Rx}}}\left( {vt} \right) \cdot \exp \left\{ { - {\rm{j}}\frac{{4{π} }}{\lambda }{R_{\rm{0}}}} \right\}\\ &\!\!\!\! \cdot \exp \left\{ { - {\rm{j}}\frac{{2{π} {v^{\rm{2}}}{t^2}}}{{\lambda {R_{\rm{0}}}}}} \right\}\end{split}$
|
(3) |
对比式(2)与式(3),对于单平台系统,由于
|
${\rm{PRF}} = \frac{{2v}}{{p \cdot {d_{{\rm{az}}}}}}$
|
(4) |
这意味着对于已知的系统,PRF必须取固定值,任何不满足均匀采样条件的取值将导致方位向接收信号的非均匀采样,从而导致信号频谱的模糊。我们期望此时能将混叠的频谱进行重建以获得方位向均匀采样的信号。
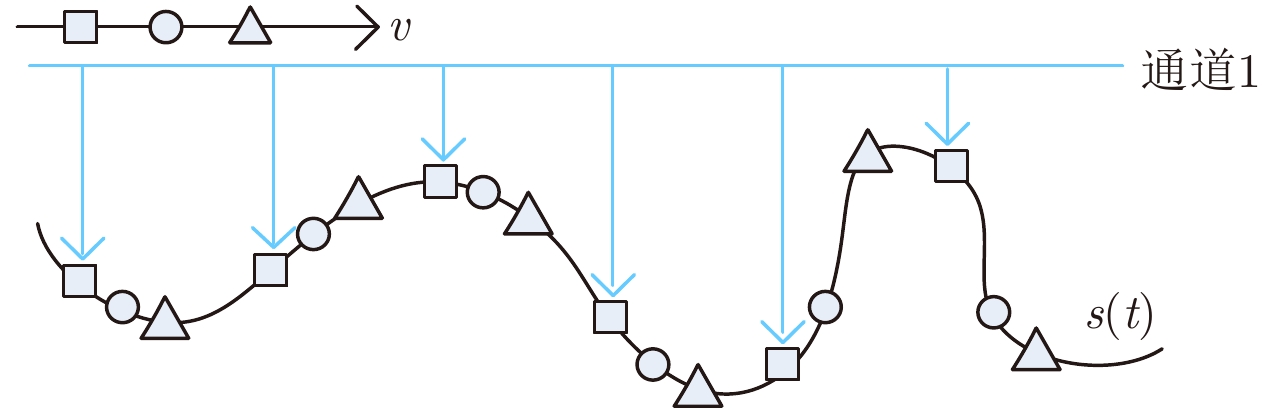
2.3 信号重建与多帧超分辨率的相似性分析无论对于方位向多通道系统还是传统单通道系统,由回波反映的地面特性是一个未知的连续时间信号,由于SAR的脉冲工作方式,方位向的接收信号被采样为离散信号。图3示意了方位向三通道系统的采样场景,此时PRF不满足均匀采样条件。
|
图 3 方位向三通道系统采样场景 Fig.3 The sampling scenario of anazimuth 3 channels system |
图示的3个通道获得了
|
图 4 多帧超分辨率与多通道SAR信号重建对比 Fig.4 Comparison of multiframe super resolution and signal reconstruction of multichannel SAR system |
由于输入输出在信号特性上的高度相似性,方位向多通道系统非均匀采样信号的重建问题可以看作类多帧超分辨率问题,在超分辨处理中可实现方位向信号的均匀化重建。下一节对一种频域超分辨方法在信号重建问题中的适用性进行推导,并总结给出多帧超分辨处理的一般方法。
3 多帧超分辨方法用于方位向信号重建在多帧超分辨理论中,用于重建的低分辨率图像间存在相似但不一致的信息,超分辨处理要利用信息中不一致的地方来“生成”还原高分辨率图像需要的信息。如何利用这些不一致信息,超分辨理论中有很多不同的方法,本节从超分辨率处理的角度出发,利用各通道相似但不一致的信息重建等效单通道信号原型。
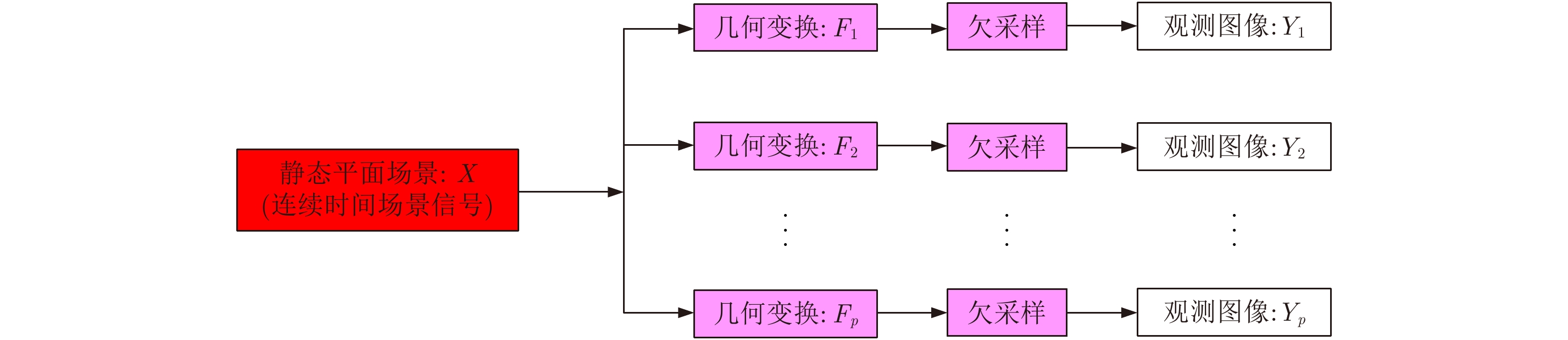
多帧超分辨处理首先须假设一个图像退化模型,这个模型是联系各幅低分辨率图像与最终获取高分辨率图像的纽带。其次,此模型须在某种方式上可逆,从而可以从求逆中得到高分辨率图像。一种简单的图像退化模型如图5所示,即时间连续的场景经几何变换(如旋转、平移等)后采样得到低分辨率的场景图像,采样率小于奈圭斯特采样率。超分辨处理就是将建立的图像(信号)退化模型经过某种描述后进行逆推,从而还原原来的高分辨率图像(高采样率信号)。
|
图 5 仅考虑几何变换的图像退化模型 Fig.5 Image degradation model with only geometric transformation considered |
在图3中,方位向连续时间信号
|
${s_k}\left( i \right) = s\left( {\frac{i}{{{\rm{PRF}}}} + \frac{{\Delta {x_k}}}{{2v}}} \right)$
|
(5) |
|
${S_k}\left( \omega \right) = S\left( \omega \right) \cdot \exp \left\{ {{\rm{j}}\omega \frac{{\Delta {x_k}}}{{2v}}} \right\}$
|
(6) |
|
${S_{kn}} \!=\! \sum\limits_{i = 0}^{N - 1} {{s_k}\left( i \right) \!\cdot\! \exp\! \left\{ { \!- {\rm{j}}2{π} \frac{{in}}{N}} \right\}} ,\begin{array}{*{20}{c}}{}& \!\!\!\!\!\!\! {n = 0, ·\!·\!· ,N \!\! - \!\! 1}\end{array}$
|
(7) |
根据CFT与DFT的关系[22],
|
${S_{kn}} = \frac{1}{T}\sum\limits_{m = - \infty }^{ + \infty } {{S_k}\left( {\frac{n}{{NT}} + m \cdot {\rm{PRF}}} \right)} $
|
(8) |
式(8)是对各通道欠采样信号的频域描述,其中
|
$\begin{aligned}{S_{kn}} = & \frac{1}{T}\sum\limits_{m = - \infty }^{ + \infty } {S\left( {\frac{n}{{NT}} + m \cdot {\rm{PRF}}} \right)} \\{}&{ \cdot \exp \left\{ {{\rm{j}}2{π} \frac{{\Delta {x{_k}}}}{{2v}}\left( {\frac{n}{{NT}} + m \cdot {\rm{PRF}}} \right)} \right\}}\end{aligned}$
|
(9) |
式中,
|
$\begin{aligned}{S_{kn}} =& \frac{1}{T}\sum\limits_{i = 1}^{2L} {S\left( {\frac{n}{{NT}} + \left( {i - 1 - L} \right) \cdot {\rm{PRF}}} \right)} \\{}&{ \cdot \exp \left\{ {{\rm{j}}2{π} \frac{{\Delta {x_k}}}{{2v}}\left( {\frac{n}{{NT}} + \left( {i - 1 - L} \right) \cdot {\rm{PRF}}} \right)} \right\}}\end{aligned}$
|
(10) |
对于每一个频点n,可得如下矩阵方程:
|
${{{S}}_{kn}} = {\varphi _n}{{{S}}_n}$
|
(11) |
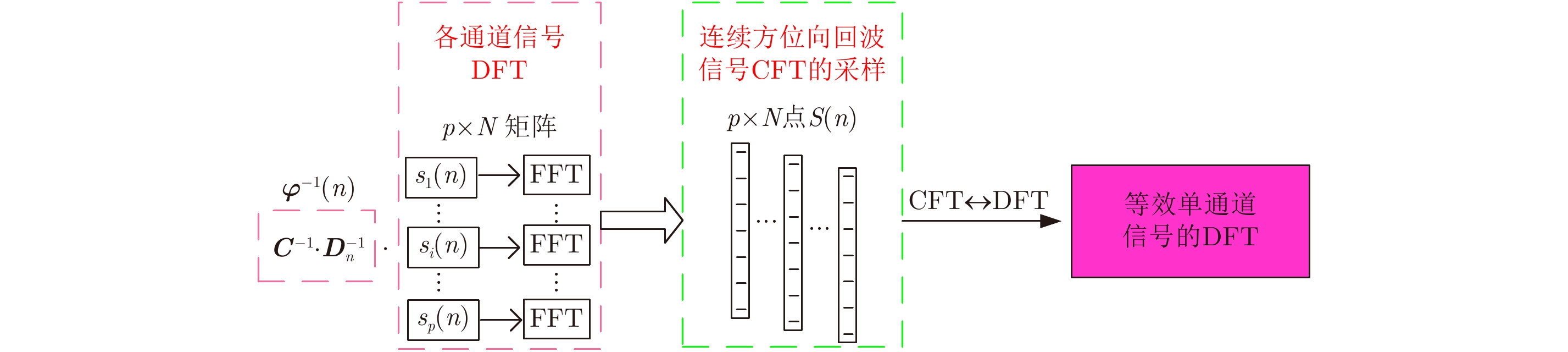
以上对图5图像退化模型的描述是可逆的,这是多帧超分辨处理的基础。图6示意了退化模型的求逆过程:对于每个频点n,式(11)是独立的,
|
图 6 图像(信号)退化模型求逆 Fig.6 Inverse of image (signal) degradation model |
要得到最终结果需解矩阵方程式(11),
|
${{C}} = \left[ {\begin{array}{*{20}{c}}{W_0^0}&{W_0^1}&{W_0^2}& \cdots &{W_0^{2L - 1}}\\{W_1^0}&{W_1^1}&{W_1^2}& \cdots &{W_1^{2L - 1}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\{W_{p - 1}^0}&{W_{p - 1}^1}&{W_{p - 1}^2}& \cdots &{W_{p - 1}^{2L - 1}}\end{array}} \right]$
|
(12) |
C为常量范德蒙德矩阵,如果p=2L,则C为常量范德蒙德方阵。由于C与n无关,故C –1只需计算一次。
Dn可表示为:
|
$\begin{array}{l} \!\!\!\!\! {{{D}}_n} \!=\! {\rm{diag}}\left( {\frac{1}{T} \! \cdot \! \exp \left\{ {{\rm{j}}2{π} \frac{{\Delta {x_0}}}{{2v}}\left( {\frac{n}{{NT}} \!-\! L \cdot \! {\rm{PRF}}} \right)} \right\}} \right. ·\!·· \\\left. {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}\end{array}}& \!\!\!\!\!\!\!\!\!\!\!\!\! { \frac{1}{T} \cdot \exp \! \left\{ {{\rm{j}}2{π} \frac{{\Delta {x_{p - 1}}}}{{2v}}\left( {\frac{n}{{NT}} \!-\! L \cdot {\rm{PRF}}} \right) \!\!} \right\}}\end{array}} \!\!\!\!\! \right)\end{array}$
|
(13) |
对于对角矩阵Dn,可以直接得到其逆矩阵表达式
|
$\begin{align}
& D_{n}^{-1}=\text{diag}\left( T\cdot \exp \left\{ -\text{j}2\pi \frac{\Delta {{x}_{0}}}{2v}\left( \frac{n}{NT}-L\cdot \text{PRF} \right) \right\}\cdots \right. \\
& \left. \ \ \ \ \ \ \ \ T\cdot \exp \left\{ -\text{j}2\pi \frac{\Delta {{x}_{p-1}}}{2v}\left( \frac{n}{NT}-L\cdot \text{PRF} \right) \right\} \right) \\
\end{align}$
|
(14) |
在实际操作中,
|
${{{S}}_n} = {{{C}}^{ - 1}}{{D}}_n^{ - 1}{{{S}}_{kn}}$
|
(15) |
以上在对退化模型的逆推中完成了多帧超分辨处理,多通道信号被合为一路信号,采样率以通道数为倍数增加,即实现信号的均匀化重建。
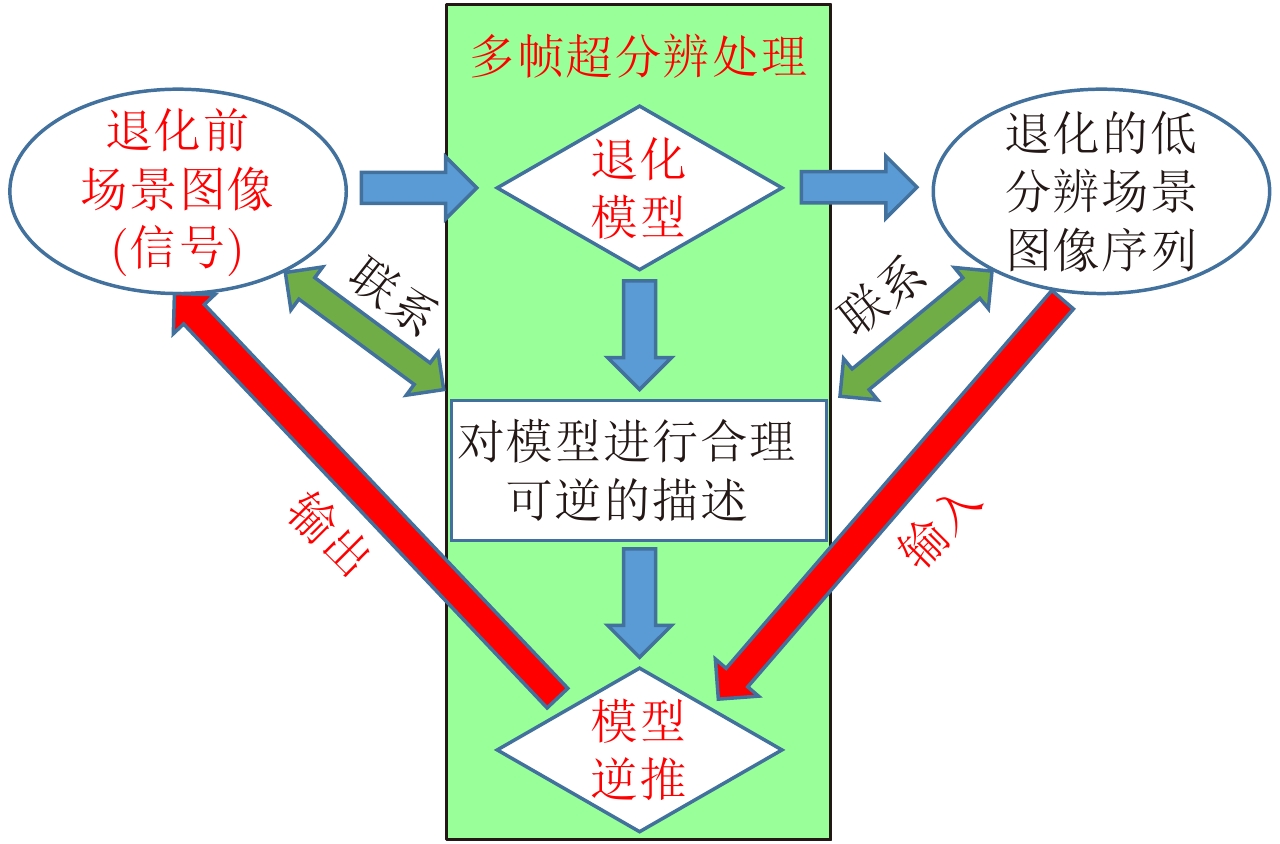
3.3 多帧超分辨处理的一般方法可以总结给出多帧超分辨处理的一般步骤,如图7所示。退化模型联系了原始场景图像与低分辨率图像序列,对模型的描述就是将原始场景图像与低分辨率图像序列之间的联系以可逆的方式表示出来,之后逆推模型即可恢复原始场景图像。应用到方位向多通道系统,在超分辨处理的过程中即实现信号的均匀化重建。
|
图 7 多帧超分辨处理的一般流程 Fig.7 General process for multiframe super-resolution |
需要指出,前面推导的方法不是多帧超分辨方法的全部,退化模型的可逆描述不是唯一的。如文献[18]给出了使用线性方程组直接建立低分辨信号时域采样点与高分辨场景CFT采样的关系,这可以避免对各通道信号进行FFT的操作,但是该方法涉及到大型矩阵的乘法,计算复杂度较高。本文推导的方法原理清晰易懂且计算复杂度低,作为对本文思路验证的示范性方法是合适的。
下一节将给出仿真与实测数据实验结果验证方法的有效性。
4 仿真与实测数据实验本节集中展示方法的星载系统仿真与实测数据实验结果。首先对一星载方位向四通道系统进行仿真,仿真参数如表1所示。
| 表 1 方位向多通道星载SAR系统参数 Tab.1 The parameters for a spaceborne azimuth multichannel system |
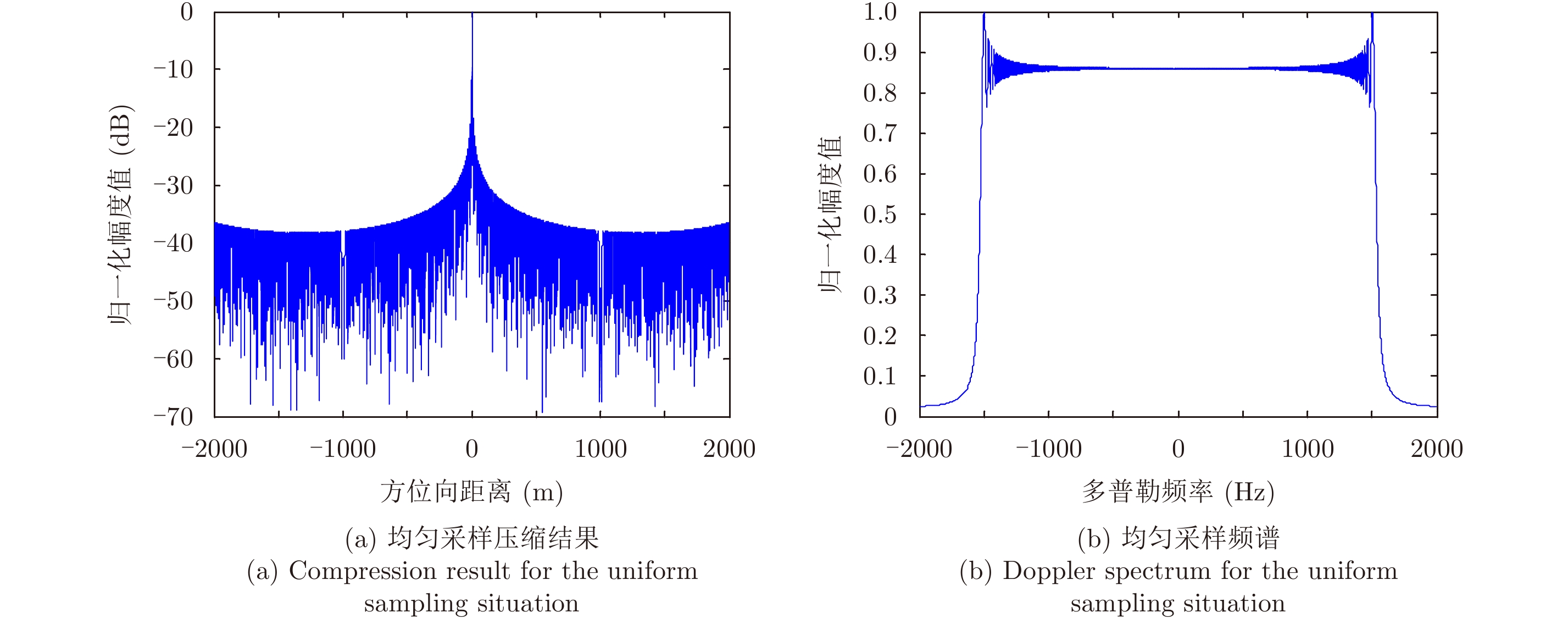
根据式(4),如果
|
图 8 PRF满足均匀采样条件时仿真结果 Fig.8 Simulation results for the uniform sampling situation |
|
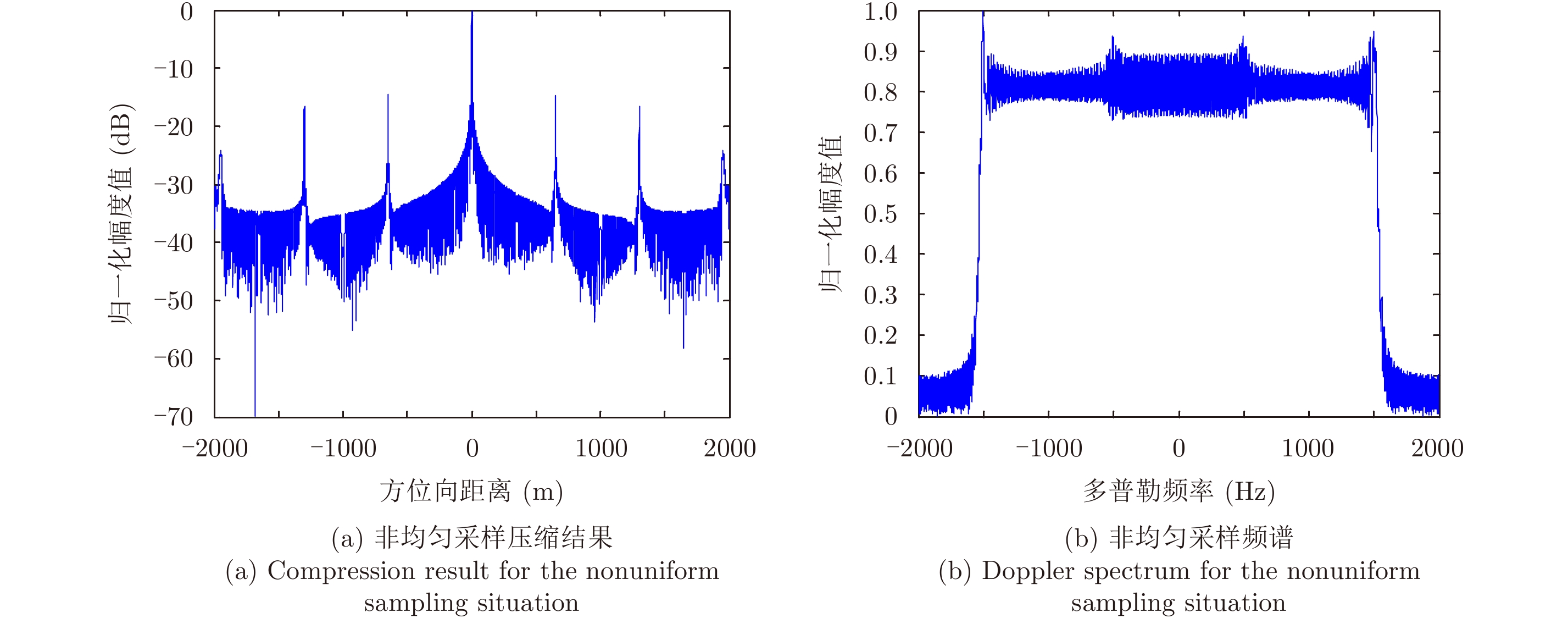
图 9 PRF不满足均匀采样条件时仿真结果 Fig.9 Simulation results for the nonuniform sampling situation |
|
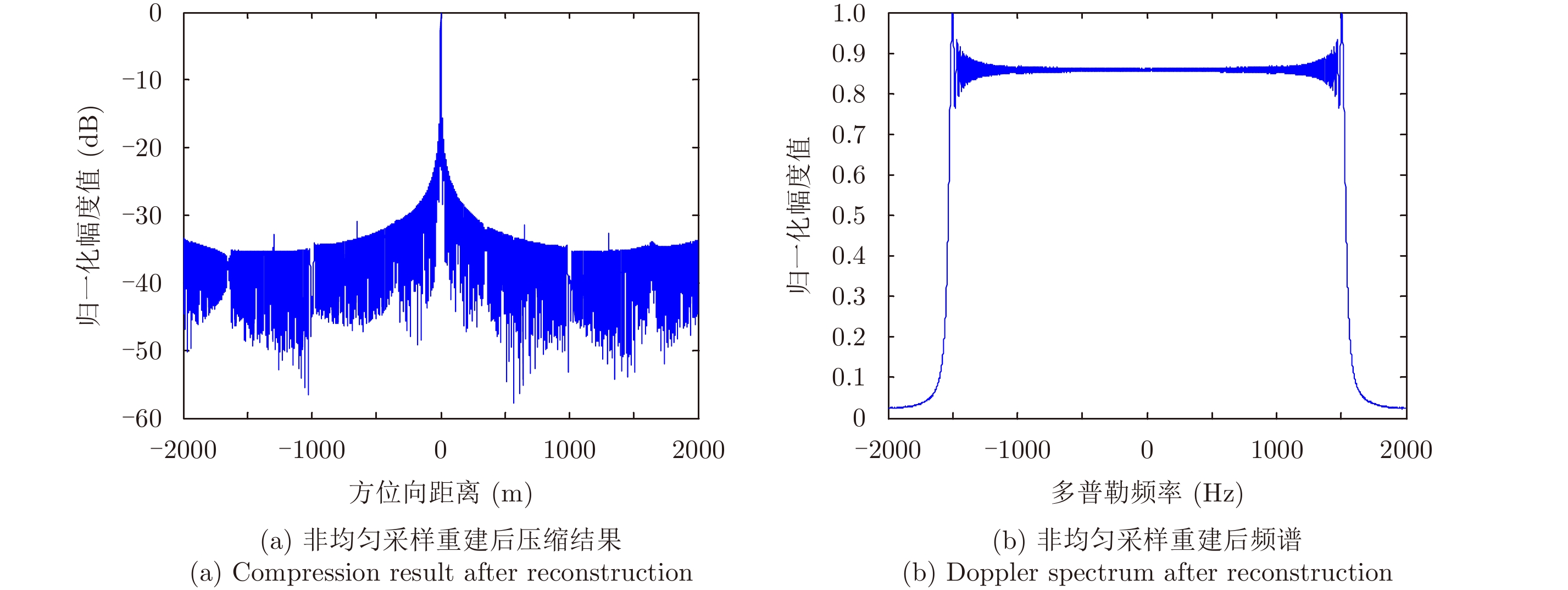
图 10 非均匀采样重建后仿真结果 Fig.10 Simulation results for the nonuniform sampling situation after reconstruction |
|
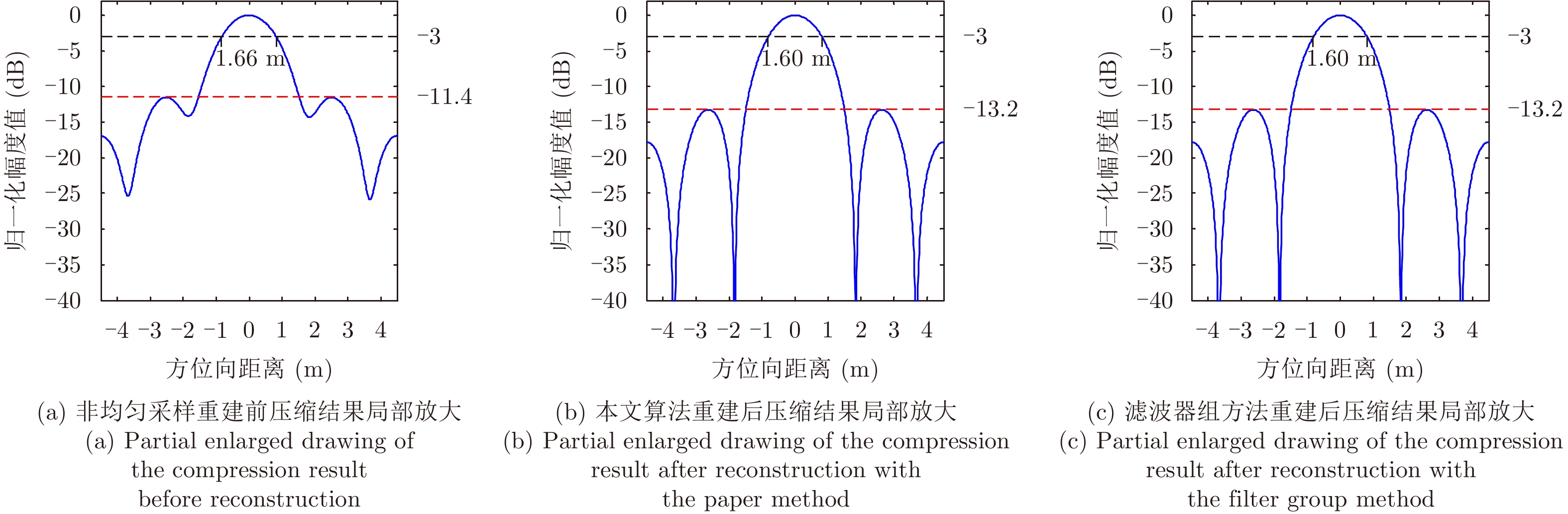
图 11 方位向压缩结果局部放大 Fig.11 Partial enlarged drawing of the compression result in azimuth |
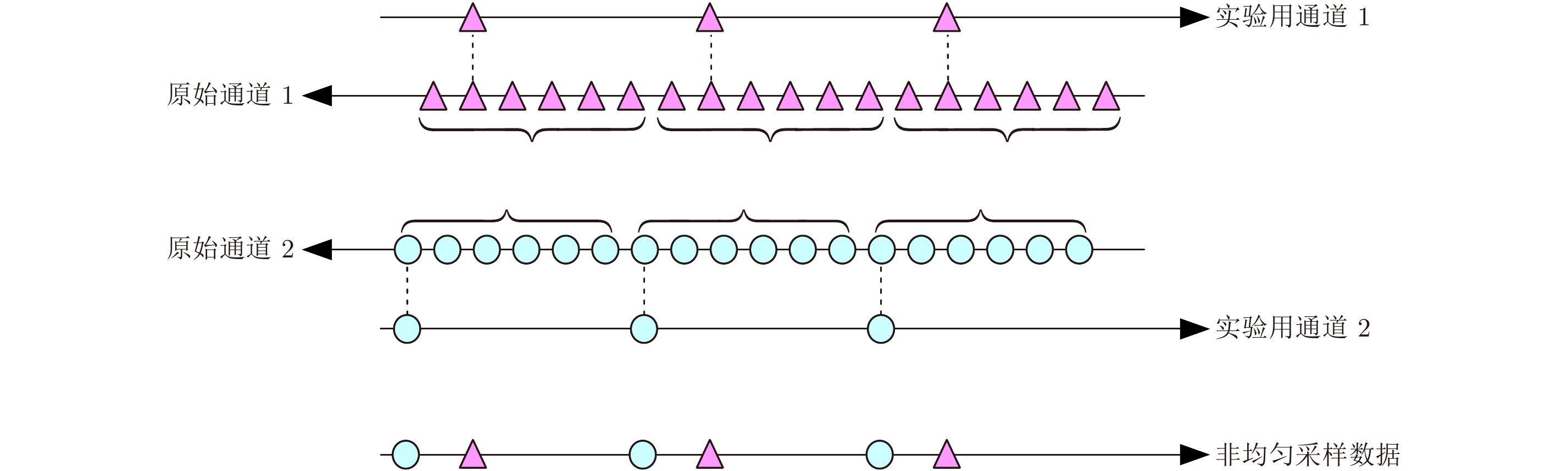
为更好地展示算法性能,我们进行了实测数据实验,所用实测数据由中国科学院电子学研究所收集,为机载方位向双通道系统条带工作模式。由于该机载系统的PRF远大于多普勒带宽(PRF约等于5倍的多普勒带宽),采样率过高使得数据不能直接用于实验,否则难以观察重建效果。我们通过图12的方法使每通道数据PRF降到原来的1/6,从而使PRF小于多普勒带宽。图13(a)示意了仅使用通道1的数据成像的结果,由于采样率小于多普勒带宽,图中存在明显的模糊。图13(b)是两个通道的方位向非均匀采样数据直接成像的结果,此时等效采样率(
|
图 12 实验用数据获取方法 Fig.12 Acquisition method of the data for experiments |

|
图 13 通道1及两通道不做重建成像结果 Fig.13 The images obtained from the first channel and the unreconstructed nonuniform data |

|
图 14 信号均匀化重建后成像结果 Fig.14 The images obtained after signal reconstruction |
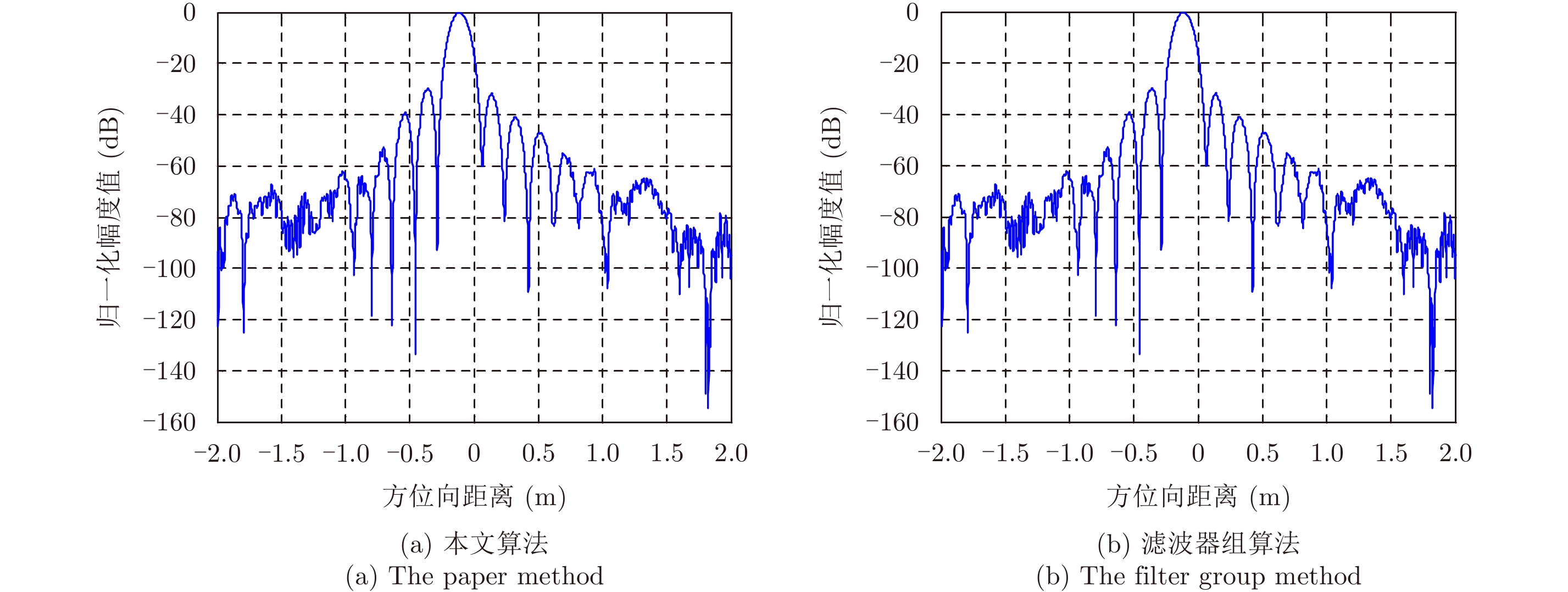
|
图 15 实测数据点目标方位向切片 Fig.15 Zoomed azimuth cut of the point target in the image with both methods |
以上仿真及实测数据实验结果证明了本文方法的有效性,也验证了方位向多通道系统非均匀采样信号重建问题可以看作多帧超分辨率问题进行处理。
5 算法复杂度分析随着计算技术及存储技术的发展,算法的复杂度对算法整体性能的影响在减小,但由于星载SAR的数据是海量的,运算效率的提高及存储需求的降低在海量SAR数据实时处理中仍具有重要的工程实际意义。本节对滤波器组方法及本文方法的复杂度进行分析,本文方法在复杂度性能上具有一定优势。
5.1 滤波器组方法的复杂度基于广义采样定理的滤波器组方法是很多近年来陆续提出方法的基础,本节对其计算复杂度进行分析。文献[9]给出滤波器组方法在工程上一种常见的实现流程并初步计算了运算量,下面分析其总体运算量。假设方位向有p个通道,每通道有N个采样。对各通道回波信号做p倍插值处理,经重建滤波后进行叠加,得到均匀化重建的信号,如图16所示。使用图16中流程处理,则方位向要做p次pN点的FFT及一次pN点的IFFT,另外图中加和处理环节还有
在以上运算流程中,滤波器组方法在方位FFT后数据量以通道数为倍数成倍增加,因此其空间复杂度较高。

|
图 16 滤波器组方法的处理流程 Fig.16 The realization of filter group method |
如前所述,方位向多通道系统信号的非均匀采样重建可以看作类多帧超分辨率问题处理,本文给出了一种基于多帧超分辨率的处理方法,其处理流程如图6所示。
如第3节所述,
另外,在方位向FFT处理后,滤波器组方法所需的原始数据存储空间以通道数为倍数增加,本文方法原始数据存储空间在FFT前后相同。本文方法在时间和空间复杂度性能上具有一定优势。
6 结束语本文在简要介绍图像超分辨率概念的基础上,对方位向多通道系统的信号特性进行了研究,指出了方位向多通道系统的方位向信号特性与多帧超分辨率问题信号特性的联系,对方位向多通道系统非均匀采样信号重建问题与多帧超分辨率问题的相似性进行了证明,第1次指出方位向多通道系统非均匀采样信号重建问题可以看作多帧超分辨率问题。基于此,本文建立了一种简单的图像(信号)退化模型,并根据多帧超分辨处理逆推模型的思路推导了一种非均匀采样信号重建的方法,并总结给出了多帧超分辨处理的一般方法。结合仿真及实测数据实验对方法有效性进行了验证,之后进行了复杂度分析,本文方法在时间与空间复杂度性能上具有一定优势。多帧超分辨率问题是DIP领域的热点,有许多成熟算法可供借鉴,而且多帧超分辨率概念中的有关细节对多通道SAR系统通道误差校正等问题具有指导意义,多帧超分辨率概念在星载SAR多通道技术中具有很好的应用前景,本文思想可为方位向多通道系统非均匀采样信号重建问题的解决提供一种新的思路。
| [1] |
邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J].
雷达学报, 2012, 1(1): 1-10. Deng Yun-kai, Zhao Feng-jun and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1-10. (  0) 0)
|
| [2] |
Lee J S and Pottier E. 洪文, 李洋, 尹嫱, 译. 极化雷达成像基础与应用[M]. 北京: 电子工业出版社, 2013: 199–223.
Lee J S and Pottier E. Hong Wen, Li Yang, and Yin Qiang, Trans. Polarimetric Radar Imaging From Basics to Applications[M]. Beijing: Publishing House of Electronics Industry, 2013: 199–223. (  0) 0)
|
| [3] |
Wiley C A. Synthetic aperture radars[J].
IEEE Transactions on Aerospace and Electronic Systems, 1985, AES-21(3): 440-443. DOI:10.1109/TAES.1985.310578 ( 0) 0)
|
| [4] |
Freeman A, Johnson W T K, Huneycutt B, et al.. The " myth” of the minimum SAR antenna area constraint[J].
IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 320-324. DOI:10.1109/36.823926 ( 0) 0)
|
| [5] |
Currie A and Brown M A. Wide-swath SAR[J].
IEE Proceedings F-Radar and Signal Processing, 1992, 139(2): 122-135. DOI:10.1049/ip-f-2.1992.0016 ( 0) 0)
|
| [6] |
Younis M, Fischer C and Wiesbeck W. Digital beamforming in SAR systems[J].
IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(7): 1735-1739. DOI:10.1109/TGRS.2003.815662 ( 0) 0)
|
| [7] |
Mittermayer J and Runge H. Conceptual studies for exploiting the TerraSAR-X dual receive antenna[C]. Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003: 2140–2142.
( 0) 0)
|
| [8] |
Krieger G, Gebert N and Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J].
IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 260-264. DOI:10.1109/LGRS.2004.832700 ( 0) 0)
|
| [9] |
齐维孔, 禹卫东. 基于滤波器组的星载SAR DPC-MAB技术方位向非均匀采样信号的重构[J].
系统工程与电子技术, 2008, 30(7): 1218-1222. Qi Wei-kong and Yu Wei-dong. Reconstruction of nonuniform azimuth sampling signals of space borne SAR DPC-MAB technique based on filter banks[J]. Systems Engineering and Electronics, 2008, 30(7): 1218-1222. (  0) 0)
|
| [10] |
Li Zhen-fang, Wang Hong-yang, Su Tao, et al.. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems[J].
IEEE Geoscience and Remote Sensing Letters, 2005, 2(1): 82-86. DOI:10.1109/LGRS.2004.840610 ( 0) 0)
|
| [11] |
陈倩, 邓云凯, 刘亚东, 等. 基于自适应滤波的DPC-MAB SAR方位向信号重建[J].
电子与信息学报, 2012, 34(6): 1331-1336. Chen Qian, Deng Yun-kai, Liu Ya-dong, et al.. SAR azimuth signal reconstruction based on adaptive filtering for the DPC-MAB SAR system[J]. Journal of Electronics & Information Technology, 2012, 34(6): 1331-1336. (  0) 0)
|
| [12] |
Sikaneta I, Gierull C H and Cerutti-Maori D. Optimum signal processing for multichannel SAR: With application to high-resolution wide-swath imaging[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6095-6109. DOI:10.1109/TGRS.2013.2294940 ( 0) 0)
|
| [13] |
Sikaneta I, Cerutti-Maori D, Klare J, et al.. Comparison of multi-channel high-resolution wide-swath SAR processing methods[C]. Proceedings of 2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec, Canada, 2014: 3834–3837.
( 0) 0)
|
| [14] |
Liu Guang-yan, Wang You-lin, and Lin You-quan. Unambiguous reconstruction and imaging of nonuniform sampling SAR signals[C]. Proceedings of the 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 253–256.
( 0) 0)
|
| [15] |
Zhao Shuo, Wang R, Deng Yun-kai, et al.. Modifications on multichannel reconstruction algorithm for SAR processing based on periodic nonuniform sampling theory and nonuniform fast fourier transform[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(11): 4998-5006. DOI:10.1109/JSTARS.2015.2421303 ( 0) 0)
|
| [16] |
Siu W C and Hung K W. Review of image interpolation and super-resolution[C]. Proceedings of 2012 Asia-Pacific Signal & Information Processing Association Annual Summit and Conference, Hollywood, CA, 2012: 1–10.
( 0) 0)
|
| [17] |
苏衡, 周杰, 张志浩. 超分辨率图像重建方法综述[J].
自动化学报, 2013, 39(8): 1202-1213. Su Heng, Zhou Jie and Zhang Zhi-hao. Survey of super-resolution image reconstruction methods[J]. Acta Automatica Sinica, 2013, 39(8): 1202-1213. (  0) 0)
|
| [18] |
刘鹏, 刘定生, 李国庆. 基于矩阵秩估计偏移量的频域超分辨率重建[J].
计算机工程, 2009, 35(15): 29-31, 34. Liu Peng, Liu Ding-sheng and Li Guo-qing. Frequency field super-resolution reconstruction based on estimation offset of matrix rank[J]. Computer Engineering, 2009, 35(15): 29-31, 34. DOI:10.3969/j.issn.1000-3428.2009.15.010 (  0) 0)
|
| [19] |
Jiang Jun-jun, Ma Xiang, Chen Chen, et al.. Single image super-resolution via locally regularized anchored neighborhood regression and nonlocal means[J].
IEEE Transactions on Multimedia, 2017, 19(1): 15-26. DOI:10.1109/TMM.2016.2599145 ( 0) 0)
|
| [20] |
Tsai R Y and Huang T S. Multiframe image restoration and registration[J].
Advances in Computer Vision and Image Processing, 1984, 1(2): 317-339. ( 0) 0)
|
| [21] |
Oppenheim A V, Willsky A S, and Nawab S H. Signals and Systems[M]. Second Edition, Beijing: Publishing House of Electronics Industry, 2015: 190–200.
( 0) 0)
|
| [22] |
Proakis J G and Manolaki D G. 方艳梅, 刘永清, 译. 数字信号处理: 原理、算法与应用[M]. 第4版, 北京: 电子工业出版社, 2014: 332–350.
Proakis J G and Manolaki D G. Fang Yan-mei and Liu Yong-qing, Trans. Digital Signal Processing: Principles, Algorithms, and Applications[M]. Fourth Edition, Beijing: Publishing House of Electronics Industry, 2014: 332–350. (  0) 0)
|




