相控阵雷达能同时发射多个波束,且这些波束能独立的执行检测、跟踪等任务,因此它在多目标跟踪上应用广泛[1]。由于波束的捷变能力,波束在目标上的驻留时间可以通过控制波束的转向进行控制,如果最小化波束在目标上的总驻留时间(即最小化总的跟踪时间),就给波束提供更多的搜索时间,则相控阵雷达便有更多时间完成其他探测任务[2,3]。此外,相控阵雷达采用不规则电子扫描方式,因此它可以在不同方向和不同距离搜索和跟踪目标[4]。基于这些优点,与传统机械扫描雷达相比,相控阵雷达在多目标跟踪方面具有明显优势。然而,雷达的系统资源是有限的,提出合理的资源配置方案来完成多项探测任务是不可或缺的。
多年以来,雷达资源管理一直受到广泛关注,且在这一领域形成了很多优秀的研究。文献[5–7]建立一个使目标满足一定跟踪精度的同时最小化系统资源负载的优化问题,实现了对波束重返和驻留时间的控制,但上述研究都是基于单目标跟踪,且未考虑目标的机动性。在多目标跟踪中,文献[8]给出了一种基于预测协方差来控制雷达波束指向的办法,文献[9]利用分块坐标迭代,实现了多目标跟踪背景下分布式MIMO雷达收发站的联合选择,但这两篇文章只考虑了如何调度波束或传感器节点选择的问题,未研究波束驻留时间的分配。同样基于多目标跟踪,文献[10,11]分析了目标机动性对系统资源的影响,且深入研究了调整波束数量、指向和功率分配等资源分配问题,实现了使最坏目标跟踪性能达到最优的目的,但是该方法主要考虑的是如何使目标性能最优,不涉及资源节约问题。
由于设计限制,相控阵雷达天线产生的波束数量有限,通常小于目标数。理论上,当扫描期间目标被雷达波束照射时,目标将反射一定量的脉冲,且脉冲数量会随着波束驻留时间的延长而增加[12]。如果实现所有回波脉冲的相干积累,即量测信息更加丰富,则目标的跟踪性能将得到有效的提升。不考虑资源分配的固定操作模式虽简单易行,但是如果存在远离雷达、散射截面积(Radar Cross Section, RCS)或过程噪声很强的目标,则无法获得每个目标的最佳跟踪性能。因此,雷达波束根据目标分布,目标RCS和目标机动性来调整驻留时间是至关重要的。
为此,本文提出了一种基于多目标跟踪的相控阵雷达波束和驻留时间联合管理方法,并将该方法转化为一个以总驻留时间为目标函数各目标跟踪精度为约束的优化问题,由于贝叶斯克拉美罗界(Bayesian Cramer-Rao Lower Bound, BCRLB)为目标状态的均方根误差(Mean Squared Error, MSE)提供了一个下界,本文推导了带有资源变量的BCRLB并将它作为本次跟踪的性能准则。在证明了该优化问题的非凸性后本文又提出了一个依次解决波束和驻留时间的两步分解算法。仿真结果证明了本文方法在节约系统资源和保证坏目标跟踪性能上的有效性。
2 系统模型假设某一相控阵雷达位于
| $\varphi _k^q = \left\{ \begin{array}{l}1, \;\;{{目标被波束照射}}\\0,\;\;{{其他}}\end{array} \right.$ | (1) |
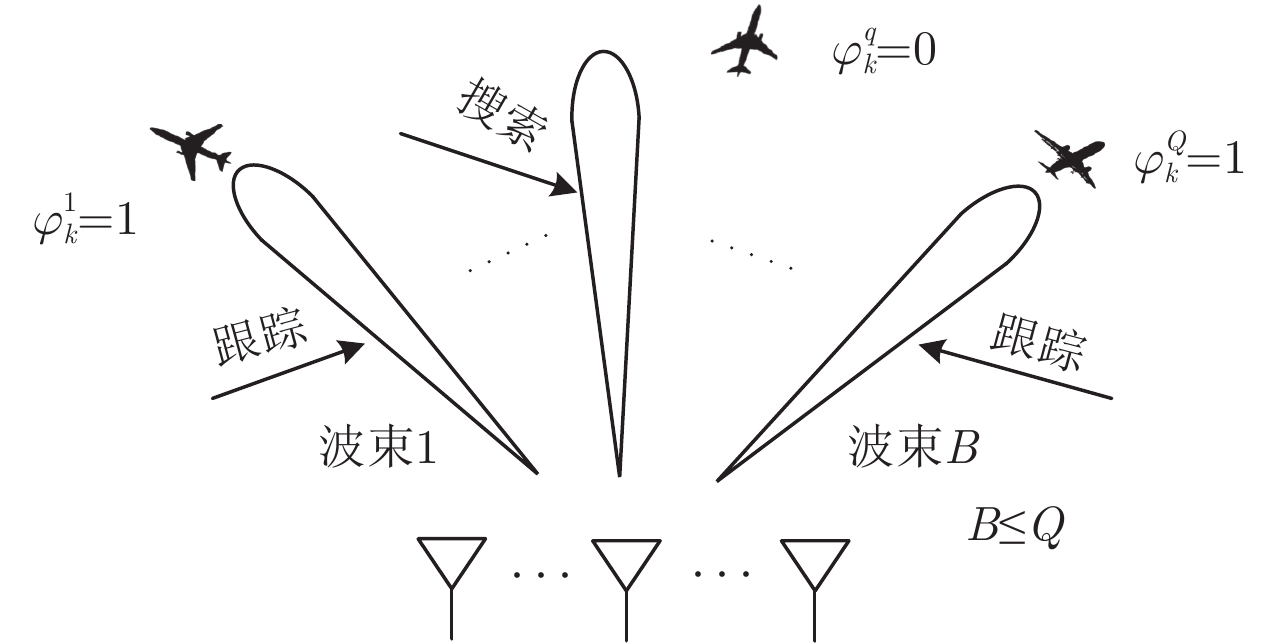
因此,选择哪些目标被波束照射及如何分配波束在目标上的驻留时间是本文将要研究的两个问题。相控阵雷达多波束工作模式示意图如图1所示,雷达波束可独立执行跟踪和搜索任务,当其未照射目标时,认为其在监控区域搜索新的目标。
|
图 1 相控阵雷达多波束工作模式示意图 Fig.1 Multi-beam work mode of phased array radar system |
假设雷达波束发射脉冲信号,脉冲重复周期为Tpri,若k时刻有
| $\begin{aligned}{r_{q,k}}(t,m) = & \sqrt {{E_m}{\alpha _{q,k}}} {h_{q,k}}{s_{\rm{p}}}\left( {t - m{T_{{\rm{pri}}}} - {\tau _{q,k}}} \right) \\& \cdot {{\rm{e}}^{ - {\rm j}2{{π}} {f\!_{q,k}}(m)t}} \!+\! {w_{q,k}}(t,m),\;m \!=\! 1, ·\!·\!· ,{M_{q,k}}\end{aligned}$ | (2) |
其中,
| $\begin{aligned}{S_{q,k}}(t,f) = & {\rm{DFT}}[{r_{q,k}}(t,m)]\\ = & \sum\limits_{m = 0}^{{M_{q,k}} - 1} {{r_{q,k}}(t,m){{\rm{e}}^{ - {\rm j}2{{π}} fm{T_{{\rm{pri}}}}}}} \end{aligned}$ | (3) |
理论上,当
| $\begin{aligned}{\rm{SN}}{{\rm{R}}_{q,k}}(\Delta {T_{q,k}}) & = \frac{{{{\left| {{M_{q,k}}\sqrt {{E_m}{\alpha _{q,k}}} {h_{q,k}}} \right|}^2}}}{{{M_{q,k}}\sigma _w^2}}\\& = \frac{{{P_{{\rm{av}}}}\Delta {T_{q,k}}{\alpha _{q,k}}{{\left| {{h_{q,k}}} \right|}^2}}}{{\sigma _w^2}}\end{aligned}$ | (4) |
从上式可以看出,回波信噪比
目标作匀速运动,目标q在k时刻的状态为:
| ${{x}}_k^q = {{{F}}\!_k}{{x}}_{k - 1}^q + {{u}}_{k - 1}^q$ | (5) |
其中,Fk表示状态转移矩阵,过程噪声
| ${{{F}}\!_k} = {{{I}}_2} \otimes \left[ {\begin{array}{*{20}{c}}1 & {{T^{\rm{ \! s}}}}\\0 & 1\end{array}} \right]\quad\quad\quad\quad\quad\quad\quad\,\,$ | (6) |
| ${{{Q}}_{q,k - 1}} = {\kappa _q}{{{I}}_2} \otimes \left[ {\begin{array}{*{20}{c}}{{{({T^{\rm{ \! s}}})}^3}/3} & {{{({T^{\rm{ \! s}}})}^2}/2}\\{{{({T^{\rm{ \! s}}})}^2}/2} & {{T^{\rm{ \! s}}}}\end{array}} \right]$ | (7) |
其中,I2为2阶单位矩阵,
从回波信号中提取距离和角度信息,在k时刻,目标量测方程可表示为:
| ${{{z}}_{q,k}} = {{{g}}_{q,k}}({{x}}_k^q) + {{{v}}_{q,k}}$ | (8) |
其中,每个目标来自雷达的量测,即距离和角度,分别为:
| ${{{g}}_{q,k}}({{x}}_k^q) = \left[ \begin{array}{l}{R_{q,k}}\\\, {\theta _{q,k}}\end{array} \right] = \left[ \begin{array}{l}\sqrt {{{(x_k^q - x)}^2} + {{(y_k^q - y)}^2}} \\\quad\ \arctan \left[ {\frac{{y_k^q - y}}{{x_k^q - x}}} \right]\end{array} \right]$ | (9) |
| $\begin{array}{l}{{{G}}_{q,k}}(\Delta {T_{q,k}}) = \left[\!\!\!\! \begin{array}{l}\begin{array}{*{20}{c}}{\sigma _{{R_{q,k}}}^2} & \ \ 0\end{array}\\\begin{array}{*{20}{c}}\ \ 0 & \ \ {\sigma _{{\theta _{q,k}}}^2}\end{array}\end{array} \!\!\!\!\right]\\ \propto \left[\!\!\!\! \begin{array}{l}\begin{array}{*{20}{c}}\!\!{{{({\rm{SN}}{{\rm{R}}_{q,k}}(\Delta {T_{q,k}})\beta _{q,k}^2)}^{ - 1}}} &\quad\quad\quad \ 0\end{array}\\\begin{array}{*{20}{c}}\quad \quad\quad\quad 0 & \quad\quad\quad \ {{{({\rm{SN}}{{\rm{R}}_{q,k}}(\Delta {T_{q,k}})/{W_{{\rm{NN}}}})}^{ - 1}}}\!\!\end{array}\end{array} \!\!\!\!\right]\end{array}$ | (10) |
其中,
在本节中,该文将波束指向和驻留时间联合分配问题转化为一个以总驻留时间为目标函数,波束、驻留时间和跟踪性能为约束的优化问题。目标动态模型和量测模型的不准确性可能导致目标状态估计的不确定性。然而BCRLB综合了目标分布、目标RCS、过程噪声和驻留时间等变量,也为这些变量参数无偏估计的MSE提供了一个下界[16–19],所以,将它作为跟踪性能的准则是合理且可行的。基于此,本节推导了带有波束和驻留时间变量的BCRLB,并将跟踪精度误差的下界提取出来,在跟踪时刻k,当k–1时刻的贝叶斯Fisher信息矩阵(Bayesian Fisher Information Matrix, BFIM)已知,给定一组波束变量
假设目标估计状态为
| $\begin{aligned}& {{\mathbb{E}}_{ {x}_k^q,{ {z}_{q,k}}}}\{ ({\hat{ {x}}}_k^q({{{z}}_{q,k}}) - {{x}}_k^q){({\hat{ {x}}}_k^q({ {z}_{q,k}}) - {{x}}_k^q)^{\rm{T}}}\} \\& \quad \quad \quad \ge {{C}}({{x}}_k^q) = {{{J}}^{ - 1}}({{x}}_k^q)\end{aligned}$ | (11) |
其中,
| ${{J}}({{x}}_k^q) = {{{J}}_{\rm{P}}}({{x}}_k^q) + {{{J}}_{\rm{D}}}({{x}}_k^q)$ | (12) |
| $\left\{\!\! \begin{aligned}{{{J}}_{\rm{P}}}({{x}}_k^q) = \left[{({{{Q}}_{q,k - 1}} + {{{F}}_k}{{{J}}^{ - 1}}({{x}}_{k - 1}^q)({{{F}}_k})^{\rm{T}}}\right]^{ - 1}\\{{{J}}_{\rm{D}}}({{x}}_k^q) = {{\mathbb{E}}_{ {x}_k^q}}\left\{ {{{{H}}^{\rm{T}}}({{x}}_k^q){{G}}_{q,k}^{ - 1} (\Delta {T_{q,k}}){{H}}({{x}}_k^q)} \right\}\end{aligned} \right.$ | (13) |
其中,
在k时刻,对于目标q,它可能不被波束照射,此种情况下,驻留时间为零且目标数据FIM不存在,代入波束变量
| $\begin{aligned}{{J}}(\varphi _k^q,\Delta {T_{q,k}}){|_{{x}_k^q}} = & {{{J}}_{\rm{P}}}({{x}}_k^q) +\varphi _k^q{{\mathbb{E}}_{{x}_k^q}}\left\{\! {{{H}}^{\rm{T}}}({{x}}_k^q)\right. \\& \cdot \left. {{G}}_{q,k}^{ - 1} (\Delta \! {T_{q,k}}){{H}}({{x}}_k^q) \!\right\}\end{aligned}$ | (14) |
对上式求逆,求得预测BCRLB为:
| ${{C}}(\varphi _k^q,\Delta {T_{q,k}}){|_{{x}_k^q}} = {[{{J}}(\varphi _k^q,\Delta {T_{q,k}}){|_{{x}_k^q}}]^{ - 1}}$ | (15) |
由式(11)可知,目标BCRLB的对角线上元素不仅可以反映目标位置估计方差的下界,还可以反映速度分量估计误差的下界,所以将BCRLB直接作为跟踪精度误差的准则是不准确的,需将跟踪精度误差提取出来:
| $L(\varphi _k^q,\Delta {T_{q,k}}) = \sqrt {{{C}}(1,1) + {{C}}(3,3)} $ | (16) |
其中,C(1, 1)和C(3, 3)分别表示BCRLB对角线上的第1个和第3个分量,因此
本方法的目的是在保证所有目标满足一定跟踪精度
| $\begin{array}{l}\min \;\;\;\;{1}_Q^{\rm{T}}\Delta {{{T}}_k}\\{\rm s.t.}\;\;\left\{ \begin{array}{l}\varphi _k^q = \left\{ {0,1} \right\} , \; q = 1,2, \cdots ,Q\\{1}_Q^{\rm{T}}{φ_k} = B\,'\!\!_k \le B\\\Delta {T_{\min }} \le \Delta {T_{q,k}} \le \Delta {T_{\max }} , \; \varphi _k^q = 1\\\Delta {T_{q,k}} = 0 , \; \varphi _k^q = 0\\{1}_Q^{\rm{T}}\Delta {{{T}}_k} \le {T_{{\rm{track}}}}\\ L(\varphi _k^q,\Delta {T_{q,k}}) \le \eta \end{array} \right.\end{array}$ | (17) |
其中,
对于一个优化问题,首先需要判断它的凸性。通过判定可知,
实际上,分配波束就是选择哪些目标被照射,从目标BFIM的组成部分可知,先验FIM
(1) 根据k时刻每个目标的先验信息矩阵
(2) 令
(3) 将
| $φ_k^{{\rm{opt}}}(q) = \left\{ \begin{array}{l}1,\;{{如果}}\;{L^{\rm{P}}}({{x}}_k^q) \ge \eta \\0,\;{{如果}}\;{L^{\rm{P}}}({{x}}_k^q) < \eta \end{array} \right.$ | (18) |
上式说明,k时刻,若目标的预测跟踪精度已满足跟踪要求
(4) 计算出通过此法得到的用于跟踪的总波束数量
| ${{L}}_k^{\rm{P}} = {\left[{L^{\rm{P}}}\left({{x}}_k^1\right),{L^{\rm{P}}}\left({{x}}_k^2\right), \cdots ,{L^{\rm{P}}}\left({{x}}_k^Q\right)\right]^{\rm{T}}}$ | (19) |
然后将它们按照从大到少的方式排列,得
| $[{{L}}_{k,{\rm{sort}}}^{\rm{P}},{\bf{o}}] = {\rm{sort}}[{{L}}_k^{\rm{P}},{\rm{descend}}]$ | (20) |
因为目标预测跟踪精度准则的值越大,说明目标的先验FIM越差,则这个目标就更需要来自于雷达的观测信息进行状态更新,所以当
| $\hat{φ}_k^{{\rm{opt}}}(q) = \left\{ \begin{array}{l}1, \;{{如果}}\;q \in {\bf{o}}(1:M)\\0,\;{{如果}}\;q \in {\bf{o}}(M + 1:Q)\end{array} \right.$ | (21) |
由于波束资源总数有限,通过这种方式得到的波束选择结果虽然可能会使k时刻有
| $L({{x}}_k^q) \!=\! \left\{\!\!\!\! \begin{array}{l}\sqrt {{{C}}(1,1) + {{C}}(3,3)} , \;\quad \hat{φ}_k^{{\rm{opt}}}(q) = 1\\\sqrt {{{{C}}^{\rm{P}}}(1,1) + {{{C}}^{\rm{P}}}(3,3)} , \; \hat{φ}_k^{{\rm{opt}}}(q) = 0\end{array} \right.$ | (22) |
基于以上得到的波束分配结果
| $\begin{array}{l}\mathop {\min }\limits_{\Delta {{T}_k}} \;\;\;{1}_Q^{\rm{T}}\Delta {{{T}}_k}\\{\rm s.t.}\;\;\;\left\{ \begin{array}{l}\Delta {T_{\min }} \le \Delta {T_{q,k}} \le \Delta {T_{\max }},\;\hat{φ}_k^{{\rm{opt}}}(q) = 1 \\{1}_Q^{\rm{T}}\Delta {{{T}}_k} \le {T_{{\rm{track}}}}\\L(\Delta {T_{q,k}}) \le \eta \end{array} \right.\end{array}$ | (23) |
由文献[10,20]可知,若BFIM的初始值是半正定的,则
由于观测模型是非线性的,本文采用粒子滤波算法来实现对目标的状态估计[22,23]。在k时刻,如果目标q被波束照射(
| $p({{x}}_k^q\left| {{{{z}}_{q,1:k}}} \right.) \propto p({{{z}}_{q,k}}\left| {{{x}}_k^q} \right.)p({{x}}_k^q\left| {{{{z}}_{q,1:k - 1}}} \right.)$ | (24) |
其中
| $p({{{z}}_{q,k}}\left| {{{x}}_k^q} \right.) = {\cal N}({{{g}}_{q,k}}({{x}}_k^q),{{{G}}_{q,k}}(\Delta {T_{q,k}}))$ | (25) |
如果目标未被照射(
通过仿真,本文对波束和驻留时间联合分配策略进行评估。由于脉冲数目是对驻留时间更直观的显示,在以下的仿真中本文将用脉冲数目来反应驻留时间,本文提出方法脉冲数目的计算表达式为
| ${\rm{RMS}}{{\rm{E}}_{q,k}} \!=\! \sqrt {\frac{1}{{{N_{{\rm{mc}}}}}}\sum\limits_{j = 1}^{{N_{{\rm{mc}}}}} {\left[ {{{\left( {x_k^q - \hat x_k^{q,j}} \right)}^2} + {{\left( {y_k^q - \hat y_k^{q,j}} \right)}^2}} \right]} } $ | (26) |
其中,Nmc为蒙特卡洛次数,
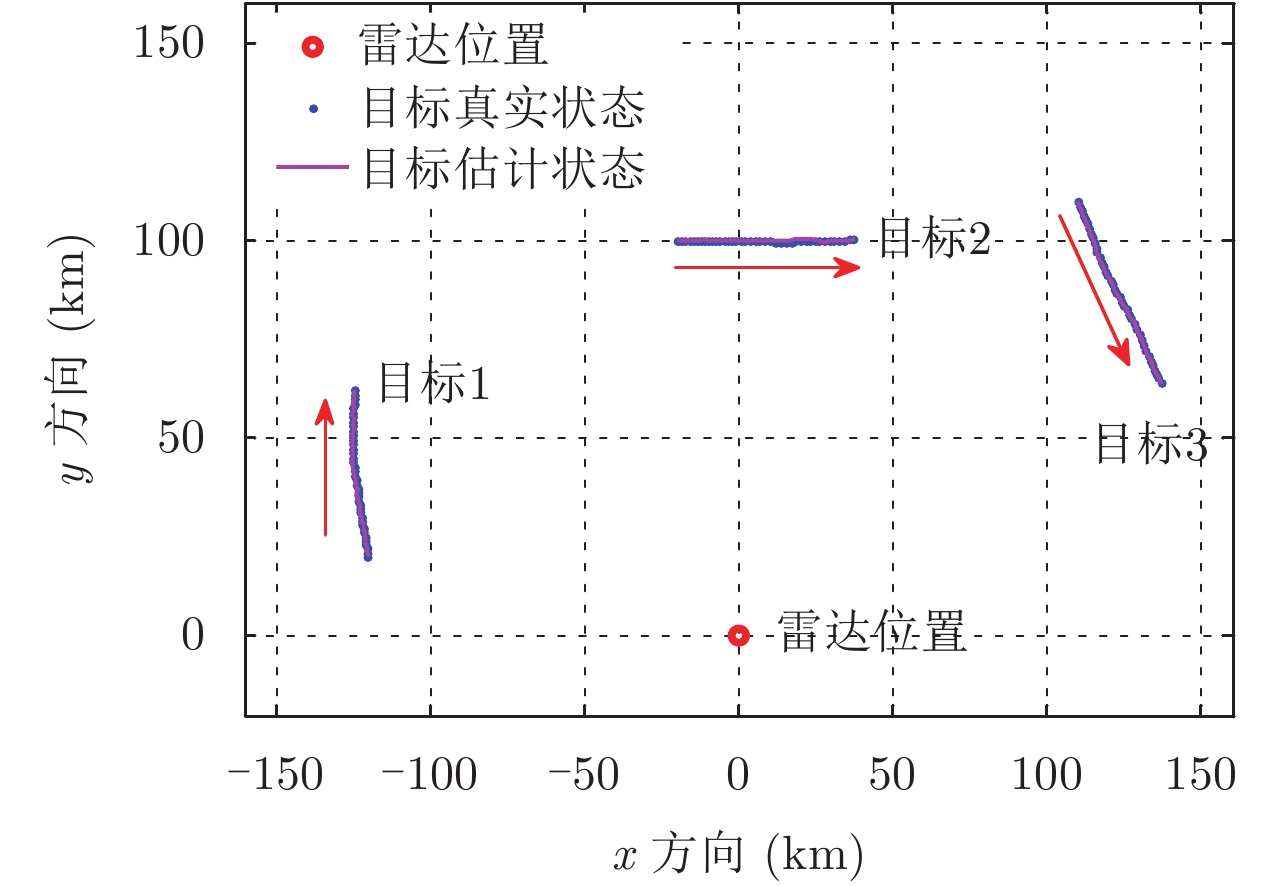
假设雷达的初始位置为(0, 0),目标的初始状态和距离雷达的初始距离如表1所示。目标的航迹和其相对于雷达位置的分布如图2。为了更好地反映目标分布对资源的影响,本次仿真设置每个目标到雷达的初始距离是有一定差别的。另外,考虑到目标RCS和过程噪声对资源分布的影响,本文分别设置了两种RCS模型
(1)
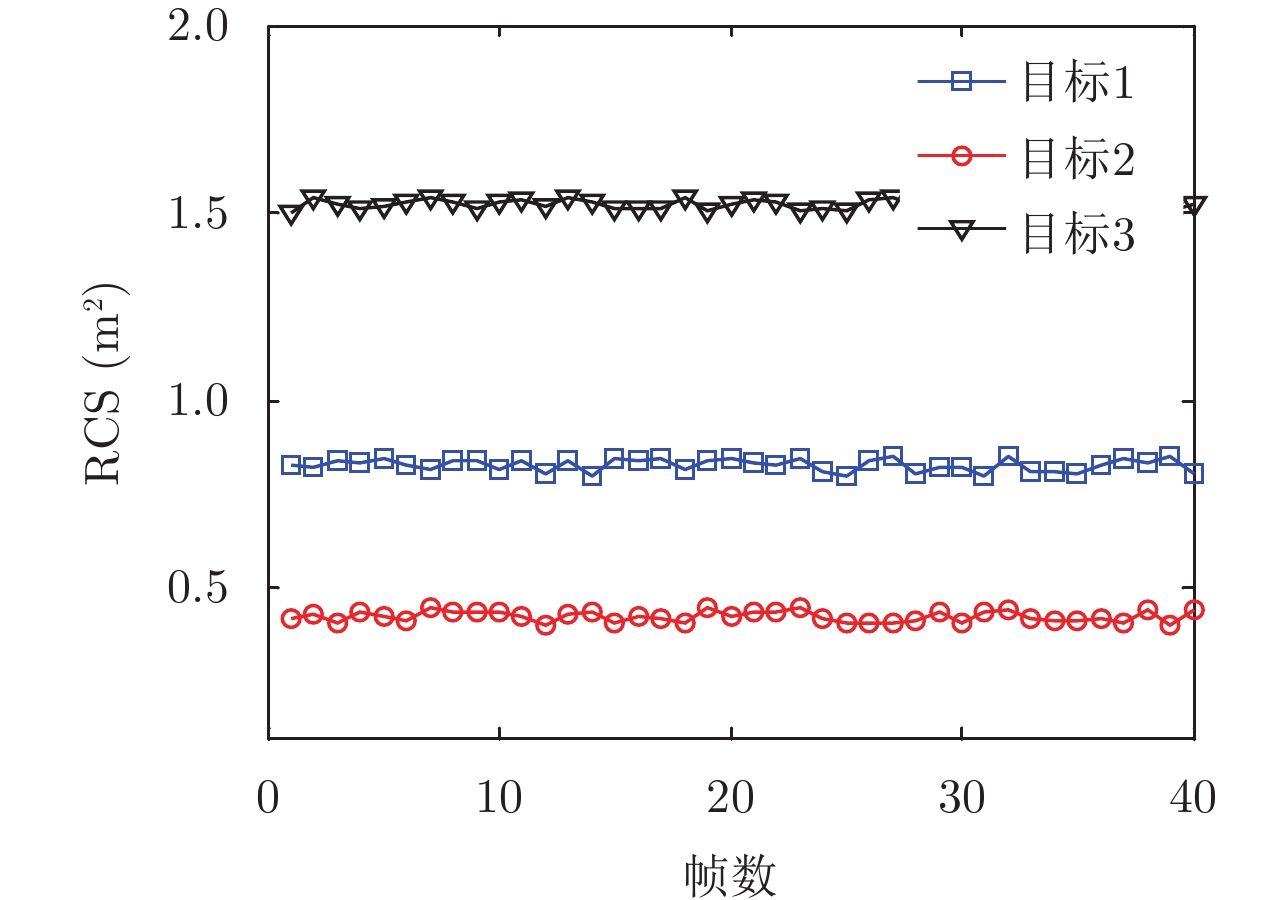
(2) H2:如图3所示
和两种过程噪声模型
(1)
(2)
结合目标分布、目标RCS和过程噪声,本文将分析以下3种情况下资源的分配结果。
| 表 1 目标初始状态及距离雷达距离 Tab.1 Initial target state and distance from each target to radar |
|
图 2 目标航迹与雷达位置分布图 Fig.2 Deployment of targets with respect to radar |
|
图 3 第2种目标RCS模型图 Fig.3 Second target RCS models |
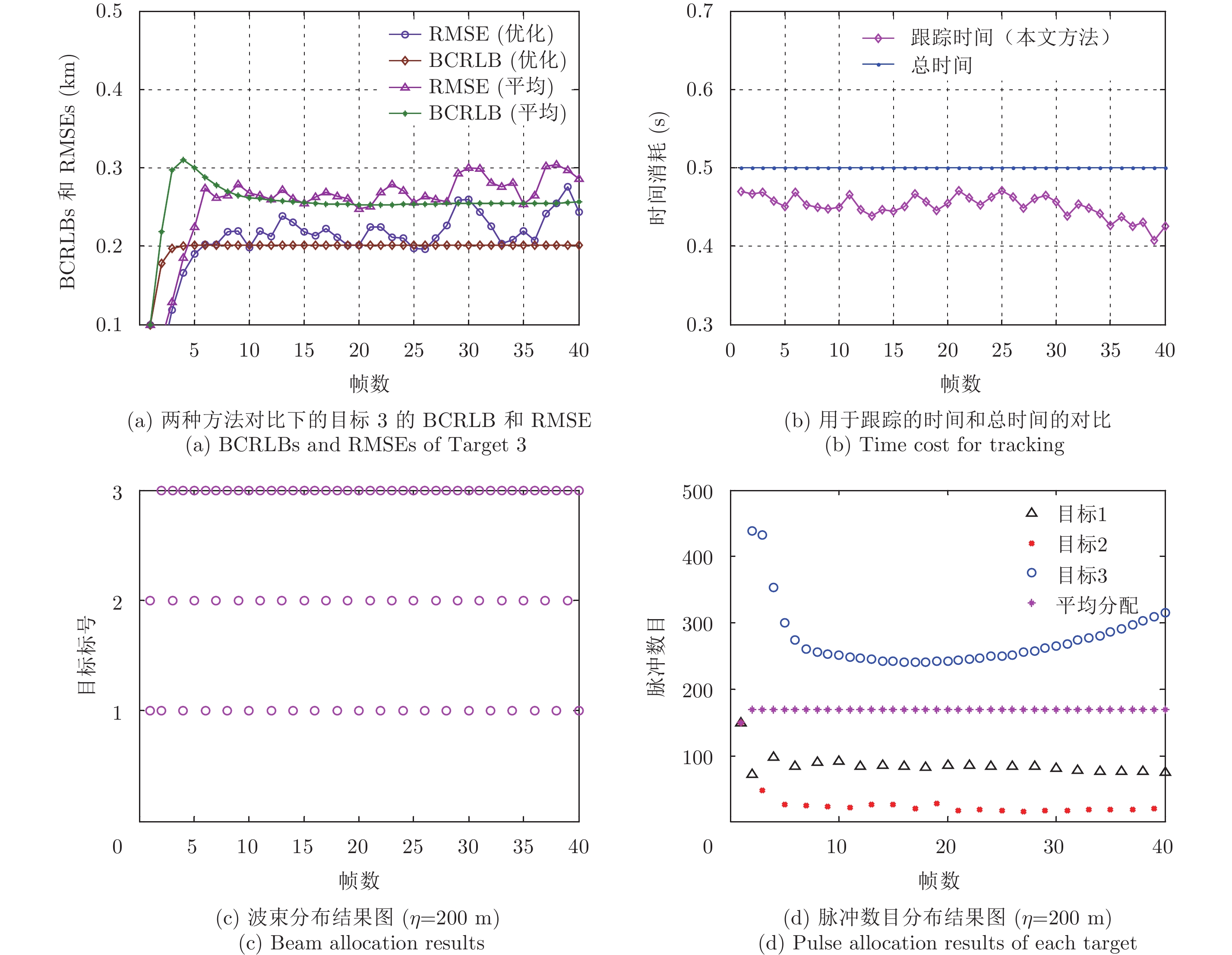
此种场景仿真中,假设所有目标的RCS和过程噪声强度都一样,即未考虑目标RCS和过程噪声对资源分配的影响,所以资源分配只跟目标到雷达的距离有关。图4(a)为本文方法和平均分配资源方法下目标3的BCRLB和RMSE对比图。可以看出,在资源均匀分配的操作模式下,目标3的跟踪精度为250 m,未能达到预定门限
|
图 4 跟踪阈值
|
本场景主要探讨过程噪声对资源分配的影响,波束和脉冲分布结果分别为图5(a)和图5(b)所示。对比图4(c)和图4(d),可以看出,由于目标2的过程噪声变大,机动性变强,虽然它的脉冲数目无明显变化,保持在30左右,但它却被波束一直照射。目标3由于过程噪声的变小,被波束照射的次数减少一半(由40次降到20次),但照射到目标3上的脉冲数依然很多,维持在290,那是因为它离雷达距离最远。可见,波束倾向于将更多资源分配给过程噪声较大和距离雷达较远的目标。这同时也说明,资源分配是多种因素综合作用的结果。
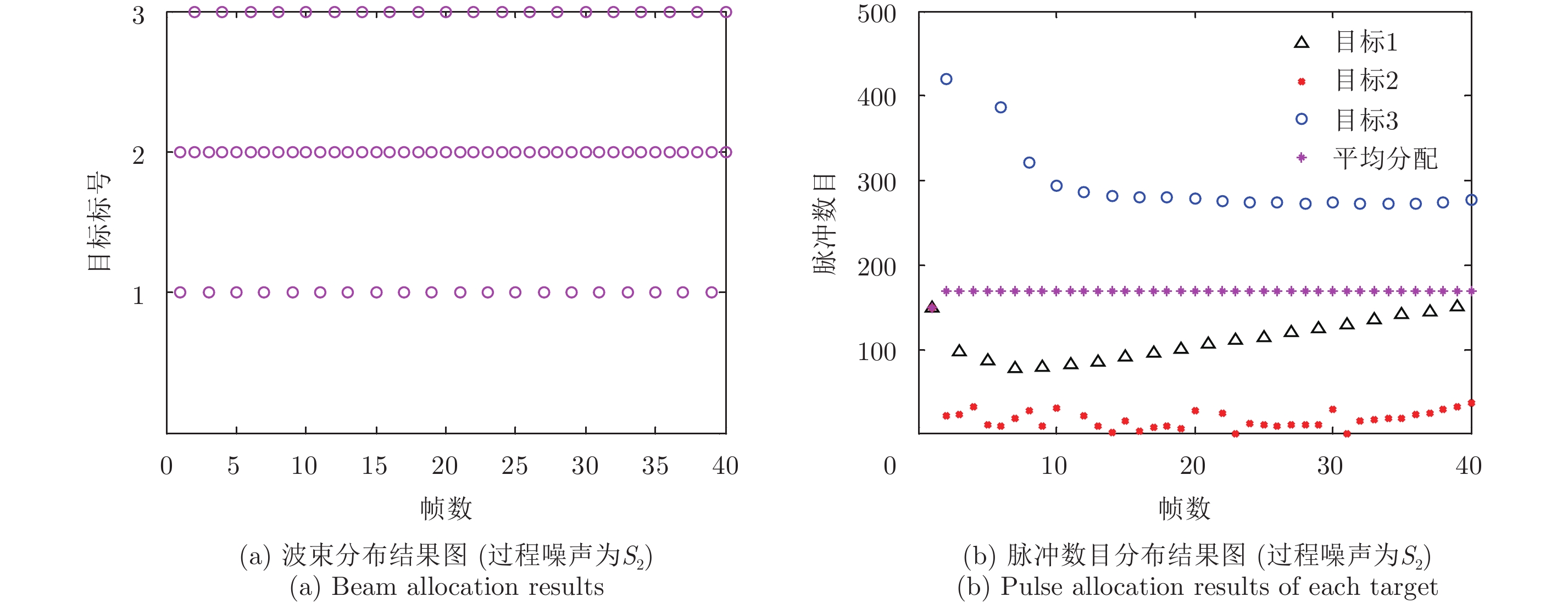
|
图 5 资源分布为H1 and S2时的资源分配 Fig.5 Resources allocation with H1 and S2 |
接着本文探讨了目标RCS模型的变化对资源分配的影响,图6(a)和图6(b)分别为第2种目标RCS模型下,跟踪要求为
图7为分别将跟踪门限设为
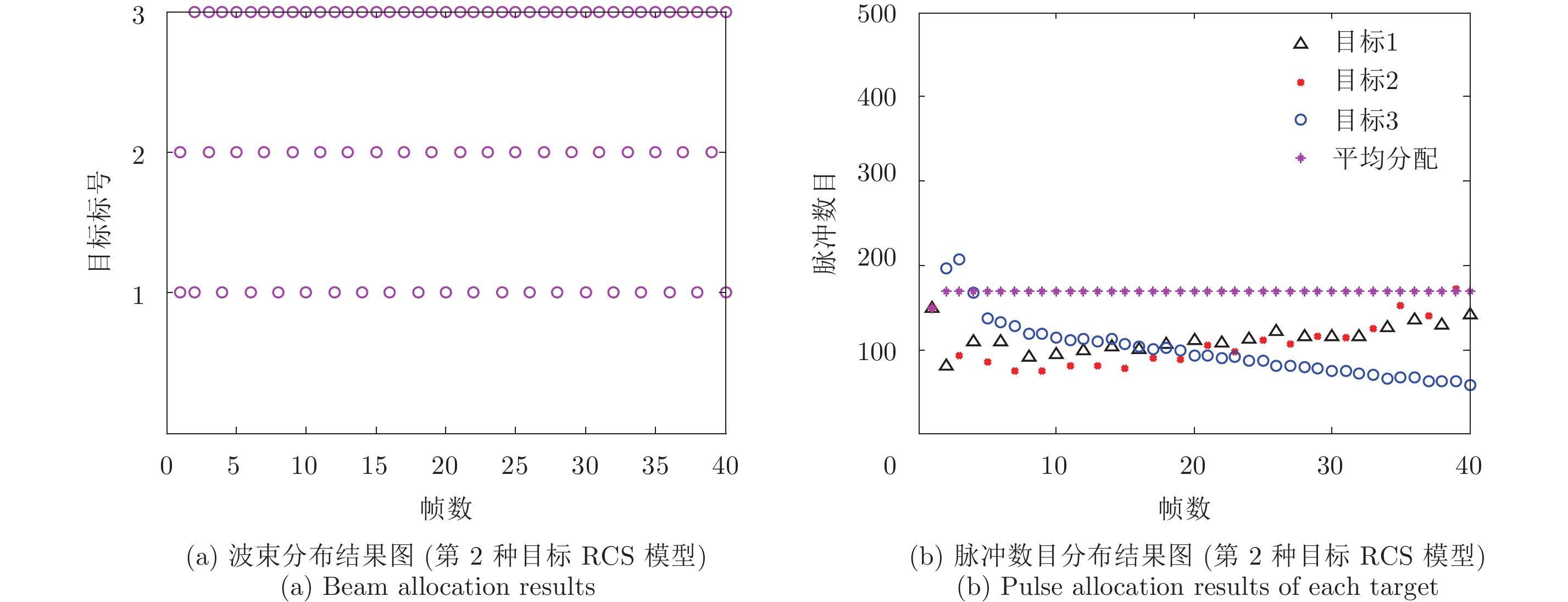
|
图 6 资源分布为H2 and S1时的资源分配 Fig.6 Resources allocation with H2 and S1 |
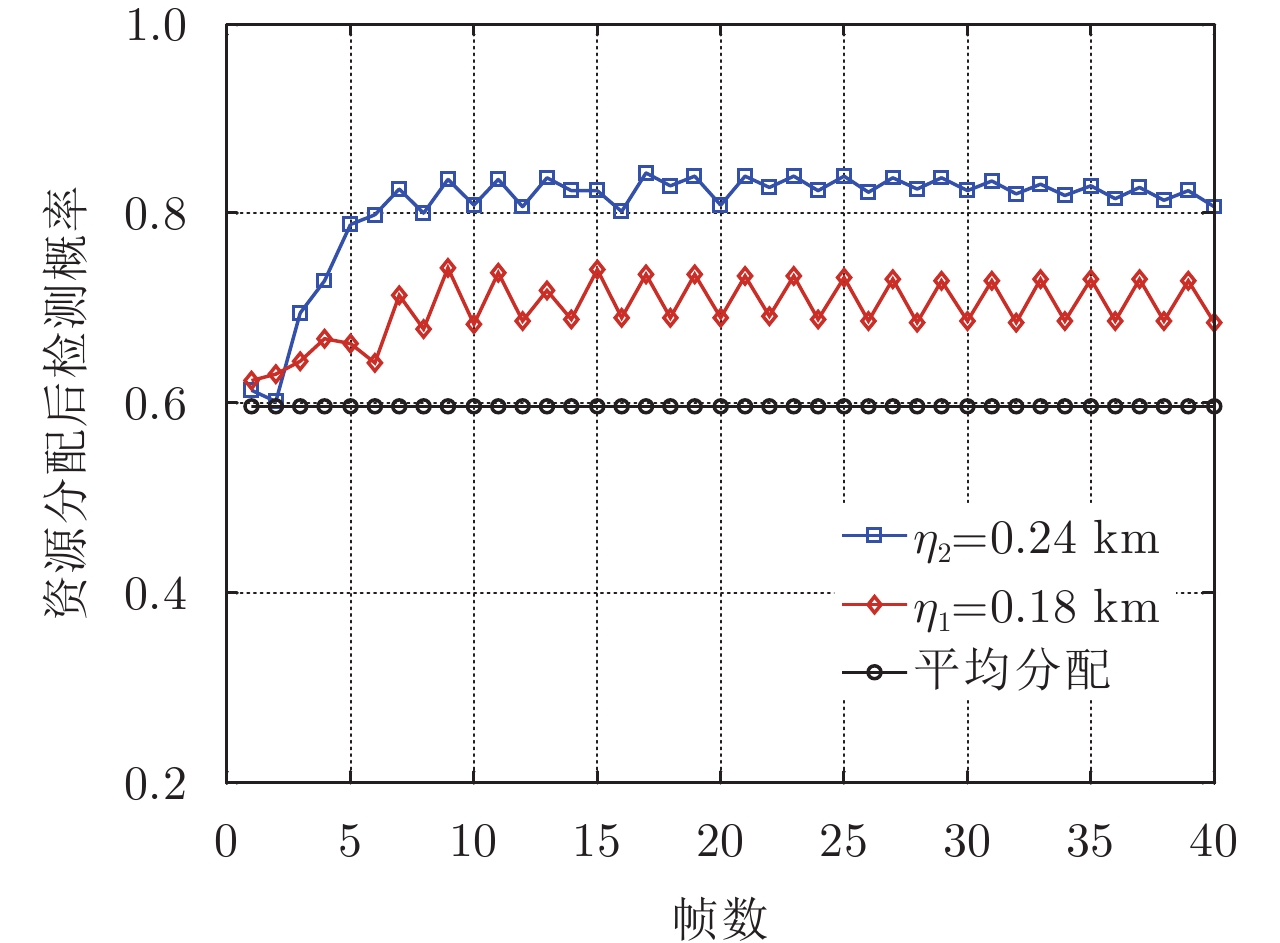
|
图 7 资源分配后检测概率 Fig.7 Detection probability after resource allocation with different tracking thresholds |
本文研究了相控阵雷达的多波束工作模式,提出了一种基于多目标跟踪的波束和驻留时间联合分配方法,旨在用更少的系统资源实现多目标的跟踪。本文推导了带有资源变量的BCRLB并选取它作为跟踪性能准则,然后建立了在保证每个目标的跟踪精度都满足一定要求的前提下,以总驻留时间为目标函数的非凸资源优化问题。随后根据最优化理论提出一个两步分解算法,最后基于资源分配结果,采用粒子滤波实现了多目标跟踪。仿真结果证明本文方法不仅在节约跟踪资源方面效果显著,而且有助于保证远距离目标跟踪性能。
| [1] |
Izquierdo-Fuente A and Casar-Corredera J R. Optimal radar pulse scheduling using a neural network[C]. Proceedings of 1994 IEEE International Conference on Neural Networks, Orlando, Florida, USA, 1994, 7: 4588–4591.
( 0) 0)
|
| [2] |
Kirubarajan T, Bar-Shalom Y, and Daeipour E. Adaptive beam pointing control of a phased array radar in the presence of ECM and false alarms using IMMPDAF[C]. Proceedings of the 1995 American Control Conference, Seattle, WA, USA, 1995, 4: 2616–2620.
( 0) 0)
|
| [3] |
Daeipour E, Bar-Shalom Y, and Li X. Adaptive beam pointing control of a phased array radar using an IMM estimator[C]. Proceedings of 1994 American Control Conference, Baltimore, MD, USA, 1994, 2: 2093–2097.
( 0) 0)
|
| [4] |
何友, 修建娟, 关欣, 等. 雷达数据处理及应用[M]. 第3版, 北京: 电子工业出版社, 2013: 308–313.
He You, Xiu Jian-juan, Guan Xin, et al.. Radar Data Processing with Applications[M]. Third edition, Beijing: Publishing House of Electronics Industry, 2013: 308–313. (  0) 0)
|
| [5] |
Zwaga J H and Driessen H. Tracking performance constrained MFR parameter control: Applying constraints on prediction accuracy[C]. Proceedings of the 8th International Conference on Information Fusion, Philadelphia, Pennsylvania, USA, 2005: 1–6.
( 0) 0)
|
| [6] |
Narykov A S, Krasnov O A, and Yarovoy A. Algorithm for resource management of multiple phased array radars for target tracking[C]. Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 2013: 1258–1264.
( 0) 0)
|
| [7] |
Shi Chen-guang, Wang Fei, Zhou Jian-jiang, et al.. Resource management for target tracking in distributed radar network system[C]. Proceedings of 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 2015: 1–5.
( 0) 0)
|
| [8] |
Lu Jian-bin, Hu Wei-dong, and Yu Wen-xian. Adaptive beam scheduling algorithm for an agile beam radar in multi-target tracking[C]. Proceedings of 2006 IEEE International Conference on Radar, Shanghai, China, 2006: 1–4.
( 0) 0)
|
| [9] |
鲁彦希, 何子述, 程子扬, 等. 多目标跟踪分布式MIMO雷达收发站联合选择优化算法[J].
雷达学报, 2017, 6(1): 73-80. Lu Yanxi, He Zishu, Cheng Ziyang, et al.. Joint selection of transmitters and receivers in distributed multi-input multi-output radar network for multiple targets tracking[J]. Journal of Radars, 2017, 6(1): 73-80. DOI:10.12000/JR16106 (  0) 0)
|
| [10] |
Yan Junkun, Liu Hongwei, Jiu Bo, et al.. Simultaneous multibeam resource allocation scheme for multiple target tracking[J].
IEEE Transactions on Signal Processing, 2015, 63(12): 3110-3122. DOI:10.1109/TSP.2015.2417504 ( 0) 0)
|
| [11] |
Yan Junkun, Liu Hongwei, Pu Wenqiang, et al.. Joint beam selection and power allocation for multiple target tracking in netted colocated MIMO radar system[J].
IEEE Transactions on Signal Processing, 2016, 64(24): 6417-6427. DOI:10.1109/TSP.2016.2607147 ( 0) 0)
|
| [12] |
Richards M A. Fundamentals of Radar Signal Processing[M]. New York: McGraw-Hill Education, 2005.
( 0) 0)
|
| [13] |
丁鹭飞, 耿富录. 雷达原理[M]. 西安: 西安电子科技大学出版社, 2006: 291–299.
Ding Lu-fei and Geng Fu-lu. Radar Principles[M]. Xi’an: Publishing House of Xidian University, 2006: 291–299. (  0) 0)
|
| [14] |
Van Trees H L. Detection, Estimation, and Modulation Theory, Part III: Radar-Sonar Signal Processing and Gaussian Signals in Noise[M]. New York: Wiley, 1971.
( 0) 0)
|
| [15] |
Van Trees H L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory[M]. New York: Wiley, 2002.
( 0) 0)
|
| [16] |
Tichavsky P, Muravchik C H and Nehorai A. Posterior Cramér-Rao bounds for discrete-time nonlinear filtering[J].
IEEE Transactions on Signal Processing, 1998, 46(5): 1386-1396. DOI:10.1109/78.668800 ( 0) 0)
|
| [17] |
Godrich H, Chiriac V M, Haimovich A M, et al.. Target tracking in MIMO radar systems: Techniques and performance analysis[C]. Proceedings of 2010 IEEE Radar Conference, Washington, DC, USA, 2010: 1111–1116.
( 0) 0)
|
| [18] |
Zuo Long, Niu Rui-xin and Varshney P K. Conditional posterior Cramér-Rao lower bounds for nonlinear sequential Bayesian estimation[J].
IEEE Transactions on Signal Processing, 2011, 59(1): 1-14. DOI:10.1109/TSP.2010.2080268 ( 0) 0)
|
| [19] |
Hernandez M L, Farina A and Ristic B. PCRLB for tracking in cluttered environments: Measurement sequence conditioning approach[J].
IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(2): 680-704. DOI:10.1109/TAES.2006.1642582 ( 0) 0)
|
| [20] |
Boyd S and Vandenberghe L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004.
( 0) 0)
|
| [21] |
Grant M, Boyd S, and Ye Y. CVX: Matlab software for disciplined convex programming[Z]. 2008.
( 0) 0)
|
| [22] |
Gustafsson F. Particle filter theory and practice with positioning applications[J].
IEEE Aerospace and Electronic Systems Magazine, 2010, 25(7): 53-82. DOI:10.1109/MAES.2010.5546308 ( 0) 0)
|
| [23] |
Arulampalam M S, Maskell S, Gordon N, et al.. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].
IEEE Transactions on Signal Processing, 2002, 50(2): 174-188. DOI:10.1109/78.978374 ( 0) 0)
|




