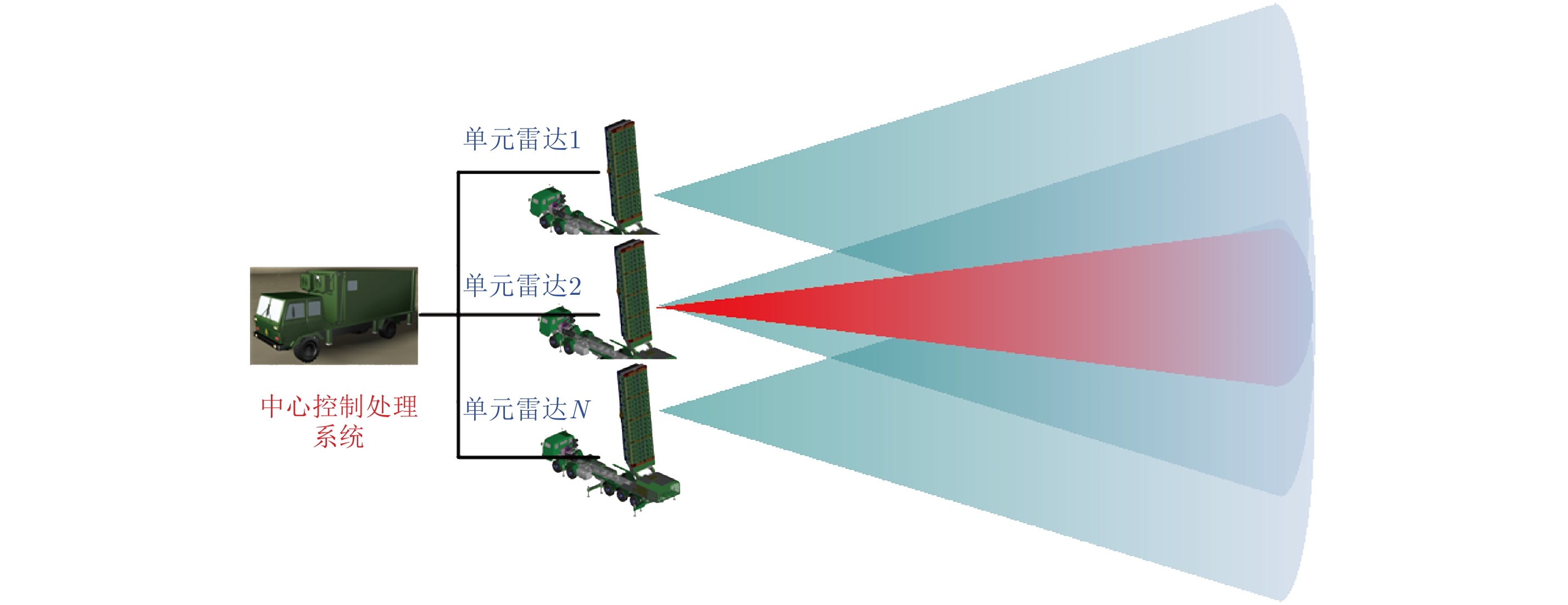
分布式孔径相参合成雷达是一种通过中心控制处理系统控制多个单元雷达实现电磁波空间能量合成的雷达系统[1,2],如图1所示。各单元雷达按一定的基线准则与布阵理论进行阵列布局,由中心控制处理系统统一控制调配,波束指向相同区域,并在中心控制处理系统控制下进行收发相参工作,实现收发信号全相参,实现目标远距离搜索发现和高精度跟踪测量[3]。分布式孔径相参合成雷达技术是解决平台约束与探测性能矛盾的有效手段,具有生存能力强、效费比高、角分辨率高、扩展性强、实现性好等技术优势,是雷达领域重要的发展方向[4–8]。
|
图 1 分布式孔径相参合成雷达示意图 Fig.1 Distributed aperture coherence-synthetic radar |
本文将在分布式孔径相参合成雷达体制下对联合天线增益进行分析和讨论。首先针对无方向性点源天线模型进行了联合天线增益分析,给出了理论推导和仿真结果;在此基础上建立了分布式孔径线阵模型,分别给出了单元方向图、联合孔径方向图和联合孔径增益仿真结果;最后,借助电磁仿真软件HFSS,构建了两单元分布式孔径相参合成雷达系统模型,进一步分析了联合孔径天线增益,并给出了分析结论。
2 多点源天线联合增益分析方向性系数D和增益G是表征天线辐射功率集中程度的重要参数,方向性系数定义为在总辐射功率相同的情况下,主瓣最大方向上的功率密度与全空间的平均功率密度之比,数学表达式为[9,10]:
|
$D = \frac{{4{{π}} {{\left| {{F_{\max }}} \right|}^2}}}{{\displaystyle\int_0^{2{{π}} } {{\rm d}\varphi } \int_0^{{π}} {{{\left| {F\left( {\theta ,\varphi } \right)} \right|}^2}\sin \theta {\rm d}\theta } }}$
|
(1) |
式中,
|
$D = \frac{{4{{π}} A}}{{{\lambda ^2}}}$
|
(2) |
增益G等于方向性系数乘以天线效率[11],即
|
$G = \eta D$
|
(3) |
天线方向性系数侧重于天线辐射功率集中程度的理论指标,而增益则侧重于天线辐射功率集中程度的工程实现指标,由于天线效率不会对本文的分析结果产生影响,因此,本文不对天线方向性系数和增益做特殊区分。
设分布式孔径相参合成雷达由N个无方向性的相同点辐射源天线组成,各天线单元间距为d,呈直线排布,多点源天线联合方向图表达式为:
|
$\begin{aligned}\\F\left( \theta \right) = \sum\limits_{i = 0}^{N - 1} {{{\rm e}^{{\rm j} \Large\frac{{2{{π}} id\sin \theta }}{\lambda }}}} \end{aligned}$
|
(4) |
式中,
|
$\begin{align}
& {{\left| F\left( \theta \right) \right|}^{2}}=F\left( \theta \right){{F}^{*}}\left( \theta \right)=\sum\limits_{i=0}^{N-1}{{{\text{e}}^{\text{j}\frac{2\pi id\sin \theta }{\lambda }}}}\sum\limits_{i=0}^{N-1}{{{\text{e}}^{-\text{j}\frac{2\pi id\sin \theta }{\lambda }}}} \\
& =N+2\sum\limits_{i=1}^{N-1}{\left( N-i \right)\cos \left( \frac{2\pi id\sin \theta }{\lambda } \right)} \\
\end{align} $
|
(5) |
对式(5)进行归一化处理,得到
|
${{\left| F\left( \theta \right) \right|}^{2}}=\frac{1}{N}+\frac{2}{{{N}^{2}}}\sum\limits_{i=1}^{N-1}{\left( N-i \right)\cos \left( \frac{2\pi id\sin \theta }{\lambda } \right)}$
|
(6) |
归一化后
|
$\begin{aligned}D & = \frac{{4{{π}} }}{{\displaystyle\int_0^{2{{π}} } {{\rm d}\varphi } \int_0^{{π}} {{{\left| {F\left( \theta \right)} \right|}^2}\sin \theta {\rm d}\theta } }}\\ & = \displaystyle\frac{{4{{π}} }}{{\displaystyle\frac{{4{{π}} }}{N} + \displaystyle\frac{{8{{π}} }}{{{N^2}}}\sum\limits_{i = 1}^{N - 1} {\left( {N - i} \right) \frac{{\sin \left( { \Large\frac{{2{{π}} id\sin \theta }}{\lambda }} \right)}}{{\displaystyle\frac{{2{{π}} id\sin \theta }}{\lambda }}}} }}\\ & = \frac{1}{{\displaystyle\frac{1}{N} + \displaystyle\frac{2}{{{N^2}}}\sum\limits_{i = 1}^{N - 1} {\left( {N - i} \right) \frac{{\sin \left( { \Large\frac{{2{{π}} id\sin \theta }}{\lambda }} \right)}}{{ \Large\frac{{2{{π}} id\sin \theta }}{\lambda }}}} }}\end{aligned}$
|
(7) |
为验证多点源天线联合增益特征,在满足式(7)的条件下改变各天线单元间距d和单元雷达个数N,设雷达工作频率为10 GHz,且各单元雷达等间距排布,仿真结果如图2所示。

|
图 2 多点源天线联合增益仿真结果 Fig.2 Multipoint source antenna joint gain simulation results |
通过图2可以发现,随着单元雷达间距的增加,多点源天线联合增益从剧烈震荡慢慢趋于稳定,且多点源天线联合增益的震荡强度随着单元雷达数目的增多而增强,但最终趋于的稳定值与单元雷达数目相等。结合实际应用,单元雷达间距通常在米量级以上,即X波段大于30倍波长,C波段大于15倍波长,此时,联合天线增益趋于稳定值,受单元雷达间距影响较小,与单元雷达数目和单元雷达天线增益有关,近似表达式为:
|
$G \approx {N_{\rm r}}{G_0}$
|
(8) |
其中,Nr为单元雷达个数,G0为单元雷达天线增益。
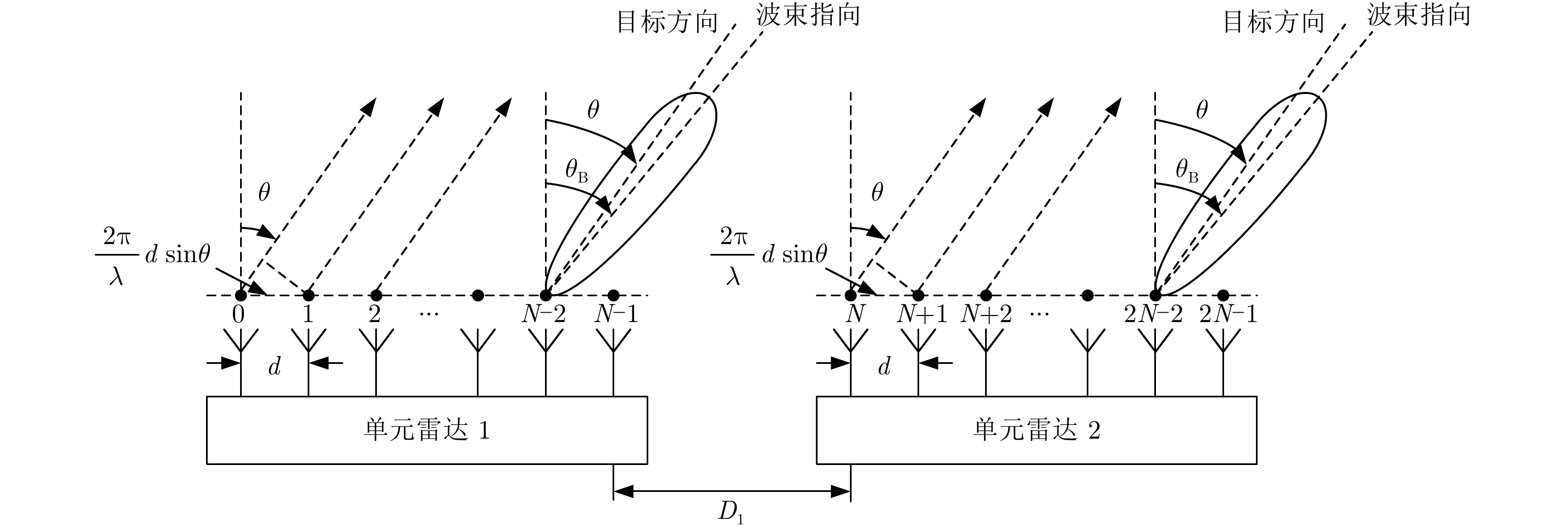
3 分布式阵列联合天线增益分析 3.1 联合天线方向图 3.1.1 分布式阵列几何关系阵列天线的结构形式是多种多样的,最基本的形式是1维线阵,以两单元雷达为例,对联合天线方向图及联合天线增益进行分析。如图3所示为分布式阵列天线几何关系,单元雷达间距为D1,单元雷达阵元个数为N,阵元间距为d,方位扫描角为
|
图 3 分布式阵列天线几何关系 Fig.3 Distributed array antenna geometric relationship |
单元雷达线阵天线方向图函数表达式为:
|
$\begin{aligned}\\\left| {{F_{\rm e}}\left( \theta \right)} \right| = \frac{{\sin\left( {\displaystyle\frac{{N {π} }}{\lambda }d\left( {\sin \theta - \sin {\theta _{\rm B}}} \right)} \right)}}{{\sin \left( {\displaystyle\frac{{π} }{\lambda }d\left( {\sin \theta - \sin {\theta _{\rm B}}} \right)} \right)}}\end{aligned}$
|
(9) |
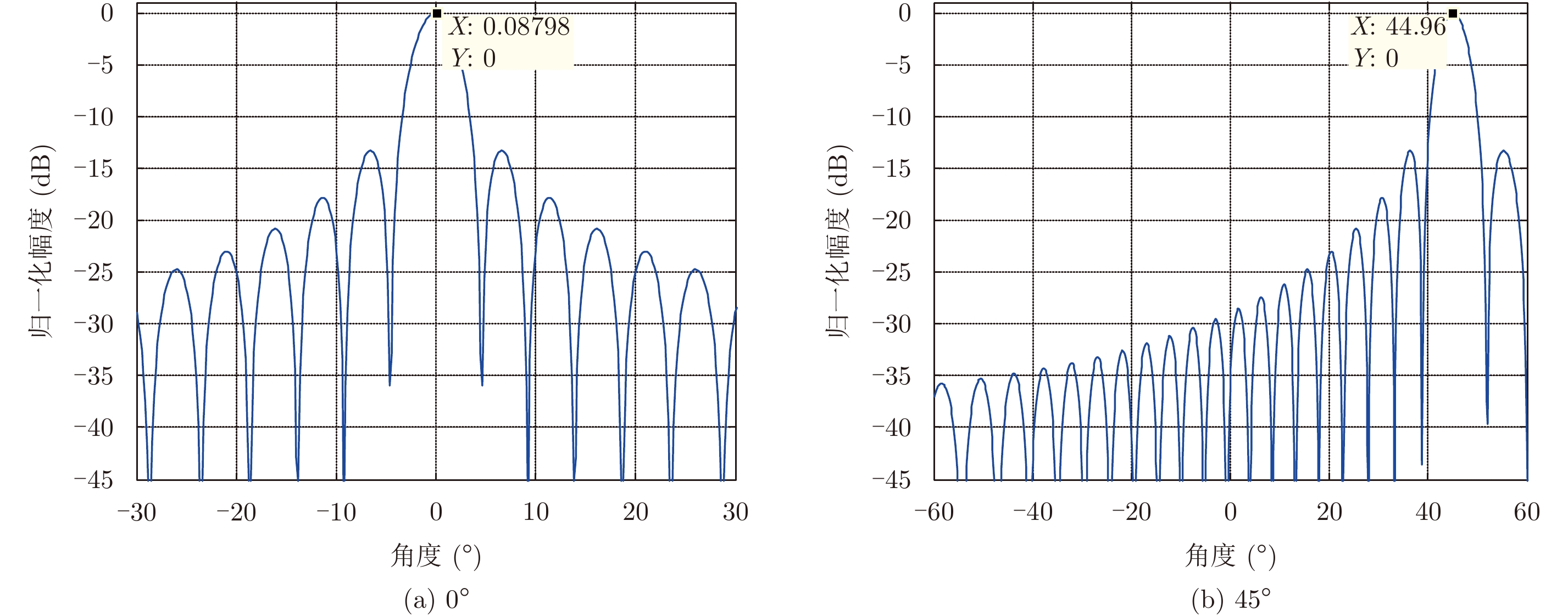
单元雷达方向图仿真结果如图4所示,仿真参数为:阵元个数为25个,阵元间距为半波长,发射信号载频为10 GHz。
|
图 4 单元雷达天线方向图 Fig.4 Unit radar antenna pattern |
以单元雷达1为基准,阵元编号为
|
$\begin{aligned}\left| {F\left( \theta \right)} \right| = & 2\cos \left( {\frac{{π} }{\lambda }\left( {{D_1} + Nd} \right)\left( {\sin \theta - \sin {\theta _{\rm B}}} \right)} \right)\\ &\cdot \frac{{\sin \left( { \displaystyle\frac{{N{π} d}}{\lambda }\left( {\sin \theta - \sin {\theta _{\rm B}}} \right)} \right)}}{{\sin \left( {\displaystyle\frac{{{π} d}}{\lambda }\left( {\sin \theta - \sin {\theta _{\rm B}}} \right)} \right)}}\end{aligned}$
|
(10) |
当分布式孔径相参合成雷达由多部单元雷达组成时,根据方向图相乘原理,分布式阵列联合天线方向图可表示为阵因子与单元雷达天线方向图的乘积形式,表达式为:
|
$\begin{aligned}& \\& F(\theta ) = {F_{\rm{a}}}(\theta ) \cdot {F_{\rm{e}}}(\theta )\end{aligned}$
|
(11) |
式中,
|
${F_{\rm{a}}}(\theta ) = \sum\limits_{m = 1}^M {\exp \left( {{\rm j}\frac{{2{{π}} }}{\lambda }{{\mathop D\nolimits} _m}\left( {\sin \theta - \sin {\theta _{\rm{B}}}} \right)} \right)} $
|
(12) |
式中,M为单元雷达数目,以单元雷达1的相位参考点o作为雷达阵列的相位参考点,第m部单元雷达相位参考点到o点的距离为
|
$\left| {{F_{\rm{a}}}(\theta )} \right| = \frac{{\sin \left( {\displaystyle\frac{{M{{π}} {D_1}}}{\lambda }\left( {\sin \theta - \sin {\theta _{\rm{B}}}} \right)} \right)}}{{\sin \left( {\displaystyle\frac{{{{π}} {D_1}}}{\lambda }\left( {\sin \theta - \sin {\theta _{\rm{B}}}} \right)} \right)}}$
|
(13) |
联合天线方向图仿真结果如图5所示,单元雷达阵元数为25,图5(a)为雷达间距D1=10倍波长时的联合天线方向图,图5(b)为雷达间距D1=50倍波长时的联合天线方向图,通过图形可以发现,随着雷达间距D1的不断增加,联合天线方向图的栅瓣也将越来越多。

|
图 5 分布式阵列与单元雷达天线方向图比较 Fig.5 Antenna pattern comparison between distributed array and unit radar |
为了进一步验证联合天线方向图栅瓣情况,利用C波段相控阵体制分布式孔径相参合成雷达原理样机进行了变基线联合天线方向图测试试验,雷达原理样机实物如图6所示。

|
图 6 雷达原理样机 Fig.6 Radar prototype |
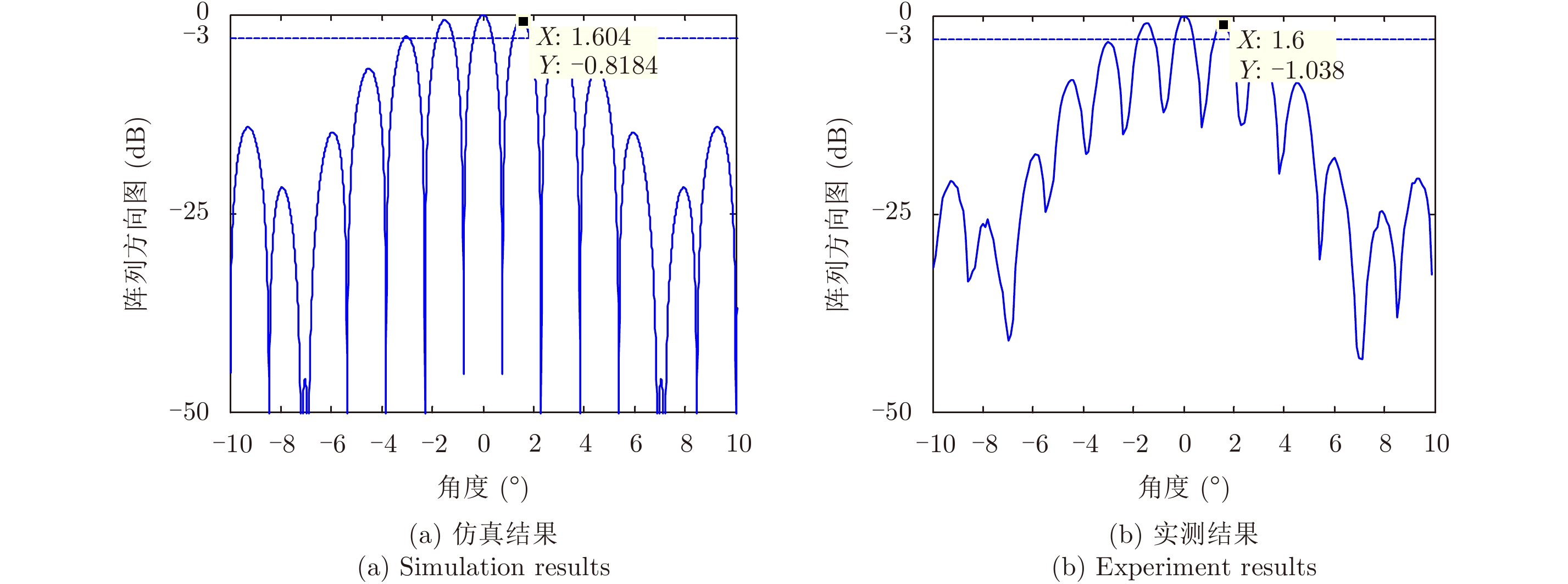
试验中改变两个天线相位中心的基线长度,测试不同基线长度下的联合天线方向图。如图7和图8所示,分别给出了基线间距为1.229 m和2.116 m条件下联合天线方向图实测结果和仿真结果,对比试验数据与仿真结果,栅瓣位置基本吻合,栅瓣数目相同,且基线距离越大,栅瓣数量越多,栅瓣间距越小。
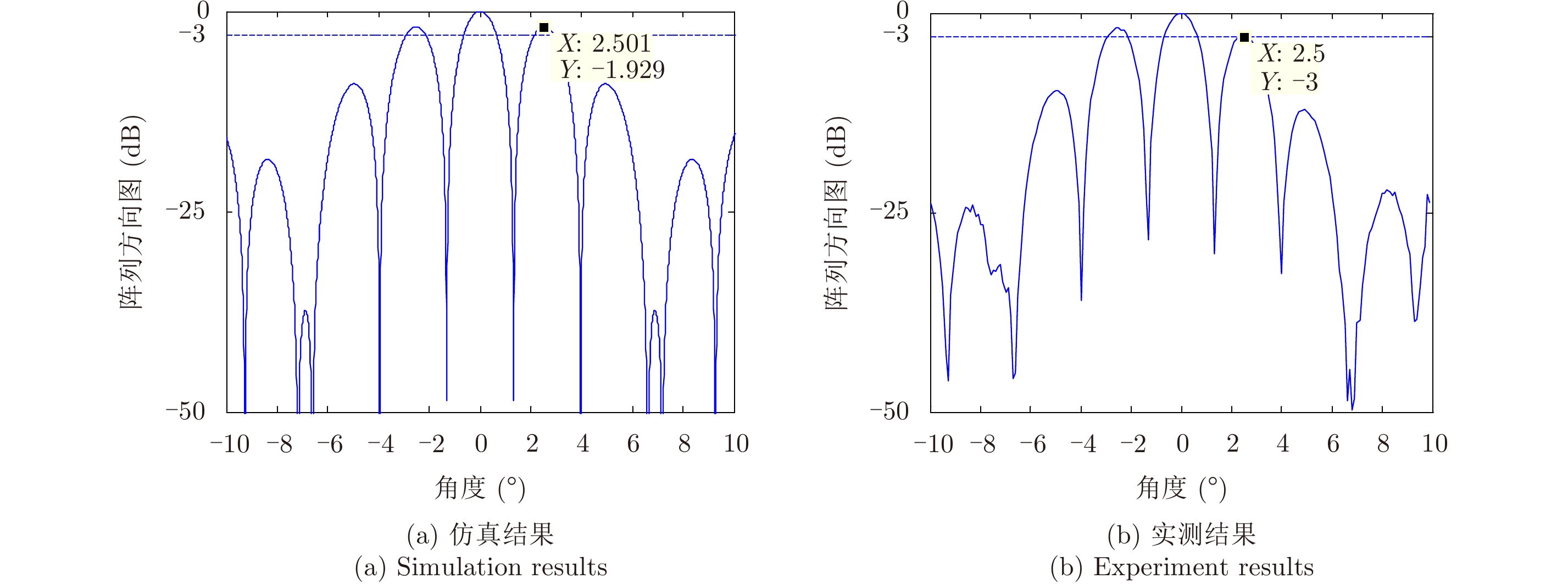
|
图 7 联合天线方向图(D1=1.229 m) Fig.7 Joint antenna pattern (D1=1.229 m) |
|
图 8 联合天线方向图(D1=2.116 m) Fig.8 Joint antenna pattern (D1=2.116 m) |
栅瓣是否会对雷达的联合天线增益产生影响,多单元雷达联合增益是否会随单元雷达间距的变化而变化,3.2节将做进一步分析。
3.2 联合天线增益根据图3建立的分布式阵列天线几何模型,可计算出两单元雷达线阵联合天线方向图为:
|
$\begin{aligned}F\left( \theta \right) = & \sum\limits_{i = 0}^{N - 1} {{{\rm e}^{{\rm j} \scriptsize\displaystyle\frac{{2{{π}} id}}{\lambda }\left( {\sin \theta - \sin {\theta _{\rm{B}}}} \right)}}} \\ \cdot & \Biggr( {1 + {{\rm e}^{{\rm j} \scriptsize\displaystyle\frac{{2{{π}} }}{\lambda }\left( {D_1 + Nd} \right)\left( {\sin \theta - \sin {\theta _{\rm{B}}}} \right)}}} \Biggr)\end{aligned}$
|
(14) |
对联合天线方向图进行归一化处理,有
|
$\begin{aligned}&\\{\left| {F\left( \theta \right)} \right|^2} & \!\!=\!\! \left(\! {2\!\! +\!\! 2\cos\! \left( {\frac{{2{{π}} }}{\lambda }\left( {D_1 \!\!+\!\! Nd} \right)\left( {\sin \theta \!\! -\!\! \sin {\theta _{\rm{B}}}} \right)} \right)}\!\! \right) \!\\& \cdot \!\! \left(\!\!\! {\frac{1}{N} \!\!+\!\! \frac{2}{{{N^2}}}\sum\limits_{i = 1}^{N - 1} \!{\left( {\!N \!\!-\!\! i} \right)\! \cos\!\! \left(\!\! {\frac{{2{{π}} id}}{\lambda }\left( {\sin \theta \!\!-\!\!\! \sin {\theta _{\rm{B}}}} \right)}\! \right)} }\!\!\! \right)\end{aligned}$
|
(15) |
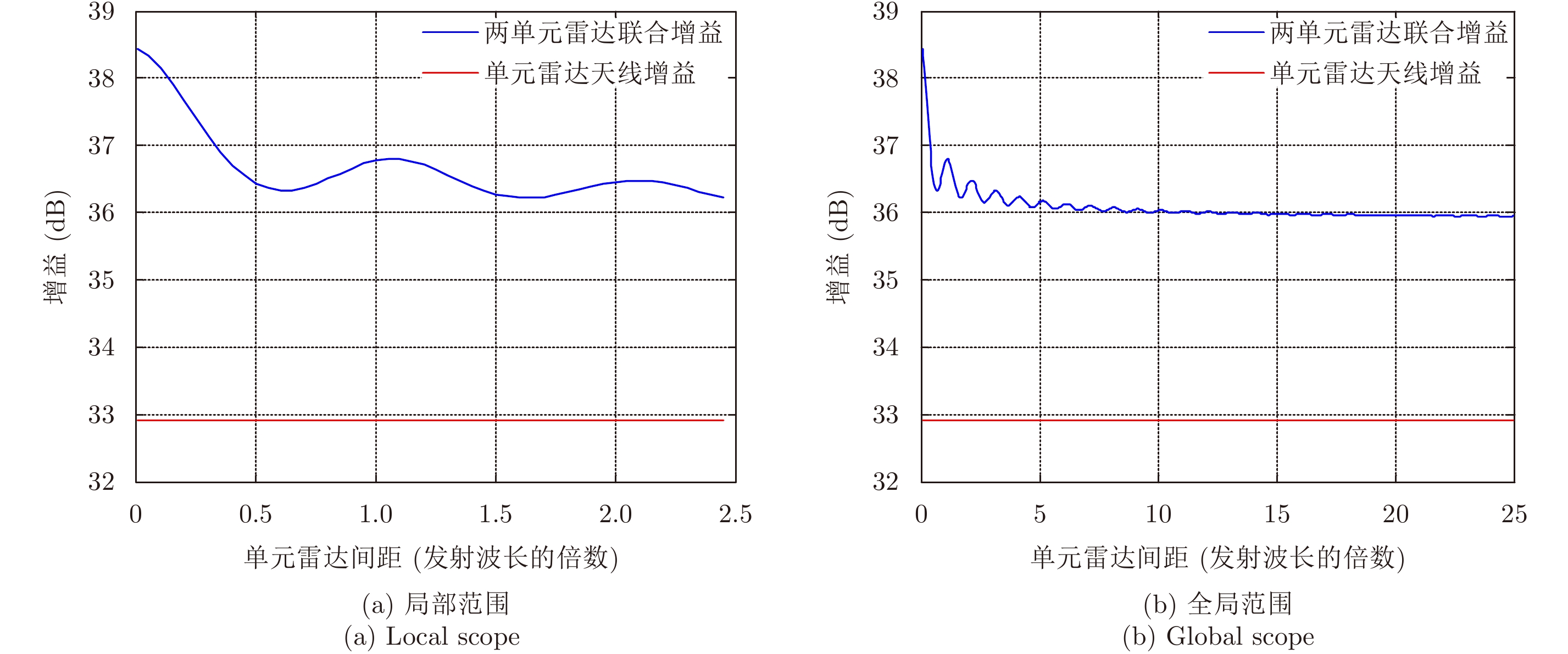
将式(15)代入式(7)即可获得两单元雷达的联合天线增益,但由于联合天线增益表达式的积分项求解十分复杂,因此,本文采用数值积分法进行仿真计算,仿真结果如图9所示。
|
图 9 两单元雷达联合天线增益 Fig.9 Two unit radar joint antenna gain |
通过图9可以发现,当单元雷达间距大于一定波长倍数时,联合天线增益趋于稳定值,近似为单元雷达增益的2倍,此结果与点源天线联合增益仿真结果相符,从侧面也反映出栅瓣的产生不会影响联合天线的增益,具体原因分析为,虽然栅瓣的出现消耗了雷达辐射的功率,但雷达主瓣内的辐射电磁波功率密度是增加的,增加倍数近似等于单元雷达个数。
3.3 基于HFSS软件的联合天线增益仿真本节将使用HFSS仿真软件对两单元分布式孔径相参合成雷达联合天线增益进行仿真分析。
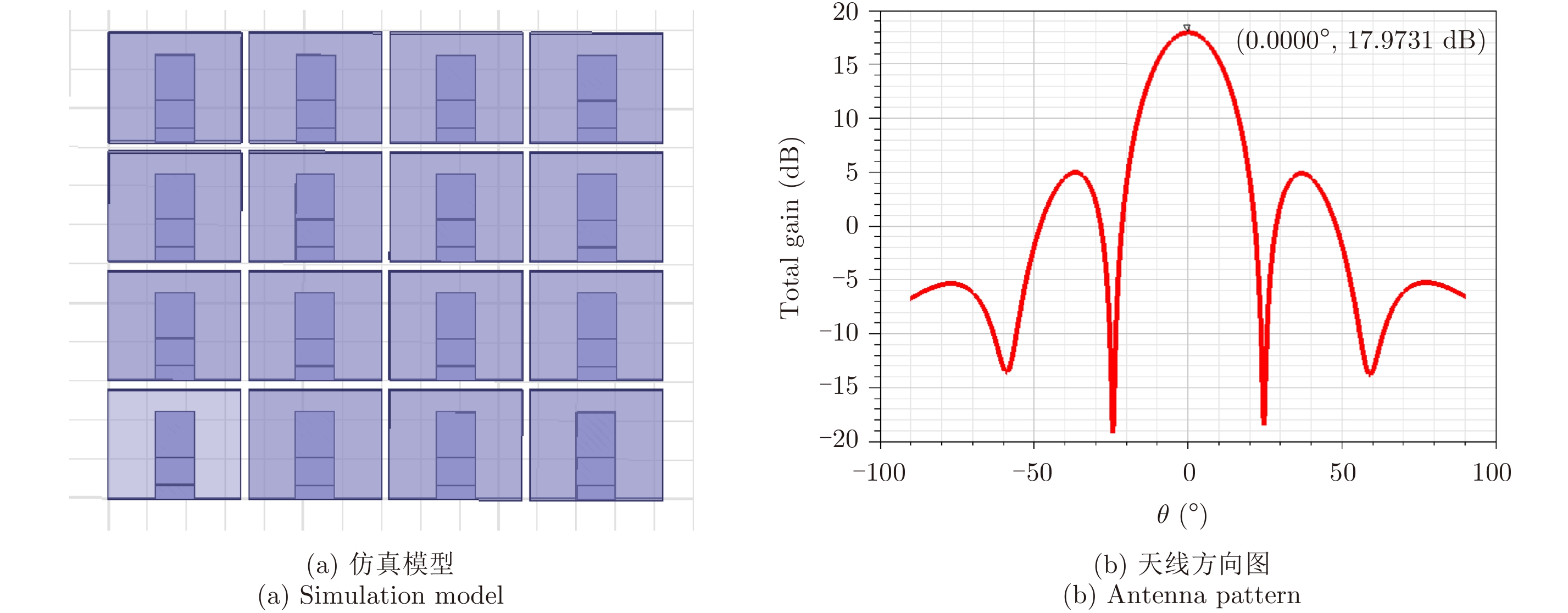
3.3.1 单元雷达模型 单元雷达为一个4×4阵元的面阵,工作频段为5 GHz,阵元间距为半波长,阵面口径为122 mm×144 mm,如图10(a)所示。单元雷达天线方向图和增益如图10(b)所示,单元雷达天线增益为17.9731 dB。
|
图 10 单元雷达仿真模型及天线方向图 Fig.10 Unit radar simulation model and antenna pattern |
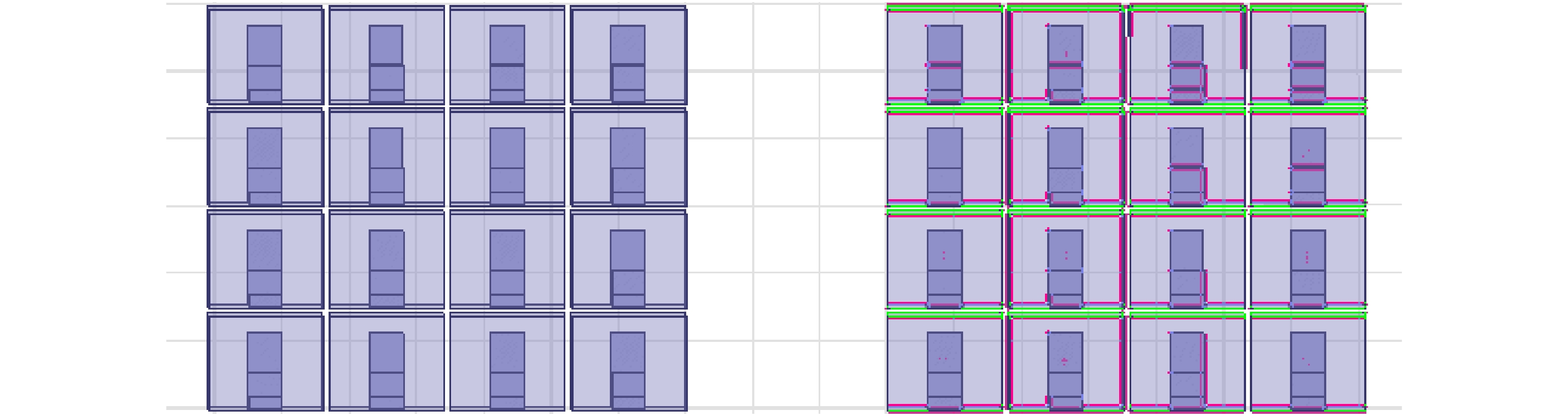
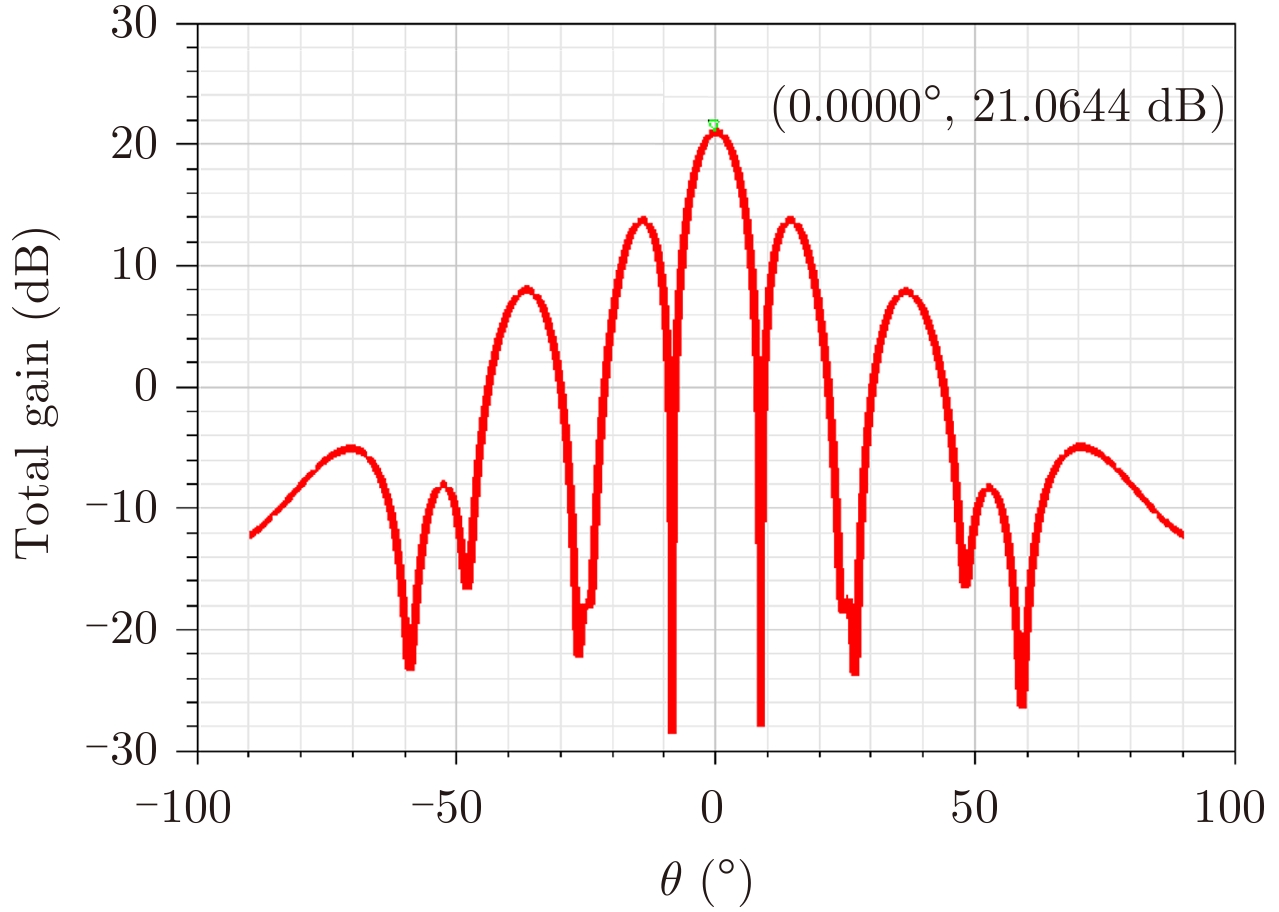
3.3.2 两单元分布式雷达模型 利用HFSS仿真软件构建了两单元分布式孔径相参合成雷达系统,单元雷达间距可调,如图11所示,当单元雷达间距为60 mm时,对应的天线方向图如图12所示,两单元雷达联合天线增益为21.064 dB,较单元雷达天线增益增加了3.09 dB,约为单元雷达天线增益的2倍(3.01 dB)。
|
图 11 分布式孔径相参合成雷达仿真模型 Fig.11 Distributed Aperture Coherence-synthetic Radar simulation model |
|
图 12 联合天线方向图 Fig.12 Joint antenna pattern |
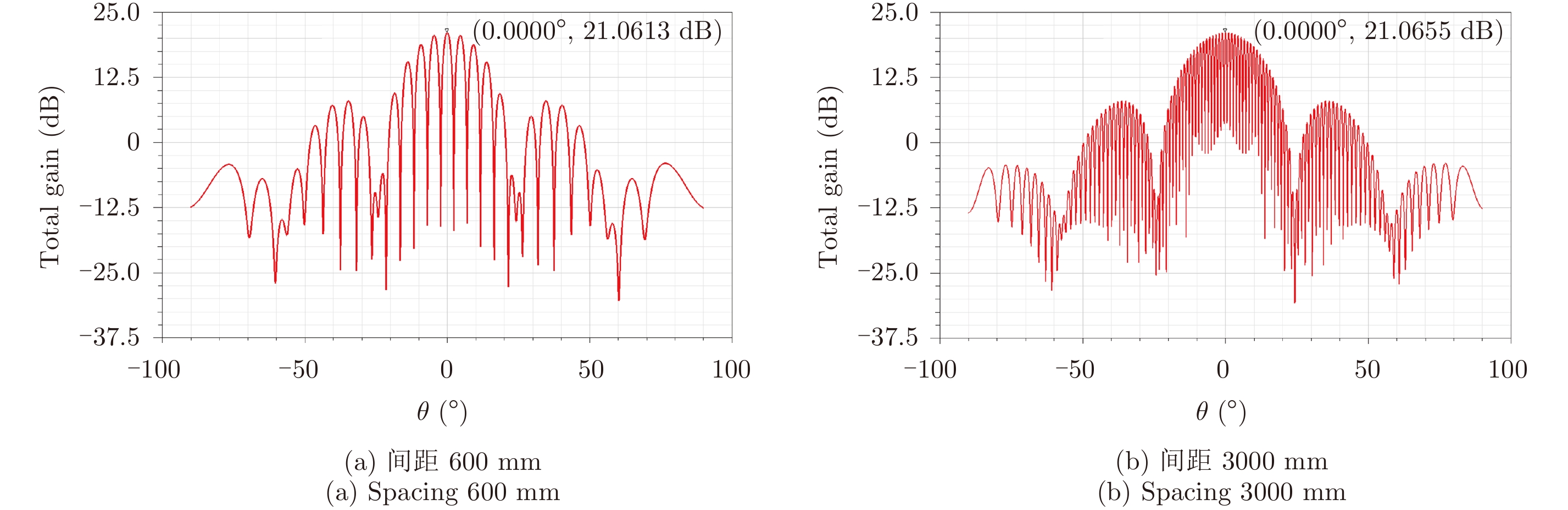
为了从不同雷达间距分析联合天线增益情况,图13分别给出了600 mm和3000 mm两种典型间距联合天线方向图,增益分别为21.0613 dB和21.0655 dB,较单元雷达天线增益均增加了3 dB。
|
图 13 联合天线方向图 Fig.13 Joint antenna pattern |
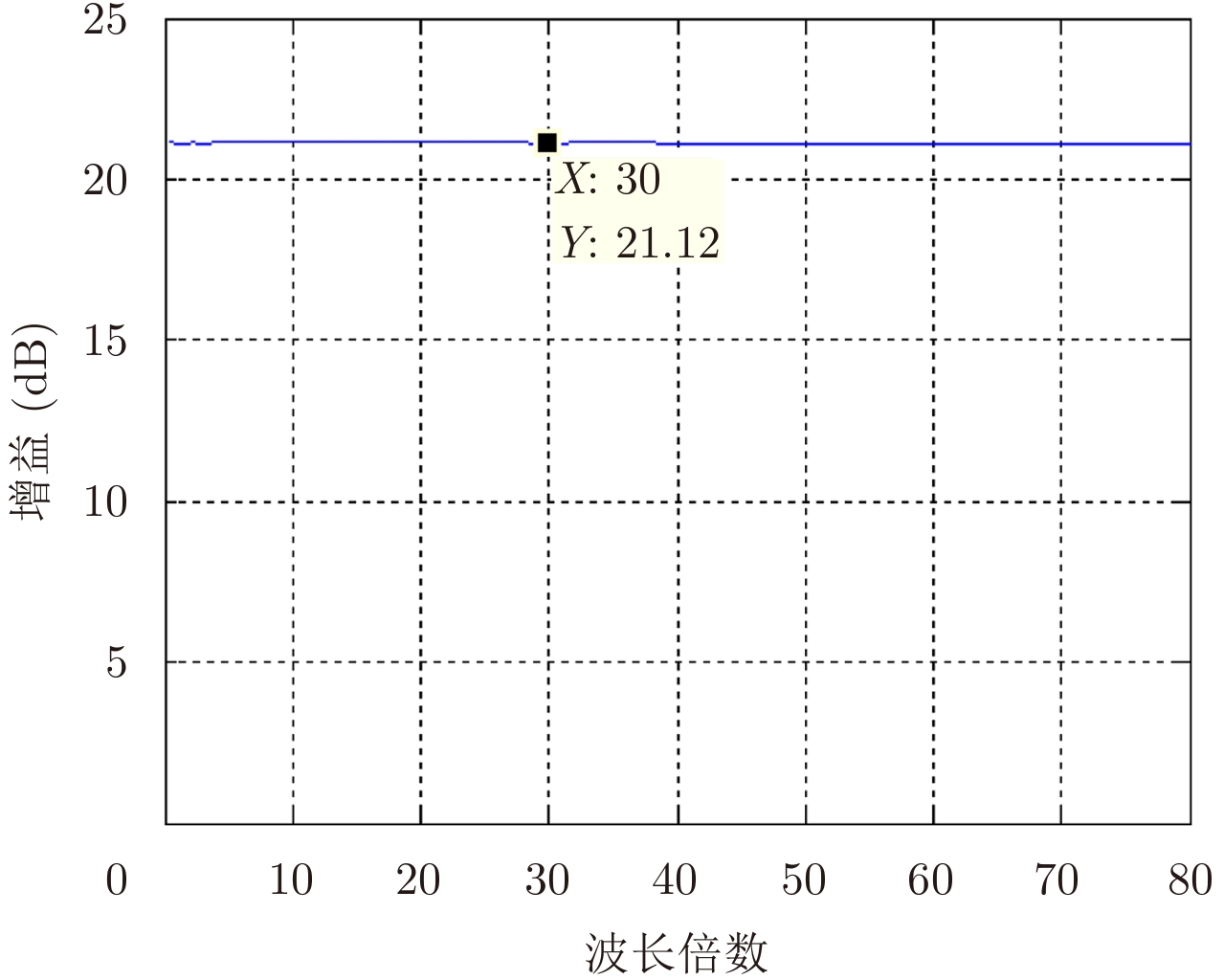
如图14所示为分布式孔径相参合成雷达不同间距条件下联合天线增益统计图,通过图形可以发现,统计曲线较为平坦,联合天线增益均值为21.12 dB,相比于单元天线增益17.9731 dB增加了约3 dB,即为单元雷达天线增益的2倍,从而进一步验证了联合天线增益受单元雷达间距的影响较小,与单元雷达个数和单元雷达增益有关的结论。
|
图 14 联合天线增益统计图 Fig.14 Joint antenna gain statistics |
文章首先对多单元点辐射源天线的联合增益进行了分析,在单元雷达间距大于一定波长倍数时,由多个无方向性的点辐射源天线构成的分布式孔径相参合成雷达的联合天线增益趋于稳定,只与单元雷达数目和单元雷达增益有关;然后对两单元线阵天线的联合增益进行了分析,讨论栅瓣对联合增益的影响;最后,利用HFSS软件仿真分析了两单元阵列雷达的联合天线增益,进一步验证了联合天线增益近似等于单元雷达数目与单元雷达增益乘积的结论。
| [1] |
鲁耀兵, 高红卫, 周宝亮. 分布式孔径相参合成雷达技术[J].
雷达学报, 2017, 6(1): 55-64. Lu Yaobing, Gao Hongwei and Zhou Baoliang. Distributed aperture coherence-synthetic radar technology[J]. Journal of Radars, 2017, 6(1): 55-64. (  0) 0)
|
| [2] |
鲁耀兵, 张履谦, 周荫清, 等. 分布式阵列相参合成雷达技术研究[J].
系统工程与电子技术, 2013, 35(8): 1657-1662. Lu Yao-bing, Zhang Lv-qian, Zhou Yin-qing, et al.. Study on distributed aperture coherence-synthetic radar technology[J]. Systems Engineering and Electronics, 2013, 35(8): 1657-1662. DOI:10.3969/j.issn.1001-506X.2013.08.12 (  0) 0)
|
| [3] |
Coutts S, Cuomo K, McHarg J, et al.. Distributed coherent aperture measurements for next generation BMD radar[C]. Proceedings of the Fourth IEEE Workshop on Sensor Array and Multichannel Processing, Waltham, MA, 2006: 390–393.
( 0) 0)
|
| [4] |
Brookner E. Phased-array and radar breakthroughs[C]. Proceedings of 2007 IEEE Radar Conference, Boston, MA, USA, 2007: 37–42.
( 0) 0)
|
| [5] |
Brookner E. Phased-array and radar astounding breakthroughs—An update[C]. Proceedings of IEEE Radar Conference, Rome, Italy, 2008: 1–6.
( 0) 0)
|
| [6] |
曹哲, 柴振海, 高红卫, 等. 分布式阵列相参合成雷达技术研究与试验[J].
现代防御技术, 2012, 40(4): 1-11. Cao Zhe, Chai Zhen-hai, Gao Hong-wei, et al.. Technology and tests on distributed aperture coherence-synthesizing radar[J]. Modern Defence Technology, 2012, 40(4): 1-11. (  0) 0)
|
| [7] |
高红卫, 曹哲, 鲁耀兵. 分布式阵列相参合成雷达基本研究与原理验证[C]. 第十二届全国雷达学术年会论文集, 武汉, 中国, 2012: 129–134.
Gao Hong-wei, Cao Zhe, and Lu Yao-bing. Basic study and principle validate of distributed aperture coherence-synthetic radar[C]. Proceedings of the 12th Chinese Radar Conference, Wuhan, China, 2012: 129–134. (  0) 0)
|
| [8] |
Gao Hong-wei and Zhou Bao-liang. Performance analysis and experimental study on distributed aperture coherence-synthetic radar[C]. 2016 CIE Radar Conference, Guangzhou, China, 2016.
( 0) 0)
|
| [9] |
Stutzman W L and Thiele G A. Antenna Theory and Design[M]. New York: John Wiley & Sons, 1981: 141–145.
( 0) 0)
|
| [10] |
王建, 郑一农, 何子远. 阵列天线理论与工程应用[M]. 北京: 电子工业出版社, 2015: 15–18.
Wang Jian, Zheng Yi-nong, and He Zi-yuan. Antenna Array Theory and Engineering Applications[M]. Beijing: Publishing House of Electronics Industry, 2015: 15–18. (  0) 0)
|
| [11] |
张祖稷, 金林, 束咸荣. 雷达天线技术[M]. 北京: 电子工业出版社, 2005: 20–21.
Zhang Zu-ji, Jin Lin, and Shu Xian-rong. Radar Antenna Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 20–21. (  0) 0)
|




