② (中国科学院大学 北京 100190)
③ (华讯方舟科技有限公司 深圳 518000)
② (University of Chinese Academy of Sciences, Beijing 100190, China)
③ (China Communication Technology Co., Ltd., Shenzhen 518000, China)
人体安检成像技术是近年来安检领域的研究热点[1],其中主动式人体安检成像系统因其受环境因素影响小、图像信噪比高等优点而被广泛应用[2]。由于违禁物品往往具有隐蔽性,而毫米波能够穿透衣物和部分绝缘体遮挡、回波衰减率较小、对人体无害,因此利用毫米波作为载体的人体安检成像技术已成为目前最具潜力的安检成像技术之一[3]。
2003年,美国L3通信公司研制了ProVision毫米波人体扫描仪[4]。该设备工作频率为 24~30 GHz,所采用的图像处理技术可获得5 mm横向分辨率,目前在美国、欧洲及亚洲等部分机场均有使用。2011年,德国埃尔兰根-纽伦堡大学微波光子研究所搭建了多基地毫米波快速成像系统[5,6]。该原型系统工作频率为70~80 GHz,所获得的成像结果横向分辨率为2 mm;采用一个2 m×1 m大小的2维平面稀疏阵列,平板式数据获取时间可达到50 ms以下,可实现人体目标实时成像。
本文在上述研究背景下,首先基于柱面扫描成像模型,提出一种基于巴克码的稀疏采样方式和基于干涉处理[7]频域压缩感知(Compressed Sensing, CS)的频域稀疏毫米波人体安检3维成像方法,以降低安检系统数据采集量,实际数据处理结果验证了算法的有效性。其次基于文献[5]的快速成像系统,设计一种基于巴克码和收发分置模式的稀疏平面阵列,进一步降低硬件成本。
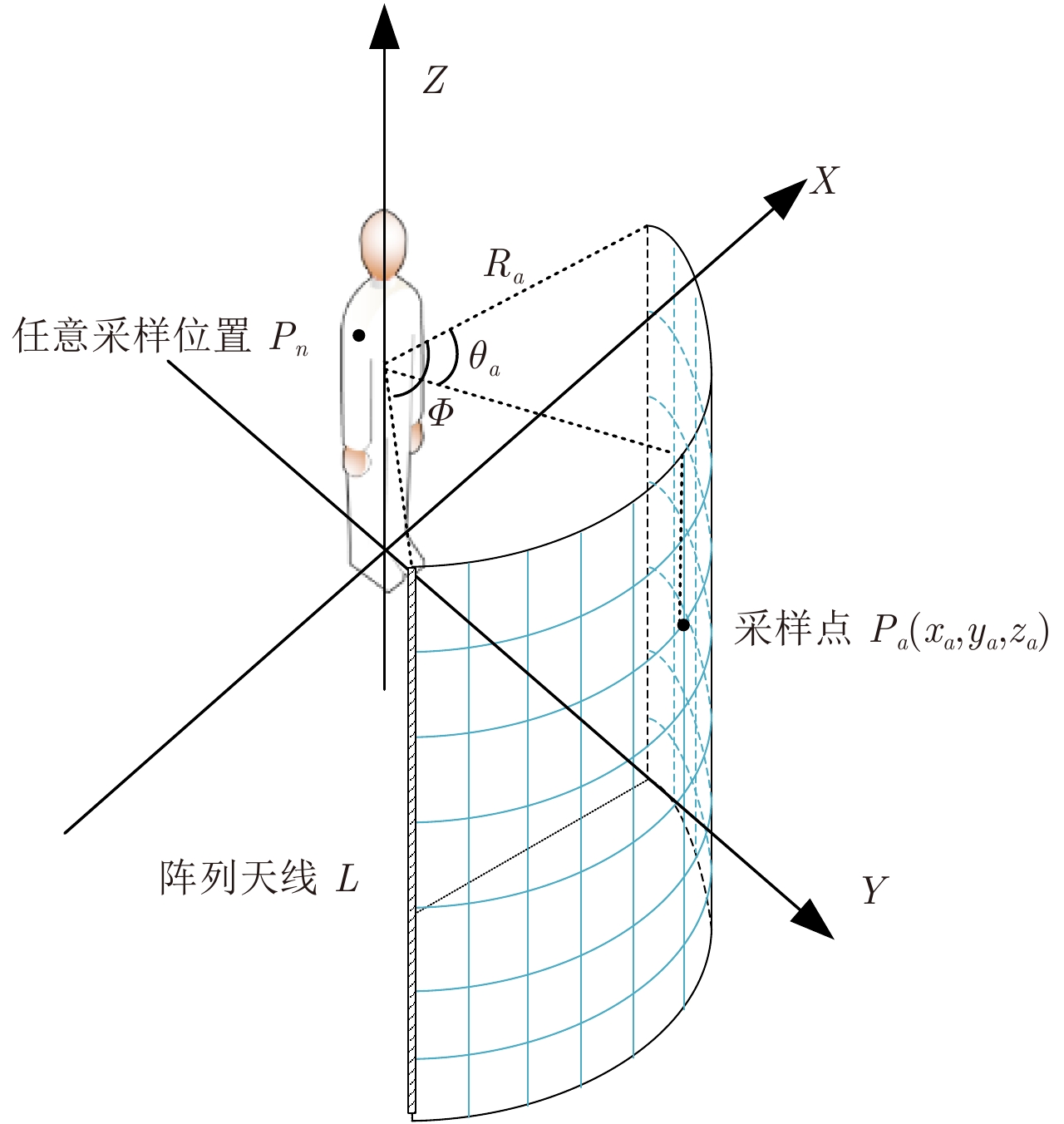
2 成像模型及信号处理 2.1 柱面扫描3维成像模型毫米波人体安检柱面扫描3维成像模型如图1所示,图中以人体中心为坐标原点建立直角坐标系,其中X轴表示方位向(横向),Y轴表示距离向,Z轴表示高度向(纵向);1维天线阵列长度为L,且以坐标原点为圆心、测试距离Ra为半径进行扫描,形成圆心角为
|
图 1 毫米波人体安检柱面扫描3维成像模型 Fig.1 The cylindrical scanning 3-D imaging model of a millimeter wave human security system |
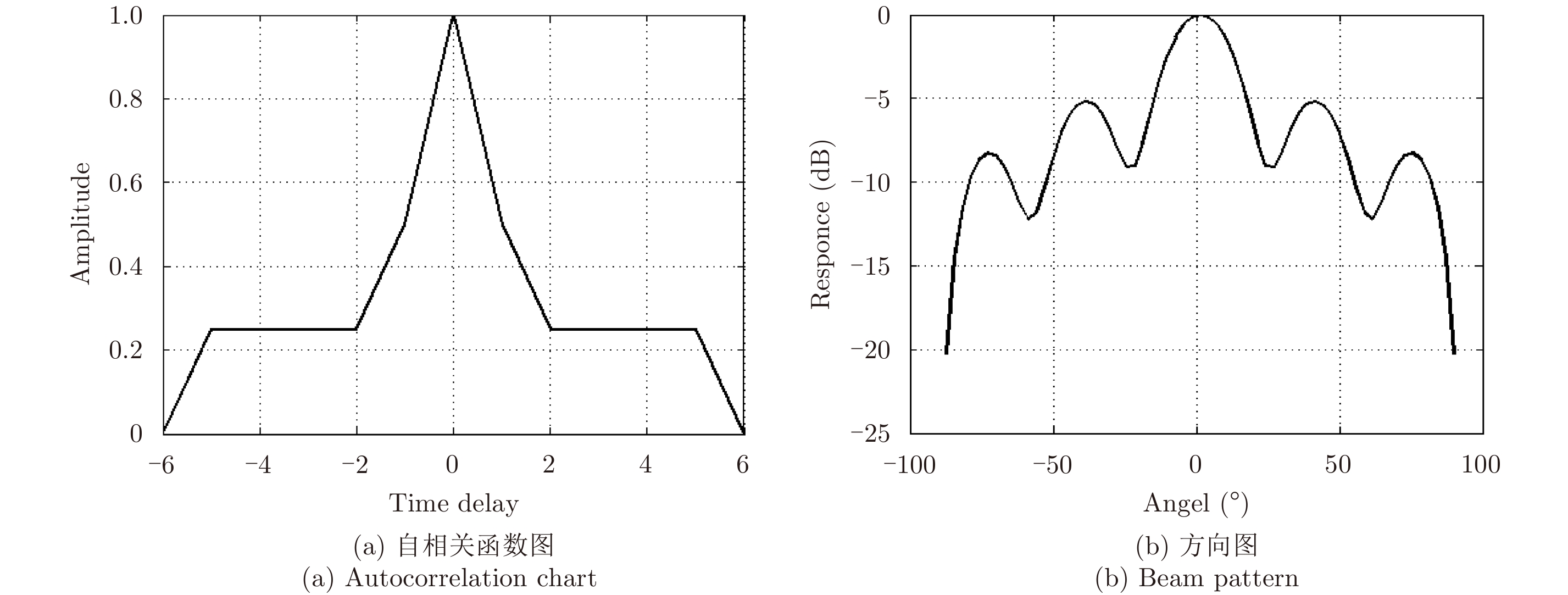
为减少数据获取时间、提高扫描速度,在方位向采用稀疏采样方式,但稀疏采样会使图像产生栅瓣和高副瓣。选择合适的采样准则可改善图像质量,本文采用巴克码伪随机序列[8,9]作为稀疏采样准则。巴克码具有尖锐的自相关函数和良好的随机性,稀疏率约50%,其中长度为7的巴克码[1110010]对应的自相关函数图和方向图如图2所示。从图中可知以巴克码为稀疏采样准则可有效避免图像栅瓣和副瓣带来的能量泄露。
|
图 2 巴克码[1110010]的自相关函数图和方向图 Fig.2 The Autocorrelation and Beam pattern diagrams for Barker code of [1110010] |
假设天线发射信号为
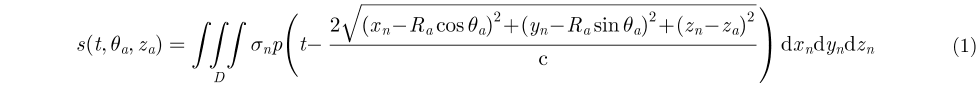
|
其中,D为人体成像区域范围。对式(1)在快时域进行傅里叶变换
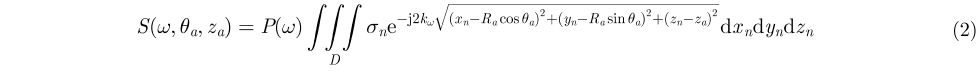
|
其中,
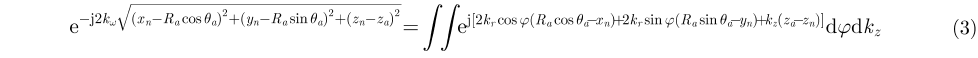
|
假设
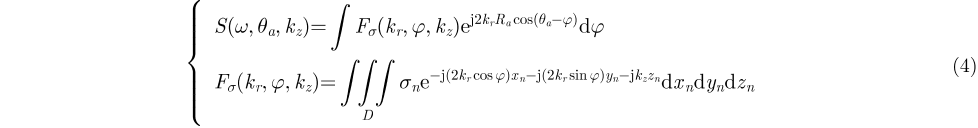
|
式中,
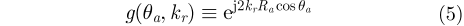
|
则有
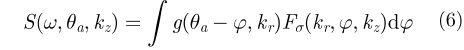
|
对
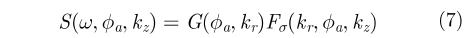
|
由式(7)可知,构造形如
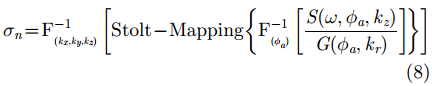
|
当方位向采用稀疏采样方式时,采用上述基于波数域匹配滤波(Match Filtering, MF)的成像方法会引起图像混叠。对此本文提出一种基于干涉处理和频域CS的3维成像算法,在稀疏采样条件下重建图像。由式(6)可知,稀疏采样得到的回波信号可写成如下离散形式:
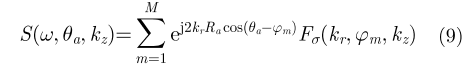
|
其中,M为方位向成像单元个数。在第i个距离向波数

|
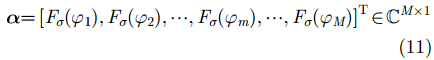
|
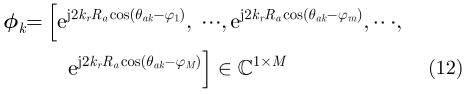
|
其中,
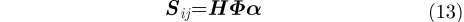
|
其中,
由于人体目标在空间域为连续分布,其图像在频域应具有稀疏性。但在毫米波人体复图像中,由于分辨单元间复散射系数不同、空间采样间隔通常远大于波长,其图像分辨单元初始相位是随机变化的[11],该随机初始相位主要是由于斜距方向分辨单元间复散射系数不同和斜距方向采样间隔较大而产生,由此使复图像频谱
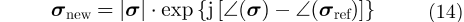
|
由于两幅图像
由式(14)可知,待重建复图像
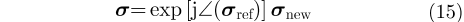
|
令
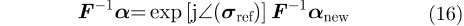
|
即
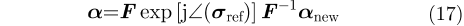
|
综合式(13)–式(17),可得
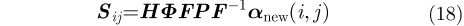
|
其中,
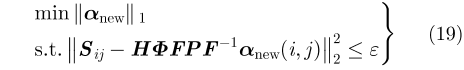
|
在所有距离向波数域
本文所用的柱面扫描人体安检成像实际数据由华讯方舟科技有限公司提供,由该公司研制的柱面扫描型毫米波3维成像人体安检系统,如图3所示。系统中阵列天线长度约2 m,在方位向上的扫描角约66°,天线辐射单元在方位向和高度向波束宽度约60°,其余参数如表1所示。测试目标为一高约2 m、宽约0.60 m的人体模特,模特手持一块高度约0.30 m、宽度约0.50 m的金属分辨率板,胸前粘有金属细条。
| 表 1 系统参数 Tab.1 System parameters |

|
图 3 柱面扫描型成像系统和测试目标 Fig.3 The cylindrical scanning imaging system and testing objectives |
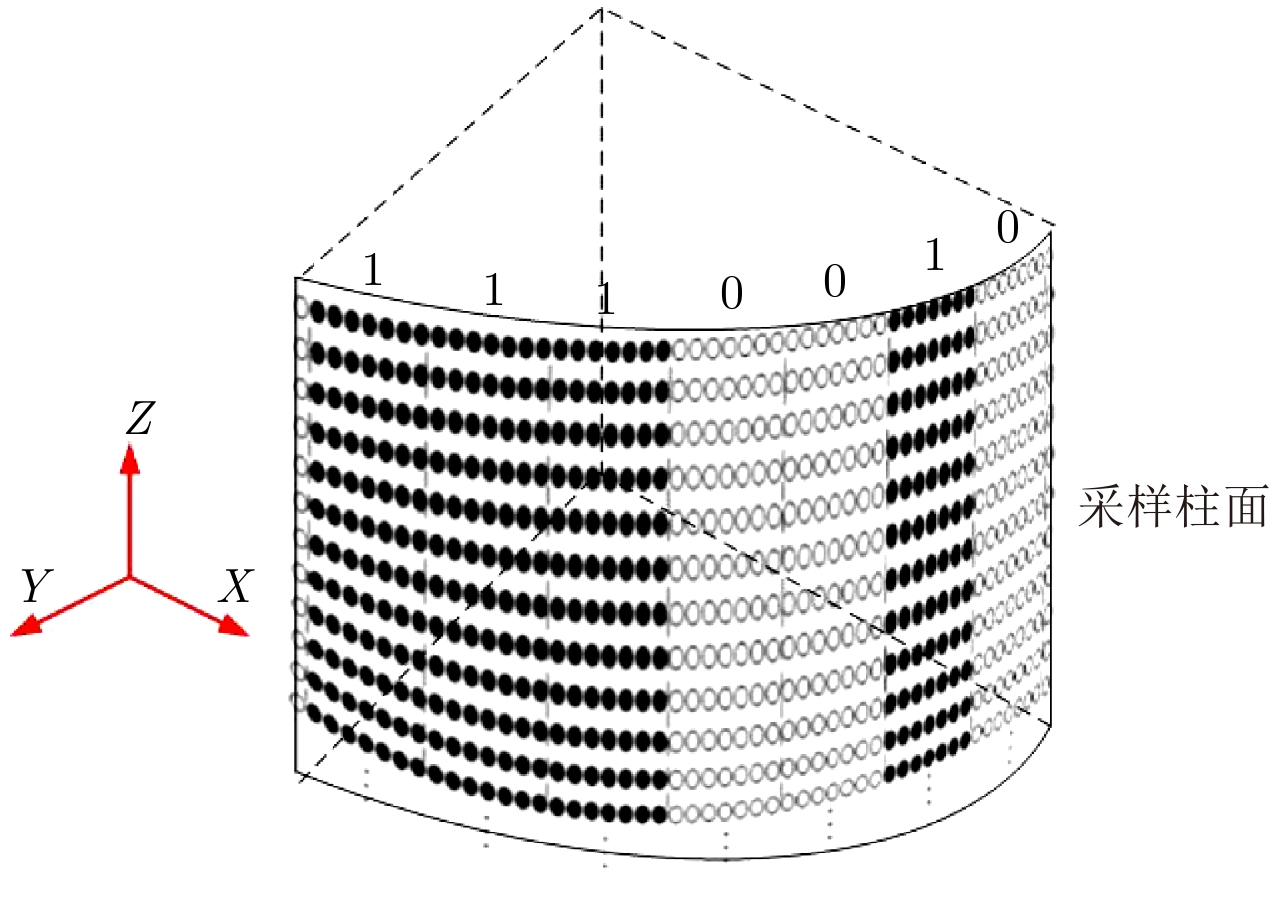
阵列天线以间隔da沿方位向均匀等间隔扫描,得到满采样数据;以扫描方向作为稀疏方向,采用长度分别为7, 11和13的巴克码伪随机序列作为稀疏采样准则,对满采样数据进行稀疏化(实际成像时可直接进行方位向稀疏扫描)。3种巴克码序列及性能如表2所示,基于7位巴克码的方位向稀疏采样示意图如图4所示,其中实心圆代表此处存在数据。
| 表 2 3种巴克码序列 Tab.2 The 3 kinds of Barker sequences |
|
图 4 柱面回波数据稀疏方式示意图 Fig.4 The sparse sampling method of cylindrical echo |
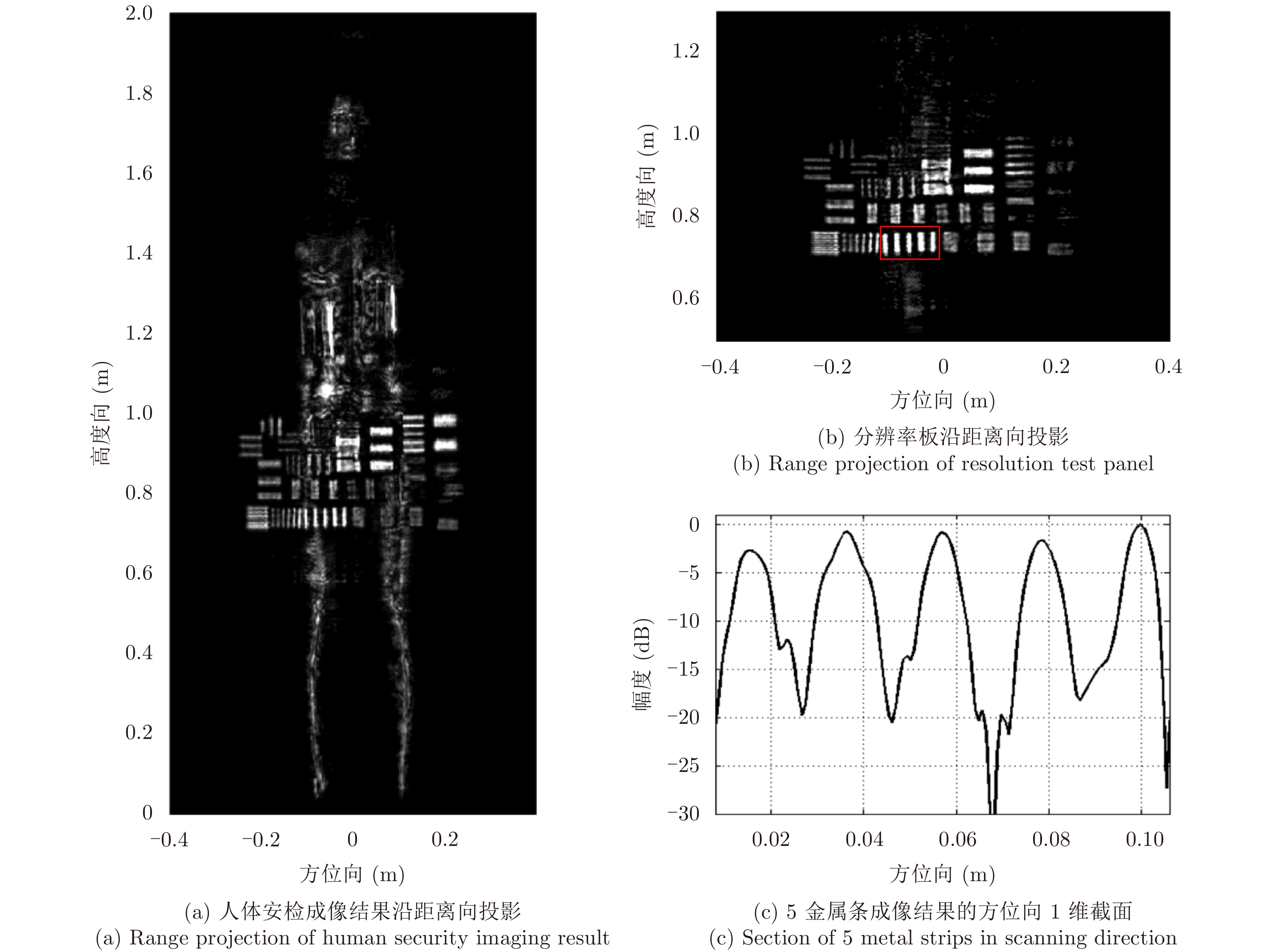
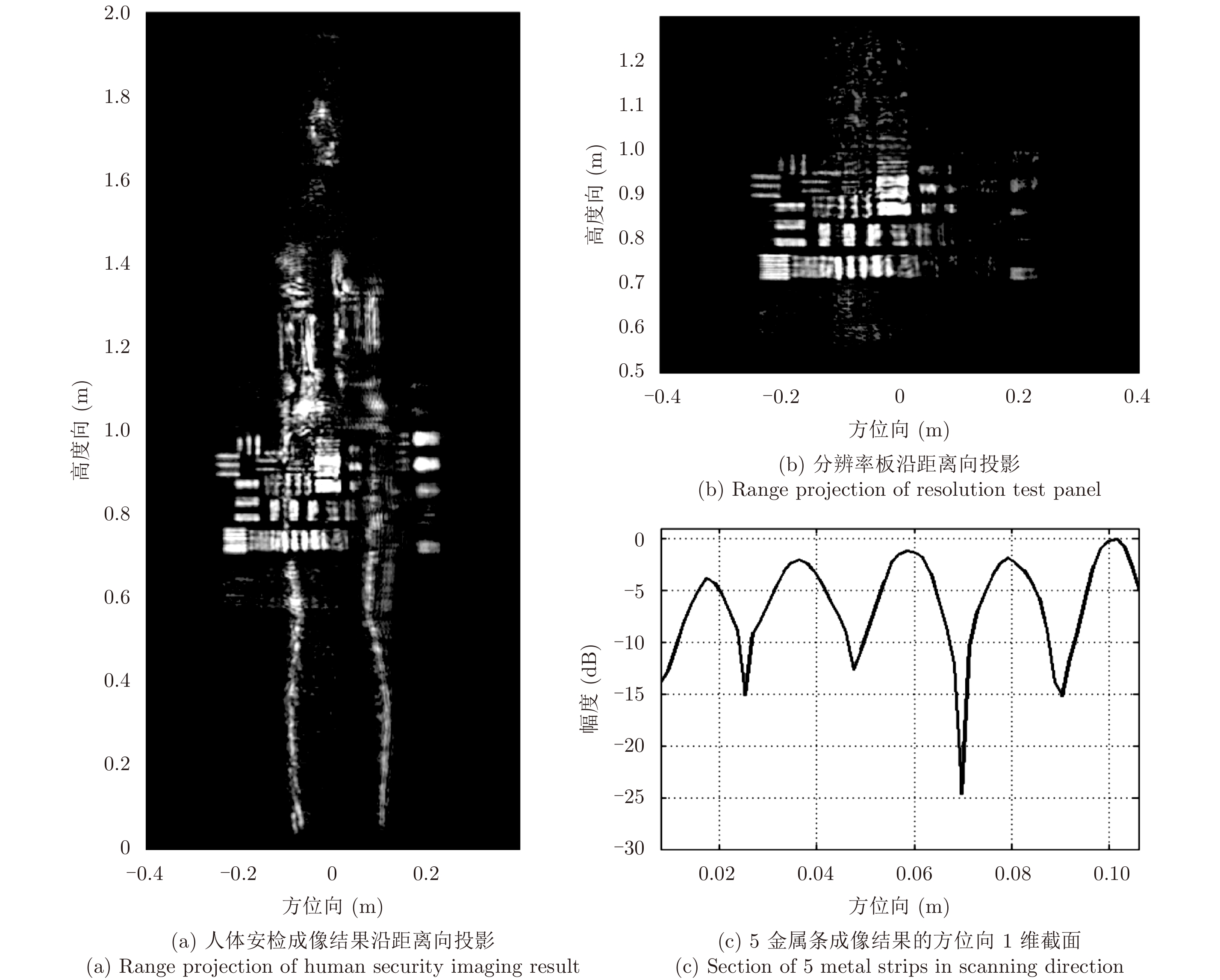
满采样实际数据的直接成像结果如图5所示,其中图5(a)为人体3维成像结果的距离向投影,图5(b)为其中金属分辨率板的距离向投影,图5(c)为图5(b)红色框中5个金属条在距离向–0.12 m、高度向0.74 m处的1维切面。从图中可清晰看到人体和金属条形状,红色方框内的5个金属条方位向尺寸约为5 mm,间隔2 cm;红框左侧的6个金属条方位向尺寸约为3 mm,间隔1 cm。
|
图 5 满采样条件下的人体安检直接成像结果 Fig.5 The direct imaging result under complete sampling |
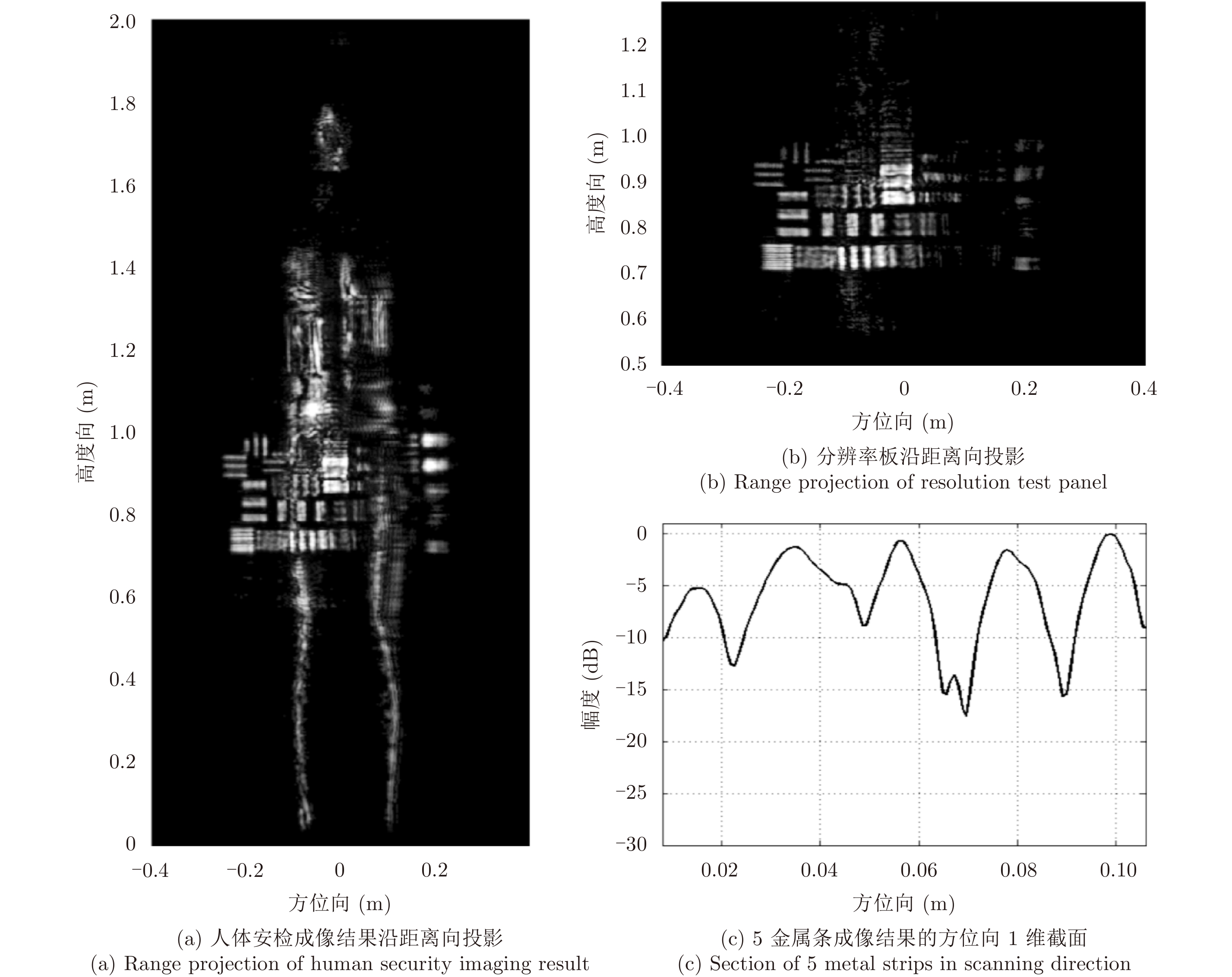
在扫描方向实施基于巴克码采样准则的稀疏采样,为了比较所提稀疏采样方法的有效性,本文同时采用等间隔稀疏采样方式。等间隔稀疏采样方式和基于7位巴克码准则的稀疏采样对应的直接成像结果分别如图6、图7所示。从图中可知,在等间隔稀疏采样方式下,图像方位向受栅瓣影响严重混叠,不能复原观测场景;在基于巴克码准则的稀疏采样下,图像无栅瓣影响,虽然方位向部分能量泄露至副瓣,但通过进一步的图像重建方法可恢复原始图像。

|
图 6 等间隔稀疏采样条件下的人体安检直接成像结果 Fig.6 The direct imaging result under uniformly spaced sparse sampling |
|
图 7 基于巴克码稀疏采样条件下的人体安检直接成像结果 Fig.7 The direct imaging result under Barker code sparse sampling |
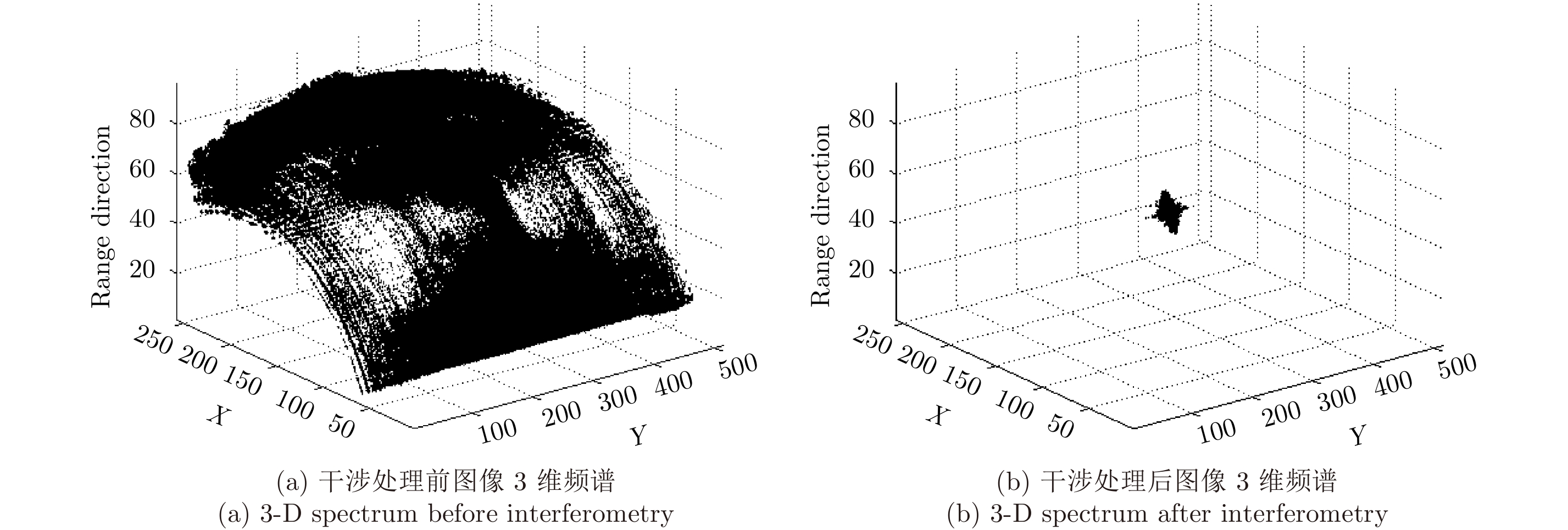
在基于巴克码准则的稀疏采样下,采用本文所提频域稀疏3维成像算法对稀疏采样信号的重建结果如图7–图8所示,其中参考图像由7位巴克码中前3位对应的部分满采样数据获得。从图中可知,经过原始图像信号和参考图像信号的干涉处理,图像信号3维频谱已压缩变窄(图8);对回波信号按照式(18)–式(19)进行频域CS稀疏重建,并将重建后的频谱逆变换至空间域,得到的成像结果没有高副瓣的现象,且分辨率接近满采样条件下的3维图像(图9)。
|
图 8 干涉处理前后图像3维频谱 Fig.8 The 3-D frequency spectrum before and after interferometry |
|
图 9 基于干涉处理和频域CS 3维成像算法的图像重建结果 Fig.9 The reconstruction of 3-D imaging algorithm based on interferometry and CS in frequency domain |
上述成像结果表明,基于干涉处理和频域CS的频域稀疏3维成像算法能够在稀疏采样条件下恢复目标场景,且图像具有与满采样相当的分辨率水平。为了定量分析所提方法在稀疏采样下的图像重建性能,本文将满采样对应的图像近似作为目标真值,采用均方根误差(Root Mean Square Error, RMSE)、相关系数和结构相似度[20](Structural SIMilarity, SSIM)3个指标对重建图像进行量化评价。均方根误差用来测量观测值和真值的偏差,定义为:
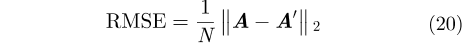
|
式中,A, A
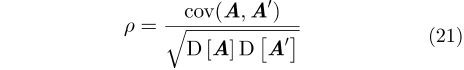
|
其中,
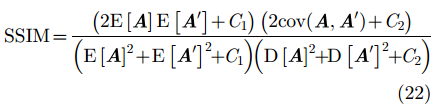
|
其中,C1, C2为用来维持稳定的常数。结构相似度取值范围为[–1, 1],两幅相同图像的结构相似度为1;两幅完全不相关图像的结构相似度为0;两幅完全相反的图像的结构相似度为–1。表3所示为基于7位巴克码准则稀疏采样条件下不同成像算法的图像重建性能评价结果。本文同时采用了长度为11和13的巴克码作为随机稀疏采样准则,对实际数据进行方位向稀疏化,并采用所提方法对稀疏回波数据进行图像重建;限于文章篇幅,仅列出不同长度巴克码稀疏采样下的图像质量评价结果(表4、表5)。从表中可知,在巴克码稀疏采样条件下,本文所提方法的重建图像接近满采样对应的成像效果,稀疏前后的图像相关系数大于0.9。
| 表 3 7位巴克码稀疏采样方式对应的图像质量评价 Tab.3 The image quality assessment corresponding to Barker code with length of 7 |
| 表 4 11位巴克码稀疏采样方式对应的图像质量评价 Tab.4 The image quality assessment corresponding to Barker code with length of 11 |
| 表 5 13位巴克码稀疏采样方式对应的图像质量评价 Tab.5 The image quality assessment corresponding to Barker code with length of 13 |
上述实际数据对应的成像系统基于柱面扫描3维成像模型,为减少数据采集量,增加安检成像通过速率,可采用基于实孔径平面阵列的毫米波快速成像系统。传统实孔径平面阵列为满足均匀半波长(
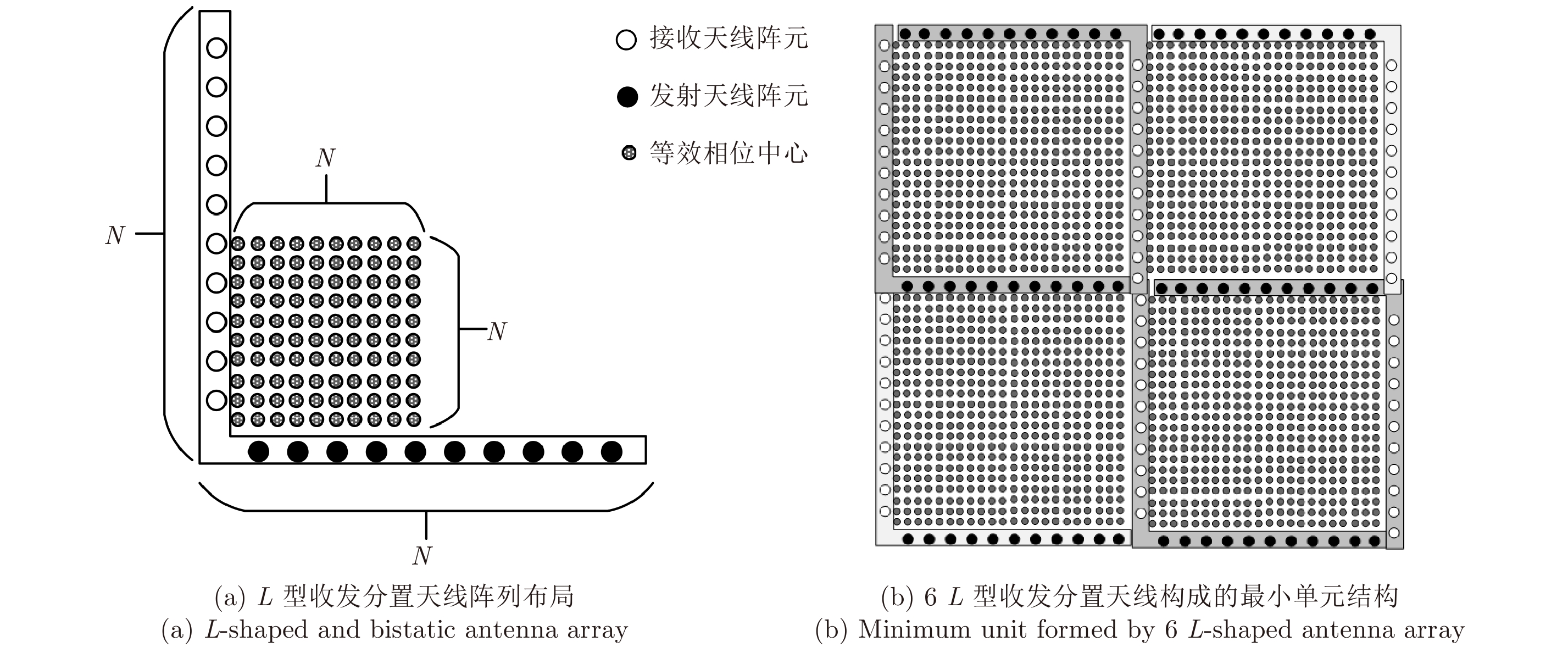
基于频域稀疏成像方法、巴克码稀疏采样方式和收发分置工作模式,设计用于快速安检成像的稀疏阵列布局,其中阵列最小单元为6个L型天线阵列组成的正方形结构[21],如图10所示。图10(a)为一个L型收发分置天线阵列布局示意图,接收、发射天线阵元个数均为N,阵元间隔为d,在多发多收条件下共产生N×N个间隔为d/2的等效相位中心;图10(b)为阵列最小单元结构示意图,包含6个收发分置的L型天线阵列,在系统多发多收工作模式下产生满采样分布的等效相位中心。
|
图 10 2维稀疏阵列中最小单元结构示意图 Fig.10 The structure of minimum unit in 2-D sparse array |
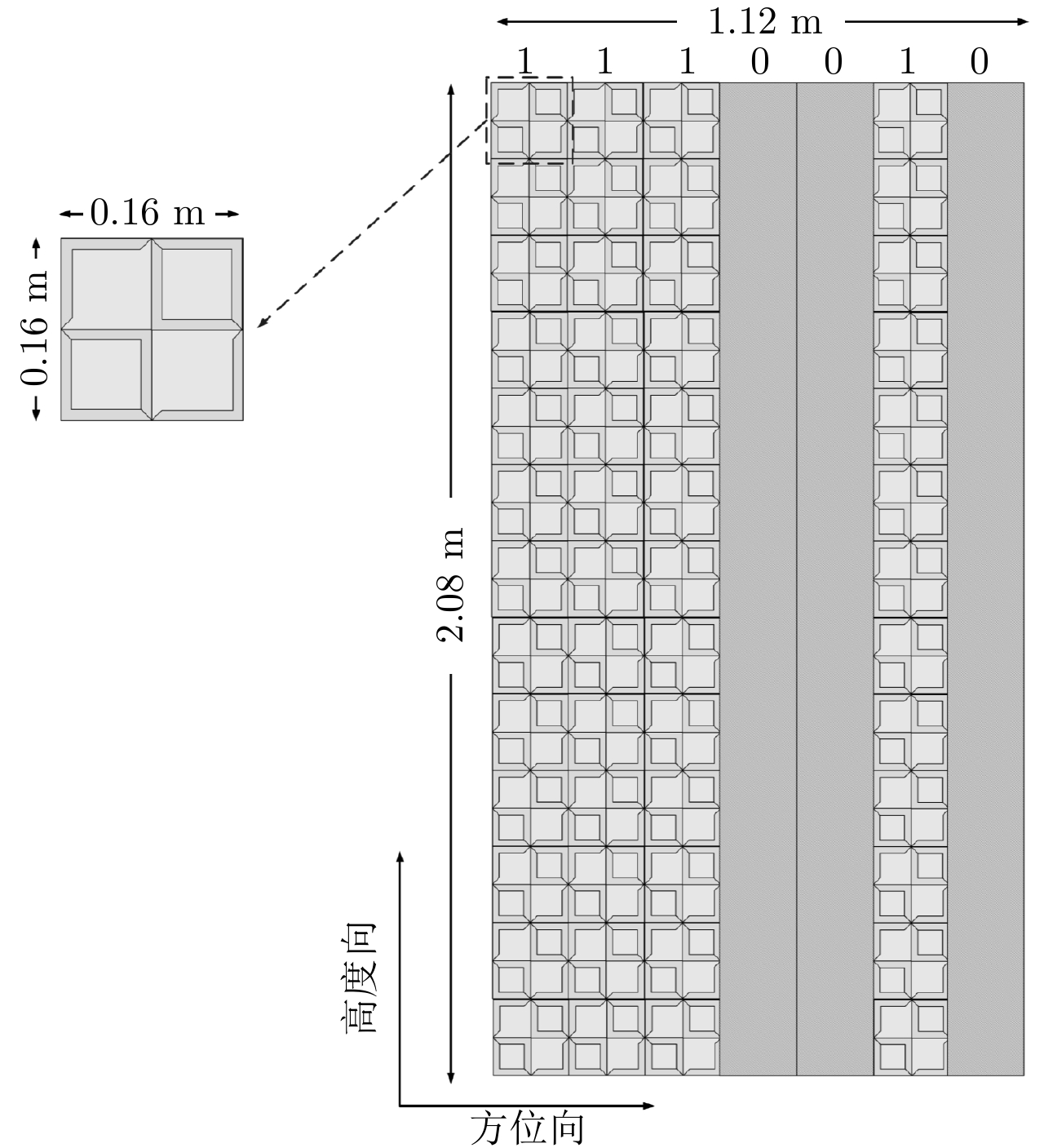
基于图10所示最小结构,假设雷达工作波长
|
图 11 毫米波快速成像2维稀疏阵列布局示意图 Fig.11 The 2-D sparse array structure for millimeter wave fast imaging |
本节对上述用于毫米波快速成像的平面稀疏阵列的主要性能指标进行分析。
(1) 成像分辨率
假设场景中心到平面阵列的测试距离为R0,阵列平面大小为
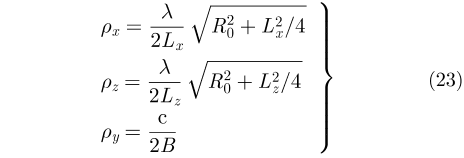
|
其中,
(2) 稀疏度
设稀疏阵列的物理辐射单元个数为N,稀疏阵列天线形成的等效相位中心均匀分布时所对应的空间位置个数为M,则稀疏阵列的稀疏率为:
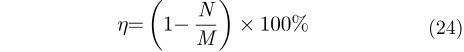
|
当采用如图10所示的稀疏阵列和上述成像参数时,稀疏阵列的稀疏率约为94.6%。
6 结论本文提出了一种基于巴克码准则的稀疏采样方式以降低柱面扫描安检系统的信号采集时间。在稀疏采样条件下,提出一种基于干涉处理和频域CS的频域稀疏3维成像算法。利用干涉处理使复图像频谱具备稀疏性,在频域建立柱面3维成像CS模型,并对稀疏后的回波进行图像重建。实际数据处理结果表明:本文所提方法在数据采集量减少约50%的条件下,仍可获得接近满采样的图像分辨率和成像效果,稀疏采样前后的图像相关系数优于0.9,在大人流量场所安全检测中具有重要应用价值和广阔市场前景。
为减少扫描采样时间,增加安检成像通过速率,减少辐射单元数量和系统复杂度,本文设计了基于频域稀疏成像方法和巴克码稀疏采样方式的毫米波快速成像稀疏阵列布局,在收发分置工作模式下实现了人体实时安检成像。在保证成像质量的前提下,该2维稀疏阵列的稀疏率高达94.6%,对今后的安检成像系统具有重要意义。
致谢 本文研究工作得到国家自然科学基金(项目批准号:61271422)项目资助;本文所用的柱面扫描人体安检成像实际数据由华讯方舟科技有限公司提供。由华讯方舟科技有限公司研制的柱面扫描型毫米波3维成像人体安检系统的研制工作得到深圳市科技创新委员会(Science, Technology and Innovation Commission of Shenzhen Municipality, No.JSGG20160229114231872)和深圳市发展和改革委员会(Development and Reform Commission of Shenzhen Municipality Government, No. [2016]1588)项目资助。在此表示感谢。
| [1] |
McMillan R W, Currie N C, Ferris D D, et al.. Concealed weapon detection using microwave and millimeter wave sensors[C]. Proceedings of 1998 International Conference on Microwave and Millimeter Wave Technology Proceedings, Beijing, 1998: 1–4. DOI: 10.1109/ICMMT.1998.768213.
( 0) 0)
|
| [2] |
温鑫, 黄培康, 年丰, 等. 主动式毫米波近距离圆柱扫描三维成像系统[J].
系统工程与电子技术, 2014, 36(6): 1044-1049. Wen Xin, Huang Pei-kang, Nian Feng, et al. Active millimeter-wave near-field cylindrical scanning three-dimensional imaging system[J]. Systems Engineering and Electronics, 2014, 36(6): 1044-1049. DOI:10.3969/j.issn.1001-506X.2014.06.05 (  0) 0)
|
| [3] |
Farhat N H and Guard W R. Millimeter wave holographic imaging of concealed weapons[J].
Proceedings of the IEEE, 1971, 59(9): 1383-1384. DOI:10.1109/PROC.1971.8441 ( 0) 0)
|
| [4] |
Gomez-Maqueda I, Almorox-Gonzalez P, Callejero-Andres C, et al. A millimeter-wave imager using an illuminating source[J].
IEEE Microwave Magazine, 2013, 14(4): 132-138. DOI:10.1109/MMM.2013.2248652 ( 0) 0)
|
| [5] |
Ahmed S S, Genghammer A, Schiessl A, et al. Fully electronic E-band personnel imager of 2 m2 aperture based on a multistatic architecture
[J].
IEEE Transactions on Microwave Theory and Techniques, 2013, 61(1): 651-657. DOI:10.1109/TMTT.2012.2228221 ( 0) 0)
|
| [6] |
Ahmed S S, Genghammer A, Schiessl A, et al.. Fully electronic active E-band personnel imager with 2 m2 aperture[C]. Proceedings of 2012 IEEE MTT-S International Microwave Symposium Digest, Montreal, QC, Canada, 2012: 1–3. DOI: 10.1109/MWSYM.2012.6259549.
( 0) 0)
|
| [7] |
Li L C, Li D J, and Pan Z H. Compressed sensing application in interferometric synthetic aperture radar[J].
Science China Information Sciences, 2017, 60(10): 102305 DOI:10.1007/s11432-016-9017-6 ( 0) 0)
|
| [8] |
Tian H, Li D J, and Li L C. Simulation of signal reconstruction based sparse flight downward-looking 3D imaging SAR[C]. Proceedings of 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, 2015: 3762–3765. DOI: 10.1109/IGARSS.2015.7326642.
( 0) 0)
|
| [9] |
Holubnychyi A. Generalized binary barker sequences and their application to radar technology[C]. Proceedings of 2013 Signal Processing Symposium (SPS), Serock, 2013: 1–9. DOI: 10.1109/SPS.2013.6623610.
( 0) 0)
|
| [10] |
Detlefsen J, Dallinger A, and Schelkshorn S. Approaches to millimeter-wave imaging of humans[C]. Proceedings of the First European Radar Conference, Amsterdam, the Netherlands, 2004: 279–282.
( 0) 0)
|
| [11] |
Rosen P A, Hensley S, Joughin I R, et al. Synthetic aperture radar interferometry[J].
Proceedings of the IEEE, 2000, 88(3): 333-382. DOI:10.1109/5.838084 ( 0) 0)
|
| [12] |
Tian H and Li D J. Sparse flight array SAR downward-looking 3-D imaging based on compressed sensing[J].
IEEE Geoscience and Remote Sensing Letters, 2016, 13(10): 1395-1399. DOI:10.1109/LGRS.2016.2560238 ( 0) 0)
|
| [13] |
张清娟, 李道京, 李烈辰. 连续场景的稀疏阵列SAR侧视三维成像研究[J].
电子与信息学报, 2013, 35(5): 1097-1102. Zhang Qing-juan, Li Dao-jing, and Li Lie-chen. Research on continuous scene side-looking 3D imaging based on sparse array[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1097-1102. DOI:10.3724/SP.J.1146.2012.01136 (  0) 0)
|
| [14] |
田鹤, 李道京, 潘洁, 等. 基于修正均匀冗余阵列正反编码的稀疏阵列SAR下视三维成像处理[J].
电子与信息学报, 2017, 39(9): 2203-2211. Tian He, Li Dao-jing, Pan Jie, et al. Downward-looking 3D imaging processing of sparse array SAR based on modified uniformly redundant arrays positive and negative coding[J]. Journal of Electronics & Information Technology, 2017, 39(9): 2203-2211. DOI:10.11999/JEIT161209 (  0) 0)
|
| [15] |
李烈辰, 李道京. 基于压缩感知的连续场景稀疏阵列SAR三维成像[J].
电子与信息学报, 2014, 36(9): 2166-2172. Li Lie-chen and Li Dao-jing. Sparse array SAR 3D imaging for continuous scene based on compressed sensing[J]. Journal of Electronics & Information Technology, 2014, 36(9): 2166-2172. DOI:10.3724/SP.J.1146.2013.01645 (  0) 0)
|
| [16] |
Candès E and Romberg J. Sparsity and incoherence in compressive sampling[J].
Inverse Problems, 2007, 23(3): 969-985. DOI:10.1088/0266-5611/23/3/008 ( 0) 0)
|
| [17] |
Donoho D L. Compressed sensing[J].
IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 ( 0) 0)
|
| [18] |
Baraniuk R and Steeghs P. Compressive radar imaging[C]. Proceedings of 2007 IEEE Radar Conference, Boston, Mass, USA, 2007: 128–133. DOI: 10.1109/RADAR.2007.374203.
( 0) 0)
|
| [19] |
Patel V M, Easley G R, Healy jr D M, et al. Compressed synthetic aperture radar[J].
IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 244-254. DOI:10.1109/JSTSP.2009.2039181 ( 0) 0)
|
| [20] |
Tian H and Li D J. Sparse sampling-based microwave 3D imaging using interferometry and frequency-domain principal component analysis[J].
IET Radar, Sonar & Navigation, 2017, 11(12): 1886-1891. DOI:10.1049/iet-rsn.2017.0087 ( 0) 0)
|
| [21] |
Schiessl A, Ahmed S S, Genghammer A, et al.. A technology demonstrator for a 0.5 m x 0.5 m fully electronic digital beamforming mm-Wave imaging system[C]. Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, 2011: 2606–2609.
( 0) 0)
|
| [22] |
Tian H, Li D J, and Hu X. Microwave three-dimensional imaging under sparse sampling based on MURA code[C]. Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, 2016: 7411–7414. DOI: 10.1109/IGARSS.2016.7730933.
( 0) 0)
|




