② (东南大学毫米波国家重点实验室 南京 210096)
② (State Key Laboratory of Millimeter Waves, Southeast University, Nanjing 210096, China)
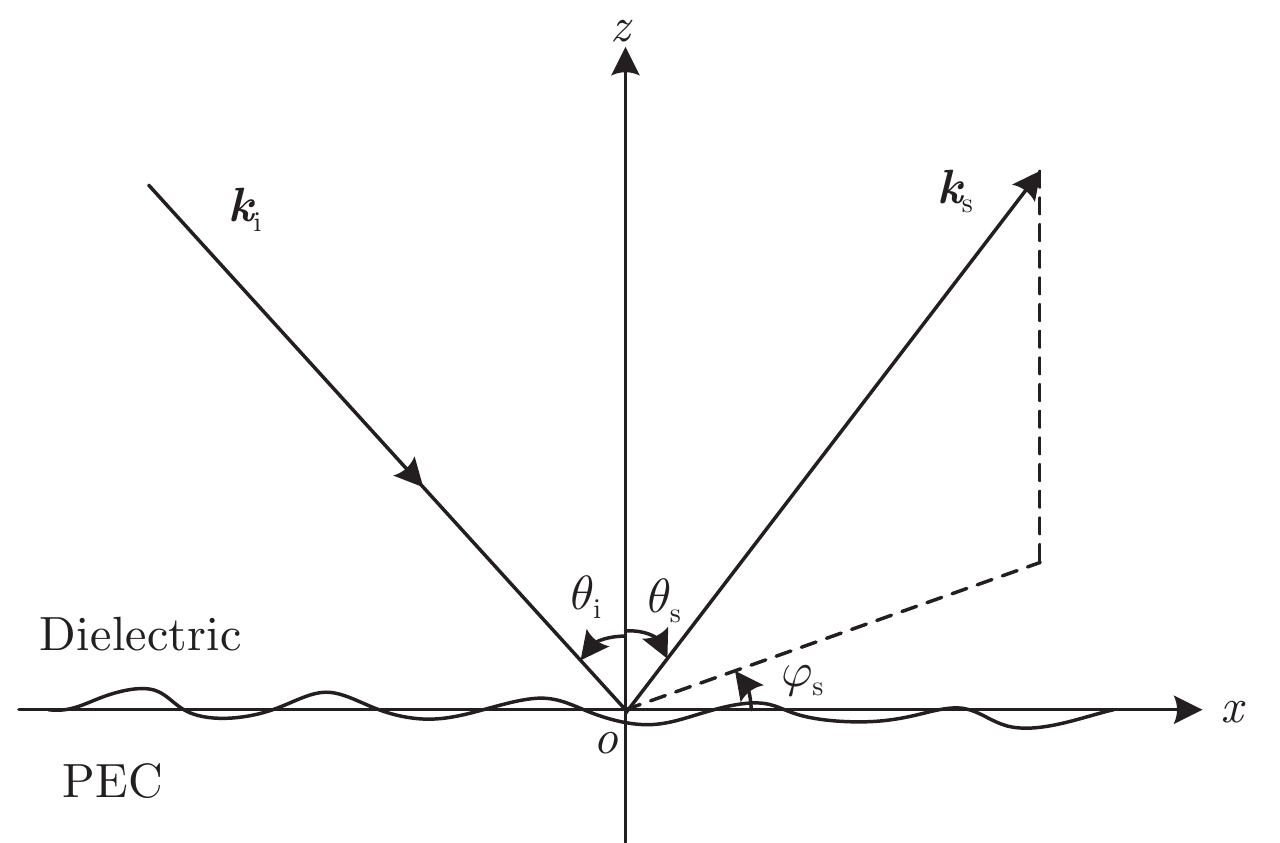
太赫兹波通常是指频率在0.1 THz到10 THz范围内的电磁波,位于微波和红外辐射之间。由于缺乏大功率的辐射源和高灵敏度的接收机,致使该频段仍有许多领域有待开发[1]。随着太赫兹雷达技术的发展[2,3],太赫兹雷达散射截面(Radar Cross Sections, RCS)越来越重要。物理光学法(Physical Optics, PO)结合截断劈增量长度绕射系数法(Truncated-wedge Incremental length Diffraction Coefficients, TWILDC)已被证实为能够高效计算光滑金属目标的RCS[4,5]。对于微粗糙表面,常用微扰法(Small Perturbation Method, SPM)研究微粗糙表面的散射。根据微波和红外激光散射理论,假设金属目标可以被看成具有微粗糙表面的理想导体(Perfectly Electric Conducting, PEC)。因此,太赫兹波段目标是散射分为相干部分和非相干部分[6–8]。其中,相干散射场利用微波散射理论求解而非相干散射场利用微粗糙面散射理论求解。
在计算电磁学领域,多层快速多极子算法(Multilevel Fast Multipole Algorithm, MLFMA)对目标的计算结果被认为是标准,等效于实验结果。然而,一般目标在太赫兹波段电尺寸非常巨大,MLFMA由于计算时间和计算机内存的限制,很少使用,近似算法则体现出计算速度的优势。在这样的背景下,需要寻找一个高效,准确的快速算法来研究太赫兹波段目标的散射问题。考虑到目前太赫兹雷达发射源功率水平、探测距离和高灵敏度接收技术,本文将发射频率聚焦于太赫兹低频段。首先假设在太赫兹低频段可以将金属目标看成是具有随机微粗糙表面物体,通过MLFMA计算比较同一微粗糙表面在30 GHz和300 GHz单站和双站RCS分布,数值证明了假设的有效性。接着,结合蒙特卡洛方法,提出采用PO+TWILDC+SPM混合近似算法研究了典型的具有微粗糙表面的无限薄金属板在太赫兹波段的散射特性,并与MLFMA比较验证了该混合算法的有效性。
2 微粗糙目标散射理论基于太赫兹介于微波和红外波段的特殊性,考虑边缘绕射的贡献,提出采用PO+TWILDC+SPM混合近似算法来计算典型的具有微粗糙表面无限薄金属板在太赫兹波段的散射分布。其中,SPM计算非相干散射分量RCS, PO+TWILDC结合粗糙面特征函数用来计算相干散射分量RCS,然后将相干和非相干散射分量混合叠加,得到总的RCS分布,即为PO+TWILDC+SPM混合近似算法的计算结果。
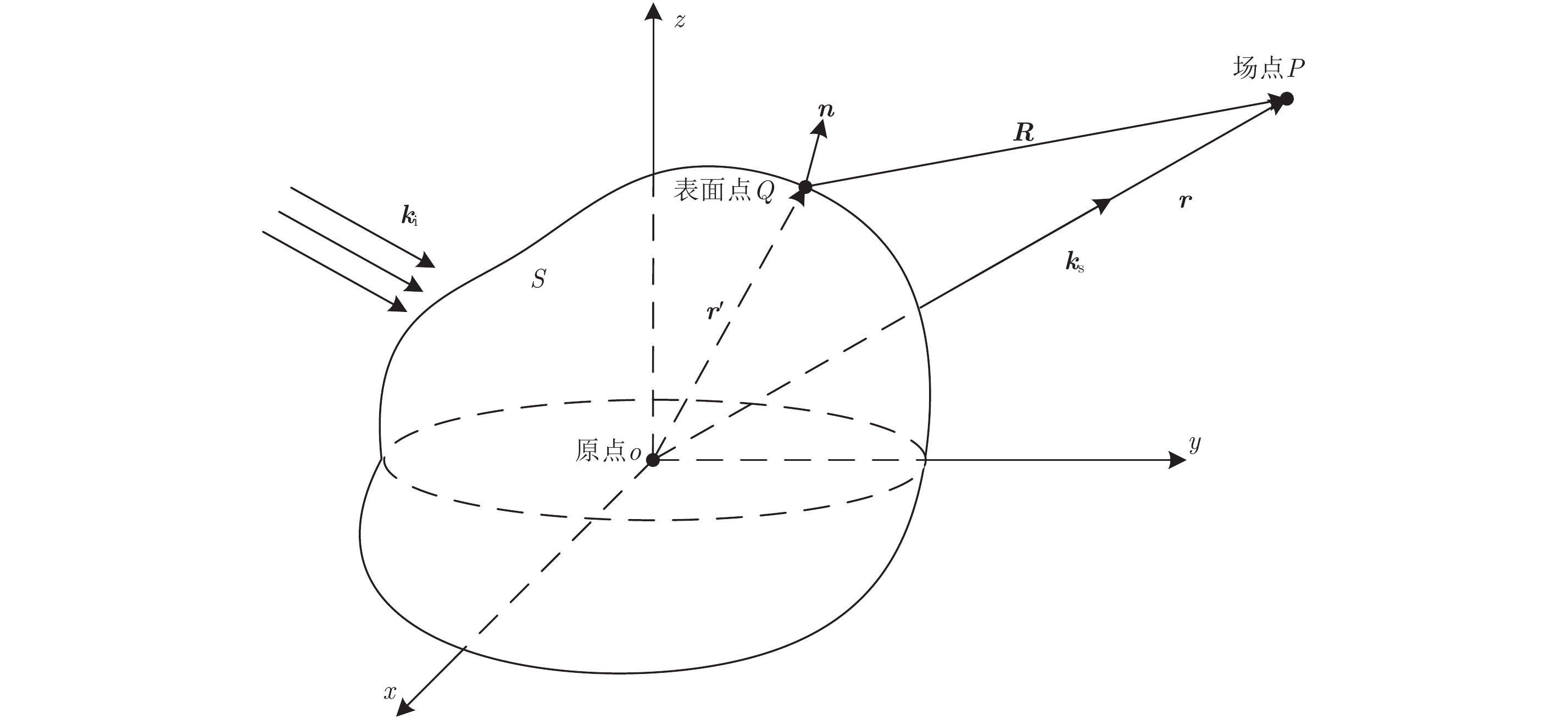
2.1 物理光学法考虑一个位于自由空间中的有限散射体,闭合表面为S,观察点P位于表面S之外,单位幅度的平面波入射,如图1所示。
|
图 1 PO散射示意图 Fig.1 Schematic diagram of the scattered field with PO method |
物理光学法通常被用于处理电大尺寸目标的电磁散射问题。其基本原理是:用散射体表面的感应电流JPO取代散射体本身,通过对表面感应场的近似和积分而求得物体的散射场[4]。
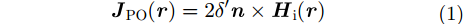
|
其中,n为表面外法向单位矢量,
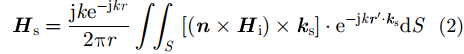
|
其中,Hs为散射磁场,r
当散射方向位于镜像点附件时,PO计算结果准确,但PO忽略了多次反射、边缘和尖劈的作用,当散射方向远离镜像点时,PO计算结果误差较大。因此,为减少散射方向远离镜像点时的散射损失,本文采用TWILDC计算来自边缘、尖顶和拐角散射场贡献[9]。
2.2 随机导体粗糙面相干散射RCS如图2所示,微粗糙PEC目标表面散射可以分为相干散射和非相干散射两部分:
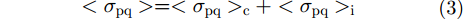
|
其中,<
|
图 2 粗糙表面散射示意图 Fig.2 Schematic diagram of rough surface scattering |
如果微粗糙表面的高度起伏同时与表面斜度起伏无关,则可以利用切平面近似和稳定相位法,得到粗糙PEC目标表面相干散射截面<
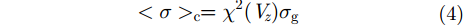
|
其中,k0为波数,
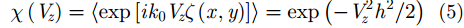
|
V=ki–ks, Vz是V沿着z方向的分量。h是表面高度起伏均方根。
2.3 随机导体粗糙面非相干散射RCS利用切平面近似,将物体表面分割成一系列几何单元,根据粗糙面电磁散射理论,得到各单元面积非相干散射截面。在高频近似下,可近似认为各单元面的非相干散射彼此不相关。因此,物体总的非相干散射截面是各单元面非相干散射截面之和[10],即
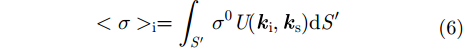
|
式中,U(ki, ks)为遮蔽函数,表示积分只在入射波能照射曲面上,同时观察方向亦能看到的区域进行。对于阴影区域U(ki, ks)=0,对于可照射区域,U(ki, ks)=1。
如图2所示,当粗糙表面的高度起伏均方根h和相关长度 l 满足式(7),可以使用微扰法计算微粗糙表面的非相干散射[8]。
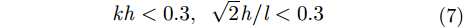
|
平面波入射至微粗糙PEC表面,根据微扰法可以获得非相干散射系数表达式为:
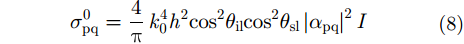
|
其中,(
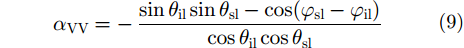
|
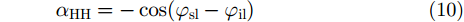
|
I 的表达式为:
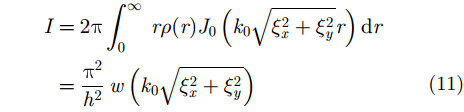
|
其中,
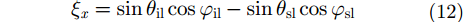
|
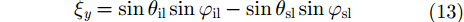
|
其中,w(u)为微粗糙表面的粗糙度密度函数;J0(x)为零阶柱贝塞尔函数;
高斯粗糙面的相关系数
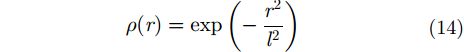
|
因此,I 的表达式具体为:
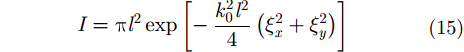
|
随机粗糙表面可以看成是一个平稳随机过程,其样本的产生可以采用经典的谱FFT方法。主要原理:先产生一个高斯白噪声,然后利用粗糙表面功率谱密度对高斯白噪声进行滤波,最后再做一个FFT生成随机粗糙表面的高度值[11]。基于这种方法,生成了一组满足基尔霍夫近似的具有相同粗糙度参数的高斯随机微粗糙表面。假设入射波波长为
|
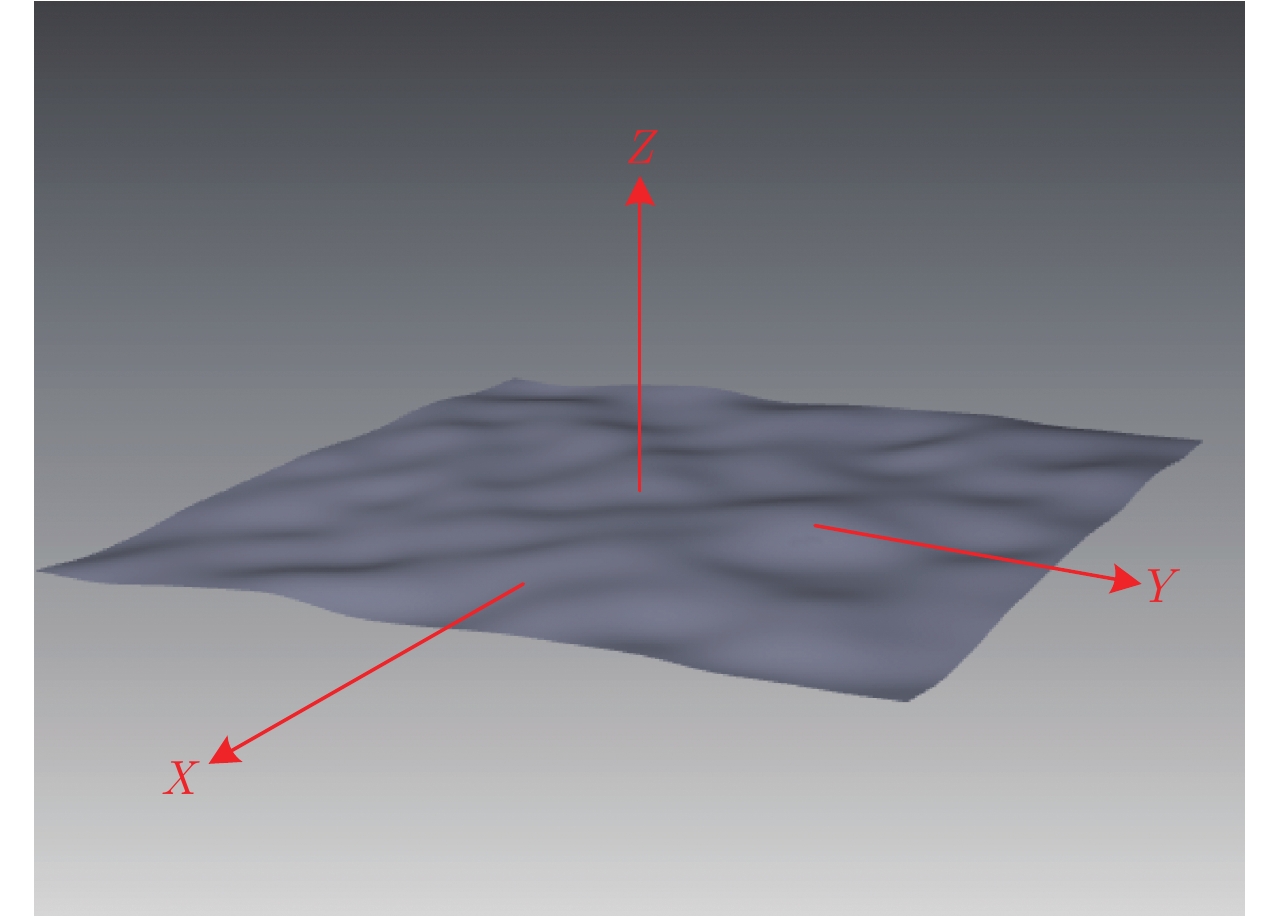
图 3 无限薄粗糙平板示意图 Fig.3 Schematic diagram of an infinitely thin rough PEC plate |
本节假设在太赫兹频段金属目标可以被视为具有微粗糙表面的PEC目标,接着基于MLFMA方法分别计算并比较在30 GHz和300 GHz频段微粗糙面和对应光滑表面的单站和双站RCS,结果表明,粗糙度对于RCS有很大的影响,因此在太赫兹波段金属目标可以被视为具有微粗糙起伏的PEC目标。最后,提出采用PO+TWILDC+SPM混合算法计算无限薄平板RCS分布,其中,PO+TWILDC计算相干散射RCS, SPM计算非相干散射RCS。
如图3所示为一无限薄微粗糙理想导体平板,其大小为10 mm×10 mm。粗糙表面的粗糙度参数为
|
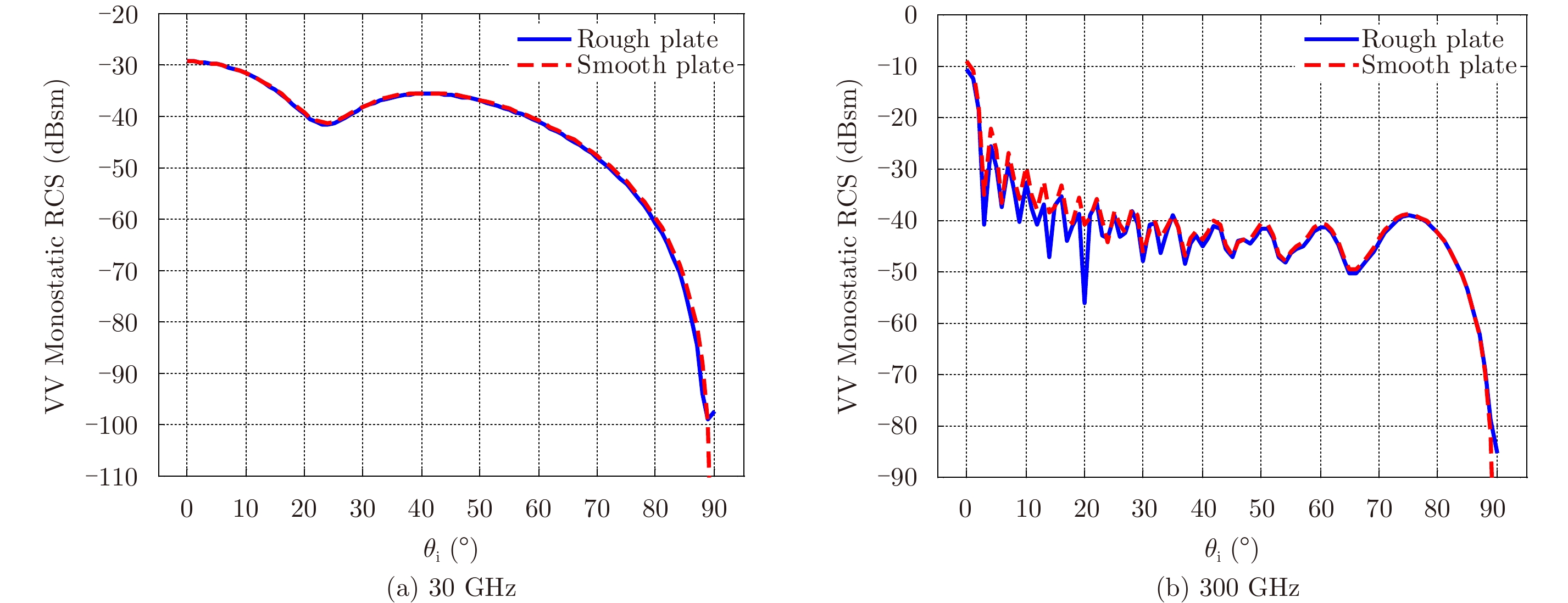
图 4 无限薄平板单站VV极化MLFMA计算RCS分布 Fig.4 Monostatic VV-polarization RCS of the infinitely thin PEC plate by MLFMA algorithm |
图4(a)和图4(b)为在30 GHz和300 GHz利用MLFMA计算粗糙无限薄PEC平板和对应相同尺寸光滑平板的单站RCS结果比较。从图4(a)可以看出除了90°附近外,两种结果吻合很好。图4(b)可以看出在0°到23°范围内,两种结果不一致,随着入射角度的增大,两种结果吻合很好,这可以由Fraunhofer判据解释,该判据指出如果粗糙表面上两点反射程差的相位差小于
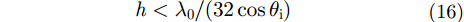
|
则表面是光滑的,否则是粗糙的。其中,
在图4(a)中,f=30 GHz,
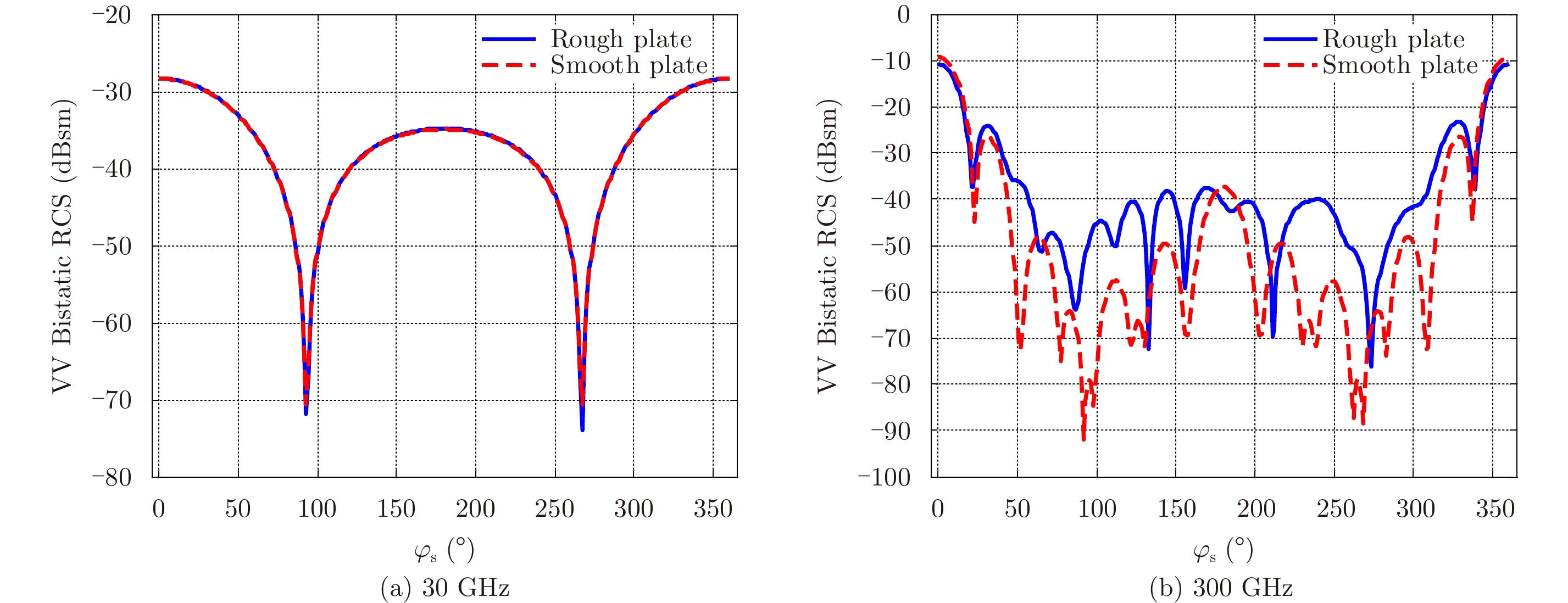
图5(a)和图5(b)为30 GHz和300 GHz利用MLFMA计算无限薄微粗糙PEC平板和对应相同尺寸大小的光滑平板的双站RCS结果比较,其中实线均表示粗糙平板计算结果,虚线均表示对应的光滑平板结果。图5(a)中可以看到两条曲线吻合很好,图5(b)中可以看到两条曲线相差较大,其中在0°和360°附近,也就是镜向附近,对应的RCS相差了1.5 dBsm,而在其它方向上,相差更大,说明了在300 GHz粗糙度的影响较大。比较图4和图5,可以看出在微波波段,大部分目标表面可以被看成是光滑表面,而随着频率的增大,表面起伏开始出现影响,进入太赫兹波段,可以认为目标表面是具有微粗糙起伏的表面。
|
图 5 无限薄平板双站VV极化MLFMA计算RCS分布 Fig.5 Bistatic VV-polarization RCS of the infinitely thin PEC plateby MLFMA algorithm |
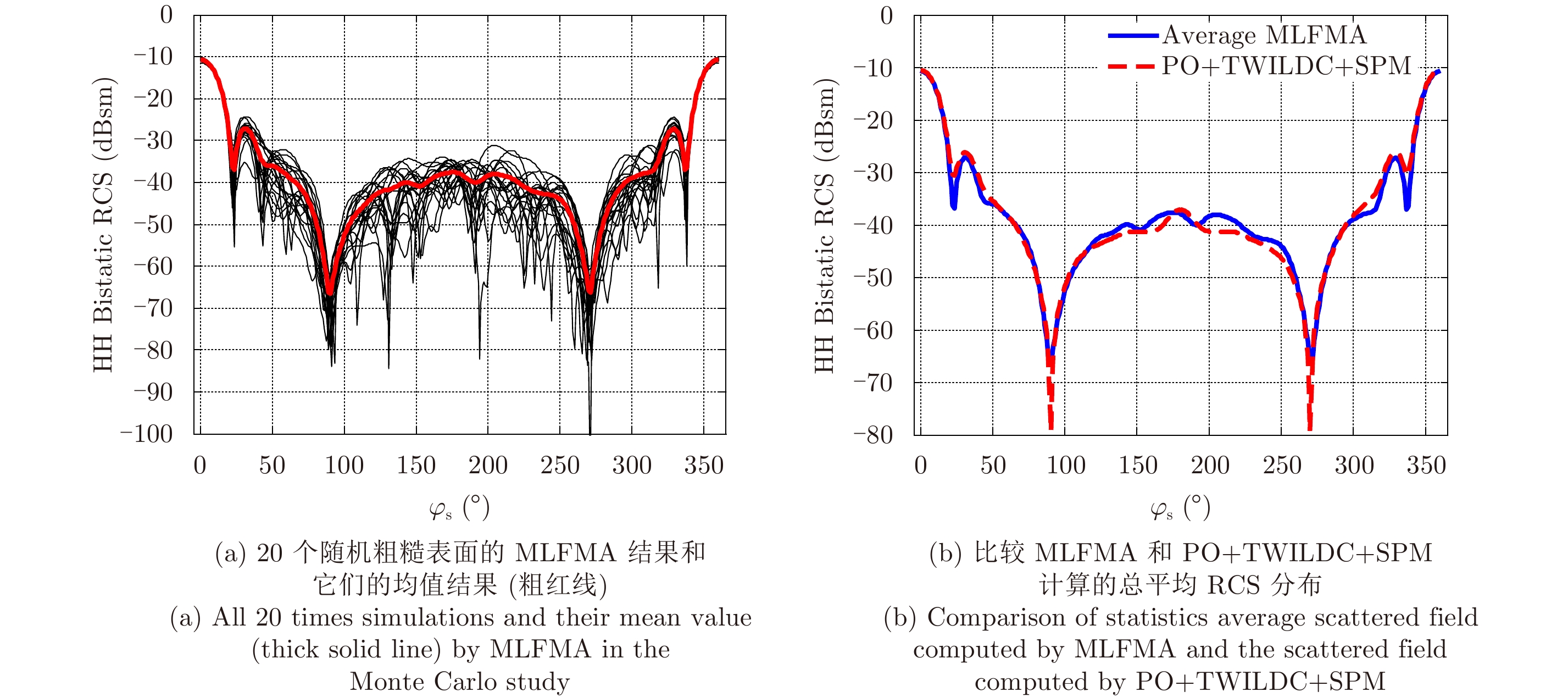
由于粗糙表面的生成具有随机性,采用蒙特卡洛方法来研究目标在太赫兹波段的散射特性。主要实现过程可以简化为:(1)利用计算机产生大量的具有相同粗糙度统计特征的随机表面,它们具有不同的轮廓代表不同的可能起伏;(2)根据MLFMA分别计算每个随机表面的散射分布;(3)考虑所有的表面分布得到的所有散射场RCS的均值来代表总的平均结果。
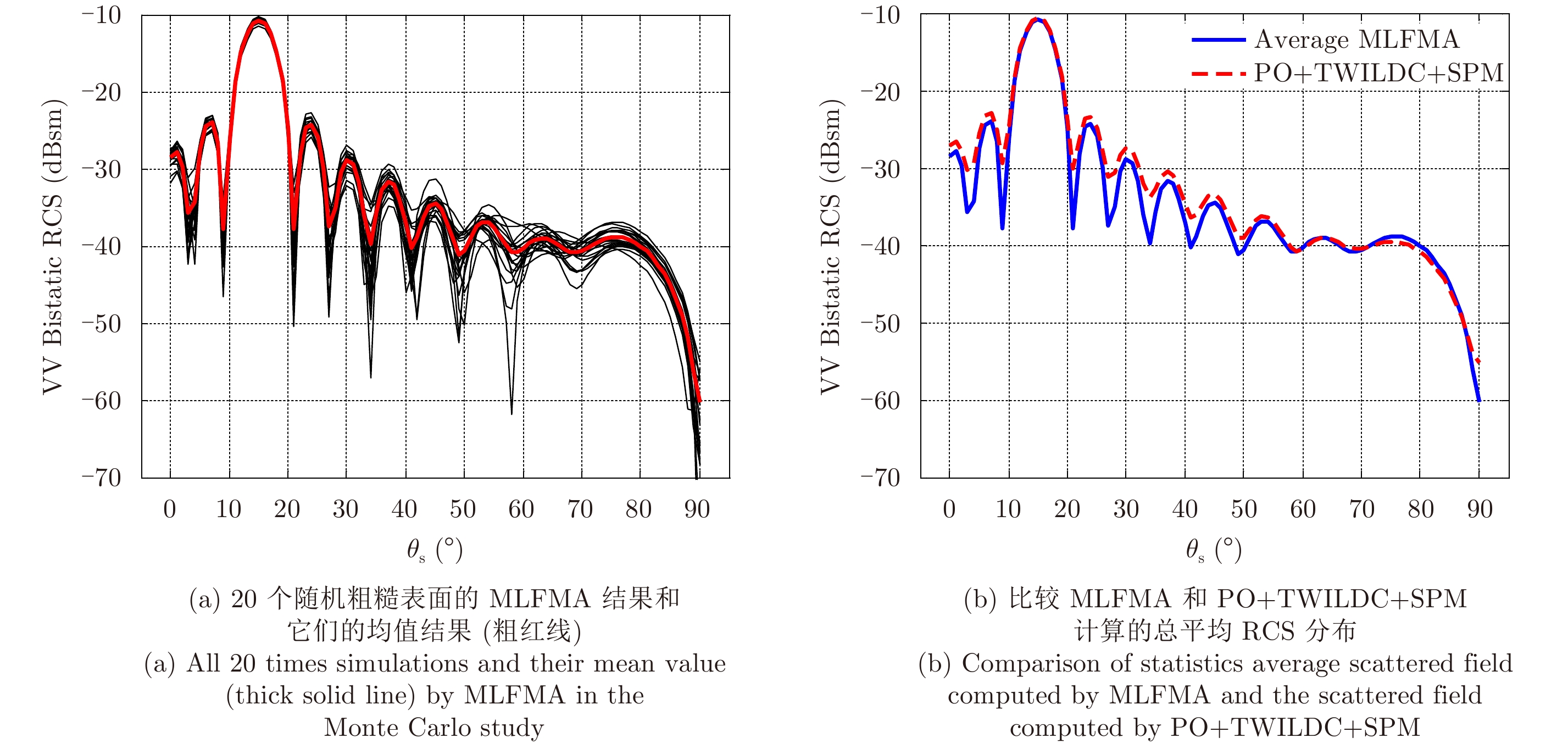
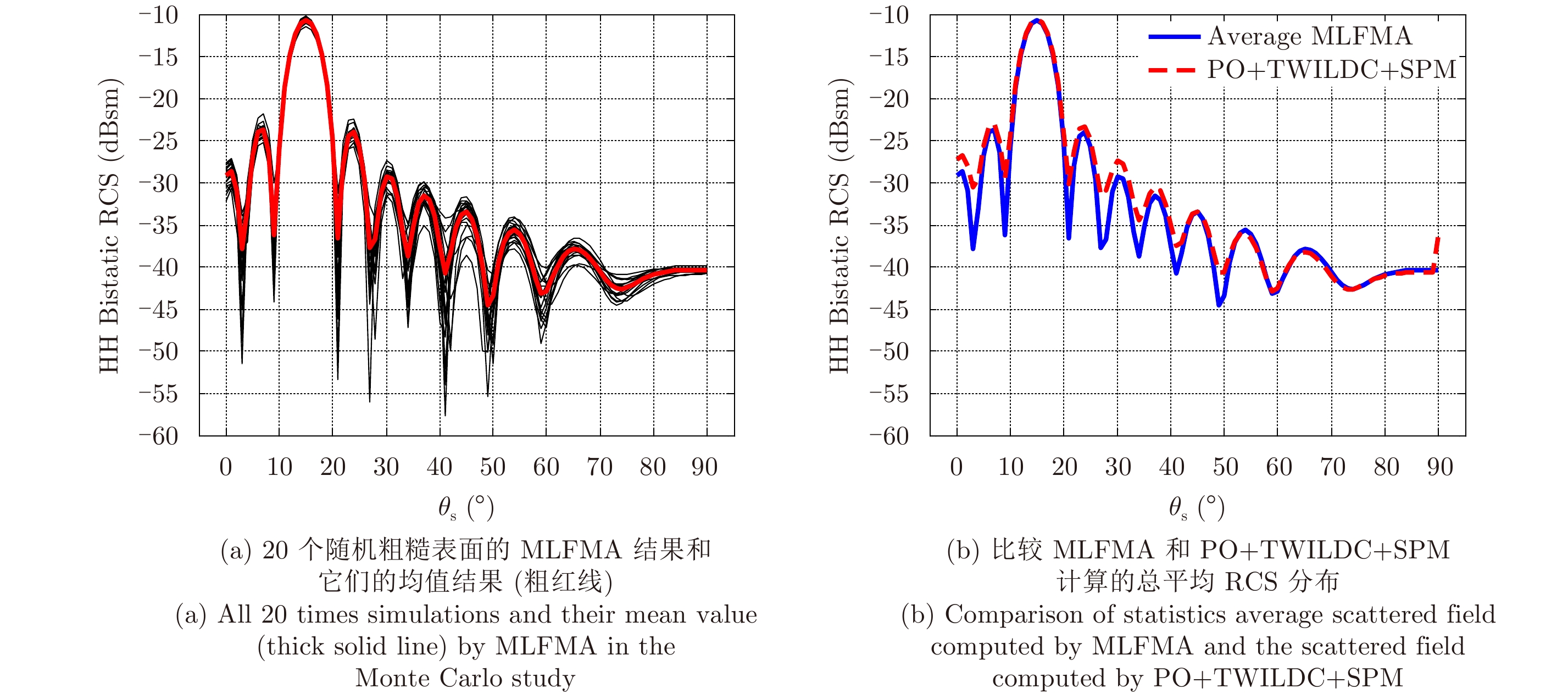
基于蒙特卡洛方法,图6(a)–图9(a)利用MLFMA计算20次随机粗糙表面VV和HH双站极化RCS结果以及它们的均值结果(粗实线)。图6(b)–图9(b)比较了利用MLFMA计算总的平均场(实线)和利用PO+TWILDC+SPM计算的散射RCS的VV和HH极化结果(虚线)。从图6(b)和图7(b)可以看出两条曲线的峰值和随散射俯仰角的变化趋势吻合很好,特别地,在
|
图 6 双站VV极化RCS结果分布(300 GHz)。角度设置为
|
|
图 7 双站HH极化RCS结果分布(300 GHz)。角度设置为
|
|
图 8 双站VV极化RCS结果分布(300 GHz)。角度设置为
|
|
图 9 双站HH极化RCS结果分布(300 GHz)。角度设置为
|
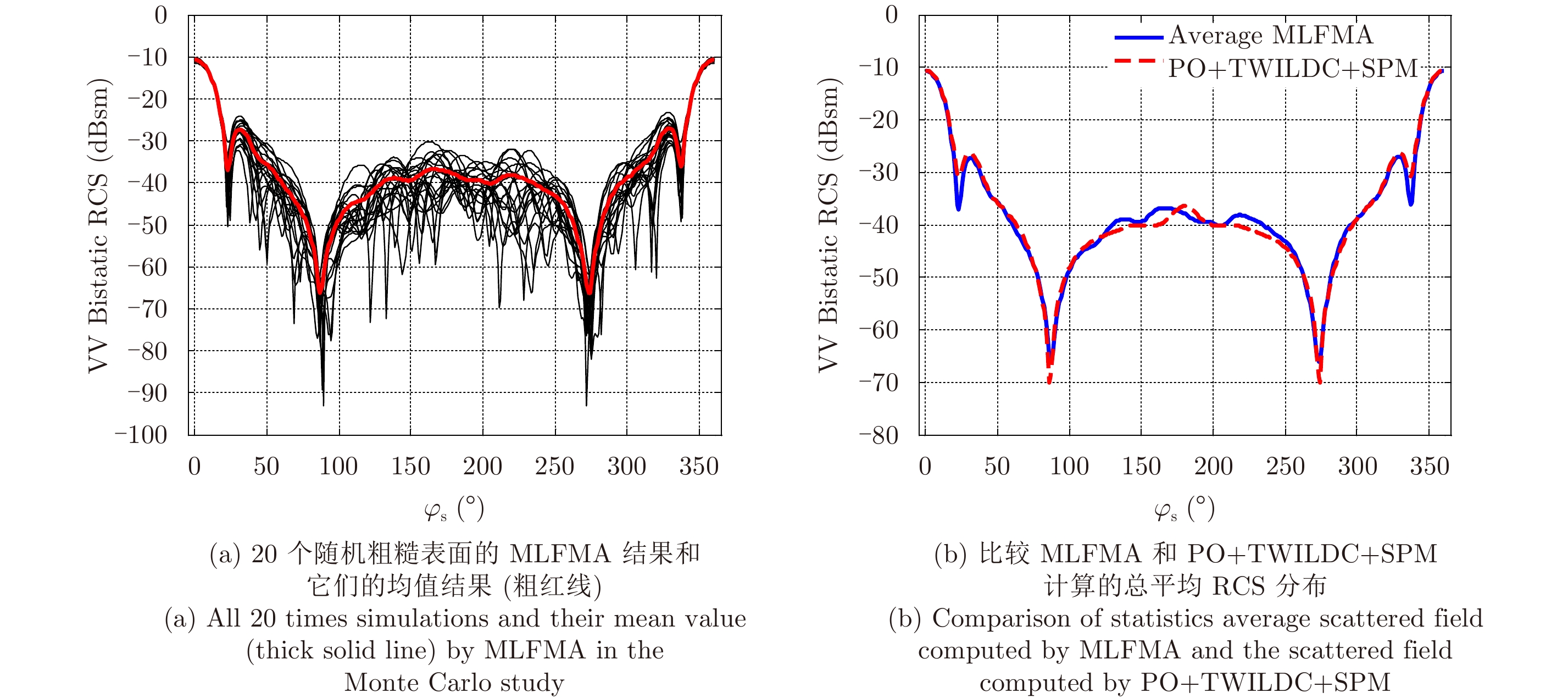
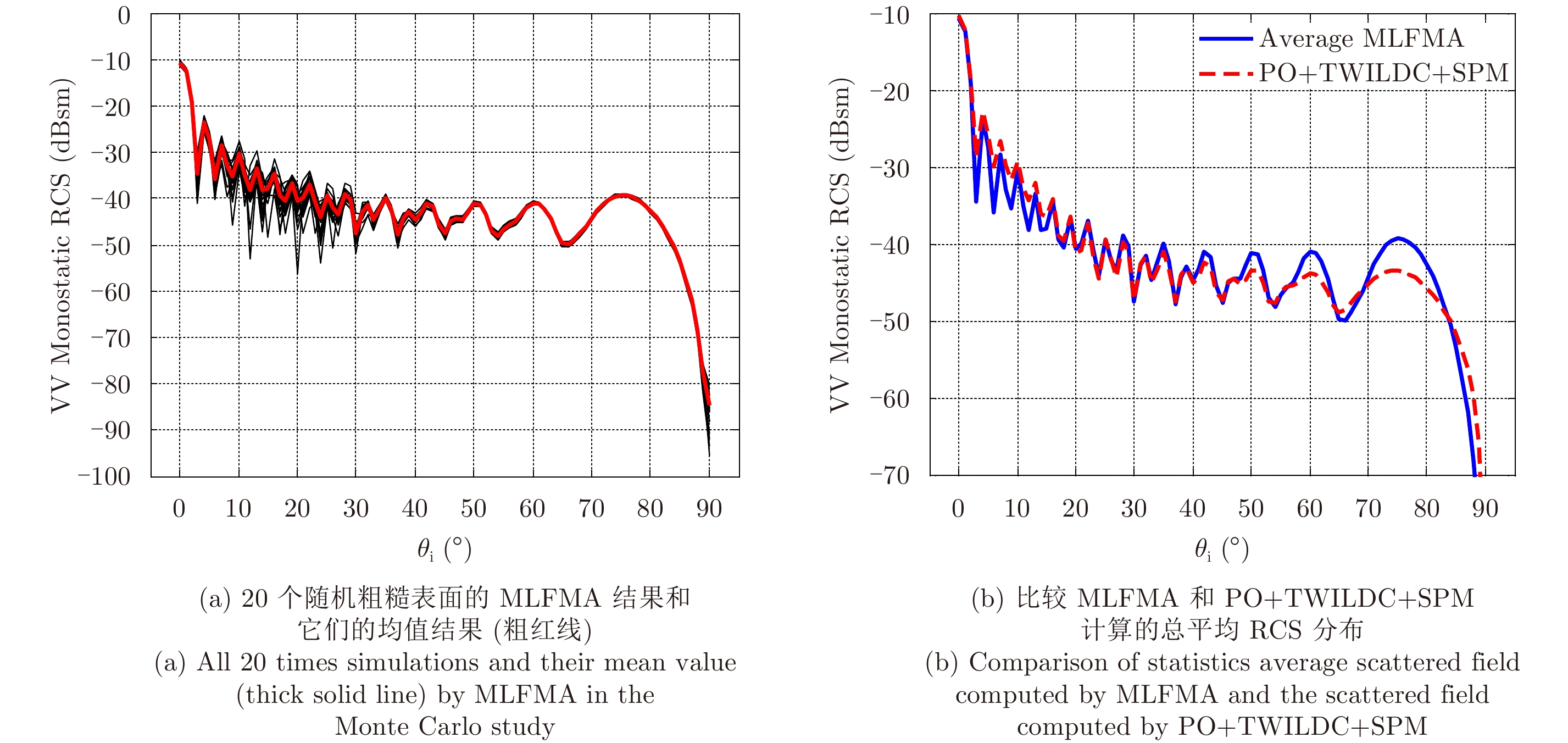
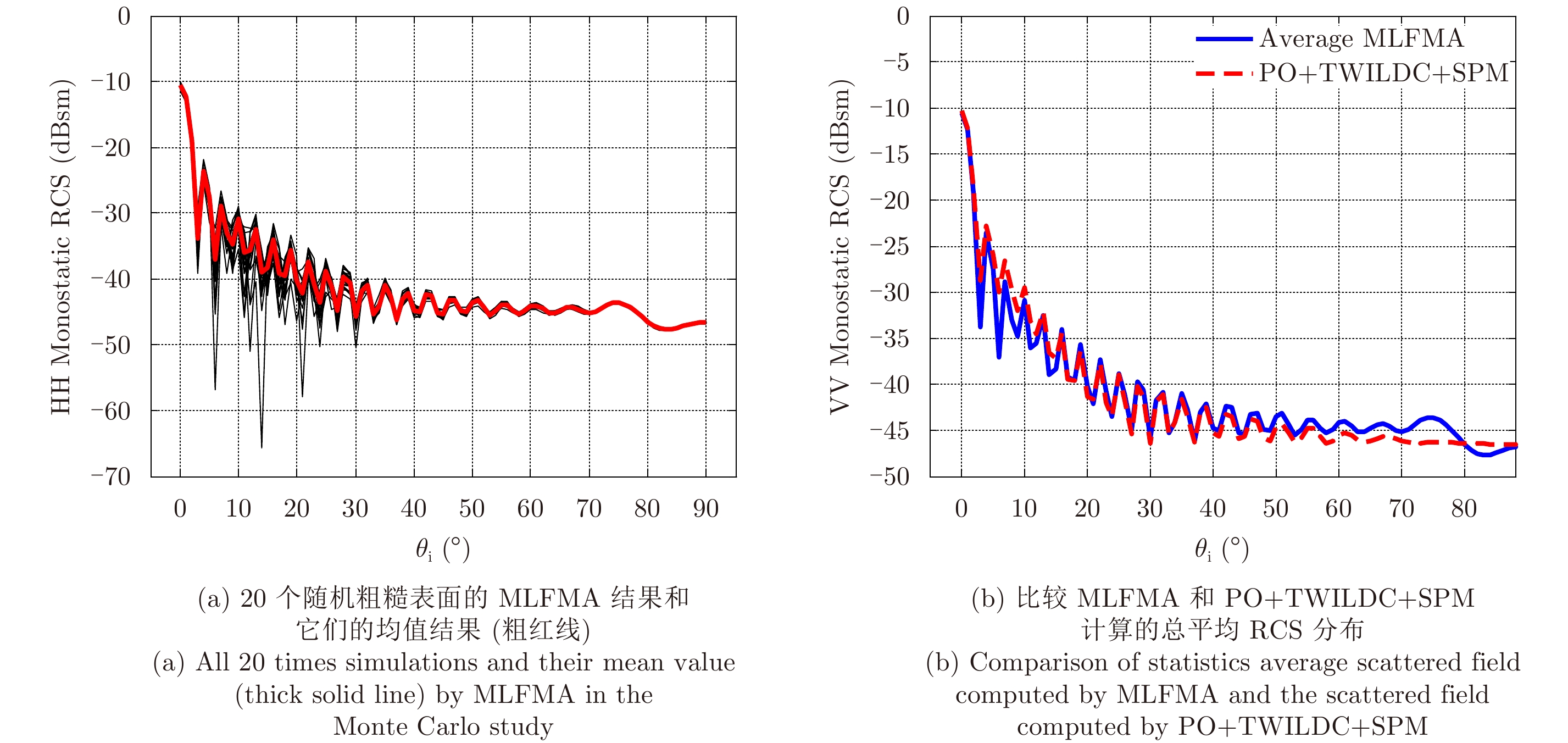
图10和图11分别利用MLFMA计算20次随机粗糙表面随入射俯仰角的单站VV和HH极化RCS值和均值和PO+TWILDC+SPM的计算结果,从中可以看出,在入射俯仰角从0°到50°范围内,两条曲线的峰值和变化趋势吻合很好。特别是在0°附近,也就是镜向附近吻合很好。当入射俯仰角大于50°时,两条曲线的变化趋势仍然是一致的。
|
图 10 单站VV极化RCS结果分布(300 GHz)。角度设置为
|
|
图 11 单站HH极化RCS结果分布(300 GHz)。角度设置为
|
本文研究了典型的无限薄金属平板在300 GHz的散射特性。利用MLFMA分别计算了在30 GHz和300 GHz无限薄微粗糙平板和相同尺寸的光滑平板的RCS,证实了在微波段可视为光滑金属目标,而在太赫兹波段可视为具有微粗糙起伏的目标。在太赫兹频段,一般目标电尺寸很大,提出采用PO+TWILDC+SPM高频混合算法计算太赫兹频段目标的RCS,并基于蒙特卡洛理论,利用MLFMA算法,比较VV和HH极化散射分布,验证了混合算法的有效性。当电尺寸越来越大时,MLFMA算法已受到严重限制,因此本文提出的高频混合算法是一个有效的太赫兹频段目标电磁散射特性预估手段。
| [1] |
许景周, 张希成. 太赫兹科学技术和应用[M]. 北京: 北京大学出版社, 2007.
Xu Jing-zhou and Zhang Xi-cheng. Terahertz Science Technology and Application[M]. Beijing, China: Peking University Press, 2007. (  0) 0)
|
| [2] |
王瑞君, 王宏强, 庄钊文, 等. 太赫兹雷达技术研究进展[J].
激光与光电子学进展, 2013, 50(4): 040001 Wang Rui-jun, Wang Hong-qiang, Zhuang Zhao-wen, et al.. Research progress of terahertz radar technology[J]. Laser & Optoelectronics Progress, 2013, 50(4): 040001 (  0) 0)
|
| [3] |
Cooper K B, Dengler R J, Llombart N, et al.. Penetrating 3-D imaging at 4-and 25-m range using a submillimeter-wave radar[J].
IEEE Transactions on Microwave Theory and Techniques, 2008, 56(12): 2771-2778. DOI:10.1109/TMTT.2008.2007081 ( 0) 0)
|
| [4] |
Li Z, Cui T J, Zhong X J, et al.. Electromagnetic scattering characteristics of PEC targets in the terahertz regime[J].
IEEE Antennas and Propagation Magazine, 2009, 51(1): 39-50. DOI:10.1109/MAP.2009.4939018 ( 0) 0)
|
| [5] |
Zhong X J, Cui T J, Li Z, et al.. Terahertz-wave scattering by perfectly electrical conducting objects[J].
Journal of Electromagnetic Waves and Applications, 2007, 21(15): 2331-2340. DOI:10.1163/156939307783134443 ( 0) 0)
|
| [6] |
Wu Z S. IR laser backscattering from an arbitrarily shaped dielectric object with rough surface[J].
Journal of Electronics (China), 1993, 10(4): 298-306. DOI:10.1007/BF02783158 ( 0) 0)
|
| [7] |
Ruck G T, Barrick D E, Stuart W D, et al.. Radar Cross Section Handbook[M]. New York: Plenum Press, 1970, Ch.9.
( 0) 0)
|
| [8] |
Ulaby F T, Moore R K, and Fung A K. Microwave Remote Sensing, vol. II[M]. Boston, USA: Artech House, 1978, Ch.12.
( 0) 0)
|
| [9] |
Johansen P M. Uniform physical theory of diffraction equivalent edge currents for truncated wedge strips[J].
IEEE Transactions on Antennas and Propagation, 1996, 44(7): 989-995. DOI:10.1109/8.504306 ( 0) 0)
|
| [10] |
Wu Z S and Cui S M. Bistatic scattering by arbitrarily shaped objects with rough surface at optical and infrared frequencies[J].
International Journal of Infrared and Millimeter Waves, 1992, 13(4): 537-549. DOI:10.1007/BF01010711 ( 0) 0)
|
| [11] |
Thorsos E I. The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum[J].
The Journal of the Acoustical Society of America, 1988, 83(1): 78-92. DOI:10.1121/1.396188 ( 0) 0)
|




