探地雷达(Ground Penetrating Radar, GPR),又称透地雷达,通过发射天线向地下发射宽带电磁波,接收天线接收散射回波进行地下未知区域的无损探测,主要应用于工程地质探测和安全防卫等场合[1,2]。宽带电磁波在地下传播的过程中,受到复杂多变的地下介质结构和外界随机噪声等多种因素的影响,会发生衰减、频散和多次散射干扰,这在很大程度上限制了探地雷达的探测分辨率和最终解释效果[3]。为了提高GPR回波的数据质量,提高探测效果,需要对GPR回波信号进行去噪处理,抑制GPR回波信号中的噪声和干扰。
针对不同的探测场景和后续数据处理需求,研究人员提出了多种GPR信号去噪算法,包括快速傅里叶变化法、小波变化法、独立分量分析(Independent Component Analysis, ICA)、经验模态分析(Empirical Mode Decomposition, EMD)、完全总体经验模态分解(Complete Ensemble Empirical Mode Decomposition, CEEMD)等[4–11],这些算法各有特点。段炜[8]提出对GPR信号使用小波变换特性对高频系数置零来去除噪声,实验验证了小波变换法比快速傅里叶变化法去噪效果好,但是也造成了高频细节丢失,同时该算法严重依赖于小波的形态。基于ICA理论, 张春成等[9]提出了一种针对步进频率GPR的ICA与中值滤波处理相结合的去噪算法,但是没有解决ICA的相位不确定性问题;陈玲娜[10]提出对GPR回波进行分频处理,通过选择固定频段的本征模态函数(Intrinsic Mode Function, IMF)进行重构从而抑制高频杂波和低频隐失波,再从原始信号中去掉高阶主成分分量进行去噪,但该算法需要人工剔除噪声后再重构信号,效率较低;Li等[11]提出了一种基于CEEMD的GPR信号处理方法,通过对GPR回波信号进行CEEMD分解,人工方式进行噪声辨识和去除,进而实现信号去噪。运用Hilbert-Huang变换,证明了该算法比经验模态分解和总体经验模态分解的谱分辨率更高,但是也需要通过人工判读的方式对各IMF进行判别,再进行信号重构。
针对上述算法中相位不确定的问题和CEEMD分解后需要人工判别信号分量的问题,本文提出一种基于自动反相校正和峰度值比较的GPR回波信号去噪方法。GPR含噪回波信号与随机噪声进行随机拟合,ICA分解,得到两路峰度值不等的信号,根据峰度值的高低分别判定为信号和噪声。信号分量进行自动反相校正,再进行CEEMD分解,得到多个IMF分量。将噪声分量的峰度值作为阈值,对信号分量分解后得到的多个IMF分量进行自动分类。高于该阈值的IMF分量视为信号分量,累加实现信号重构,完成去噪处理。分别用仿真数据和实测数据对所提的去噪算法进行了实验验证,结果显示,该方法在自动相位校正和自动分量判别方面大大提高了运算效率,提高了去噪效果。
2 基本原理 2.1 独立分量分析ICAICA是基于信号的高阶统计量,研究信号间的独立关系,将数据变换到相互独立的方向上,使经过ICA算法变换所得到的各个分量之间不仅正交,而且相互独立[12]。ICA处理的流程图如图1所示。

|
图 1 ICA流程图 Fig.1 The flow diagram of ICA |
在图1中,
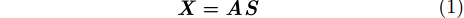
|
其中,
观测信号
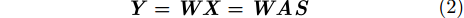
|
其中,
为了使信号
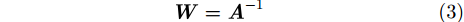
|
所以ICA就是求解一个最优的矩阵
CEEMD是一种基于EMD的通过噪声辅助的数据分析方法[13–17]。将固定比例的高斯白噪声添加到原始信号中,形成新的待分解信号,对新的待分解信号进行EMD分解得到IMF分量,用不同的白噪声分别进行
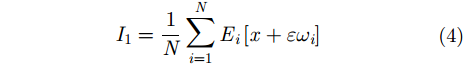
|
其中,
然后计算1阶残差
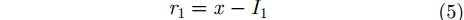
|
其中,
接着继续分解
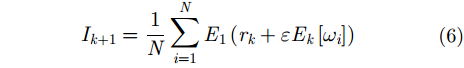
|
继续进行筛选,直到残差的极值个数不超过两个(残差为常量或单调函数)时停止,得到
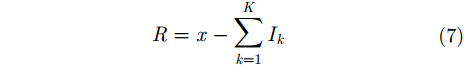
|
其中,
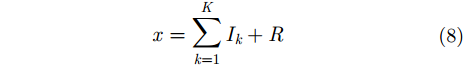
|
所以CEEMD是在EMD的基础上加入高斯白噪声再将分解成从高频到低频的分量,它比EMD分解效果更好,并且解决了模态混叠的问题。
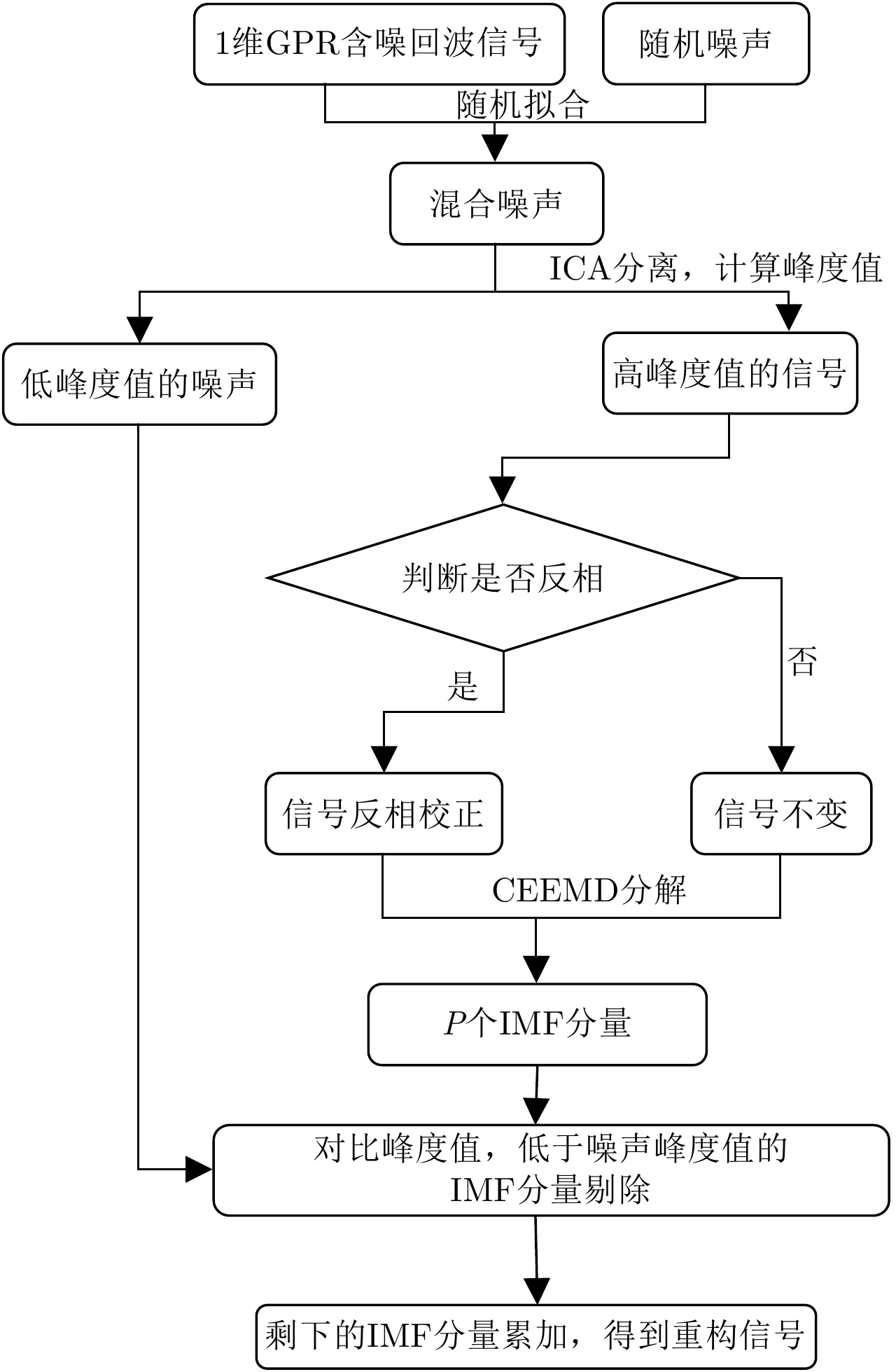
3 基于自动反相校正和峰度值比较的GPR去噪算法本文提出一种基于自动反相校正和峰度值比较的GPR信号去噪算法,流程图如图2所示。
|
图 2 算法流程图 Fig.2 The flow diagram of the algorithm |
具体来说,包括以下步骤:
步骤1 含噪GPR信号与随机噪声的拟合
设GPR获取的单道含噪数据为
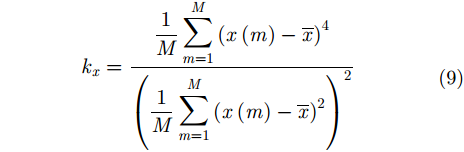
|
其中,
步骤2 ICA分离和自动校正
判断
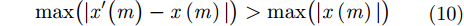
|
其中,
步骤3 CEEMD分解、自动阈值判别和重构恢复
对
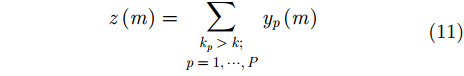
|
经过上述3个步骤,对原始含噪的GPR信号进行了去噪处理,压制了噪声分量,便于进行后续的成像等处理。
4 仿真与实测数据去噪实验下面分别运用仿真和实测数据对所提的GPR去噪算法进行验证。仿真数据采用gprMAX2.0[18]软件生成,实测数据为GPR对公路的探测数据。
4.1 仿真数据的处理首先设置仿真场景,使用gprMAX2.0软件生成不含噪的GPR信号,人为地加入噪声,将该含噪信号作为原始数据运用本文所提的去噪算法进行去噪处理。去噪后的信号再与gprMAX仿真生成的不含噪信号进行对比分析,验证本文所提算法的有效性。
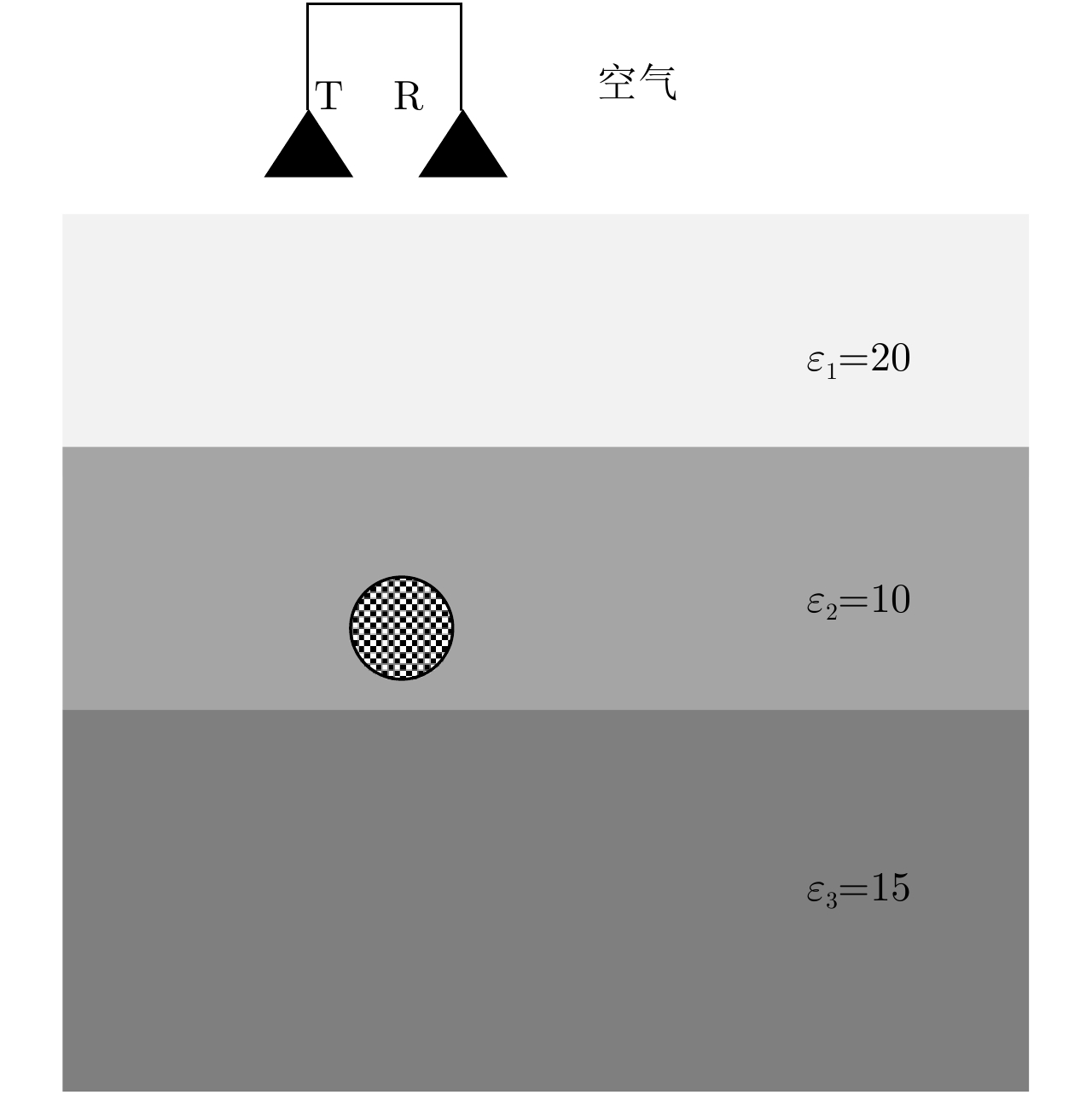
设定雷达探测场景如图3所示,地下介质有3层,第1、第2层的厚度均为15 cm,第1、第2、第3层的相对介电常数分别为20、10和15,一个半径为4 cm的金属管埋在第2层中,金属管的中心距第2层上表面6 cm,发射和接收天线位于金属管中心的正上方,距地表的高度为5 cm。发射信号为中心频率为900 MHz的Ricker子波,时窗取为40 ns,采样点数为6784,运行gprMAX得到GPR回波如图4所示。
|
图 3 GPR正演模型图 Fig.3 The forward model diagram of GPR |

|
图 4 正演模拟得到的GPR无噪回波信号图 Fig.4 The GPR no-noise echo signal by forward modeling |
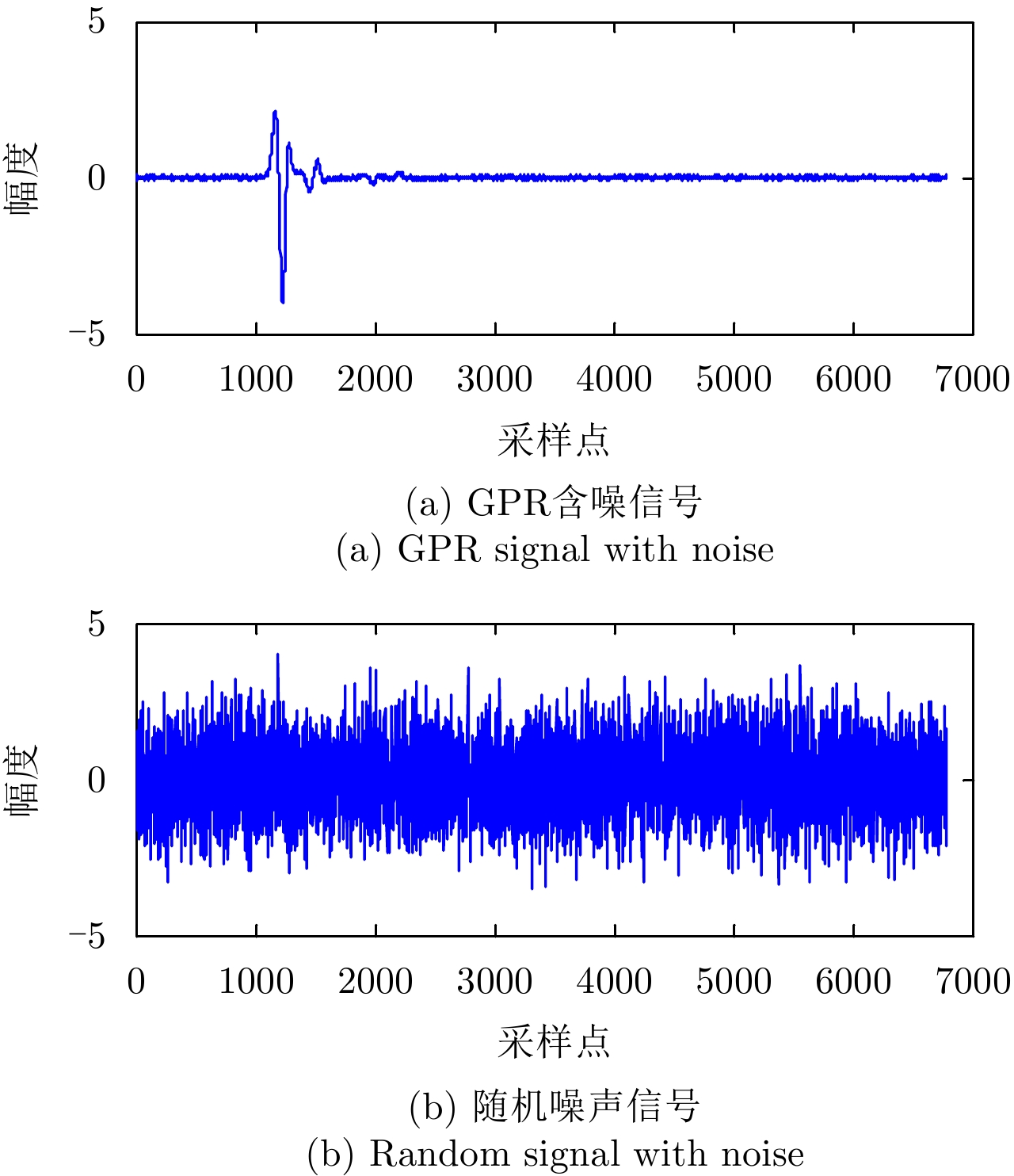
该信号为无噪的回波信号,为模拟生成含噪的GPR信号,人为地加入了随机白噪声,幅度为4.3328,方差为1.0513, SNR=19 dB,加入噪声后的GPR回波信号如图5(a)所示。按照所提的去噪算法,生成与含噪GPR信号长度相等的随机噪声,如图5(b)所示。
|
图 5 加入噪声后模拟得到的GPR含噪信号和产生的等长度的随机噪声信号 Fig.5 The GPR noise signal and the generated equal length random noise signal obtained by adding noise |
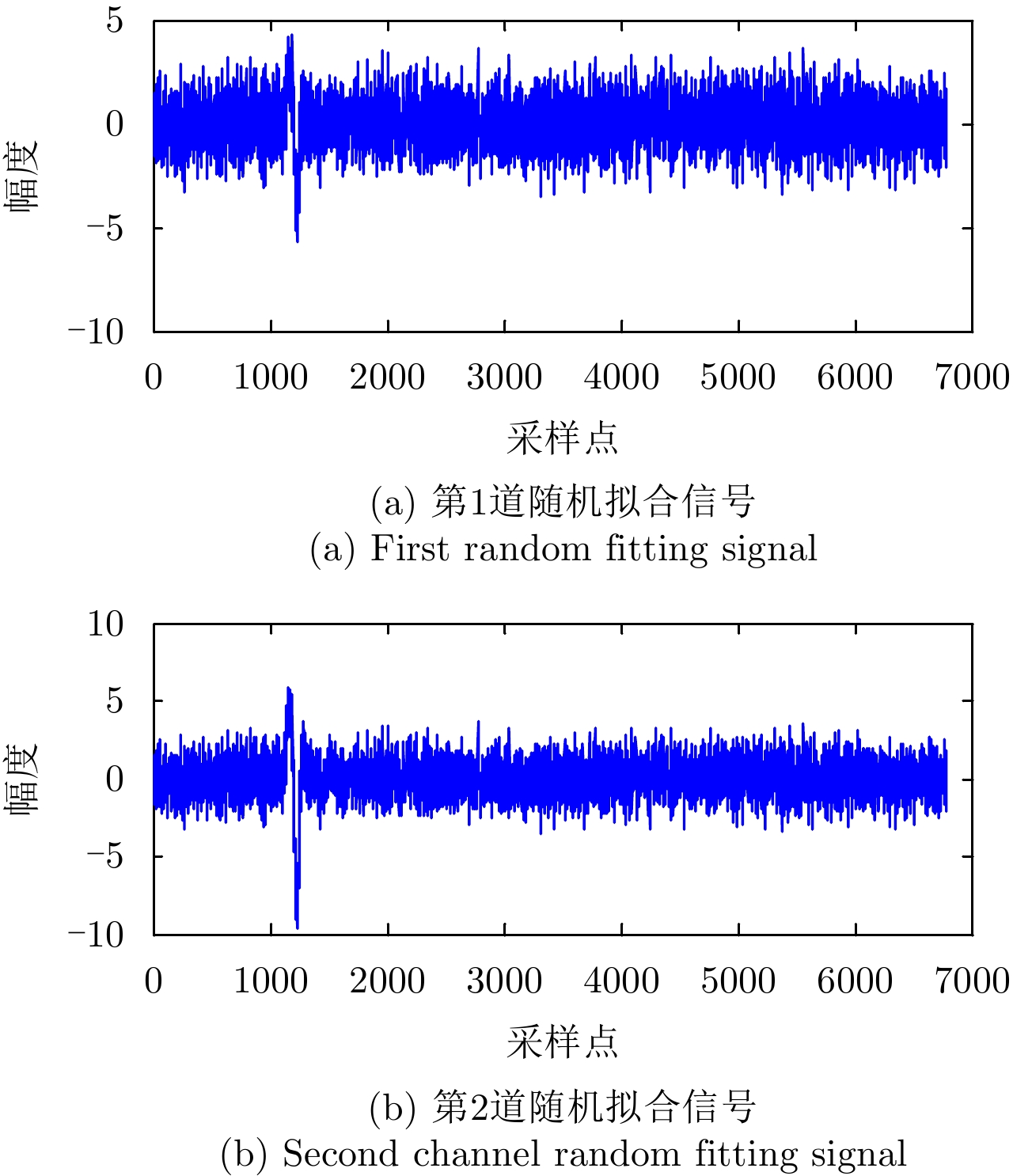
将图5(a)含噪GPR信号和图5(b)随机噪声进行随机拟合,即与一个2×2的矩阵
|
图 6 随机拟合后得到的两道信号 Fig.6 Two channel signals obtained after random fitting |

|
图 7 经过ICA算法后分离出的两道信号 Fig.7 Two channel signals separated by ICA algorithm |
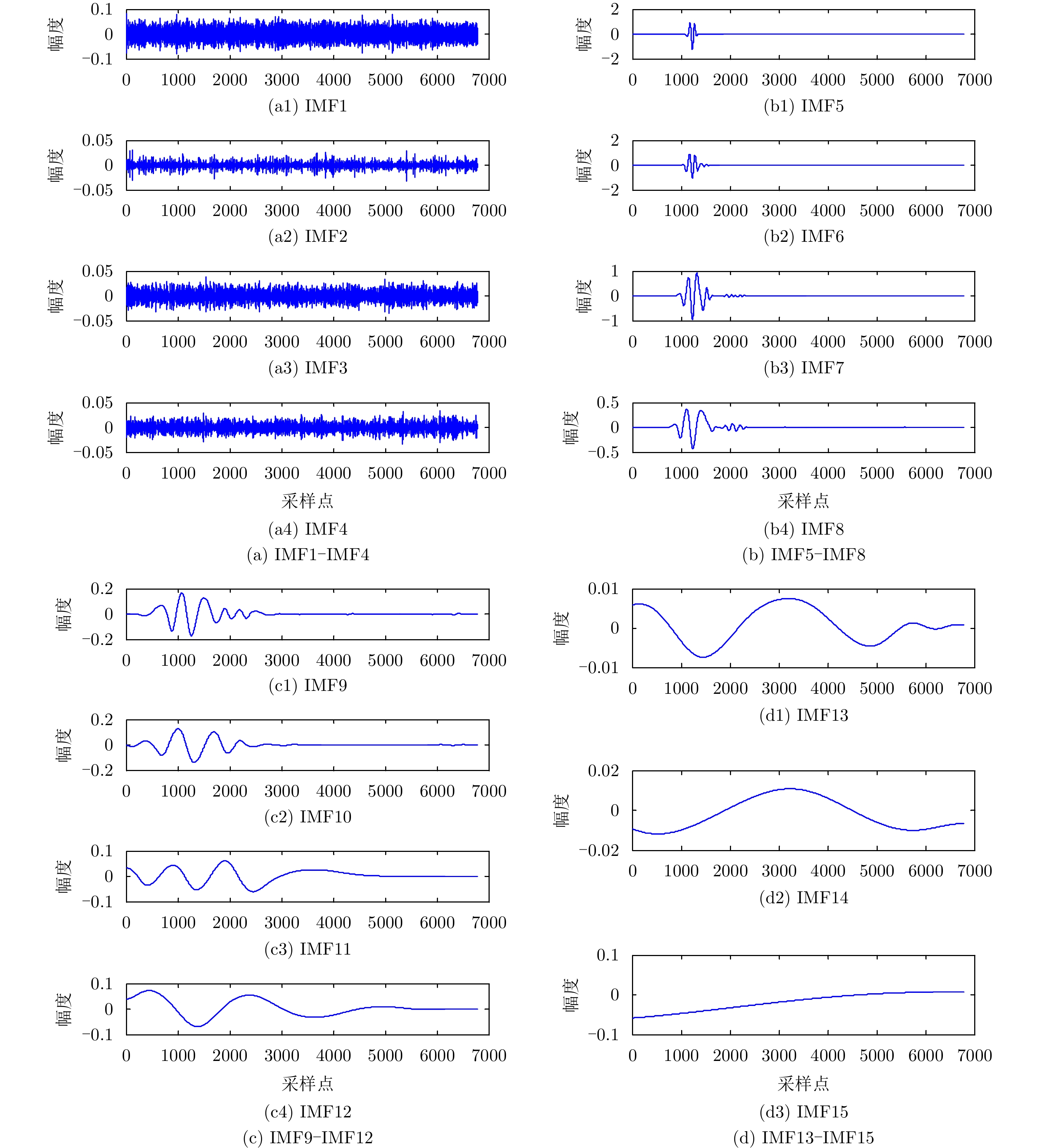
对图7(a)信号进行判断是否信号反相,该信号未反相,保持不变。再基于CEEMD算法的处理,得到图8所示的15个IMF分量。
|
图 8 经过CEEMD分解后的各IMF分量波形图 Fig.8 The IMF component waveform diagram after CEEMD decomposition |
对图8中的每一个IMF分量计算峰度值,峰度值分别为[2.1453, 2.1983, 2.7546, 2.8556, 75.0391, 41.8097, 25.3151, 16.4506, 9.3599, 7.3725, 3.2763, 3.7535, 3.9701, 1.6372, 1.7456]。计算ICA算法分离出来的图7(b)噪声信号的峰度值为2.9763。因此,将峰度值低于2.9763的IMF分量剔除,将剩余IMF分量进行累加得到的重构信号作为去噪后的信号,重构信号如图9所示。
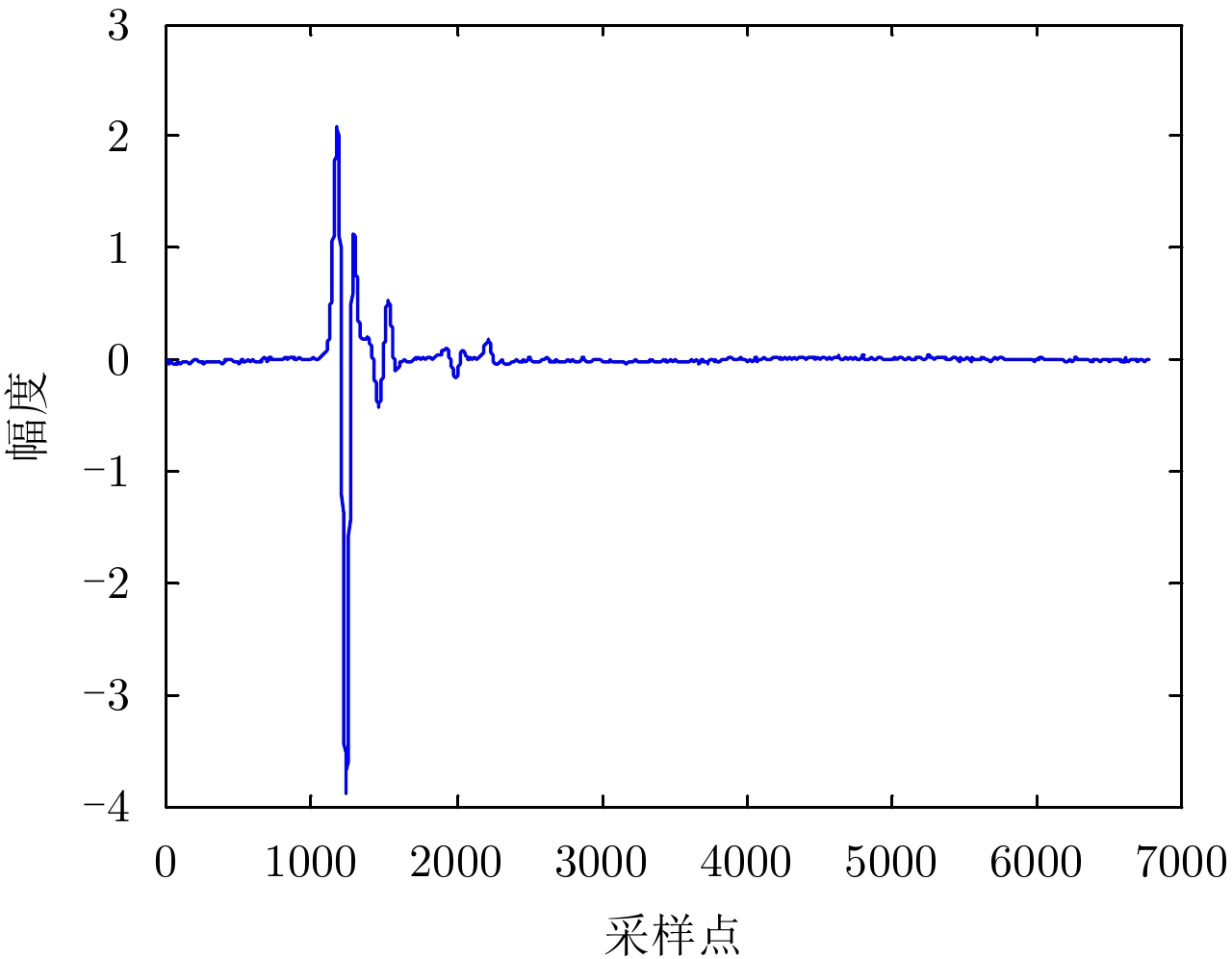
|
图 9 各IMF分量采用峰度值阈值分类后累加重构的信号 Fig.9 The signal of cumulative reconfiguration after the IMF components classified by kurtosis threshold value |
为衡量本文所提算法的效果,采用均方误差评价因子,计算方法如下:
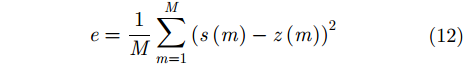
|
式中,
本仿真实验中,含噪的GPR回波的峰值为4.0418。运用本文提出的去噪算法得到去噪后的信号,用式(12)计算的去噪均方误差为0.0000283。
为定量对比分析本文所提的去噪算法与常规CEEMD去噪算法的性能,通过对原始gprMAX仿真得到的无噪回波信号加入不同幅度的噪声信号,生成不同SNR的含噪GPR回波信号,SNR的设置范围为[0, 20],点数为41点。每一SNR情况下,分别运用本文的去噪算法和常规CEEMD算法对该含噪GPR回波进行去噪处理,得到去噪回波,再与图4所示的无噪GPR回波进行对比分析,计算相对误差值。遍历整个SNR设置区间,得到各SNR情况下本文所提去噪算法和常规CEEMD去噪算法的误差曲线,如图10所示。
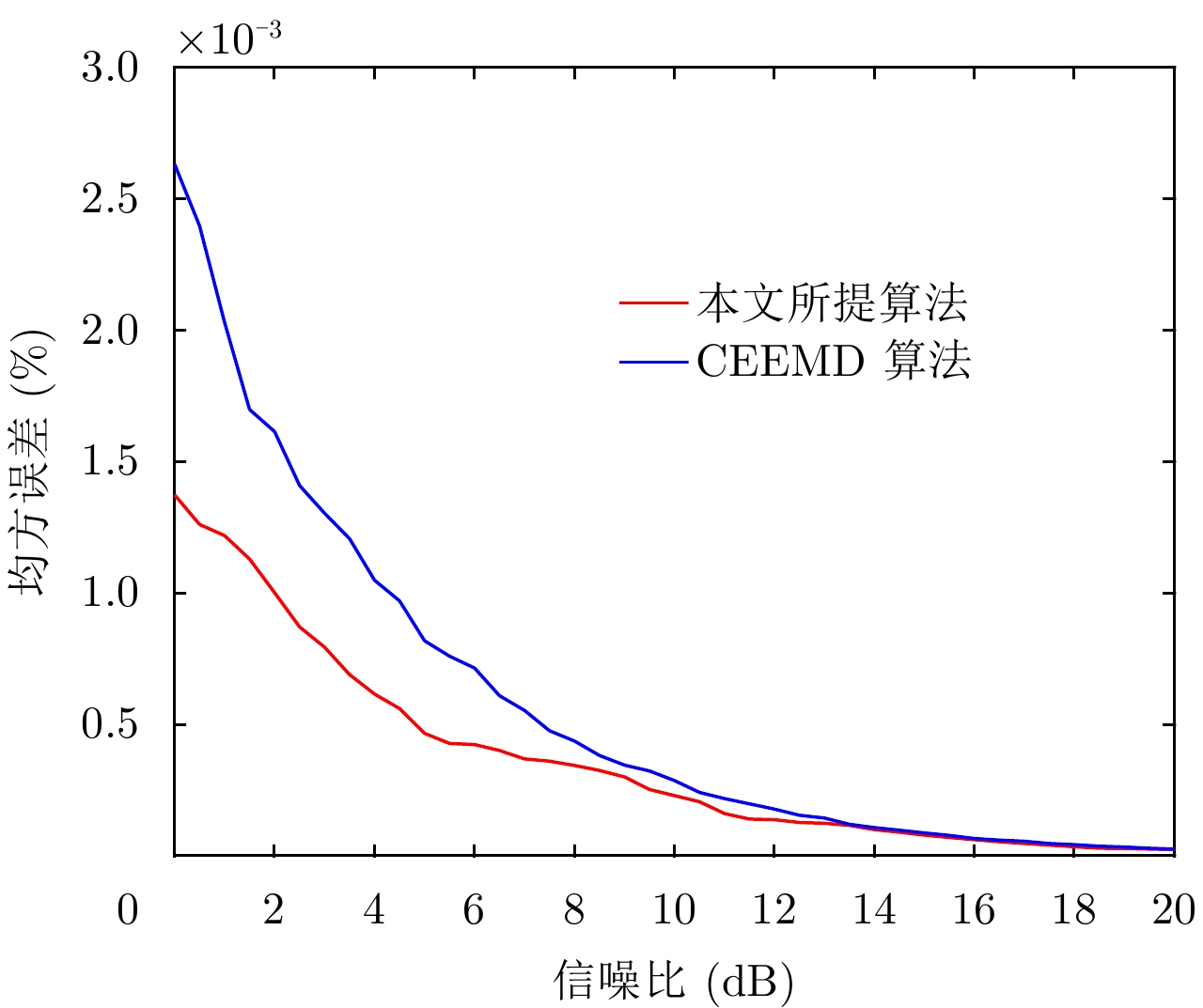
|
图 10 本算法和常规算法的去噪误差和信噪比的变化曲线对比图 Fig.10 The contrast diagram of the variation curve of denoising error and signa-to-noise ratio of the algorithm and the conventional algorithm |
从图10中可见,随着SNR的增大,所提的去噪算法和常规CEEMD去噪算法得到的结果的均方误差都随之降低。但在同一SNR情况下,本文去噪结果的相对误差更低,去噪性能高于常规CEEMD的去噪算法。
本文所提的算法,采用了自动相位校正和自动阈值判别,大大提高了计算效率。在CPU为Pentium® Dual-Core 2.00 GHz,内存为2.00 GB的PC上运行,上述单道GPR回波去噪处理耗时358.35 s。虽然对单道GPR回波去噪处理耗时需358.35 s,但常规的CEEMD算法在耗时266.55 s的基础上还需要进行人工判别IMF分量,相对而言,本算法无需每道数据处理过程中的人工判别,效率更高。
4.2 实测数据的处理采用中心频率为1 GHz的GPR对湖南省的邵怀高速进行沿线扫描探测,截取了其中一段数据,横向扫描长度为1.5 m,采样点数为187,纵向时窗为40 ns,采样点数为220。原始GPR B-Scan如图11所示。

|
图 11 原始GPR B-Scan图 Fig.11 The original GPR B-Scan |
运用本文所提的算法对该B-Scan剖面的187道数据进行逐道去噪处理,得到未去噪的B-Scan1和去噪后的原始B-Scan2剖面如图12所示。
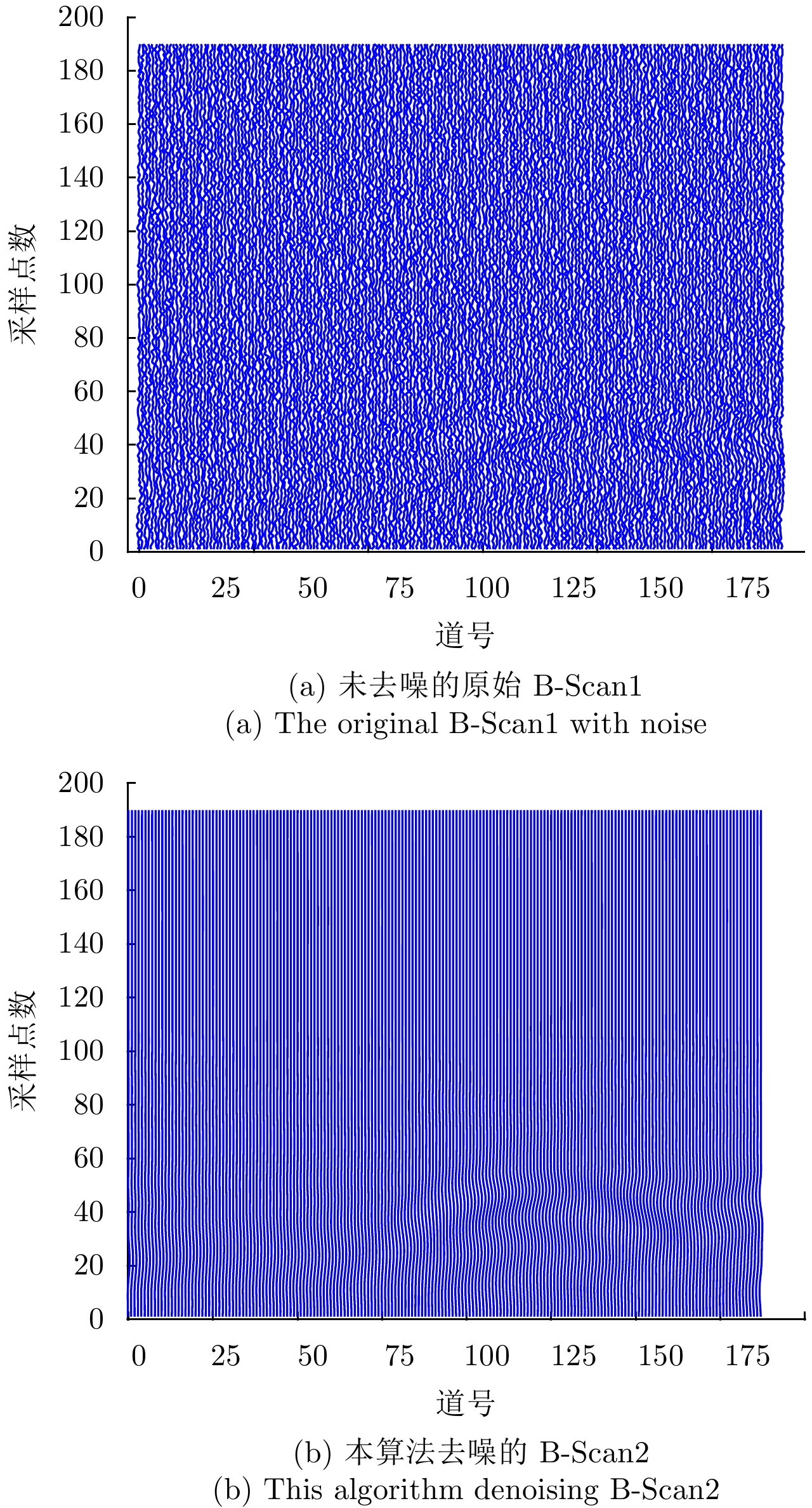
|
图 12 未去噪原始B-scan1和本算法去噪结果B-scan2对比图 Fig.12 The contrast diagram of the original B-Scan1 with noise and the denoising result of B-Scan2 in the present algorithm |
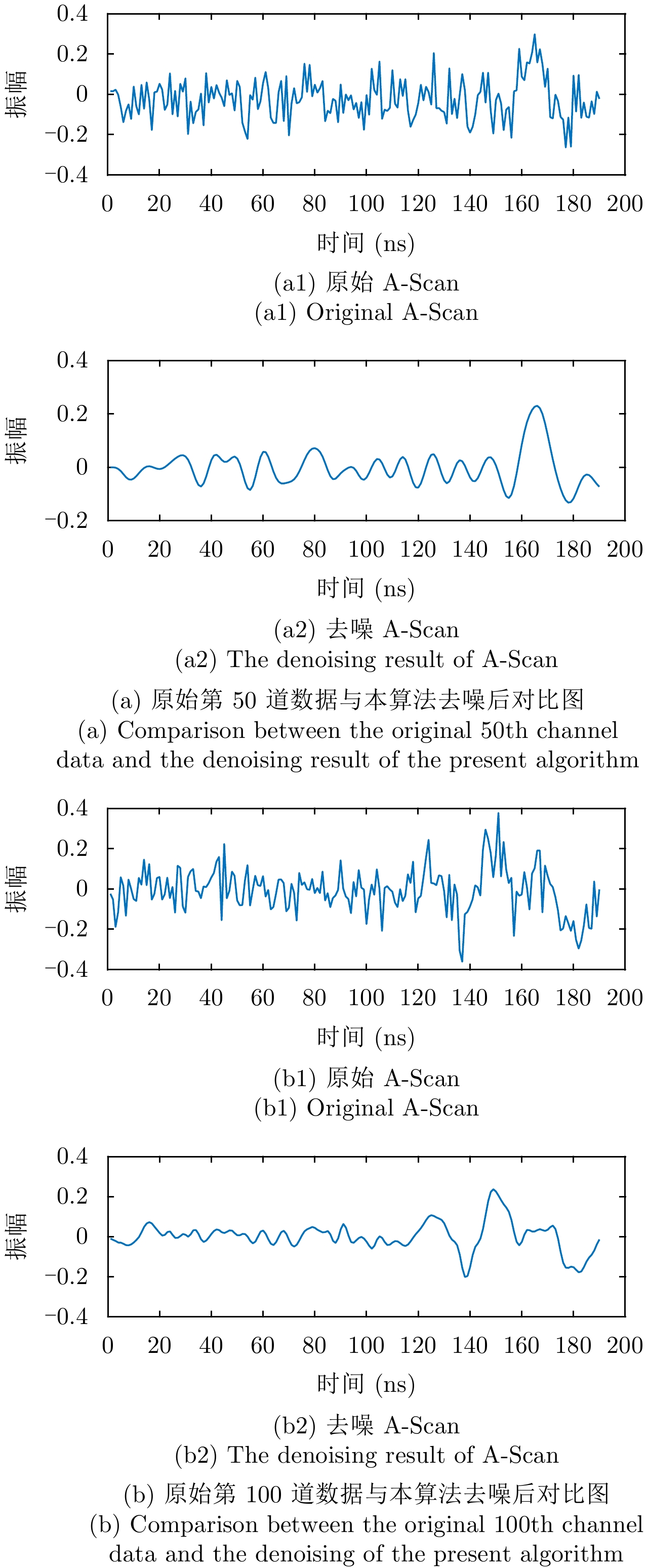
通过图12对比,可以看出本文算法在去噪效果方面的有效性。为了进一步体现其去噪效果,从去噪后中选取出第50和第100道数据与未进行去噪的原始数据进行对比,如图13所示。
|
图 13 未去噪原始A-Scan和本算法去噪结果A-Scan对比图 Fig.13 The contrast diagram of the original A-Scan with noise and the denoising result of A-Scan in the present algorithm |
通过图13中第50和第100道数据与未进行去噪的原始数据进行对比,从对比结果来看,本算法的去噪效果不错,再一次验证了本文算法去噪效果方面的有效性。
5 总结GPR回波信号的去噪处理决定着后续的数据解译质量。针对现有去噪算法的相位不确定和人工判别IMF分量的问题,本文提出基于自动反相校正和峰度值比较的去噪算法,设计了相位判别因子,实现了ICA分解后的信号相位自动判别和校正,设计了基于峰度值比较的IMF分量自动筛选,阈值选择为ICA算法分离出来的噪声信号的峰度值。该算法避免了ICA分解后的相位不定性,且在CEEMD分解后无需传统的人工方式进行各IMF分量的筛选。通过对仿真和实测数据的处理,验证了本文所提算法的有效性。后续研究工作将集中在CEEMD算法运算效率的优化上,进一步提高去噪效率。
| [1] |
Harry M J, 雷文太, 童孝忠, 周旸, 等译. 探地雷达理论与应用[M]. 北京: 电子工业出版社, 2011: 2–24.
Harry M J. Lei Wen-tai, Tong Xiao-zhong, Zhou Yang, et al.. Ground Penetrating Radar: Theory and Application[M]. Beijing: Publishing House Of Electronics Industry, 2011: 2–24. (  0) 0)
|
| [2] |
冯晅, 曾昭发, 刘四新, 等. 探地雷达信号处理[M]. 北京: 科学出版社, 2014: 3–15.
Feng Xuan, Zeng Zhao-fa, Liu Si-xin, et al.. Ground Penetrating Radar Signal Processing[M]. Beijing: Science Press, 2014: 3–15. (  0) 0)
|
| [3] |
杨峰, 彭苏萍. 地质雷达探测原理与方法研究[M]. 北京: 科学出版社, 2010: 5–30.
Yang Feng and Peng Su-ping. Study on the Principle and Method of GPR Detection[M]. Beijing: Science Press, 2010: 5–30. (  0) 0)
|
| [4] |
石国杰, 王晋国, 侯兆阳, 等. 地质雷达数据处理新方法研究[J].
洛阳理工学院学报(自然科学版), 2017, 27(1): 42-44. Shi Guo-jie, Wang Jin-guo, Hou Zhao-yang, et al. Study on new methods of ground penetrating radar data analysis[J]. Journal of Luoyang Institute of Science and Technology (Natural Science Edition), 2017, 27(1): 42-44. DOI:10.3969/i.issn.1674-5403.2017.01.012 (  0) 0)
|
| [5] |
王超, 沈斐敏. 小波变换在探地雷达弱信号去噪中的研究[J].
物探与化探, 2015, 39(2): 421-424. Wang Chao and Shen Fei-min. Study of wavelet transform in ground penetration radar weak signal denoising[J]. Geophysical and Geochemical Exploration, 2015, 39(2): 421-424. DOI:10.11720/wtyht.2015.2.35 (  0) 0)
|
| [6] |
许军才, 刘立桥, 任青文, 等. 探地雷达信号的EEMD时域分析方法[J].
合肥工业大学学报(自然科学版), 2015, 38(5): 639-642. Xu Jun-cai, Liu Li-qiao, Ren Qing-wen, et al. EEMD analysis of GPR signal in time domain[J]. Journal of Hefei University of Technology (Natural Science Edition), 2015, 38(5): 639-642. DOI:10.3969/j.issn.1003-5060.2015.05.014 (  0) 0)
|
| [7] |
Abujarad F and Omar A. Comparison of Independent Component Analysis (ICA) algorithms for GPR detection of non-metallic land mines[C]. Proceedings of SPIE Image and Signal Processing for Remote Sensing XII, Stockholm, Sweden, 2006: 1–12.
( 0) 0)
|
| [8] |
段炜. 基于小波变换的探地雷达信号去噪方法研究[D]. [硕士论文], 中南大学, 2008.
Duan Wei. Research on denoising method of ground penetrating radar signal based on wavelet transform[D]. [Master dissertation], Central South University, 2008. (  0) 0)
|
| [9] |
张春城, 周正欧. 基于ICA的步进频率探地雷达目标信息提取研究[J].
安徽理工大学学报(自然科学版), 2009, 29(2): 1-4. Zhang Chun-cheng and Zhou Zheng-ou. Research on target information extraction in step frequency ground penetrating radar data based on independent component analysis[J]. Journal of Anhui University of Science and Technology (Natural Science), 2009, 29(2): 1-4. DOI:10.3969/j.issn.1672-1098.2009.02.001 (  0) 0)
|
| [10] |
陈玲娜. 基于CEEMD和PCA的探地雷达数据处理研究与应用[D]. [硕士论文], 吉林大学, 2016.
Chen Ling-na. The study and application of GPR data processing based on CEEMD and PCA[D]. [Master dissertation], Jilin University, 2016. (  0) 0)
|
| [11] |
Li J, Liu C, Zeng Z F, et al. GPR signal denoising and target extraction with the CEEMD method[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(8): 1615-1619. DOI:10.1109/LGRS.2015.2415736 ( 0) 0)
|
| [12] |
明锋, 杨元喜, 曾安敏. 共模误差PCA与ICA提取方法的比较[J].
大地测量与地球动力学, 2017, 37(4): 385-389. Ming Feng, Yang Yuan-xi, and Zeng An-min. Analysis and comparison of common mode error extraction using principal component analysis and independent component analysis[J]. Journal of Geodesy and Geodynamics, 2017, 37(4): 385-389. DOI:10.14075/j.jgg.2017.04.012 (  0) 0)
|
| [13] |
Wu Z H and Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J].
Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 ( 0) 0)
|
| [14] |
Yen J R, Shieh J S, and Huang N E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method[J].
Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. DOI:10.1142/S1793536910000422 ( 0) 0)
|
| [15] |
Torres M E, Colominas M A, Schlotthauer G, et al.. A complete ensemble empirical mode decomposition with adaptive noise[C]. Proceedings of 2011 IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 2011: 4144–4147. DOI: 10.1109/ICASSP.2011.5947265.
( 0) 0)
|
| [16] |
王姣, 李振春, 王德营. 基于CEEMD的地震数据小波阈值去噪方法研究[J].
石油物探, 2014, 53(2): 164-172. Wang Jiao, Li Zhen-chun, and Wang De-ying. A method for wavelet threshold denoising of seismic data based on CEEMD[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 164-172. DOI:10.3969/j.issn.1000-1441.2014.02.006 (  0) 0)
|
| [17] |
Colominas M A, Schlotthauer G, and Torres M E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing[J].
Biomedical Signal Processing and Control, 2014, 14: 19-29. DOI:10.1016/j.bspc.2014.06.009 ( 0) 0)
|
| [18] |
Warren C, Giannopoulos A, and Giannakis I. gprMax: Open source software to simulate electromagnetic wave propagation for ground penetrating radar[J].
Computer Physics Communications, 2016, 209: 163-167. DOI:10.1016/j.cpc.2016.08.020 ( 0) 0)
|




