多基站雷达无源定位系统中,雷达本身不发射电磁波,而是借助外辐射源信号或直接截获目标辐射源发射信号进行处理以实现相应的功能;多基站雷达无源定位具有功耗低、隐蔽性好等优势,在军事、民事中得到广泛应用[1–7]。常见的多基站雷达无源定位算法有间接定位算法和直接定位(Direct Position Determination, DPD)算法,也称为两步定位算法和一步定位算法。前者首先从截获的目标观测信号中提取相关参数(如到达角(Angle Of Arrival, AOA)、到达时差(Time Difference Of Arrival, TDOA)等),然后利用提取到的参数通过数学运算获得目标位置[1–4]。后者则没有参数提取的过程,而是将截获的信号进行简单处理后直接传输至中央处理器并对目标进行定位[5–7]。两步定位算法中,参数提取的过程在每个接收雷达基站独立进行,忽略了所有观测回波信号对应同一个目标这一客观约束,在低信噪比(Signal-to-Noise Ratio, SNR)情况下其定位性能将严重恶化;而DPD算法则能充分利用各接收基站的观测回波信息,具有比两步定位算法更优的定位性能[5]。
针对多基站雷达无源直接定位这一背景,Weiss推导了在发射信号已知和发射信号未知两种情况下的最小二乘估计表达式[5]。该DPD算法只需通过对目标所在2维平面或3维空间区域进行网格搜索,寻找使相应的目标函数最大化的网格点作为辐射源目标的位置估计。对于发射信号已知的情况(例如训练信号或同步信号),通过直接搜索待估参数使得目标函数最大化即可实现目标的定位;对于更为常见的发射信号未知的情况,根据观测信号构建与目标位置相关的矩阵,并通过一定的数学变换直接搜索该矩阵的最大特征值进而完成参数的估计。一般情况下,前者(DPD-known算法)可以获得最佳的定位性能,而后者(DPD-unknown算法)由于有部分发射信号特征信息的丢失,其定位性能要劣于前者。在很多情况下,辐射源发射信号的模型已知而具体参数未知,例如未知信号参数的线性调频(Linear Frequency Modulation, LFM)信号,可通过估计发射信号参数来进一步提高目标定位精度。
LFM信号具有低截获率、高分辨率、大时宽带宽积等优势,广泛应用于雷达、通信及地震识别等领域[8,9]。因此,对于LFM信号辐射源进行多基站雷达无源直接定位具有重要的理论意义和应用价值。文献[6]为解决单个LFM信号辐射源的定位问题,通过短时傅里叶变换(Short Time Fourier Transform, STFT)推导了联合估计LFM信号参数和目标位置的DPD算法,其定位精度明显优于DPD-unknown算法。但是上述DPD算法无法实现多目标定位,因此在实际场景中对多个LFM信号辐射源的定位问题亟待解决。
为确定监测区域内多个未知信号参数的LFM信号辐射源的位置,本文提出一种基于分数傅里叶变换(FRactional Fourier Transform, FRFT)和DPD算法相结合的多目标定位算法。FRFT作为一种广义的傅里叶变换(Fourier Transform, FT),在波传播和光学领域是研究、分析和处理信号的一种重要手段[9–12]。因FRFT对LFM信号具有良好能量聚集性,被普遍用来估计LFM信号的相关参数[11,13]。本文首先对观测信号应用FRFT得到其功率谱,并结合目标提取算法进而实现辐射源数量估计;其次利用基本分类方法对估计得到的相关信号参数进行分类,并对感兴趣参数空间进行多次4维网格搜索进而实现多辐射源位置及相应信号参数估计;最后,通过仿真实验验证本文提出算法的定位性能。仿真结果表明该算法能够准确定位监测区域内的多个辐射源目标,且定位精度优于DPD-unknown算法。
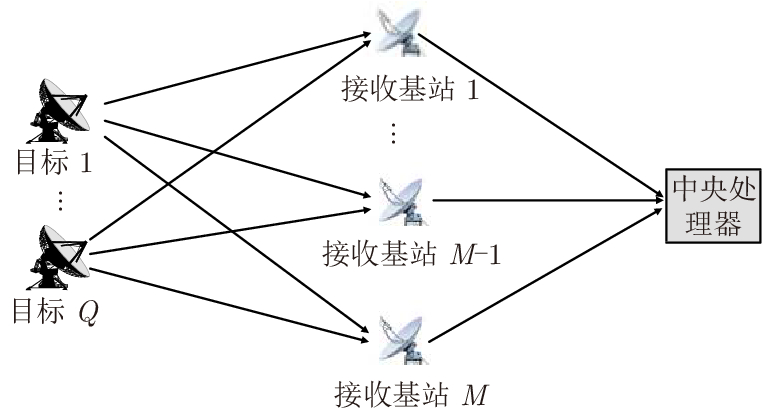
2 信号模型与问题导出如图1所示,在2维笛卡尔坐标系下,
|
图 1 2维定位场景示意图 Fig.1 Two-dimensional scenario for location determination |
假设从目标
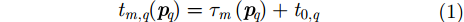
|
其中,
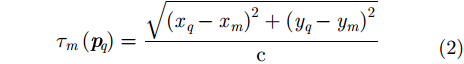
|
c为光速。
假设所有基站均能接收到目标信号,则在第
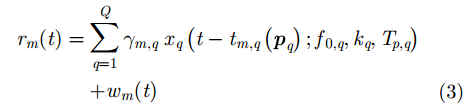
|
其中,

|
其中,
为了方便描述,可将式(3)中的接收信号表示为:

|
其中
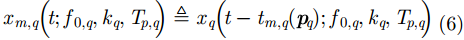
|
经采样后,式(5)可表达为如下向量形式:
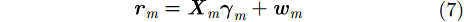
|
其中
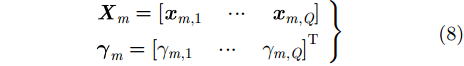
|
且
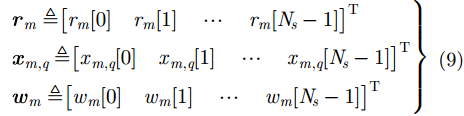
|
其中,
由以上分析可知,未知待估参数包括所有目标的衰减系数
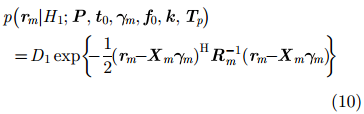
|
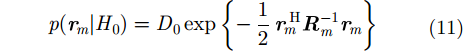
|
其中,

|
由于
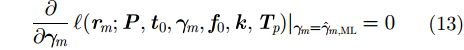
|
则
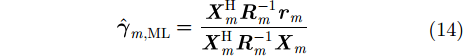
|
将其代回式(12),可得如下对数似然比函数:
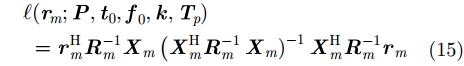
|
式(15)中全部的未知参数可以通过对参数空间进行穷尽搜索得到[14],即
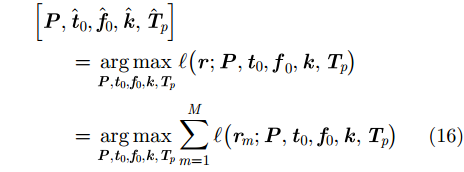
|
式(16)即是对辐射源位置
本文提出的基于FRFT的多目标直接定位算法(DPD-FRFT算法)思路:首先,利用FRFT处理接收信号得到其功率谱,并应用目标提取算法提取功率谱局部极值点,进而获得目标数量的估计值;然后,基于FRFT域中相应参数与LFM信号参数的关系式,可以得到相关信号参数的估计值;其次,利用基本分类算法可进一步将多目标问题转化为多个单目标问题;最后,基于4维网格搜索方法便可获得单个目标的位置及相应信号参数估计值。高维似然估计算法是理论最优的,而DPD-FRFT算法作为一种次优的定位算法,通过将高维的多目标定位问题转化为多个低维的单目标定位问题来降低计算量,因此可以认为该算法是在计算复杂度和定位精度之间折中的定位算法。
3.1 分数傅里叶变换简介常见的FRFT定义为[13]:
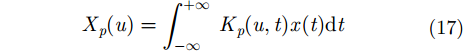
|
其中,
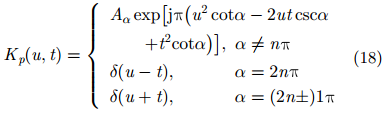
|
其中,

|
假设
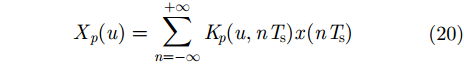
|
由于FRFT是传统FT的广义形式,具有与FT类似的线性性质,即
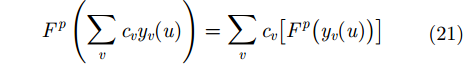
|
其中,
因时间量纲(s)和频率量纲(Hz)不一致,且尺度也不统一,FRFT作为一种时频变换工具,在该种情况下不便于其进行离散化处理。为了计算简便,Ozaktas提出采样性算法[8]。该算法首先引入量纲归一化因子
利用FRFT可以把LFM信号重构到新的LFM基函数空间当中。该空间由调频斜率可改变的LFM信号构成,且具有与利用FT研究单频信号时会在相应频率处表现出冲激函数特性完全相同的性质[13]。仅当其旋转角度
考虑一个离散LFM信号,其调频斜率为

|
由式(17)、式(18)可知,对式(22)作FRFT可得:
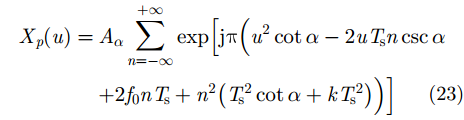
|
此即式(22)的功率谱函数。当
由于FRFT具有线性叠加性,因此对于多辐射源发射的多个LFM信号只需进行信号叠加,根据能量聚集后局部极值点的数量,利用图像膨胀算法[16]便可确定目标数量的估计值。由于高斯白噪声不具有冲激特性,因此该方法不受噪声影响。
3.3 信号参数分类参见文献[13],假设式(23)满足能量聚集特性,此时尖峰脉冲所对应的

|
其中,S是
对估计得到的调频斜率
由式(24)可知,任意LFM信号的调频斜率
对于目标
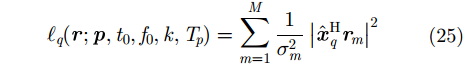
|
其中,
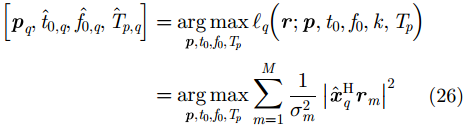
|
同式(16)相比,式(26)只需对参数空间展开4维搜索,在一定程度上降低了算法的计算复杂度。
综上,本文提出的定位算法流程图如图2所示。
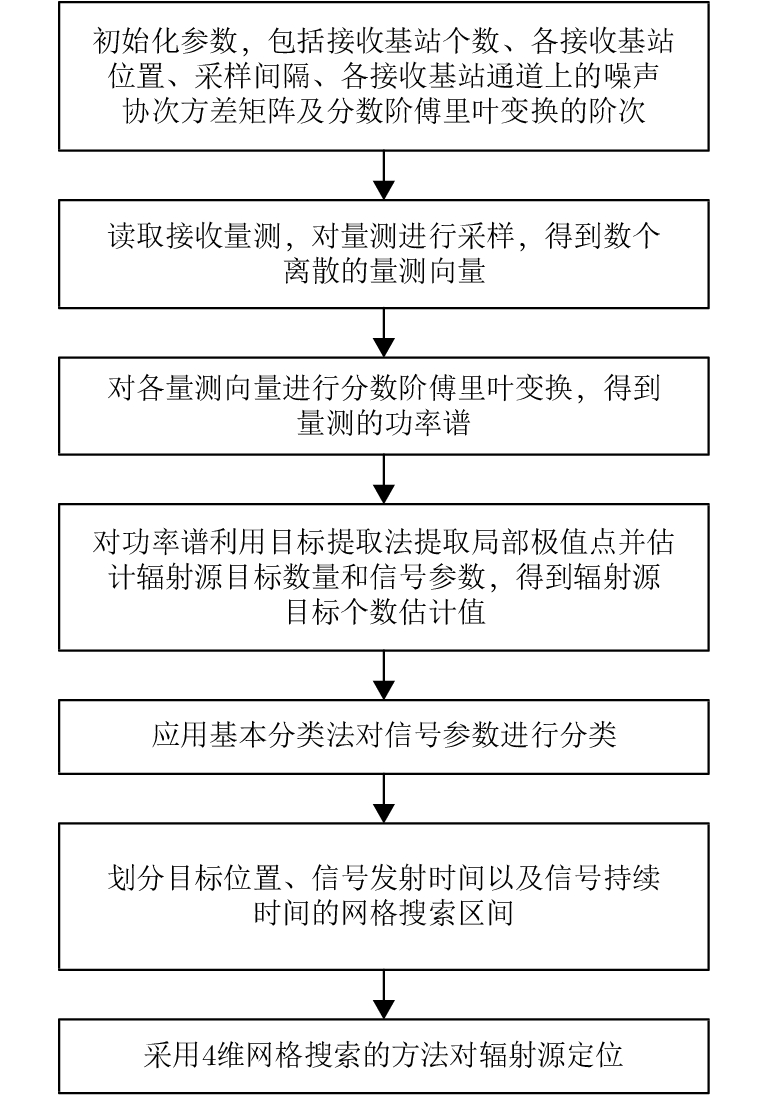
|
图 2 定位算法流程图 Fig.2 Flow chart for location determination algorithm |
本节通过Monte Carlo仿真实验对比分析本文提出的DPD-FRFT算法、文献[5]中提出的DPD-unknown算法与DPD-known算法的性能。显然,前文推导的高维最大似然估计器在理论上是最优的,相比DPD-FRFT算法、DPD-unknown算法与DPD-known算法有最小的估计误差。然而由于计算的限制,实施该高维最大似然估计器花费的时间过长、代价过大,因此用DPD-known算法替代该算法。可以认为,DPD-known算法由于利用了发射信号完整的无误差的信息,因此是这几种定位算法误差的下界。
如图3所示,在一个2维笛卡尔坐标平面上,3个辐射源的位置坐标为
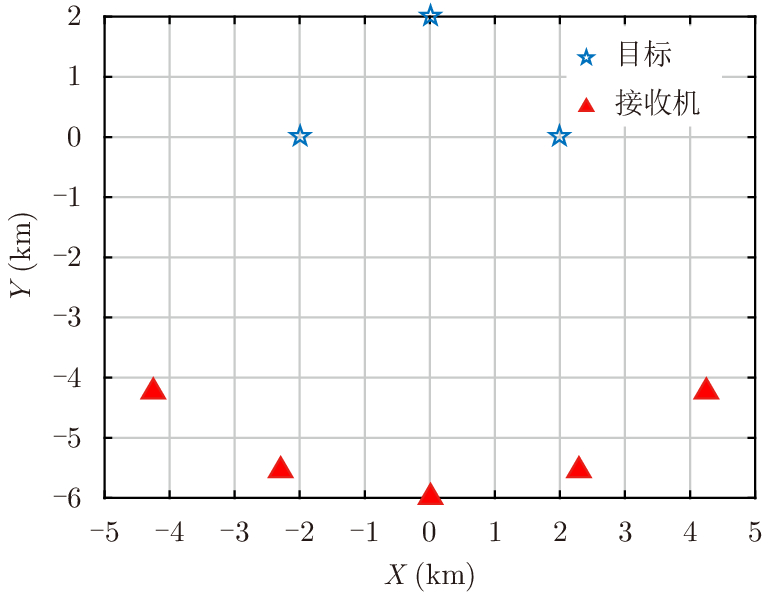
|
图 3 仿真场景示意图 Fig.3 Simulation scenario |
辐射源均发射LFM信号,其信号参数如表1所示。
| 表 1 信号参数设置 Tab.1 Signal parameter setting |
观测信号与式(5)具有相同形式,该信号由3个经过一定时延的LFM信号和噪声叠加得到。对该信号进行FRFT,得到的3维功率谱如图4所示。
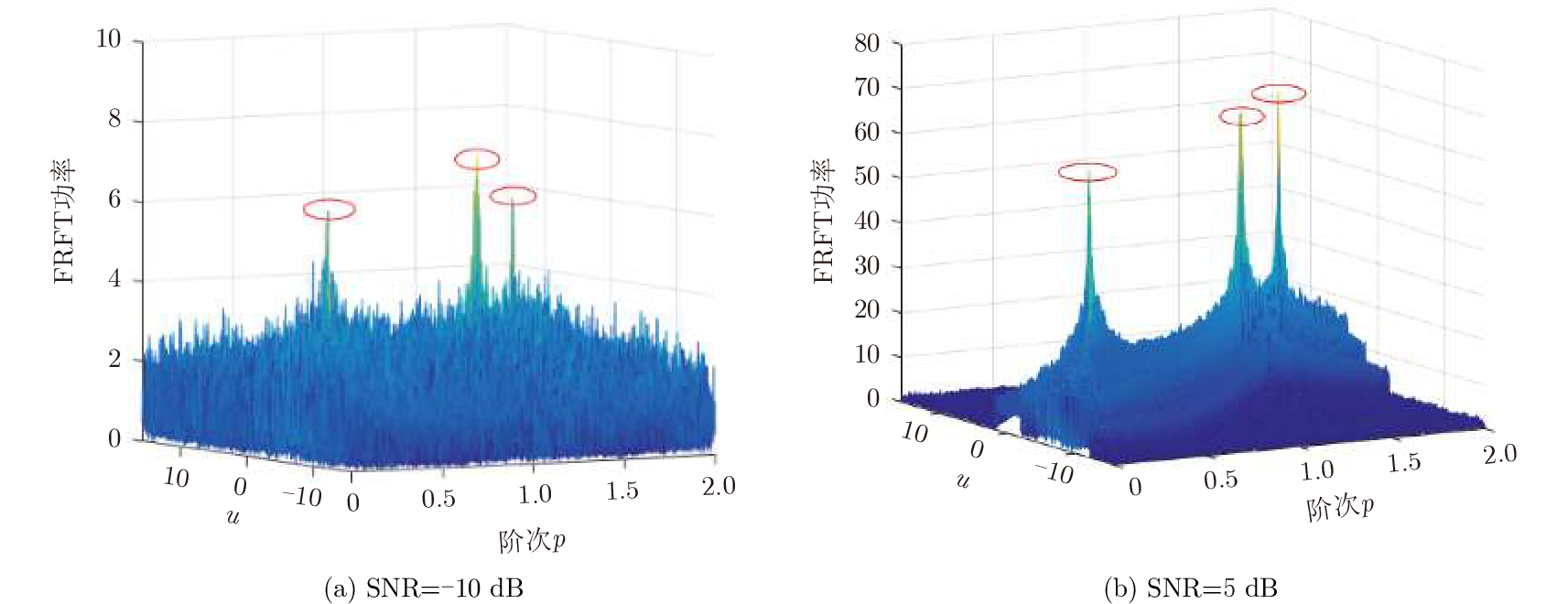
|
图 4 接收信号的FRFT功率谱3维分布图 Fig.4 Three-dimensional FRFT power spectrum for received signal |
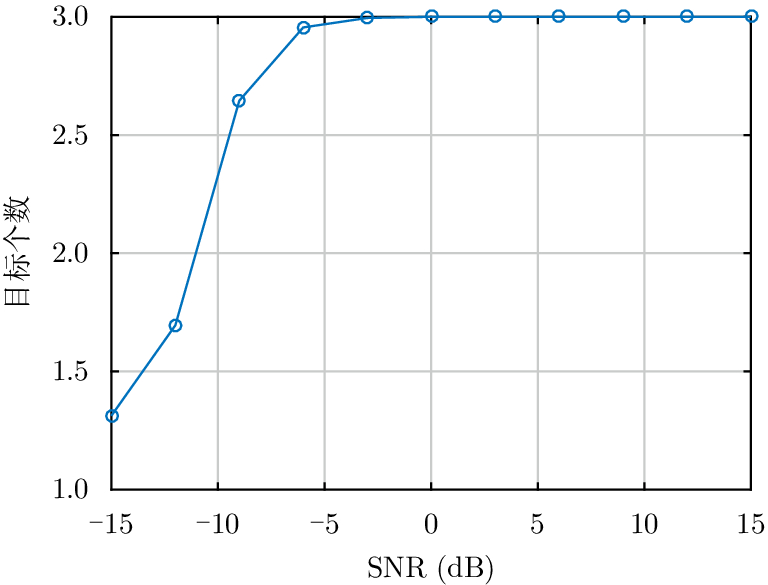
由图4可知,当SNR=5 dB时,观测信号的功率谱中明显有3个局部极值点(红色椭圆标出);但当SNR=–10 dB时,虽然也可分辨出功率谱的3个极值点,但由于受噪声影响并不明显。这表明应用FRFT可有效实现对LFM信号辐射源数量的估计,但受信噪比影响严重。其具体关系如图5所示。
由图5可知,在SNR大于0 dB左右时目标数量能够得到较好的估计。
|
图 5 目标数量估计与SNR关系 Fig.5 Relation between source number and SNR |
本文用均方根误差(Root Mean Square Error, RMSE)衡量定位精度,其定义如下:

|
其中,
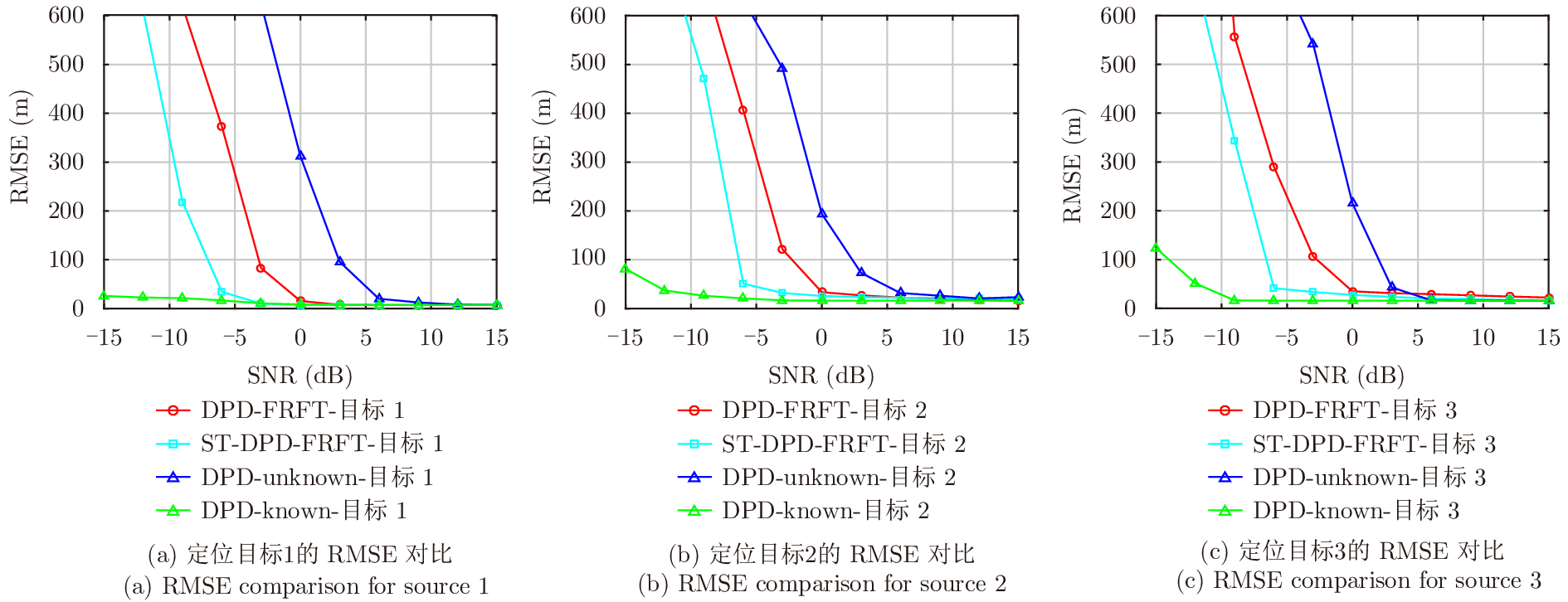
仅考虑单目标情况下DPD-unknown算法、DPD-known算法和本文提出的ST-DPD-FRFT算法(针对单个目标的DPD-FRFT算法)的性能比较。需要注意的是,该种对比方式使得DPD-unknown算法有一定的优势;但若ST-DPD-FRFT算法的定位性能优于DPD-unknown算法,那么该算法同多目标DPD算法将具有更大的优势。
由图6可知,在高信噪比下(约为
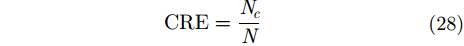
|
其中,
|
图 6 4种算法定位误差对比 Fig.6 RMSE comparison for four algorithms |
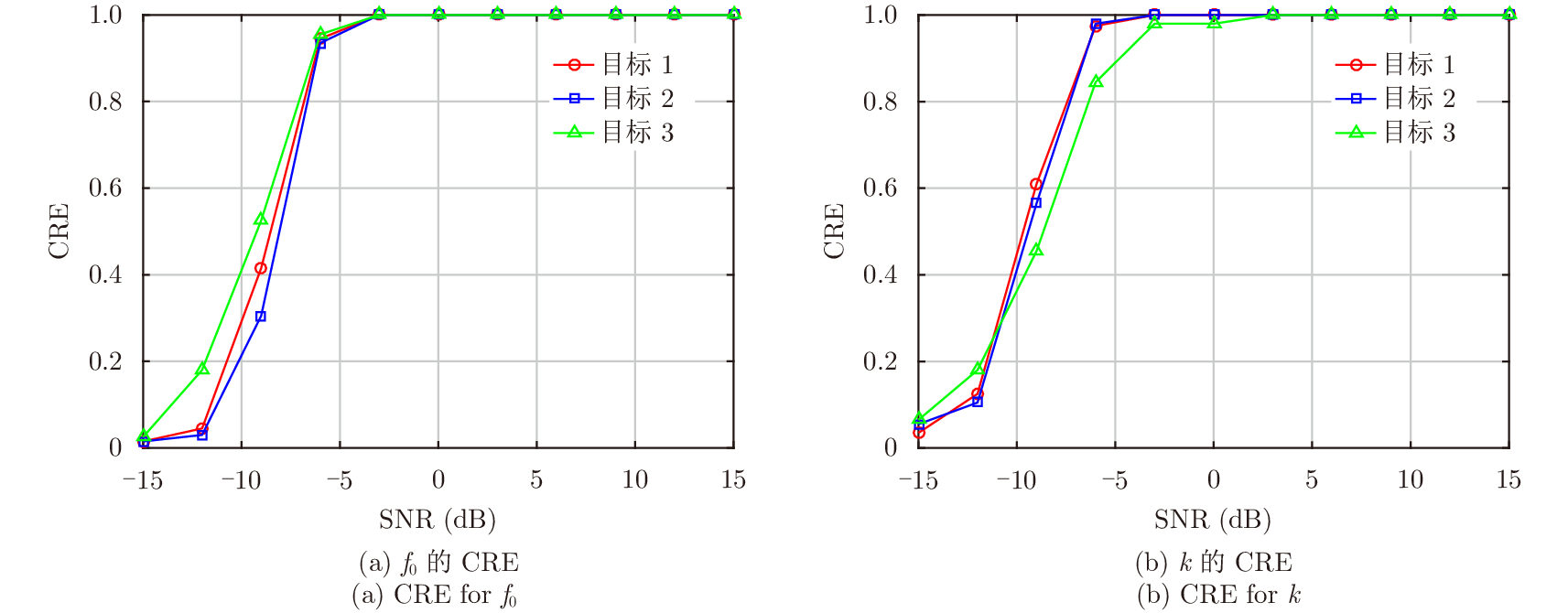
图7表示目标发射信号的初始频率和调频斜率的估计准确率随信噪比的变化曲线。由图7可知,在信噪比低于
|
图 7 目标信号参数的CRE Fig.7 CRE for signal parameters |
针对多个未知LFM信号辐射源,本文提出的DPD-FRFT算法在控制计算量的同时,可有效联合估计出目标位置和信号参数。该算法有益探索了多目标、多基站无源直接定位问题,获得了较好的精度定位。
| [1] |
Amar A and Weiss A J. Localization of narrowband radio emitters based on Doppler frequency shifts[J].
IEEE Transactions on Signal Processing, 2008, 56(11): 5500-5508. DOI:10.1109/TSP.2008.929655 ( 0) 0)
|
| [2] |
贾兴江. 运动多站无源定位关键技术研究[D]. [博士论文], 国防科学技术大学, 2011: 3–42
Jia Xing-jiang. Research on passive location technologies of multiple moving observers[D]. [Ph.D. dissertation], National University of Defense Technology, 2011: 3–42 (  0) 0)
|
| [3] |
Tirer T and Weiss A J. High resolution localization of narrowband radio emitters based on Doppler frequency shifts[J].
Signal Processing, 2017, 141: 288-298. DOI:10.1016/j.sigpro.2017.06.019 ( 0) 0)
|
| [4] |
赵勇胜, 赵拥军, 赵闯. 联合角度和时差的单站无源相干定位加权最小二乘算法[J].
雷达学报, 2016, 5(3): 302-311. Zhao Yong-sheng, Zhao Yong-jun, and Zhao Chuang. Weighted least squares algorithm for single-observer passive coherent location using DOA and TDOA measurements[J]. Journal of Radars, 2016, 5(3): 302-311. DOI:10.12000/JR15133 (  0) 0)
|
| [5] |
Weiss A J. Direct position determination of narrowband radio frequency transmitters[J].
IEEE Signal Processing Letters, 2004, 11(5): 513-516. DOI:10.1109/LSP.2004.826501 ( 0) 0)
|
| [6] |
Yi W, Chen Z H, Hoseinnezhad R, et al. Joint estimation of location and signal parameters for an LFM emitter[J].
Signal Processing, 2017, 134: 100-112. DOI:10.1016/j.sigpro.2016.11.014 ( 0) 0)
|
| [7] |
Oispuu M and Nickel U. Direct detection and position determination of multiple sources with intermittent emission[J].
Signal Processing, 2010, 90(12): 3056-3064. DOI:10.1016/j.sigpro.2010.05.010 ( 0) 0)
|
| [8] |
Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform[J].
IEEE Transactions on Signal Processing, 1996, 44(9): 2141-2150. DOI:10.1109/78.536672 ( 0) 0)
|
| [9] |
Saxena R and Singh K. Fractional Fourier transform: A novel tool for signal processing[J].
Journal of the Indian Institute of Science, 2005, 85(1): 11-26. ( 0) 0)
|
| [10] |
Namias V. The fractional order Fourier transform and its application to quantum mechanics[J].
IMA Journal of Applied Mathematics, 1980, 25(3): 241-265. DOI:10.1093/imamat/25.3.241 ( 0) 0)
|
| [11] |
田瑞琦, 鲍庆龙, 王丁禾, 等. 基于FRFT与Keystone变换的运动目标参数估计算法[J].
雷达学报, 2014, 3(5): 511-517. Tian Rui-qi, Bao Qing-long, Wang Ding-he, et al. An algorithm for target parameter estimation based on fractional Fourier and Keystone transforms[J]. Journal of Radars, 2014, 3(5): 511-517. DOI:10.3724/SP.J.1300.2014.14058 (  0) 0)
|
| [12] |
Almeida L B. The fractional Fourier transform and time-frequency representations[J].
IEEE Transactions on Signal Processing, 1994, 42(11): 3084-3091. DOI:10.1109/78.330368 ( 0) 0)
|
| [13] |
吴超楠. 基于分数阶傅里叶变换的高精度线性调频信号参数估计方法[D]. [硕士论文], 华南理工大学, 2014: 15–63
Wu Chaonan. High-precision parameter estimation for LFM signal based on fractional Fourier transform[D]. [Master dissertation], South China University of Technology, 2014: 15–63 (  0) 0)
|
| [14] |
Schonhoff T A and Giordano A A. Detection and Estimation Theory and its Applications[M]. Upper Saddle River, NJ: Prentice Hall, 2006
( 0) 0)
|
| [15] |
艾越. 分置MIMO雷达多目标信号级定位算法研究[D]. [硕士论文], 电子科技大学, 2015: 19–23
Ai Yue. Research of MIMO radar with widely separated antennas signal level multi-target localization[D]. [Master dissertation], University of Electronic Science and Technology of China, 2015: 19–23 (  0) 0)
|
| [16] |
Schultz R R and Stevenson R L. A Bayesian approach to image expansion for improved definition[J].
IEEE Transactions on Image Processing, 1994, 3(3): 233-242. DOI:10.1109/83.287017 ( 0) 0)
|
| [17] |
Sneath P H A and Sokal R R. Numerical taxonomy: The principles and practice of numerical classification[J].
Taxon, 1963, 12(5): 190-199. ( 0) 0)
|




