(卫星导航电子信息技术教育部重点实验室(北京理工大学) 北京 100081)
(Key Laboratory of Electronic and Information Technology in Satellite Navigation (Beijing Institute of Technology), Ministry of Education, Beijing 100081, China)
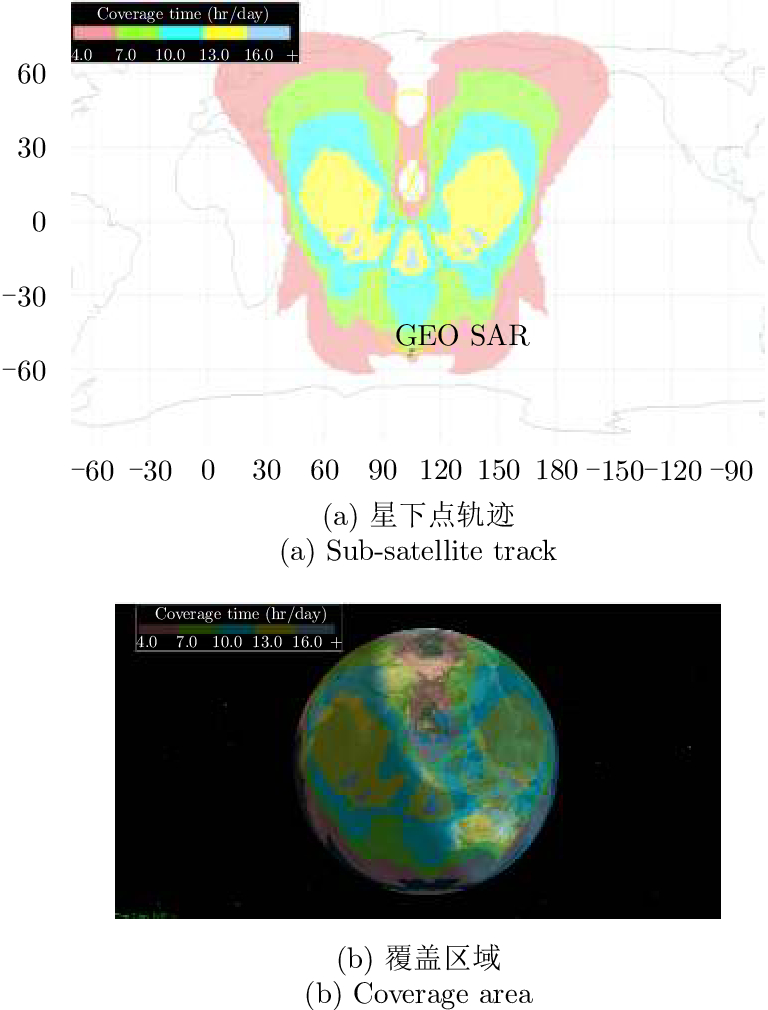
地球同步轨道SAR (GEOsynchronous orbit Synthetic Aperture Radar, GEO SAR)是运行在36000 km高度地球同步轨道上的SAR,这种地球同步轨道并非地球静止轨道,它具有一定的倾斜角度,星下点轨迹为‘8’字形(图1),由此可获得与地面目标的相对运动,实现SAR成像[1–4]。与传统的低轨星载SAR相比,GEO SAR具有重访时间短、观测范围大等不可替代的优点,在灾害预警、海洋监测、军事打击等领域具有重要的应用价值。
|
图 1 GEO SAR星下点轨迹及覆盖区域 Fig.1 The sub-satellite track and coverage area of GEO SAR |
但是,GEO SAR合成孔径时间长、观测范围大,容易受到包括电离层干扰和对流层干扰的大气层效应的影响,造成成像质量下降。早在2000年,加拿大遥感中心的Gray等人基于对Radarsat-1卫星数据的大量研究,指出电离层电子密度的起伏会导致SAR图像出现方位向偏移,影响成像质量[5]。2006年,Meyer针对电离层干扰对SAR系统的影响开展了一系列详细的研究,指出电离层变化会造成距离时延、干涉相位偏差、距离向散焦和法拉第旋转等一系列影响[6,7]。电离层干扰对较低频段和较高发射带宽的SAR系统均会在距离向Chirp信号的边缘带来较大的相位误差[8]。
对流层引入的误差会影响SAR信号的相干性,造成成像质量下降。Sun和Zhang等人利用Hopfield对流层模型和射线描迹法,研究了对流层对星载SAR成像的影响,指出分辨率越高,斜视角越大,影响越严重[9,10];对流层干扰会使干涉和差分干涉相位精度下降,严重降低高程和形变反演精度[11]。而对流层中湍流也会影响电波传播。在2004~2007年间,Dickey等人基于Sandia国家实验室的机载SAR数据,模拟仿真了湍流的影响,他们在图像中观测到了亮度异常的区域,认为这种异常是由于大气折射率扰动引起的。Muschinski等人发现折射率场的变化会在地面形成衍射图案,这与Dickey在机载SAR图像中观测到的亮度异常区域一致,并且说明了对流层扰动对10 GHz以下的电磁波传播影响基本可忽略,而对22~60 GHz的电磁波影响最明显[12]。
在大气层效应对GEO SAR影响研究方面,Hobbs等人研究了GEO SAR系统中各种因素对系统性能的影响,提出影响GEO SAR成像的3个至关重要因素:地球潮汐、对流层扰动和电离层扰动[13–15]。他指出电离层扰动是GEO SAR成像中的主要问题,提出了自聚焦算法,该算法在解决电离层扰动问题方面具有重要的潜力。Monti-Guarnieri和Broquetas等人研究了近零倾角GEO SAR的系统设计和性能分析,并利用Ku波段实现每隔5 min以接近300 m的分辨率对6000 km2区域的水汽情况进行监测,同时,利用反演的水汽情况进行大气误差补偿以完成精确高分辨率成像[16–18]。此外,Monti-Guarnieri等人还提出了一发多收的GEMINI系统(Geosynchronous Earth Monitoring by INterferometry and Imaging)和多发多收的ARGOS系统(Advanced Radar Geosynchronous Observation System),用以提高大气误差的估计精度和高分辨成像性能[19,20]。Monti-Guarnieri等人还定量评估了时空变湍流对GEO SAR聚焦的影响,提出一种整合了大气相位屏(Atmospheric Phase Screen, APS)的估计与补偿的新型聚焦方法[21]。
针对GEO SAR中大气层效应影响严重的问题,北京理工大学研究人员在GEO SAR大气层效应方面也开展了大量研究工作,并建立了时空变大气层模型,分析了其对长孔径时间、大观测范围的GEO SAR的影响,指出在L波段电离层的影响十分严重,并提出了相应的补偿算法[22–31];此外,开展了基于导航卫星的电离层实验,验证了理论分析。中科院电子所分析了对流层对L波段圆迹GEO SAR(GEOsynchronous orbit Circular Synthetic Aperture Radar, GEOCSAR)成像的影响,并基于对流层实测数据仿真分析了24 h内对流层变化对L波段GEOCSAR成像的影响,在对流层效应影响下成像结果出现了轻微散焦现象,同时存在大约2 m的方位向图像偏移[32,33]。国防科技大学结合最新的电离层和对流层相关数据也分别对GEO SAR中对流层湍流和电离层不规则体进行了建模和影响分析,该模型可以用作GEO SAR原始数据的仿真和评估[34,35]。
在GEO SAR中,大气层效应存在时空变化特性,引入相位误差并在合成孔径时间内积累,从而影响成像质量;在成像场景内不同位置的目标所受影响不同,也会造成图像畸变。因此,针对GEO SAR中大气层效应的影响,本文分别对对流层和电离层的建模和影响分析进行了总结。全文组织如下:首先,给出了大气层效应影响的模型;然后,构建了考虑大气层效应的精确GEO SAR信号模型;最后,对常规对流层、对流层湍流、背景电离层、电离层闪烁的影响分别进行了理论分析和数据仿真。
2 大气层效应建模 2.1 对流层误差建模对流层对电波传播的影响可分为常规对流层和对流层湍流两部分。常规对流层主要指对流层的缓变部分。电波在对流层中的传播特性可用折射率表征。当信号穿越对流层时,由于折射率不为1,传播速度会减慢,引入时延误差;且对流层中大气温度、压力和湿度等气象要素随高度发生变化,折射率的空间分布会存在不均匀性,因此传播路径发生弯曲,造成弯曲误差。对流层湍流是指在某些突发和极端气象条件下,大气温度、压力和湿度等气象要素出现剧烈变化,引起对流层折射率的快速波动,导致信号幅度和相位发生随机起伏。
2.1.1 常规对流层对流层的电波传播特性通常用折射率N表示[36],其定义为:
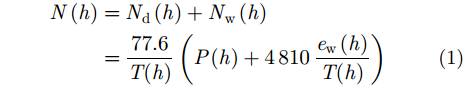
|
其中,
由于对流层折射率不再为1,当雷达信号穿越对流层时,传播速度会减慢,且由于其空间分布的不均匀性,传播路径还会发生弯曲。因此,当GEO SAR信号穿越对流层时,会产生时延误差和弯曲延迟,引入相位误差。根据射线描迹法和Snell定律,在球面分层假设下,对流层误差
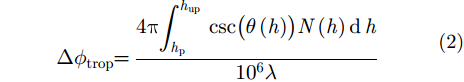
|
其中,
对流层湍流会造成折射指数的随机起伏,其功率谱服从幂律谱分布,可采用Kolmogorov-Von-Karman谱[37],即
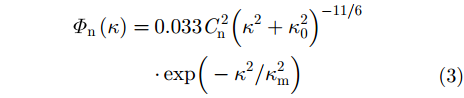
|
其中,
折射指数功率谱与其造成的相位功率谱
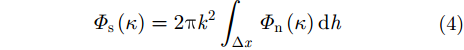
|
其中,
在相位屏仿真中,首先用大气相位扰动的功率谱函数即
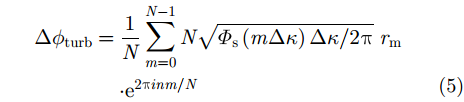
|
其中,
电离层中充满自由电子,造成电离层折射率变化,进而会引起穿越其中的电波信号出现传播速度变化,引入时延误差。电离层对电波传播的影响可分为大尺度的背景电离层和中小尺度的电离层闪烁。
2.2.1 背景电离层设背景电离层折射率为
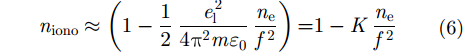
|
其中,
由于电离层折射率不为1,因此信号在穿越电离层时会产生时延,时延误差可通过折射率的路径积分获得。考虑GEO SAR信号的双程传播,电离层引入的相位误差为:
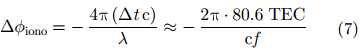
|
其中,定义
电离层闪烁可由闪烁采样模型表示,其幅度起伏服从Nakagami-m分布,相位起伏服从高斯分布;而其幅度功率谱
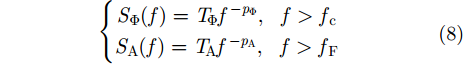
|
其中,菲涅耳频率
在截止频率之后,闪烁幅度谱和相位谱才表现出一定的幂律特性,一般地,对于幅度闪烁功率谱,菲涅尔频率与卫星运动速度和不规则体的漂移速度有关,大约在0.1 Hz–几Hz左右。对于相位谱功率谱,截止频率与电离层相位闪烁信号的去相关时间关系密切。由于一般电离层闪烁信号的去相关时间为1~2 s,相位闪烁信号的能量出现在大约0.1 Hz频率之后。此外,电离层幅相闪烁信号之间也存在一定的负相关性,一般负相关系数在–0.6左右。
3 GEO SAR信号建模GEO SAR合成孔径时间可达百秒到千秒量级,因此需要考虑在孔径时间内大气状态随时间的变化对成像的影响;同时,GEO SAR覆盖范围可达数百到数千公里,因此需要考虑观测场景内大气状态随空间的变化对成像的影响。
时空变大气层对穿越其中的信号引入的相位误差可表示为:
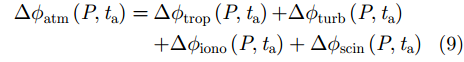
|
其中,P表示场景内不同位置处目标;
GEO SAR精确回波信号可表示为:
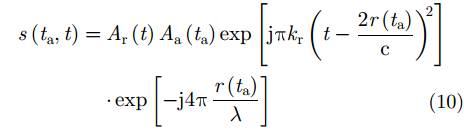
|
其中,
由于电离层为色散介质,其引入的相位误差与信号频率有关,因此将信号变换到距离向频域,并叠加大气层效应引入的相位误差,表示为:
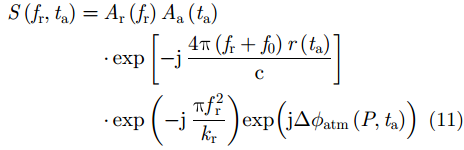
|
对流层为非色散介质,对信号不同频率影响一致,因此不会影响距离向成像。然而,对流层的时变性以及不同PRT时数据获取几何关系的差异,导致时延误差不同,影响方位向成像。因此此处仅对GEO SAR方位向信号进行分析,此时考虑对流层变化的方位向信号可写为:
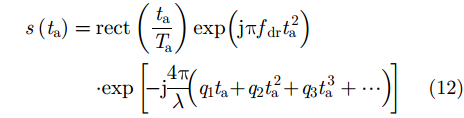
|
其中,
通过级数反转理论和傅里叶变换方法,推导方位向信号频谱可得
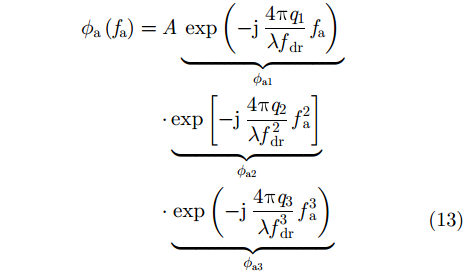
|
在式(13)中,对流层延迟随时间的线性变化部分
相位
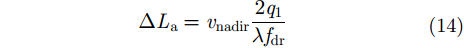
|
可以看出,当GEO SAR数据获取几何关系固定时(即
方位向2次相位误差
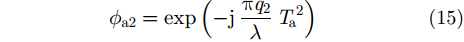
|
可以看出,信号波长越小、对流层延迟随时间的2阶变化率越大、合成孔径时间越长,对流层引起的2次相位误差也越大,影响越严重。
方位向3次相位误差
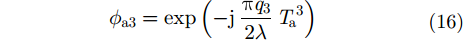
|
可以看出,信号波长越小、对流层延迟随时间的3阶变化率越大、合成孔径时间越长,对流层引起的3次相位误差也越大。
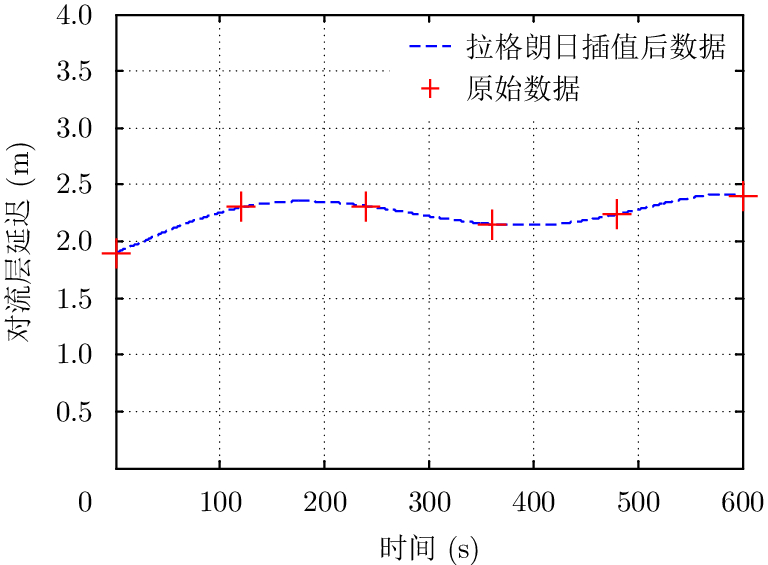
在本节中,我们将利用对流层实测数据完成常规对流层对GEO SAR成像的影响分析。大气折射率廓线数据由中国国家卫星气象中心发布。该数据是由风云三号C星(FY-3C卫星)测量获得,时间间隔通常为2~5 min,包括大气折射率数值、数据时间(年/月/日/时/分/秒)以及卫星位置坐标。选取2015年5月27日18:28到18:40的数据进行分析,数据间隔为2 min,在12 min时间里共有6组数据。使用射线描迹法求出这6组折射率数据对应的信号延迟,如图2中红色“+”所示。由于这6组数据间隔为120 s,因此我们通过拉格朗日插值,计算出每一秒时刻的对流层延迟量,如图2所示。
|
图 2 基于大气折射率廓线数据获得的对流层信号延迟 Fig.2 Tropospheric signal delays based on atmospheric refractive index profile data |
FY-3C是低轨卫星,因此图2中的信号延迟仅能代表FY-3C卫星信号传播路径上的大气状态,并不能完全反映对流层对GEO SAR信号的影响。因此,需要根据GEO SAR卫星和FY-3C卫星轨道参数进行等效处理[3],计算GEO SAR信号传播路径上的对流层延迟数据如表1所示。
| 表 1 GEO SAR对流层延迟的各阶时间变化情况 Tab.1 Temporal variability of each order of GEO SAR tropospheric delay |
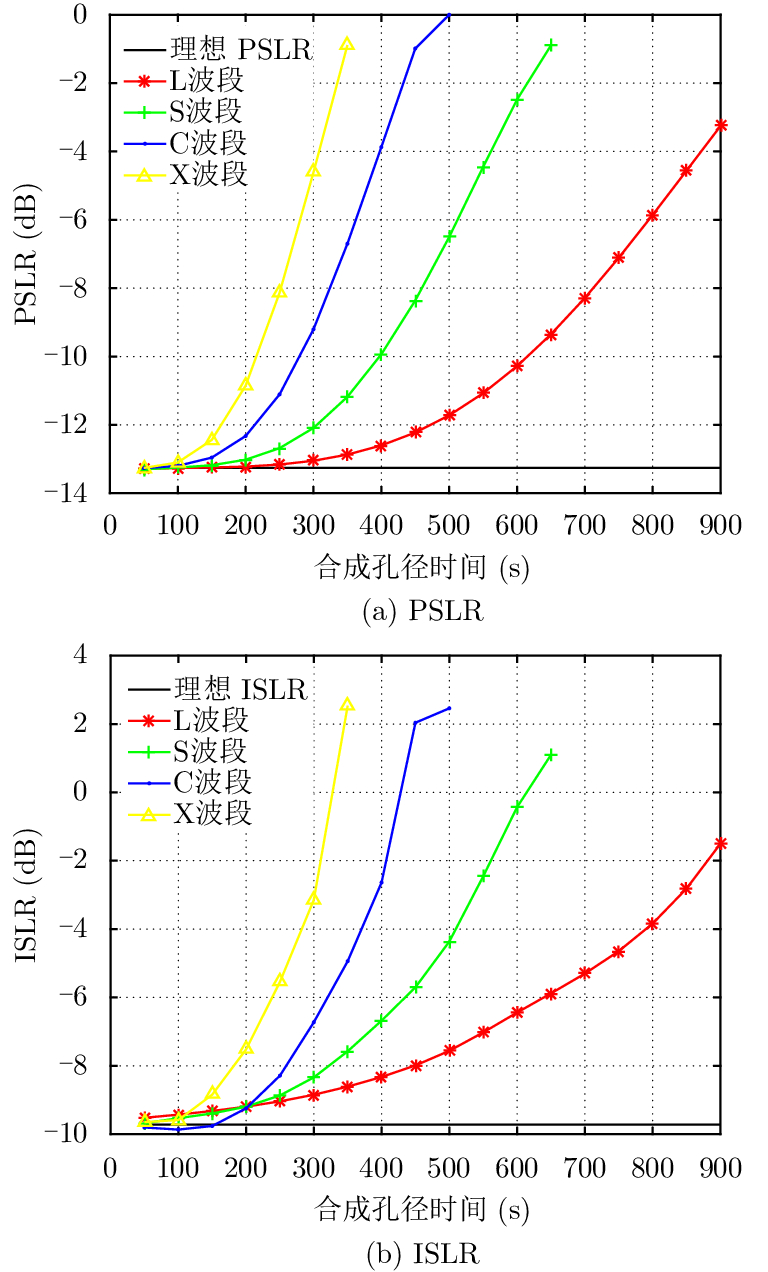
对流层对GEO SAR成像的影响与积累时间相关。虽然对流层为非色散介质,不影响距离向成像,但在方位向成像处理时,不同波长GEO SAR的累积相位误差不同。因此,分别对L, S, C, X波段进行了仿真比较。评估结果如图3所示。对流层误差在长积累时间情况下会造成图像散焦。波长越小,影响越大。而对流层的变化也会造成方位向图像偏移,该偏移与波段和积累时间无关,仅取决于对流层的线性变化率。
|
图 3 不同波段、不同积累时间下对流层对GEO SAR成像影响的评估结果 Fig.3 Results of tropospheric GEO SAR imaging at different wave bands and different integrate times |
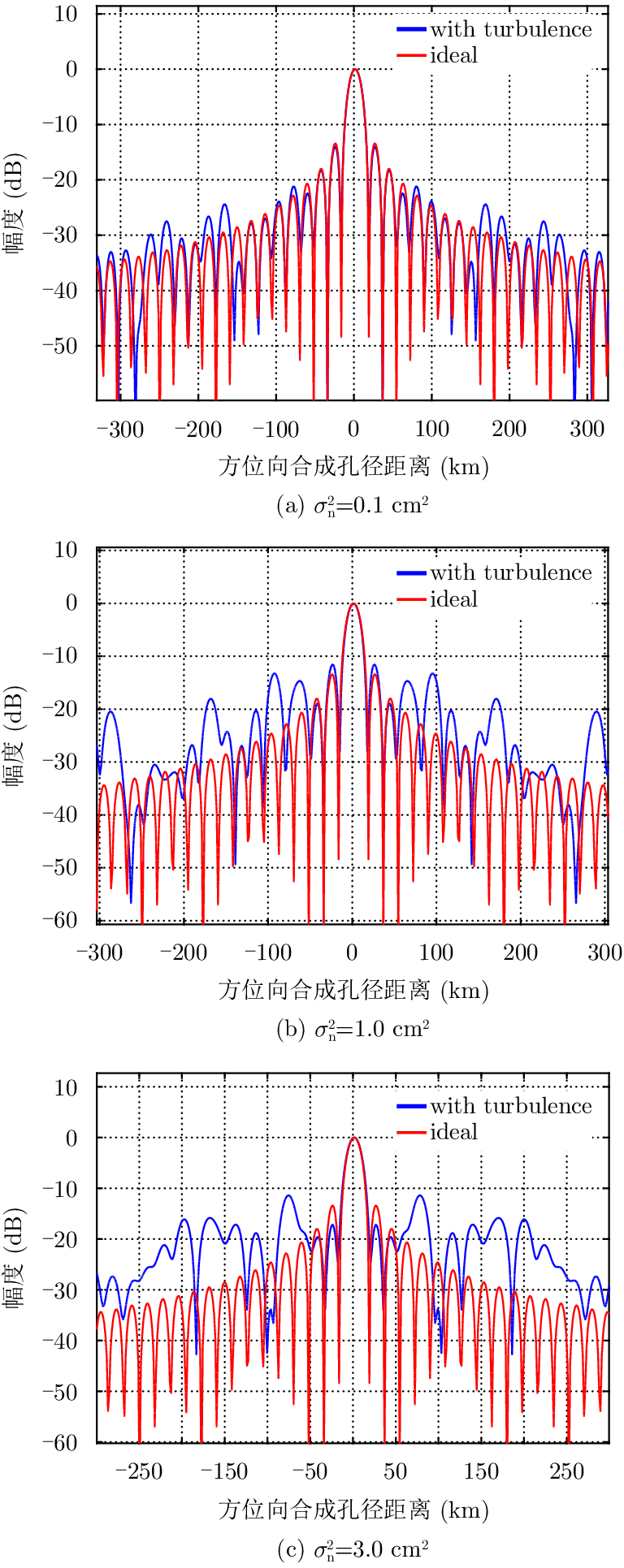
对流层湍流会造成信号的幅相起伏,造成GEO SAR的成像质量下降。湍流强度越大,峰值旁瓣比(Peak SideLobe Ratio, PSLR)和积分旁瓣比(Integral SideLobe Ratio, ISLR)恶化越严重。令
|
图 4 100 s下 L波段方位向包络图 Fig.4 L-band azimuth envelope at 100 s |
由图4看出,当
背景电离层TEC随时间的变化是个缓变的过程,可表示为慢时间
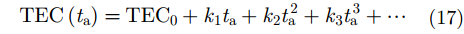
|
其中,
电离层为色散介质,会影响距离向成像,分析方法与传统低轨SAR相同。影响距离向成像的主要是背景电离层TEC中的恒定值
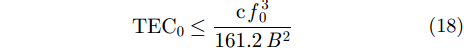
|
考虑L波段信号和20 m分辨率对应的信号带宽,
在本节中将具体分析随时间变化TEC对GEO SAR方位向成像的影响,方位向信号可表示为:
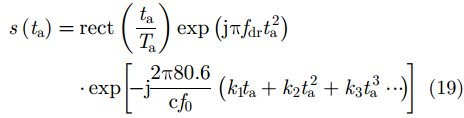
|
类似地,采用级数反转理论和傅里叶变换方法[39,40]得到方位向信号频谱
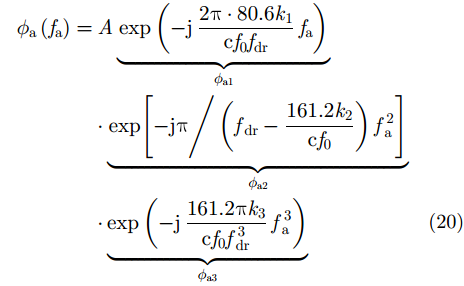
|
在式(20)中,TEC随时间的线性变化部分
相位
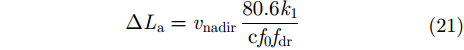
|
其中,
相位
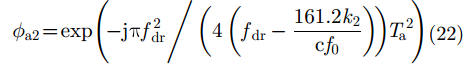
|
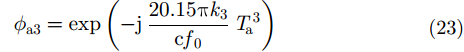
|
可以看出,信号频率越低,TEC随时间的2阶变化率、3阶变化率越大,合成孔径时间越长,电离层引起的方位向2次和3次相位误差也越大,对成像影响越严重。
在本节中,我们将利用美国国家海洋和大气管理局提供的美国电离层垂直TEC数据(US-TEC)进行分析。该数据具有空间间隔小(每1个经纬度1个数据)、时间间隔小(每15 min 1个数据)、精度高(数据误差不超±0.1 TECU)的特点。我们选择美国中部堪萨斯地区(39.40°N, 98.80°W)的数据作为研究对象,并结合GEO SAR卫星轨道参数将垂直TEC数据转化成GEO SAR卫星信号传播路径上的TEC数据,同时对数据进行拉格朗日插值处理,从而获得1000 s时间内GEO SAR信号传播路径上的TEC数据,并构建受电离层影响的GEO SAR回波信号,仿真分析不同合成孔径时间下电离层对L波段GEO SAR成像的影响。经过预处理可得TEC各阶变化率如表2所示。
| 表 2 电离层TEC随时间变化情况 Tab.2 Rate of ionospheric TEC changing with time |
基于前述理论分析可知,合成孔径时间越长,电离层对GEO SAR聚焦影响越大。在仿真时,信号频率为1.25 GHz,信号带宽为20 MHz,分别设置合成孔径时间为100 s, 300 s和500 s。点目标成像的评估结果如表3所示,电离层会引起GEO SAR成像结果出现大约4.3 m的方位向图像偏移;同时,随着合成孔径时间的增大,方位向峰值旁瓣比(PSLR)变得越来越差,而距离向成像尚未受到电离层的影响。
| 表 3 背景电离层对GEO SAR成像影响评估结果 Tab.3 Results of GEO SAR imaging effected by background ionosphere |
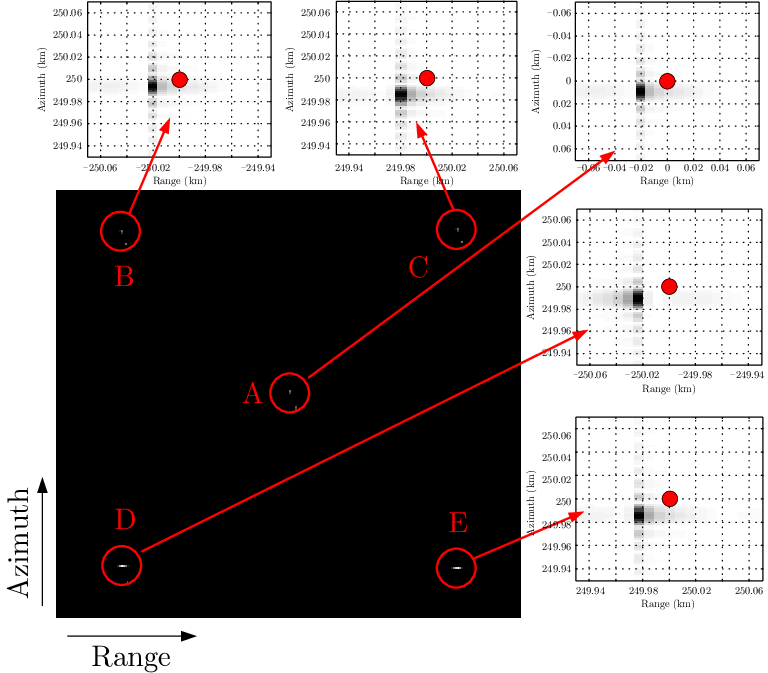
电离层空变性表现为大成像场景内不同位置处电离层TEC的变化,可利用点阵目标进行仿真。点阵中各点经纬度分别设置为:A(116.30°E, 39.90°N), B(114.00°E, 42.20°N), C(118.60°E, 42.20°N), D(114.00°E, 37.60°N), E(118.60°E, 37.60°N),不同位置处的TEC可通过Klobuchar模型计算得到。点阵目标仿真结果如图5所示。
|
图 5 点阵目标成像结果 Fig.5 Lattice targets imaging results |
从图5仿真结果可以看出,在该电离层状态下没有出现散焦,仅出现了图像偏移。但是由于不同位置处TEC不同,因此偏移程度也不同。图像沿着距离向的最小偏移量为C点的19.5 m,偏移量最大的为D点的25.0 m;同时,图像沿着方位向的最小偏移量为B点的9.0 m,偏移量最大的为C点的16.0 m。由此可见,电离层空变性会造成图像扭曲,必须予以考虑。
4.2.2 电离层闪烁[29]基于SPECAN算法,受电离层闪烁影响的信号聚焦后可表示为:
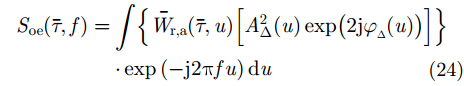
|
其中,
当电离层闪烁较弱时,并且忽略较小的联合项,根据卷积定理,可以近似得到点扩展函数
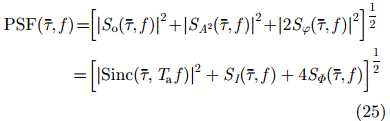
|
其中,
在GEO SAR中,系统分辨率远小于幂律谱的菲涅耳频率,则幅度闪烁的增强会导致GEO SAR方位向分辨率有一定程度的恶化,但由于幅度谱的强能量干扰位置距离主瓣较远,所以分辨率的恶化随幅度闪烁的增强并不明显,表示为:
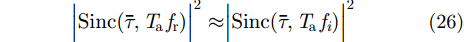
|
类似的,GEO SAR在电离层闪烁影响下ISLR和PSLR表示为:
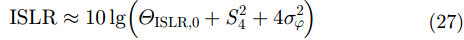
|
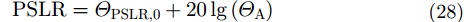
|
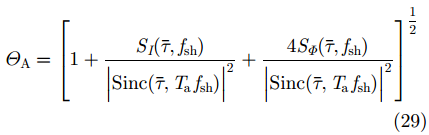
|
其中,
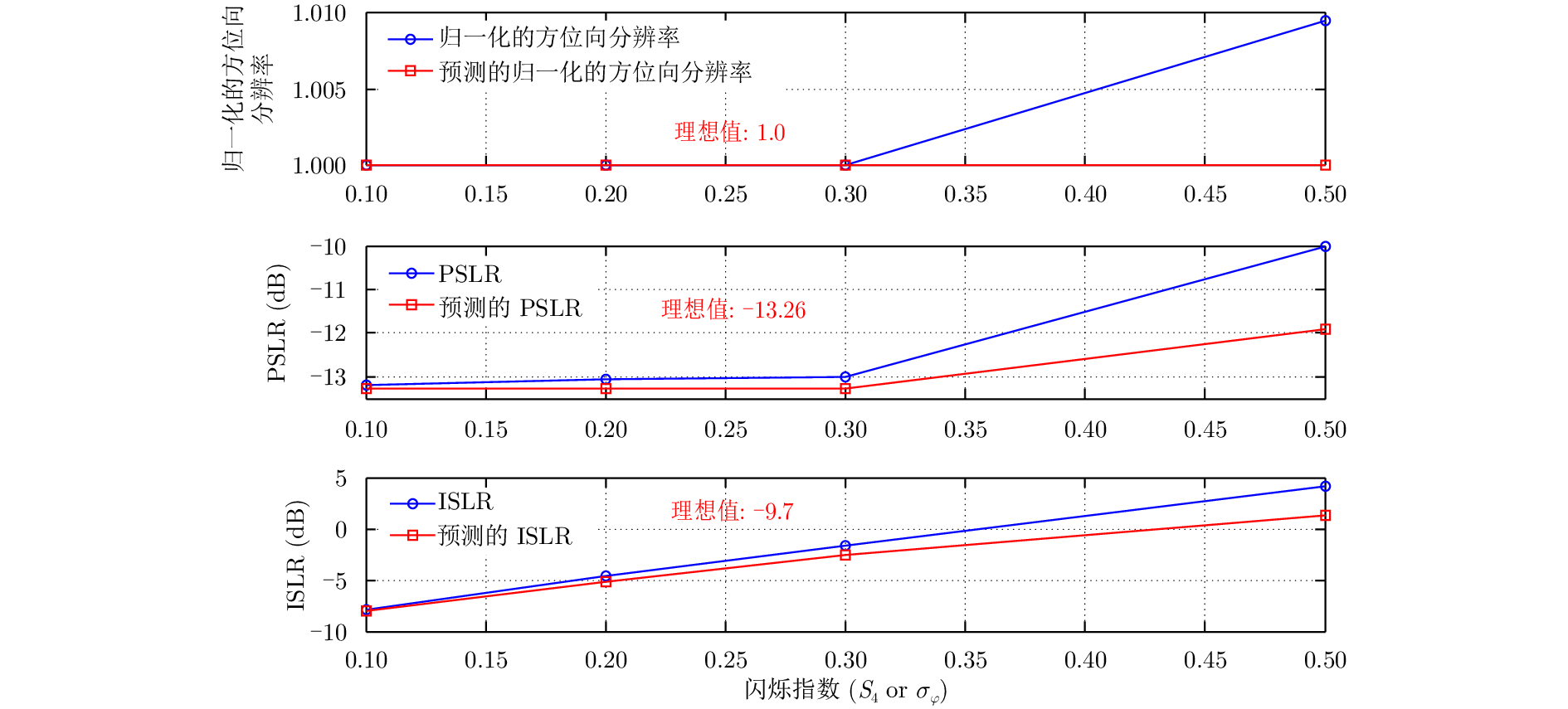
电离层闪烁对GEO SAR成像的影响可通过式(27)进行理论评估。不同强度电离层闪烁影响下,点目标的成像质量评价指标如图6所示。
|
图 6 电离层闪烁影响下成像指标参数分析 Fig.6 Analysis of imaging quality parameters in the presence of ionospheric scintillation |
根据上述结果可知,电离层闪烁强度越大,方位向分辨率展宽不明显。因此分辨率的分析和仿真结果有较好的一致性。在中等闪烁强度下,中等闪烁时,由于仿真时低频区域能量的泄露,方位向的分辨率才有一定的恶化,但可以忽略。
方位向PSLR会随着闪烁的增强而恶化但不明显。这是由于在主瓣附近低频区域对应的闪烁信号功率谱能量为零,所以在较小闪烁强度的情况下,PSLR几乎一致保持在一个比较稳定的良好状态。与分辨率的情况类似,PSLR的轻微恶化也是由于仿真时低频区域能量的泄露产生的。
但是,方位向积分旁瓣比ISLR会随着电离层闪烁的增强而严重恶化。对比真实的ISLR和理论预测的ISLR可以发现,电离层闪烁强度越小,越符合理论分析的近似条件,结果吻合越好。当S4=0.3,
大气层效应对GEO SAR干涉/差分干涉的影响主要是由背景电离层引入的干涉相位屏误差产生的。根据文献[27],时空变背景电离层引入的干涉相位屏误差
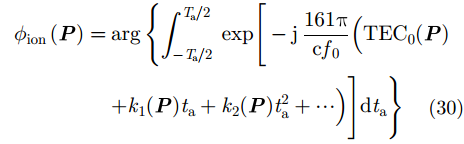
|
一般地,由于TEC 3阶以上的变化产生的影响均在0.01 TECU以下(TEC 3阶变化率一般在10–10~10–8量级,积累后在0.01 TECU以下),因此,忽略它们的影响,可以得到空变背景电离层引入的干涉相位屏误差表示为:
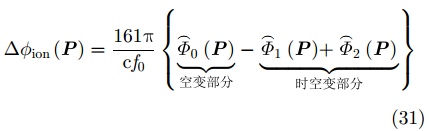
|
其中,
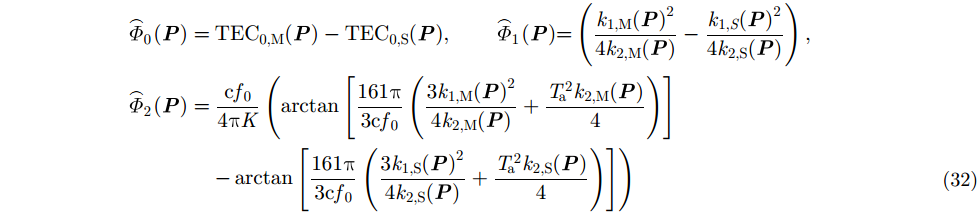
|
其中,
上述模型中不只包含“冻结模型”下空变的背景电离层影响导致的相位项
最终,背景电离层变化产生的干涉相位屏误差
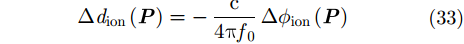
|
我们利用美国背景电离层进行验证。实验中选取的TEC数据区域位于纬度200°N–500°N,经度600°W–1400°W。TEC的1阶和2阶变化率可以由多次时间采样的TEC数据进行2阶或更高阶拟合获得。我们选取的观测场景为以太平洋上的Isla Guadalupe岛(29.02°N, 118.27°W)为中心的一个超过1000 km×1000 km的区域。考虑GEO D-InSAR系统具有快速重访能力的系统特点,我们选取间隔1天的GEO SAR卫星重轨干涉轨道数据进行后面的仿真。仿真中采用干涉对数据的干涉基线为大约1.3 km。系统信号发射带宽为18 MHz,积累时间为250 s。选取的TEC数据分别于UTC时间2013年10月7日22:00–23:00和UTC时间2013年10月08日22:00–23:00获得,对应于本地时间为中午到傍晚的时间段内,覆盖TEC数值的日变化和变化率的峰值区间,具有较大的常数TEC值和相对变化率,这将有利于分析相对应背景电离层随时间变化产生的影响。
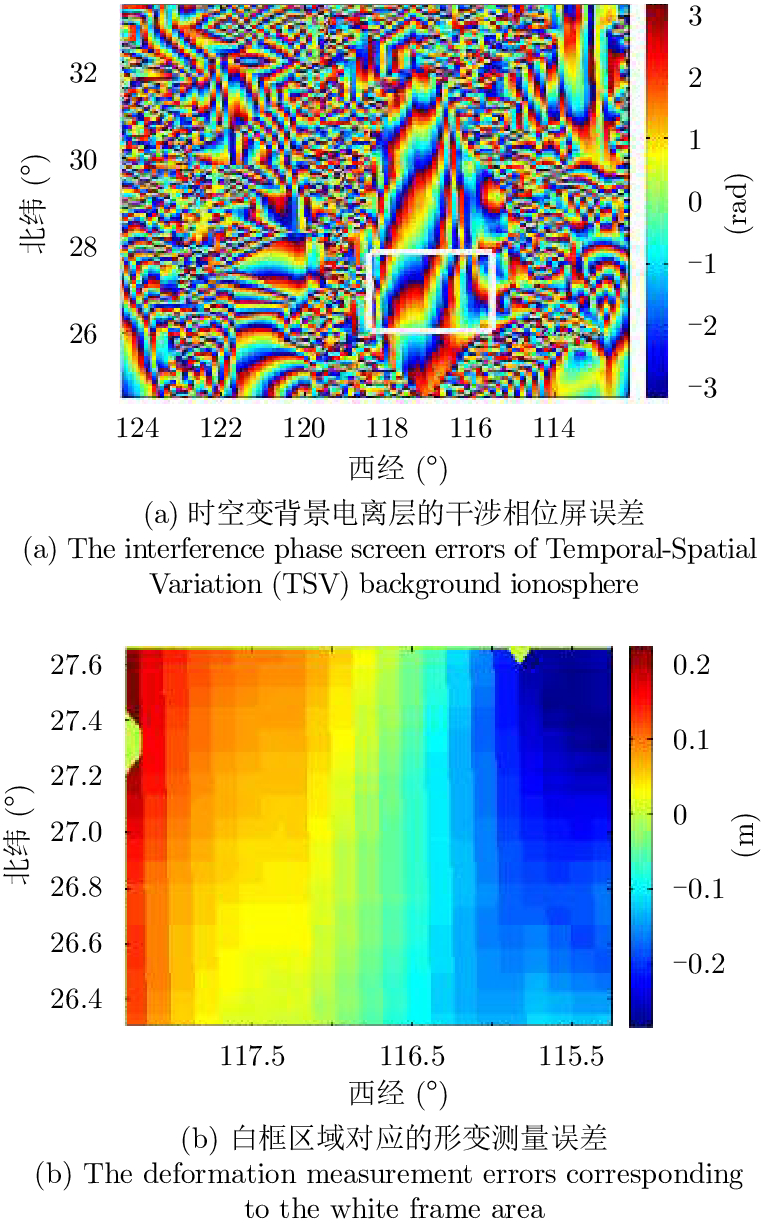
根据建立的模型和美国背景电离层数据,获得了时空变背景电离层的时空变部分
|
图 7 时空变电离层引入的干涉相位屏误差和评估 Fig.7 The interference phase screen errors and evaluation introduced by TSV ionosphere |
GEO SAR具有合成孔径时间长、观测范围大的特性,因此,大气层的时空变化会导致GEO SAR成像性能下降,甚至散焦。在合成孔径时间内,大气层状态的缓慢变化或快速随机扰动,会引入相位误差,造成方位向散焦;在观测范围内,不同位置处大气状态各异,成像影响也不尽相同。
本文对对流层和电离层建模和影响分析的研究进行了总结。针对常规对流层和背景电离层等大气层缓变部分,建立时频混合GEO SAR信号模型,分析了不同时间变化率对成像的影响;针对对流层湍流和电离层闪烁等随机扰动造成的影响,利用幂律功率谱模型,仿真并分析了长孔径时间内随机误差的影响。背景电离层会造成图像偏移、图像散焦,电离层状态的空变性会造成图像畸变。此外,时空变背景电离层变化还会显著地使差分干涉处理的形变反演精度严重下降;电离层闪烁会影响方位向成像,主要造成ISLR的升高。在L波段,GEO SAR受电离层影响较为严重,必须予以补偿。对流层也主要影响方位向成像,但在L波段影响较小,仅当积累时间达到数百秒时需要考虑;而当频率升高时,如X波段,对流层影响变得严重,需要予以考虑。
| [1] |
Tomiyasu K. Synthetic aperture radar in geosynchronous orbit[C]. Proceedings of 1978 Antennas and Propagation Society International Symposium, Washington, DC, USA, 1978: 42–45
( 0) 0)
|
| [2] |
Tomiyasu K and Pacelli J L. Synthetic aperture radar imaging from an inclined geosynchronous orbit[J].
IEEE Transactions on Geoscience and Remote Sensing, 1983, 21(3): 324-329. DOI:10.1109/TGRS.1983.350561 ( 0) 0)
|
| [3] |
NASA and JPL. Global earthquake satellite system: A 20-year plan to enable earthquake prediction[EB/OL]. http://solidearth.jpl.nasa.gov/GESS/3123_GESS_Rep_2003.pdf, 2015, 9
( 0) 0)
|
| [4] |
Edelstein W N, Madsen S N, Moussessian A, et al.. Concepts and technologies for synthetic aperture radar from MEO and geosynchronous orbits[C]. Proceedings of SPIE 5659, Enabling Sensor and Platform Technologies for Spaceborne Remote Sensing, Honolulu, Hawaii, 2005: 195–203
( 0) 0)
|
| [5] |
Laurence Gray A, Mattar K E, and Sofko G. Influence of ionospheric electron density fluctuations on satellite radar interferometry[J].
Geophysical Research Letters, 2000, 27(10): 1451-1454. DOI:10.1029/2000GL000016 ( 0) 0)
|
| [6] |
Meyer F, Bamler R, Jakowski N, et al. The potential of low-frequency SAR systems for mapping ionospheric TEC distributions[J].
IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 560-564. DOI:10.1109/LGRS.2006.882148 ( 0) 0)
|
| [7] |
Meyer F J and Nicoll J. The impact of the ionosphere on interferometric SAR processing[C]. Proceedings of 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 2008: II-391–II-394
( 0) 0)
|
| [8] |
Meyer F J. Performance requirements for ionospheric correction of low-frequency SAR data[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3694-3702. DOI:10.1109/TGRS.2011.2146786 ( 0) 0)
|
| [9] |
Sun J P, Bi Y K, Wang Y P, et al.. High resolution SAR performance limitation by the change of tropospheric refractivity[C]. Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011
( 0) 0)
|
| [10] |
Zhang F, Li G J, Li W, et al. Multiband microwave imaging analysis of ionosphere and troposphere refraction for spaceborne SAR[J].
International Journal of Antennas and Propagation, 2014, 2014: 913056 ( 0) 0)
|
| [11] |
Hanssen R F. Radar Interferometry: Data Interpretation and Error Analysis[M]. Dordrecht: Kluwer Academic Publishers, 2001
( 0) 0)
|
| [12] |
Danklmayer A, Doring B J, Schwerdt M, et al. Assessment of atmospheric propagation effects in SAR images[J].
IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(10): 3507-3518. DOI:10.1109/TGRS.2009.2022271 ( 0) 0)
|
| [13] |
Hobbs S, Mitchell C, Forte B, et al. System design for geosynchronous synthetic aperture radar missions[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7750-7763. DOI:10.1109/TGRS.2014.2318171 ( 0) 0)
|
| [14] |
Bruno D and Hobbs S E. Radar imaging from geosynchronous orbit: Temporal decorrelation aspects[J].
IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 2924-2929. DOI:10.1109/TGRS.2010.2042062 ( 0) 0)
|
| [15] |
Bruno D, Hobbs S E, and Ottavianelli G. Geosynchronous synthetic aperture radar: Concept design, properties and possible applications[J].
Acta Astronautica, 2006, 59(1–5): 149-156. DOI:10.1016/j.actaastro.2006.02.005 ( 0) 0)
|
| [16] |
Ruiz Rodon J, Broquetas A, Guarnieri A M, et al. Geosynchronous SAR focusing with atmospheric phase screen retrieval and compensation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(8): 4397-4404. DOI:10.1109/TGRS.2013.2242202 ( 0) 0)
|
| [17] |
Ruiz-Rodon J, Broquetas A, Makhoul E, et al. Nearly zero inclination geosynchronous SAR mission analysis with long integration time for earth observation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6379-6391. DOI:10.1109/TGRS.2013.2296357 ( 0) 0)
|
| [18] |
Guarnieri A M, Rocca F, and Ibars A B. Impact of atmospheric water vapor on the design of a Ku band geosynchronous SAR system[C]. Proceedings of 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009
( 0) 0)
|
| [19] |
Guarnieri A M, Tebaldini S, Rocca F, et al.. GEMINI: Geosynchronous SAR for earth monitoring by interferometry and imaging[C]. Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012
( 0) 0)
|
| [20] |
Monti Guarnieri A, Broquetas A, Recchia A, et al. Advanced radar geosynchronous observation system: ARGOS[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(7): 1406-1410. DOI:10.1109/LGRS.2015.2404214 ( 0) 0)
|
| [21] |
Monti Guarnieri A, Leanza A, Recchia A, et al. Atmospheric phase screen in GEO-SAR: Estimation and compensation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(3): 1668-1679. DOI:10.1109/TGRS.2017.2766084 ( 0) 0)
|
| [22] |
Hu C, Long T, Zeng T, et al. The accurate focusing and resolution analysis method in geosynchronous SAR[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3548-3563. DOI:10.1109/TGRS.2011.2160402 ( 0) 0)
|
| [23] |
Hu C, Tian Y, Yang X P, et al. Background ionosphere effects on geosynchronous SAR focusing: Theoretical analysis and verification based on the BeiDou Navigation Satellite System (BDS)[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(3): 1143-1162. DOI:10.1109/JSTARS.2015.2475283 ( 0) 0)
|
| [24] |
Dong X C, Hu C, Tian Y, et al. Experimental study of ionospheric impacts on geosynchronous SAR using GPS signals[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2171-2183. DOI:10.1109/JSTARS.2016.2537401 ( 0) 0)
|
| [25] |
Tian Y, Hu C, Dong X C, et al.. Analysis of effects of time variant troposphere on geosynchronous SAR imaging[C]. Proceedings of 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2016: 5051–5054
( 0) 0)
|
| [26] |
田野, 董锡超, 胡程. 对流层对地球同步轨道SAR成像的影响研究[J].
信号处理, 2015, 31(12): 1562-1567. Tian Ye, Dong Xi-chao, and Hu Cheng. Analysis of troposphere impacts on geosynchronous SAR imaging[J]. Journal of Signal Processing, 2015, 31(12): 1562-1567. DOI:10.3969/j.issn.1003-0530.2015.12.003 (  0) 0)
|
| [27] |
Tian Y, Hu C, Dong X C, et al. Theoretical analysis and verification of time variation of background ionosphere on geosynchronous SAR imaging[J].
IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 721-725. DOI:10.1109/LGRS.2014.2360235 ( 0) 0)
|
| [28] |
Wang R, et al. Joint amplitude-phase compensation for ionospheric scintillation in GEO SAR imaging[J].
IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(6): 3454-3465. ( 0) 0)
|
| [29] |
Hu C, Li Y H, Dong X C, et al. Performance analysis of L-band geosynchronous SAR imaging in the presence of ionospheric scintillation[J].
IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 3454-3465. DOI:10.1109/TGRS.2016.2602939 ( 0) 0)
|
| [30] |
Li Y H, Hu C, Dong X C, et al. Impacts of ionospheric scintillation on geosynchronous SAR focusing: Preliminary experiments and analysis[J].
Science China Information Sciences, 2015, 58(10): 1-3. ( 0) 0)
|
| [31] |
Hu C, Li Y H, Dong X C, et al. Impacts of temporal-spatial variant background ionosphere on repeat-track GEO D-InSAR system[J].
Remote Sensing, 2016, 8(11): 916 DOI:10.3390/rs8110916 ( 0) 0)
|
| [32] |
Kou L L, Wang X Q, Xiang M S, et al. Effect of orbital errors on the geosynchronous circular synthetic aperture radar imaging and interferometric processing[J].
Journal of Zhejiang University Science C, 2011, 12(5): 404-416. DOI:10.1631/jzus.C1000170 ( 0) 0)
|
| [33] |
Kou L L, Xiang M S, Wang X Q, et al. Tropospheric effects on L-band geosynchronous circular SAR imaging[J].
IET Radar, Sonar & Navigation, 2013, 7(6): 693-701. ( 0) 0)
|
| [34] |
Ji Y F, Zhang Q L, Zhang Y S, et al. L-band geosynchronous SAR imaging degradations imposed by ionospheric irregularities[J].
Science China Information Sciences, 2017, 60(6): 060308 DOI:10.1007/s11432-016-9064-1 ( 0) 0)
|
| [35] |
Li D X, Rodriguez-Cassola M, Prats-Iraola P, et al. Modelling of tropospheric delays in geosynchronous synthetic aperture radar[J].
Science China Information Sciences, 2017, 60(6): 060307 DOI:10.1007/s11432-016-9065-1 ( 0) 0)
|
| [36] |
Tofsted D H. Turbulence simulation: Outer scale effects on the refractive index spectrum[R]. Technical Report ARL-TR-548. US Army Research Lab. NM, 2000
( 0) 0)
|
| [37] |
Von Kármán T. Progress in the statistical theory of turbulence[J].
Proceedings of the National Academy of Sciences of the United States of America, 1948, 34(11): 530-539. DOI:10.1073/pnas.34.11.530 ( 0) 0)
|
| [38] |
Tunick A D. The Refractive Index Structure Parameter/Atmospheric Optical Turbulence Model: CN2[M]. U.S. Adelphi: A.R. Laboratory, 1998
( 0) 0)
|
| [39] |
Liu Z P, Hu C, Zeng T, et al. Improved secondary range compression focusing method in GEO SAR[C]. 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 2011: 1373–1376
( 0) 0)
|
| [40] |
Long T, Hu C, Ding Z, et al.. Geosynchronous SAR: System and Signal Processing[M]. Singapore: Springer, 2018
( 0) 0)
|
| [41] |
Zhang D D, Chen Z Y, Dong X C, et al.. Simulating the impacts of ionospheric scintillation on geosynchronous SAR[C]. Proceedings of the 18th International Radar Symposium (IRS), Prague, Czech Republic, 2017
( 0) 0)
|




