② (微波成像技术国家级重点实验室 北京 100190)
③ (中国科学院大学 北京 100049)
④ (南京信息工程大学电子与信息工程学院 南京 210044)
② (National Key Laboratory of Science and Technology on Microwave Imaging, Beijing 100190, China)
③ (University of Chinese Academy of Sciences, Beijing 100049, China)
④ (College of Electronic and Information Engineering, Nanjing University of Information Science & Technology, Nanjing 210044, China)
雷达和通信一体化是近年来研究热点,通过在同一平台上实现雷达和通信多功能并存,可以减小电子系统的体积与能耗,提高资源利用率,减轻多功能间电磁干扰[1–6]。合成孔径雷达(Synthetic Aperture Radar, SAR)是一种高分辨成像雷达,具有全天时、全天候工作的特点,在环境保护、灾害监测、海洋观测、地质测绘等方面有广泛的应用[7–9]。SAR与通信一体化将提升SAR信息交互能力,使成像信息可以及时传输,以便于高效地处理信息,具有更灵活的工作模式。一体化波形设计是实现一体化系统的关键,常见的一体化波形可分为发射统一信号的共享波形[3]和在接收端正交分离的正交波形[2,6]两类。基于共享波形的一体化系统可高效利用系统频率、能量等资源,因其一体化程度最高而备受关注[1,3]。其中,正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)信号[10]是一种被广泛研究的一体化波形,因其具备频谱效率高、可有效对抗多径效应、子载波调制方式灵活、易于实现等优点和宽带可合成的特性,而被应用于雷达系统[11]和雷达通信一体化系统中[4]。然而,OFDM波形存在一些难以避免的缺点[6],一方面,OFDM波形为了防止多径干扰而设置的循环前缀(Cyclic Prefix, CP)会造成SAR图像中的虚假目标,同时降低了信号的使用效率。另一方面,OFDM的子载波频域旁瓣较高[12,13],子载波间干扰严重,这导致其对正交性要求严格,对频率偏移十分敏感。在SAR与通信一体化体制下,一体化平台通过高速移动形成方位向合成孔径,这将不可避免地引入多普勒偏移从而破坏OFDM波形的正交性,使得通信系统的误码率急剧上升,成像性能也受到影响。同时,SAR成像场景复杂,一体化系统具有丰富的多径效应,为确保OFDM具备足够的多径抑制能力,SAR的测绘能力将受到严重限制。
多载波滤波器组(Filter Bank MultiCarrier, FBMC)波形具备类似于OFDM的宽带、窄带性能,是未来5G通信的备选波形之一[14]。FBMC通过精心设计的原型滤波器对子载波进行整形[13],使子载波频域旁瓣极低,从而减轻了子载波之间的干扰,放宽了子载波间的同步需求,使得其在SAR与通信一体化信道中有更优秀的表现。同时,FBMC不采用CP对抗符号间干扰(Inter-Symbol Interference, ISI)和载波间干扰(Inter-Carrier Interference, ICI),避免了成像中虚假目标的存在,提高了频谱效率。因此,相对于OFDM波形,FBMC波形各载波之间不需要保证严格正交,具有更高效的频谱利用率,可以弥补OFDM波形的不足,在SAR与通信一体化体制中有更好的成像性能和通信能力。
本文第2节分析了SAR与通信一体化系统模型,从系统几何模型和信号模型两个角度分析了SAR与通信一体化系统对波形性能的要求。第3节提出了FBMC波形作为一体化波形,推导了FBMC波形的模糊函数并与OFDM波形进行了对比,深入分析了多普勒频偏与多径效应在一体化系统中对FBMC波形的影响,并针对强的多普勒频偏情况提出了补偿算法。第4节通过仿真试验验证了该算法的有效性。
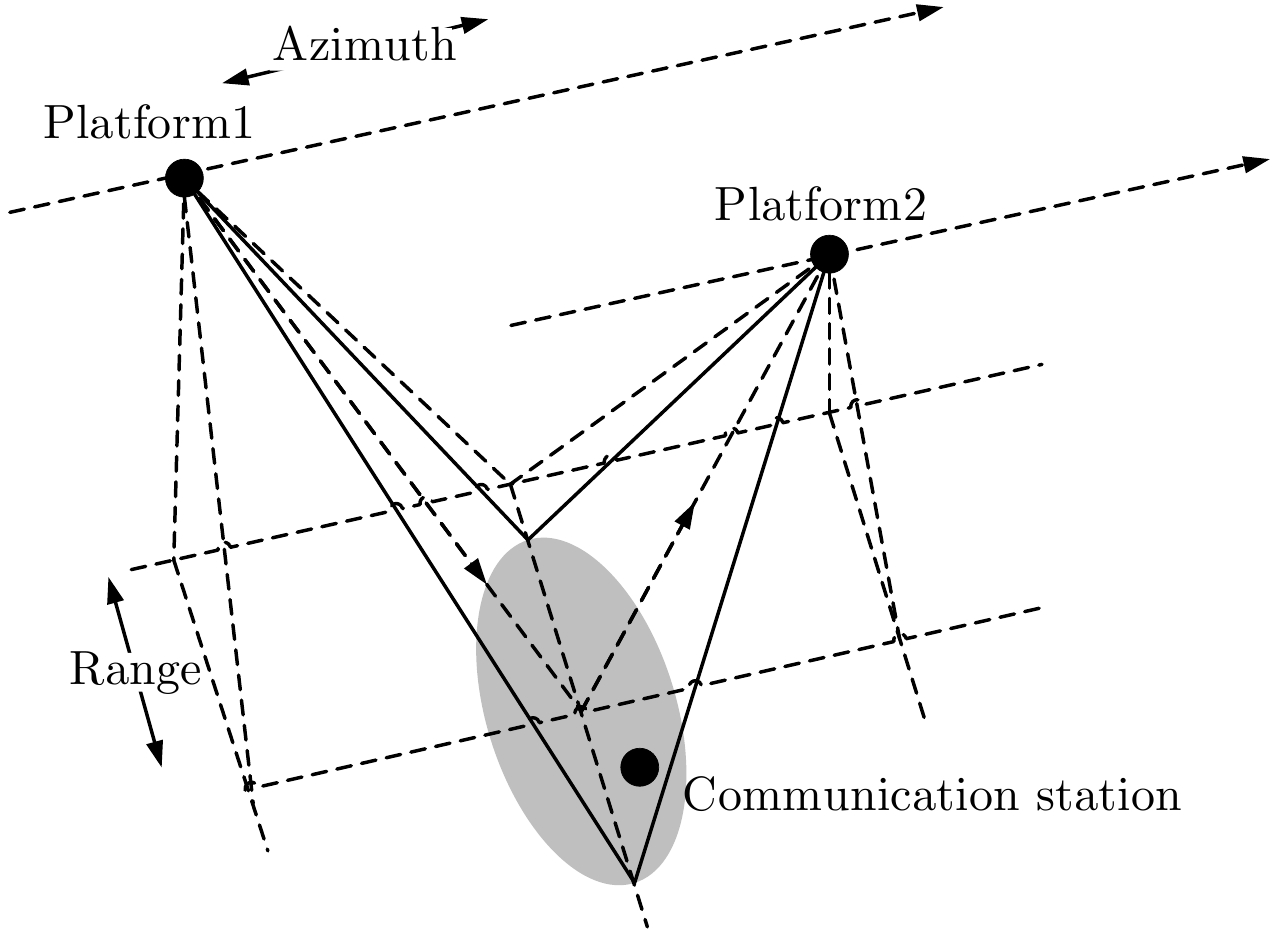
2 SAR与通信一体化系统模型图1为SAR与通信一体化系统的几何模型。一体化平台在飞行过程中向地面发射兼具SAR与通信功能的一体化信号,地面通信站可解调接收通信信息,其他空中飞行平台可通过地面目标的反射回波进行通信信息接收以及SAR模式成像。同时,地面通信站也可向飞行平台发射相同调制的一体化波形进行通信。
|
图 1 SAR与通信一体化系统的几何模型 Fig.1 Geometric model of SAR and communication integration system |
一体化系统通过发射平台与目标的相对移动,在方位向形成大孔径,实现高分辨成像,因而回波中也包含了平台运动信息。由于不同平台的回波可用类似的信道模型描述,在此本文只针对不同飞行平台间的信号模型进行分析。解调至基带的接收信号可以表示为:
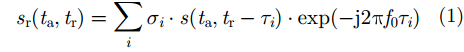
|
其中,
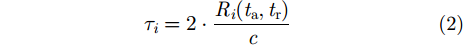
|
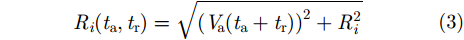
|
其中,
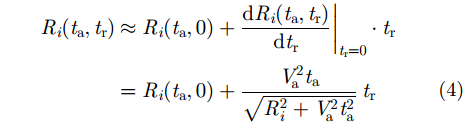
|
令:
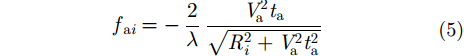
|
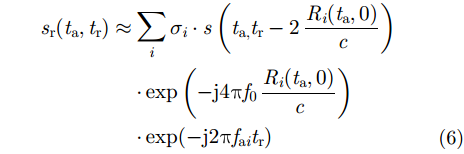
|
由式(6)可见,一体化平台与目标的相对移动将不可避免地引入多普勒偏移到回波信号中,OFDM波形的正交性将会被严重破坏,成像与通信性能将会恶化。同时,来自不同目标的回波造成多径效应,当回波最大时延超过CP长度
FBMC系统通过原型滤波器将信息调制在不同的载频上,可以表示为:
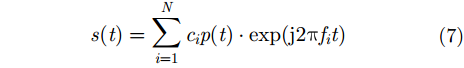
|
其中,N代表子载波个数,
OFDM与FBMC的主要区别在于,前者采用矩形窗作为原型脉冲,其频域子带为Sinc函数,具有较高的旁瓣,而后者采用精心设计的滤波器作为原型脉冲,基本没有带外泄露。文献[13]针对FBMC系统提出的原型滤波器,表示为如下形式:
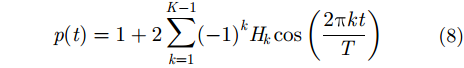
|
其中,K表示重叠因子,
| 表 1 原型滤波器系数 Tab.1 Prototype filter coefficients |
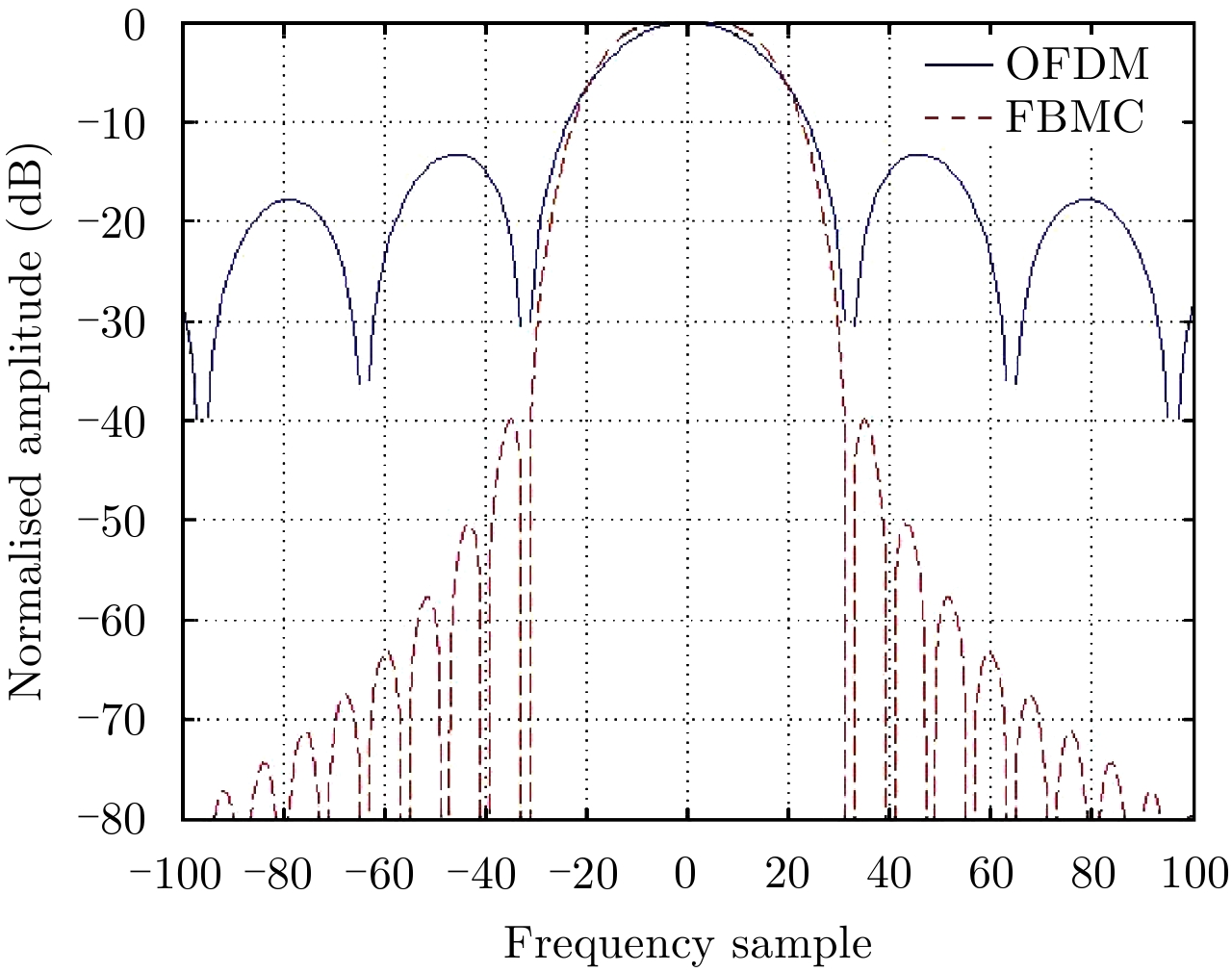
图2为OFDM与FBMC的归一化子载波频域波形对比图,重叠因子K=4。OFDM子载波的副瓣较高,为–13.26 dB,通过PHYDYAS原型滤波器的FBMC子载波副瓣极低,为–39.87 dB,同时,FBMC子载波具有更低的旁瓣,在–100 dB之下,而OFDM的旁瓣约为–40 dB。因此,FBMC可提供更优秀的带外抑制。
|
图 2 OFDM与FBMC子载波频域对比 Fig.2 Subcarrier comparison between OFDM and FBMC |
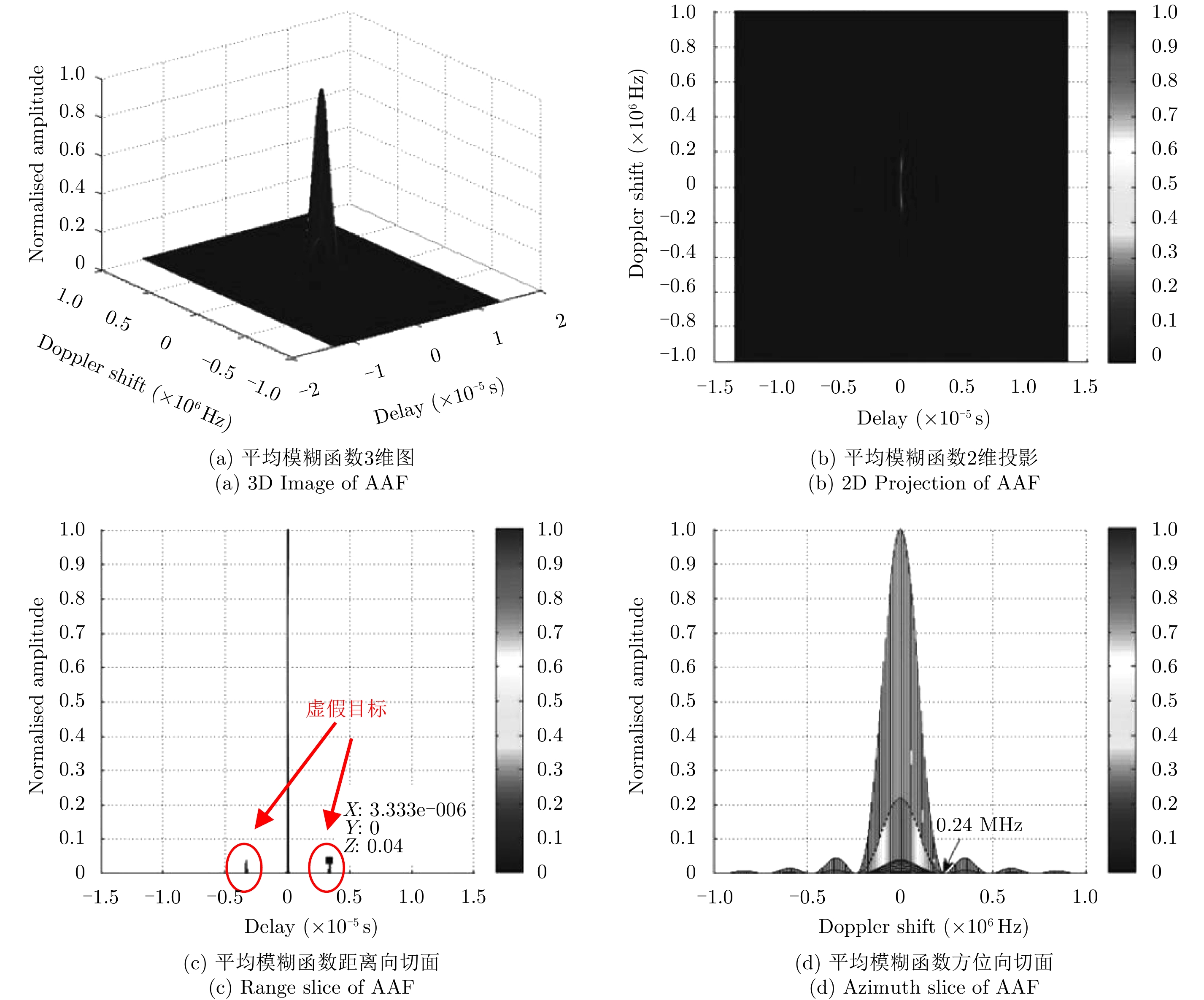
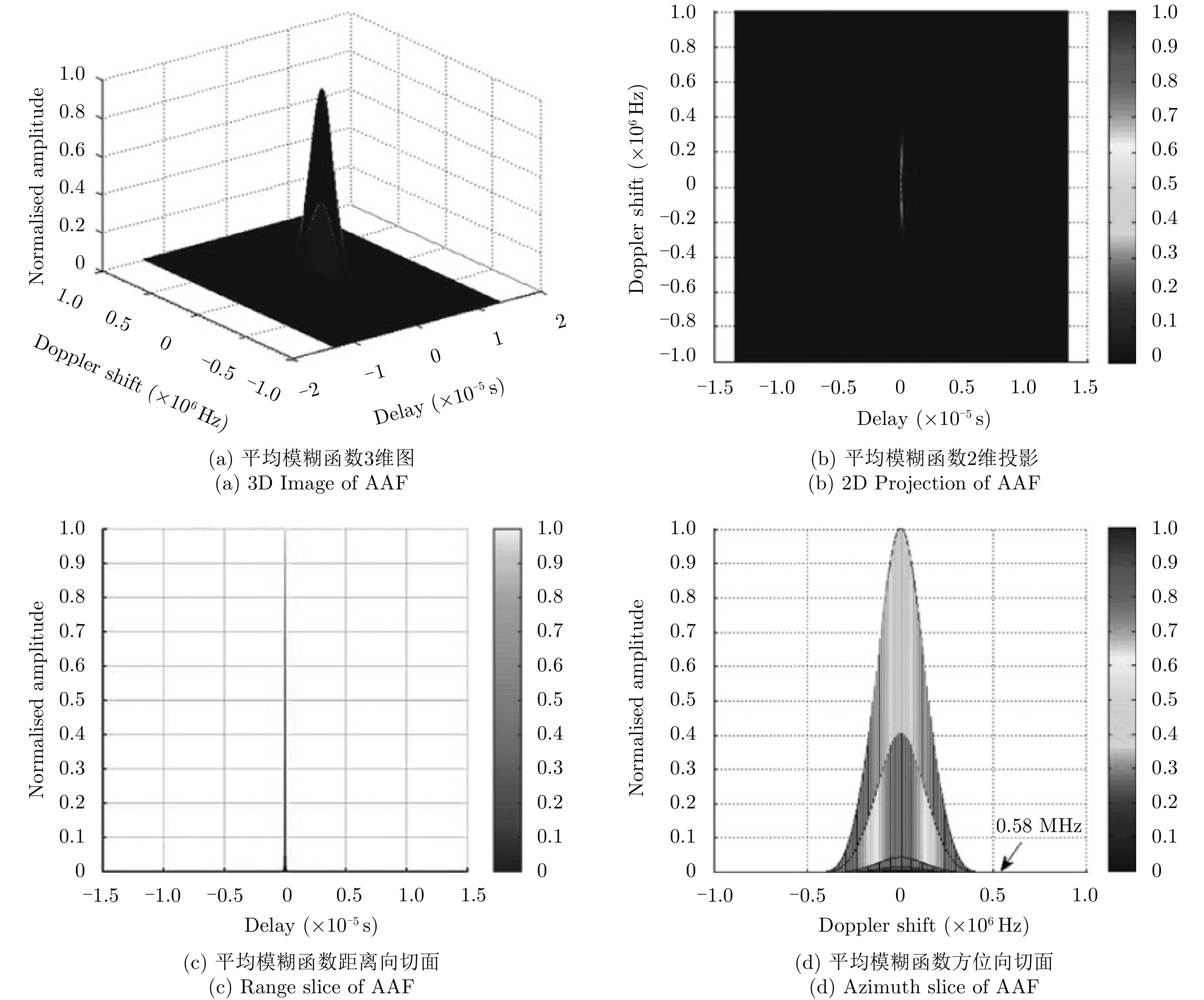
平均模糊函数是关于延时和多普勒频移的函数,能描述波形在距离和多普勒两个维度的分辨力[8]。文献[16]对比了OFDM波形和FBMC波形的平均模糊函数,如图3和图4所示。
|
图 3 OFDM平均模糊函数 Fig.3 OFDM average ambiguity function |
|
图 4 FBMC平均模糊函数 Fig.4 FBMC average ambiguity function |
可以看到,与OFDM类似,FBMC波形的平均模糊函数也呈图钉型,具有良好的成像能力;同时,FBMC波形与OFDM波形具有不同的方位分辨率,这是由于原型脉冲的形式不同,使得FBMC具有更宽的多普勒带宽和更低的带外泄露;OFDM波形与FBMC波形具有相同的距离分辨率,且皆取决于信号带宽,但OFDM波形由于CP的存在,在
由第2节可知,由于SAR场景目标复杂,接收回波具有不同的时延,一体化平台在传输过程中将引入多径效应。OFDM波形通过CP抑制多径效应的影响,需要满足[5]:
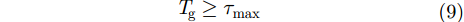
|
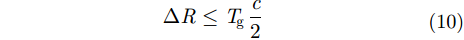
|
一体化系统的测绘带宽受到
|
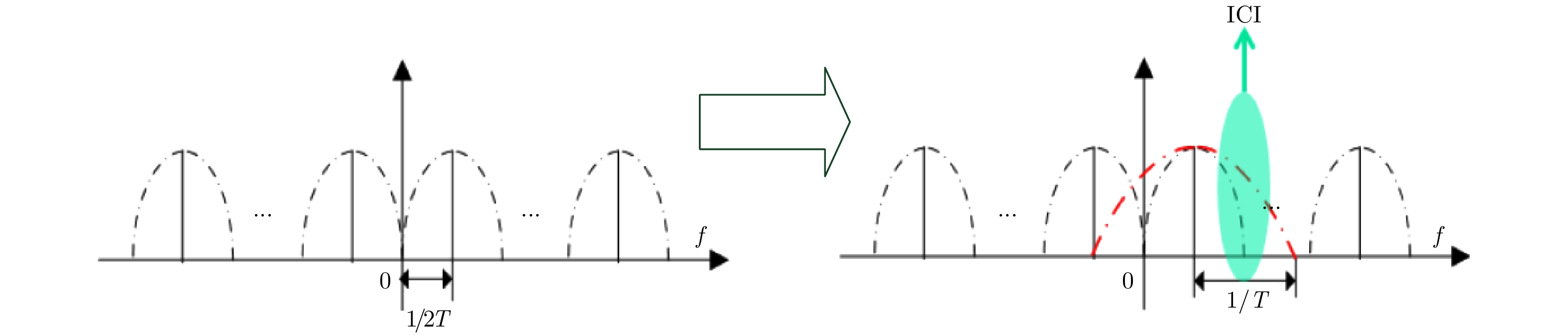
图 5 多径效应对波形正交性的影响示意图 Fig.5 The multipath effect on the orthogonality of waveforms |
当OFDM波形发生频谱泄露时,由于其子载波带外干扰严重,会在展宽时对其余子载波形成严重干扰,从而影响波形正交性。FBMC具有良好的带外抑制,同时利用OQAM编码,可单独地在子载波上进行均衡,并利用接收端的分析滤波器避免子载波间的干扰,实现多径抑制。图6为三径情况下,OFDM与FBMC波形成像和通信性能的仿真结果,OFDM选取
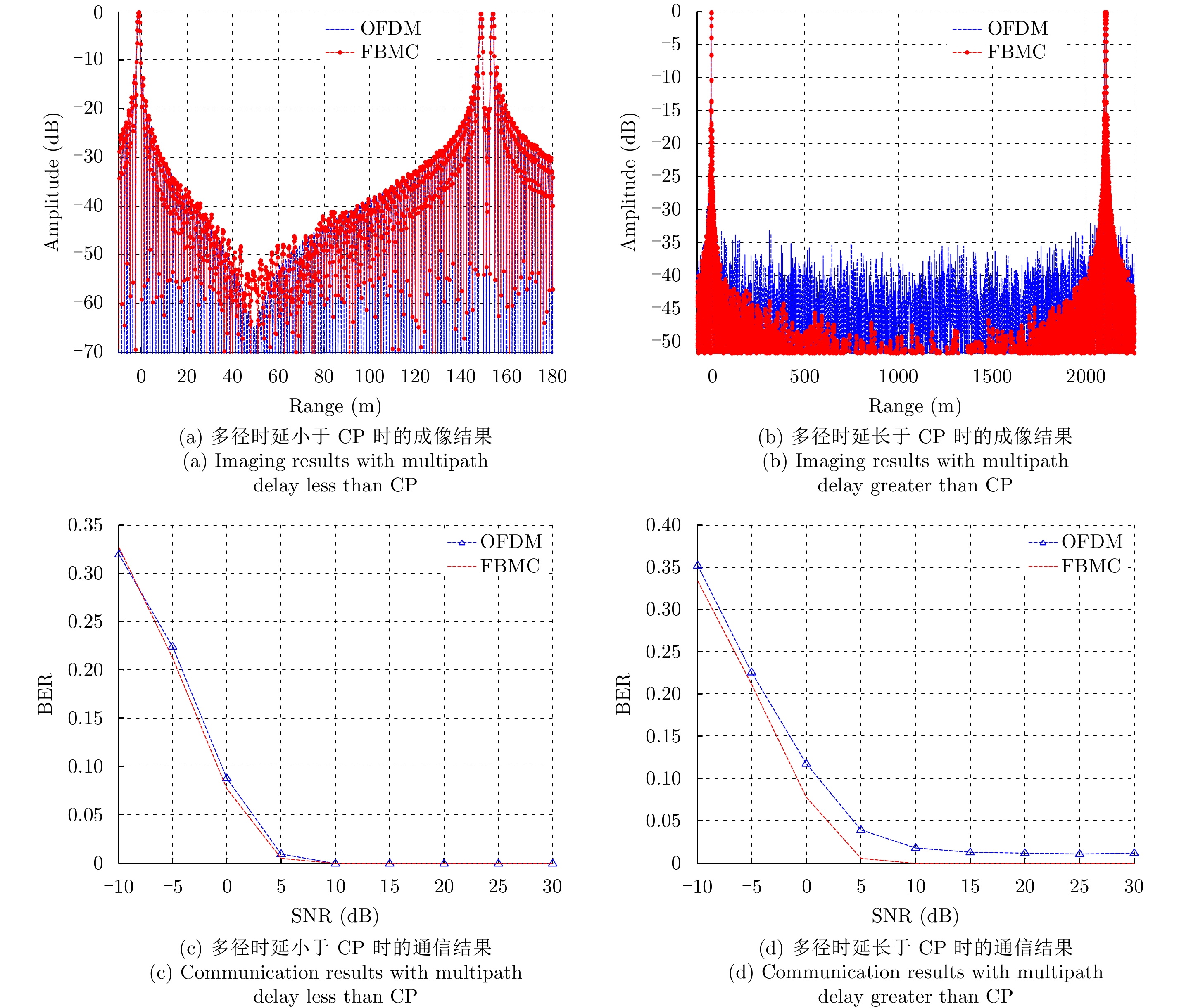
|
图 6 多径时延下的成像与通信性能对比 Fig.6 Comparison of imaging and communication performance under multipath delay |
一体化平台工作过程中将引入多普勒,这将使得一体化波形回波产生一个频偏量,对于正交性要求严格的OFDM波形而言,这种频偏量将使得各载频之间相互干扰,严重影响系统性能。FBMC波形由于子载波之间不存在带外干扰,因而对于多普勒的包容度更大。
当多普勒频移产生时,一体化波形的子带载频会发生偏离,在进行通信解调的过程中,针对相应频点抽取对应编码信息时,可得到:
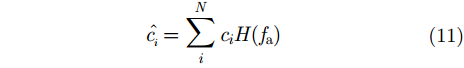
|
此时将无法获取原有的子带权值信息,获取的是来自所有子带信号的干扰叠加值,这将使得通信误码率急剧上升。其原理如图7所示。

|
图 7 多普勒频偏影响OFDM波形正交性的示意图 Fig.7 The Doppler effects on the orthogonality of waveforms |
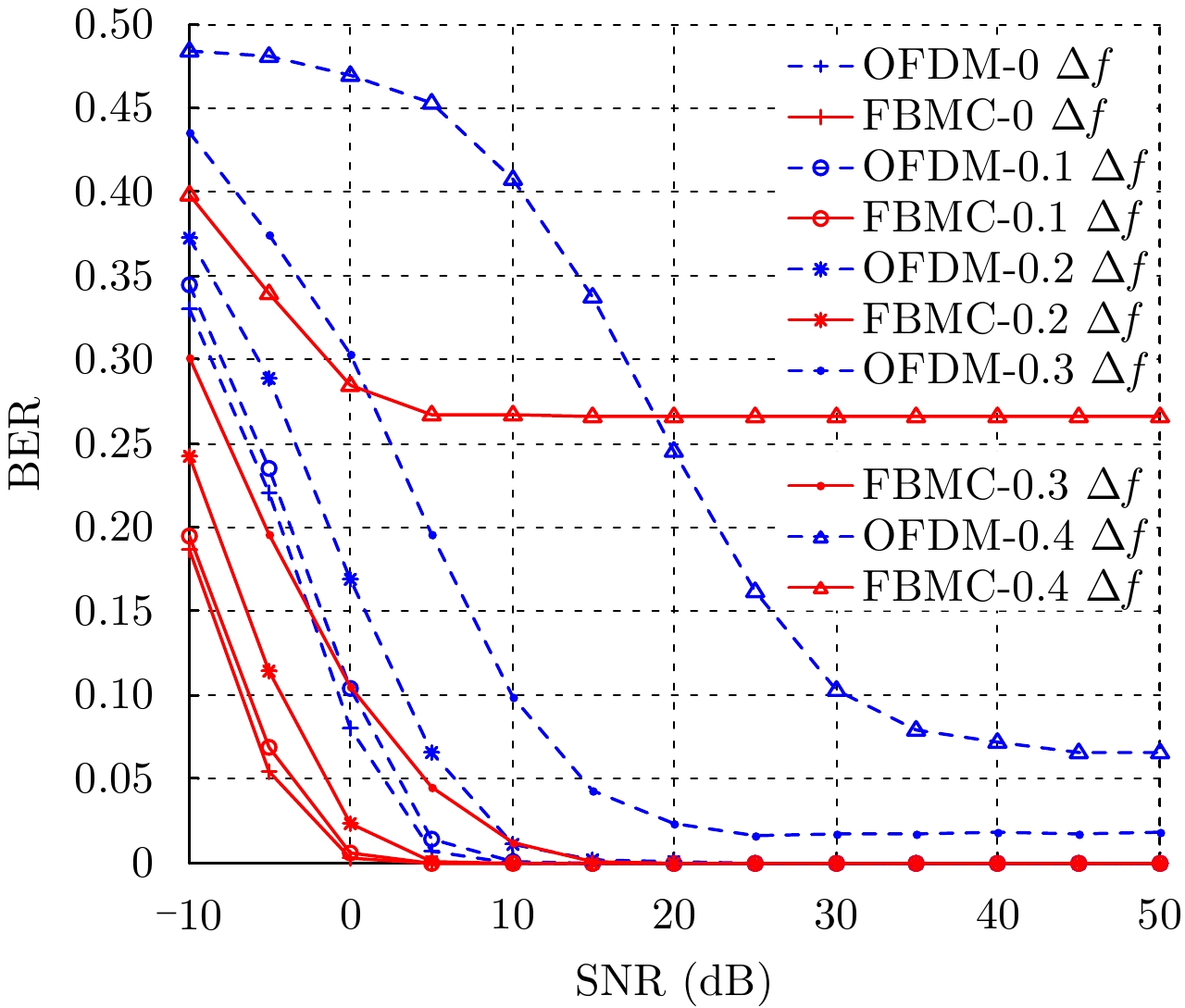
解调结果的失真情况,将取决于原型滤波器的结构,OFDM的带外泄露严重,将使得多普勒频偏下的估计值严重失真,而FBMC的带外泄露极低,可增强波形对多普勒的包容度。图8展示了OFDM和FBMC波形在不同归一化多普勒频偏下的误码率随信噪比变化的情况,此时信号时宽为40 μs,信号带宽为120 MHz,采样频率为200 MHz,信号载频为5.4 GHz。可以看到,OFDM与FBMC的误码率将随着频偏量的增加而恶化。当频偏量小于0.3
|
图 8 归一化频偏下的误码率曲线 Fig.8 Bit error rate under normalized frequency shift |
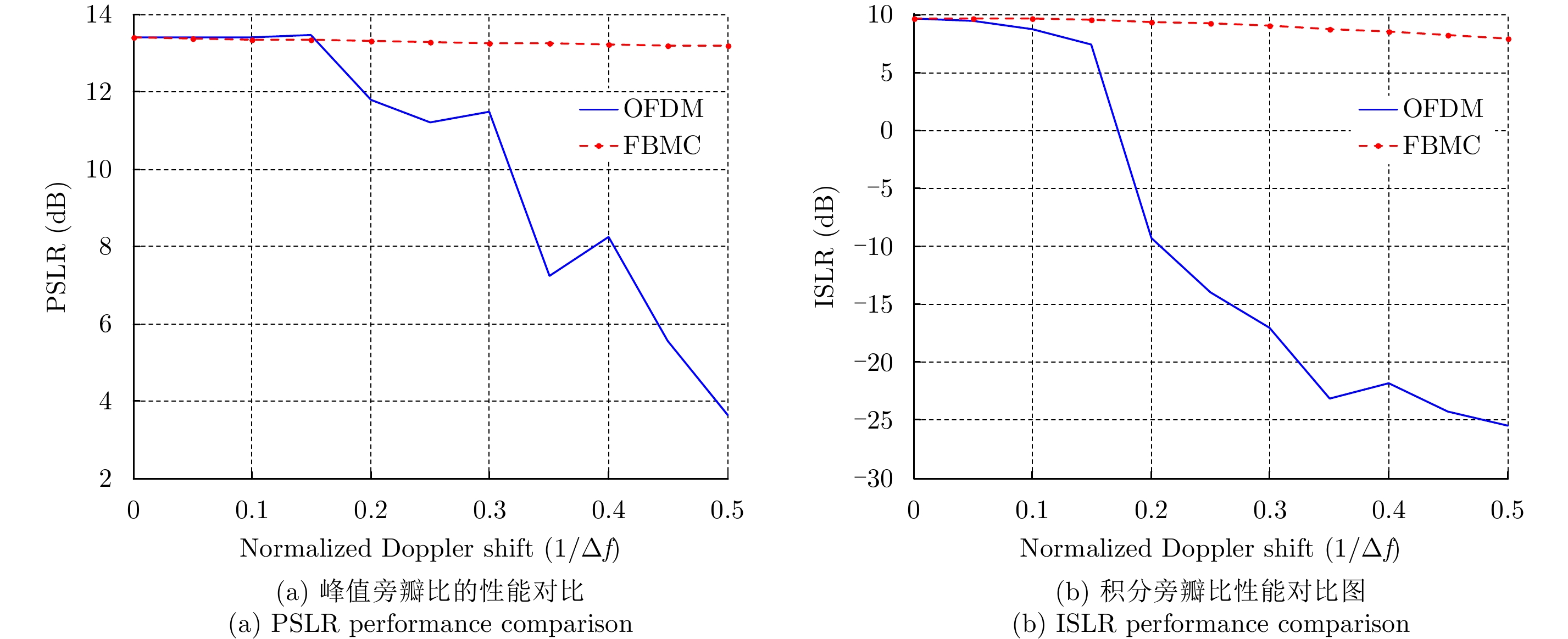
|
图 9 多普勒频偏下的成像性能对比图 Fig.9 Imaging performance comparison under doppler shift |
由式(5)可知,多普勒偏移
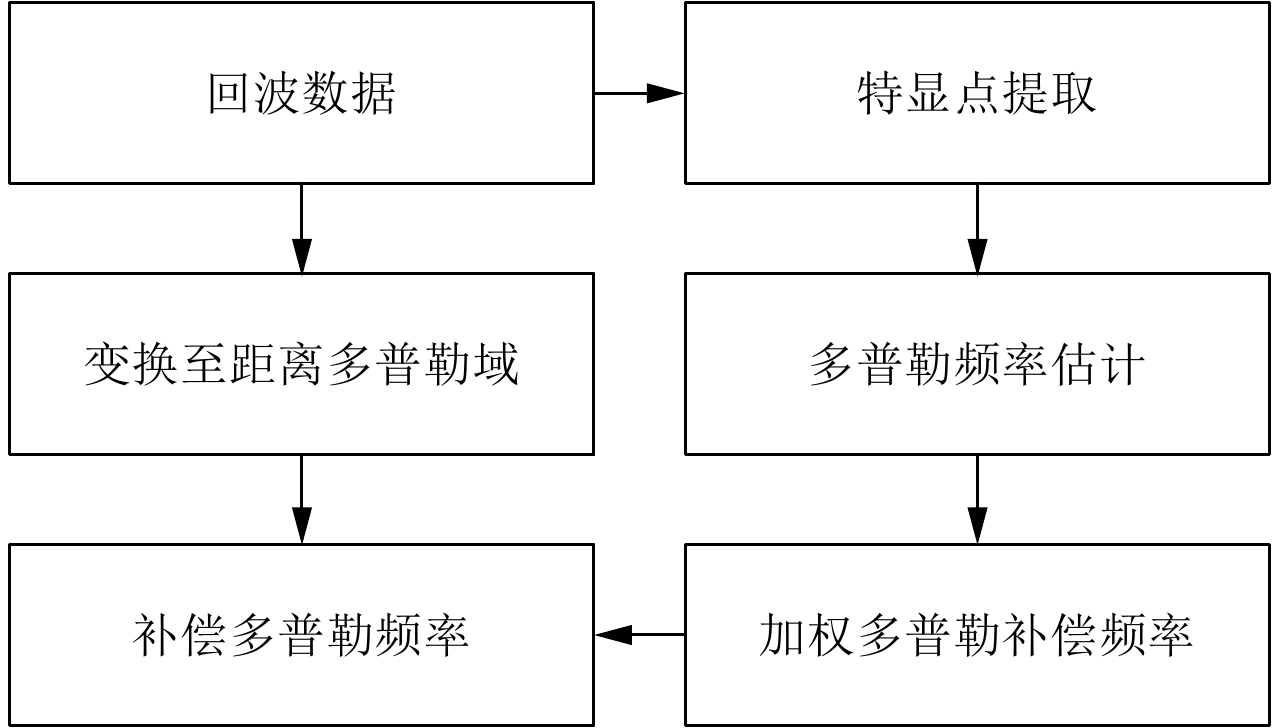
|
图 10 FBMC波形多普勒补偿流程 Fig.10 FBMC waveform doppler compensation process |
步骤1 对回波进行特显点提取,并利用Sign-Doppler Estimator (SDE)估计特显点的多普勒频率;
步骤2 根据特显点强度对多普勒加权求和,得到待补偿的多普勒频率;
步骤3 将回波变换至距离多普勒域;
步骤4 依据估计的平均多普勒频率,补偿回波的多普勒。
通过以上算法,可对FBMC波形回波的多普勒进行有效补偿,从而抑制多普勒频偏的影响。由于不同距离处目标的多普勒频率不同,经过加权多普勒频率补偿后的点目标将存在多普勒残余量,但多普勒残余量的大小将远小于系统的子载频间隔,在FBMC可允许的多普勒频偏范围内,只引起微量的性能损失。所以,FBMC波形的多普勒残余量可以被忽略。经过多普勒补偿后的FBMC波形可利用后续的成像算法和通信解调算法实现高分辨成像和通信功能。
4 仿真分析为了验证基于FBMC波形的SAR与通信一体化波形处理算法的有效性,本文设计了基于图1几何模型的多点目标仿真试验。仿真参数如表2所示,仿真结果如图11、图12所示。
| 表 2 仿真参数 Tab.2 Simulation parameters |
|
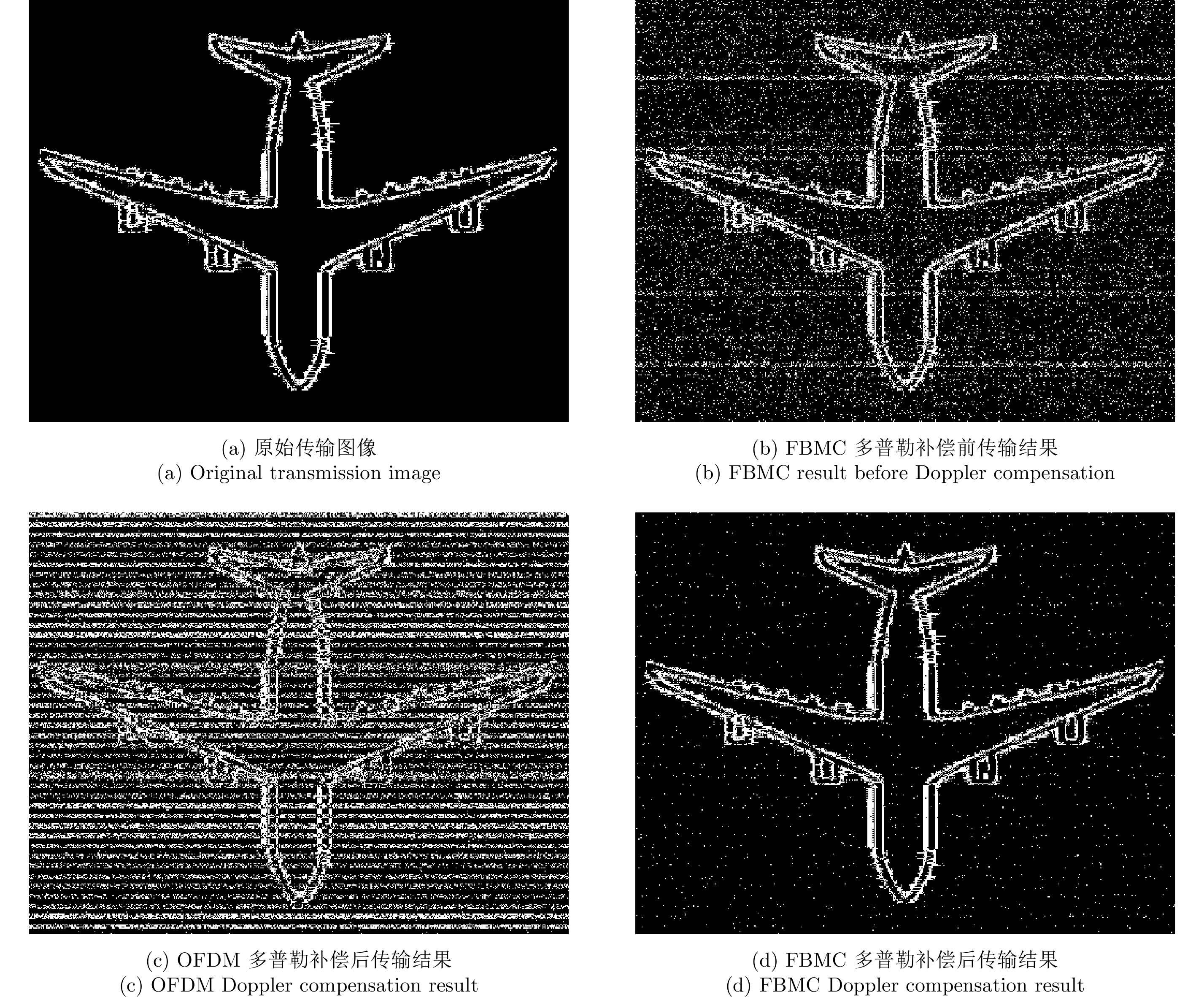
图 11 一体化系统通信性能仿真结果 Fig.11 Integrated system communication performance simulation results |

|
图 12 一体化系统点目标成像性能仿真结果 Fig.12 Integrated system point target imaging performance simulation results |
本实验设计通信信息为图11(a)所示的图片,利用该图片信息构造SAR与通信一体化波形。图11(b)为一体化信道中,未经多普勒补偿的FBMC波形传输结果,由于多普勒频偏的影响,使得FBMC波形的正交性被破坏,无法正确解调通信信息,因此具有较高的误码率,为0.18,图像传输质量较差。图11(c)、图11(d)为经过多普勒补偿后的OFDM与FBMC波形传输结果,由于设置的绘测带宽较大,系统多径时延超过OFDM的CP长度,所以经过多普勒补偿后OFDM波形仍有较高的误码率,为0.12,图像传输质量不理想。经过多普勒补偿后的FBMC波形传输误码率为0.008,其基于子载波调制可以抑制多径效应的影响,图像具有较高的传输质量。
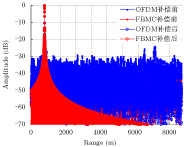
图12为对应情况下的成像结果。图12(a)为未经多普勒补偿的OFDM波形成像结果,图12(b)为未经多普勒补偿的FBMC波形成像结果,图12(c)为经过多普勒补偿的成像结果,三者图像皆出现了不同程度的模糊能量。其中,图12(a)的模糊能量最严重,这是由于多普勒频偏和多径效应的影响,使得OFDM波形正交性被严重破坏,出现了较强的模糊能量。图12(b)和图12(c)的模糊能量具有不同的成因,前者是因为多普勒造成的频偏,后者是由于OFDM波形CP长度不足以对抗多径现象带来的符号间干扰。图12(d)为经过多普勒补偿后的FBMC波形成像结果,模糊能量得到了较好的抑制。图13为成像点目标的距离向切片分析,可以清楚看到,由于多普勒频偏和多径效应导致的载波间干扰,多普勒补偿前后的OFDM信号、多普勒补偿前的FBMC信号都出现了较为明显的模糊能量,使得成像质量下降,经过多普勒补偿后的FBMC信号模糊能量水平较低。表3给出了对应的PSLR和ISLR分析结果,虽然PSLR没有明显变化,但ISLR得到了明显提升。补偿前的OFDM信号ISLR最低,为2.5498 dB,补偿后的FBMC信号ISLR为9.6827 dB,模糊能量得到明显抑制,成像质量得到提升。图14为针对面目标的成像仿真结果,仿真参数与表2一致。可以看到,OFDM多普勒补偿前的图像模糊能量最为严重,FBMC多普勒补偿后的模糊能量得到了较好地抑制,结果与点目标仿真一致。因此,通过本文提出的算法补偿多普勒频率后,一体化平台中的模糊能量可以得到有效抑制,FBMC可以避免载波间干扰,从而获得良好的成像结果。
|
图 13 点目标距离向切片分析 Fig.13 Point target range slice analysis |
| 表 3 点目标成像质量分析 Tab.3 Point target imaging quality analysis |

|
图 14 一体化系统面目标成像性能仿真结果 Fig.14 Integrated system surface target imaging performance simulation results |
本文针对SAR与通信一体化波形技术开展了研究,分析了一体化波形所面临的问题,提出了基于FBMC波形的一体化波形处理算法,并利用仿真实验进行了验证。SAR与通信一体化系统由于平台与目标的相对运动以及复杂的目标场景,将在回波中引入多普勒频偏和丰富的多径效应,这将使得常规的OFDM波形子载波正交性被破坏,无法完成成像与通信任务。本文提出将FBMC波形应用于SAR与通信一体化系统,可以解决OFDM波形面临的问题。首先,FBMC波形不采用CP,在成像时不会产生由CP带来的虚假目标,同时提升了资源利用率,其次,FBMC波形通过OQAM在子载波上的调制,可利用子载波上的均衡抑制多径效应,避免了由CP带来的测绘带宽限制,在宽测绘带系统中有更好的应用,除此之外,FBMC波形对多普勒的包容度更强,在发生少量多普勒偏移时,FBMC具有比OFDM更好的性能。针对多普勒频偏过大的情况,本文提出了基于特显点的距离多普勒补偿算法,可抑制FBMC波形的模糊能量。基于FBMC波形的一体化波形处理算法在宽测绘带SAR与通信一体化系统中有更优秀的性能,SAR与通信一体化仿真实验验证了该结论。
| [1] |
Sturm C and Wiesbeck W. Waveform design and signal processing aspects for fusion of wireless communications and radar sensing[J].
Proceedings of the IEEE, 2011, 99(7): 1236-1259. DOI:10.1109/JPROC.2011.2131110 ( 0) 0)
|
| [2] |
Chiriyath A R, Paul B, and Bliss D W. Radar-communications convergence: Coexistence, cooperation, and co-design[J].
IEEE Transactions on Cognitive Communications and Networking, 2017, 3(1): 1-12. DOI:10.1109/TCCN.2017.2666266 ( 0) 0)
|
| [3] |
Wang W Q, Zheng Z, and Zhang S S. OFDM chirp waveform diversity for co-designed radar-communication system[C]. Proceedings of the 18th International Radar Symposium, Prague, Czech Republic, 2017: 1–9. DOI: 10.23919/IRS.2017.8008139.
( 0) 0)
|
| [4] |
Sit Y L, Reichardt L, Sturm C, et al.. Extension of the OFDM joint radar-communication system for a multipath, multiuser scenario[C]. Proceedings of 2011 IEEE Radar Conference, Kansas City, MO, USA, 2011: 718–723.
( 0) 0)
|
| [5] |
Braun M, Sturm C, Niethammer A, et al.. Parametrization of joint OFDM-based radar and communication systems for vehicular applications[C]. Proceedings of the 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 2009: 3020–3024.
( 0) 0)
|
| [6] |
Han L and Wu K. Multifunctional transceiver for future intelligent transportation systems[J].
IEEE Transactions on Microwave Theory and Techniques, 2011, 59(7): 1879-1892. DOI:10.1109/TMTT.2011.2138156 ( 0) 0)
|
| [7] |
Cumming I G and Wong F H. Synthetic Aperture Radar Imaging[M]. Publishing House of Electronics Industry, 2012.
( 0) 0)
|
| [8] |
林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1984.
Lin Mao-yong and Ke You-an. Radar Signal Theory[M]. Beijing: National Defense Industry Press, 1984. (  0) 0)
|
| [9] |
王杰, 梁兴东, 丁赤飚, 等. OFDM SAR多普勒补偿方法研究[J].
电子与信息学报, 2013, 35(12): 3037-3040. Wang Jie, Liang Xing-dong, Ding Chi-biao, et al. Investigation on the Doppler compensation in OFDM SAR[J]. Journal of Electronics & Information Technology, 2013, 35(12): 3037-3040. DOI:10.3724/SP.1146.2012.01547 (  0) 0)
|
| [10] |
Schulze H and Luders C. Theory and Applications of OFDM and CDMA: Wideband Wireless Communications[M]. New York: Wiley, 2005: 1–10.
( 0) 0)
|
| [11] |
Lellouch G, Mishra A K, and Inggs M. Design of OFDM radar pulses using genetic algorithm based techniques[J].
IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1953-1966. DOI:10.1109/TAES.2016.140671 ( 0) 0)
|
| [12] |
Franken G E A, Nikookar H, and Van Genderen P. Doppler tolerance of OFDM-coded radar signals[C]. Proceedings of 2006 European Radar Conference, Manchester, UK, 2006: 108–111.
( 0) 0)
|
| [13] |
Bellanger M. FBMC physical layer: A primer[C]. P7-ICT Project PHYDYAS, 2010.
( 0) 0)
|
| [14] |
Sexton C, Bodinier Q, Farhang A, et al.. Coexistence of OFDM and FBMC for underlay D2D communication in 5G networks[C]. Proceedings of 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 2016: 1–7. DOI: 10.1109/GLOCOMW.2016.7848863.
( 0) 0)
|
| [15] |
Lee T, Ahn Y, Sim D, et al.. QAM-FBMC system with a robust prototype filter in multipath fading channels[C]. Proceedings of the 18th IEEE International Symposium on Consumer Electronics, JeJu Island, South Korea, 2014: 1–2. DOI: 10.1109/ISCE.2014.6884502.
( 0) 0)
|
| [16] |
Cao W, Zhu J H, Li X T, et al. Feasibility of multi-carrier modulation signals as new illuminators of opportunity for passive radar: Orthogonal frequency division multiplexing versus filter-bank multi-carrier[J].
IET Radar, Sonar & Navigation, 2016, 10(6): 1080-1087. DOI:10.1049/iet-rsn.2015.0414 ( 0) 0)
|
| [17] |
Lim J, Kim S R, and Shin D J. Two-step Doppler estimation based on intercarrier interference mitigation for OFDM radar[J].
IEEE Antennas and Wireless Propagation Letters, 2015, 14: 1726-1729. DOI:10.1109/LAWP.2015.2421054 ( 0) 0)
|




