Image Registration Based on Wave Path Difference Compensation for InISAR
1 引言
雷达成像是雷达信号处理领域一个非常重要的课题,逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)成像可以有效提升雷达的空间检测和目标识别能力[1–3]。ISAR图像是目标沿雷达视线方向和目标运动轨迹方向所成平面的投影,不同观测角度下得到的ISAR图像相差比较大,而且ISAR图像不能完全反映目标真实结构,无法提供目标俯仰向的信息。随着空间监测对于高分辨图像的需求,3维成像技术日趋成为雷达成像领域热点课题[4,5]。
干涉技术首先是在合成孔径雷达(Synthetic Aperture Radar, SAR)成像中被应用的,考虑到ISAR成像为SAR成像的逆过程,自然也就可以将干涉技术引用到ISAR成像领域,发展成为干涉逆合成孔径雷达(Interferometric Inverse Synthetic Aperture Radar, InISAR)3维成像技术[6,7]。InISAR 3维成像系统包含有单天线结构、双天线结构、三天线结构和阵列多天线结构。考虑到单天线和双天线系统结构对于目标运动轨迹的特殊要求以及天线阵列复杂的硬件结构和高昂成本,本文主要研究经典的L型三天线结构。通过使用3部天线,此种3维干涉成像技术可以通过CLEAN算法提取出ISAR图像中的强散射点,并通过同一基线上的两幅ISAR图像的干涉处理得到该散射点的干涉相位[8]。由于干涉相位里面包含有散射点到各雷达天线之间的波程差,经过计算可以得到散射点的3维分布[9]。图像配准是InISAR 3维成像技术里面相当重要的一环,目的是将3幅ISAR图像中的每个散射点对应到相同的像素单元,以确保后续的干涉处理是在相同的散射点之间进行的。
近些年,很多国内外学者发表了ISAR图像配准和InISAR 3维成像相关的算法和应用的论文。InSAR领域基于相关系数的图像配准方法首先被引用到ISAR图像的配准上[10–12],但是SAR和ISAR观测的目标场景有很大的区别,ISAR图像中目标所占的像素单元只是很小的一部分,所以基于相关系数的配准方法并不适用于ISAR图像的配准。文献[13]提出一种基于相位校正的图像配准方法,该方法通过在回波域进行处理,将3部天线的ISAR图像利用各自的参考距离分别完成聚焦,这样在回波就克服了图像失配准的本质原因。该方法对于雷达的测距和测角精度要求比较高,在低信噪比情况下雷达测距和测角精度比较差时,图像配准和3维成像精度较差。在文献[14]中,张群等人提出一种多天线结构3维成像技术,在互相垂直的方向上布置多部天线,利用较长基线对的天线对目标测角,较短的基线对的天线对目标成像,通过长基线测得的目标的较精确的转角对短基线的回波进行补偿,实现ISAR图像的配准,这种成像系统的天线结构相当复杂,给天线布阵带来极大的挑战,并且硬件成本太高。
本文提出一种基于回波域波程差补偿的图像配准方法,使用调频傅里叶变换估计得到目标的旋转角速度,并根据目标旋转角速度构造波程差补偿相位对雷达回波进行相位补偿,最终经过距离维和方位维的距离压缩获得已经配准的ISAR图像。
本文其余部分的结构如下:第2节分析InISAR成像系统的信号模型。本文提出的基于波程差补偿的图像配准方法在第3节进行讨论,在第4节给出实验验证并且与基于相关系数的图像配准方法的性能进行比较。第5节为本文的结论。
2 InISAR成像系统信号模型分析
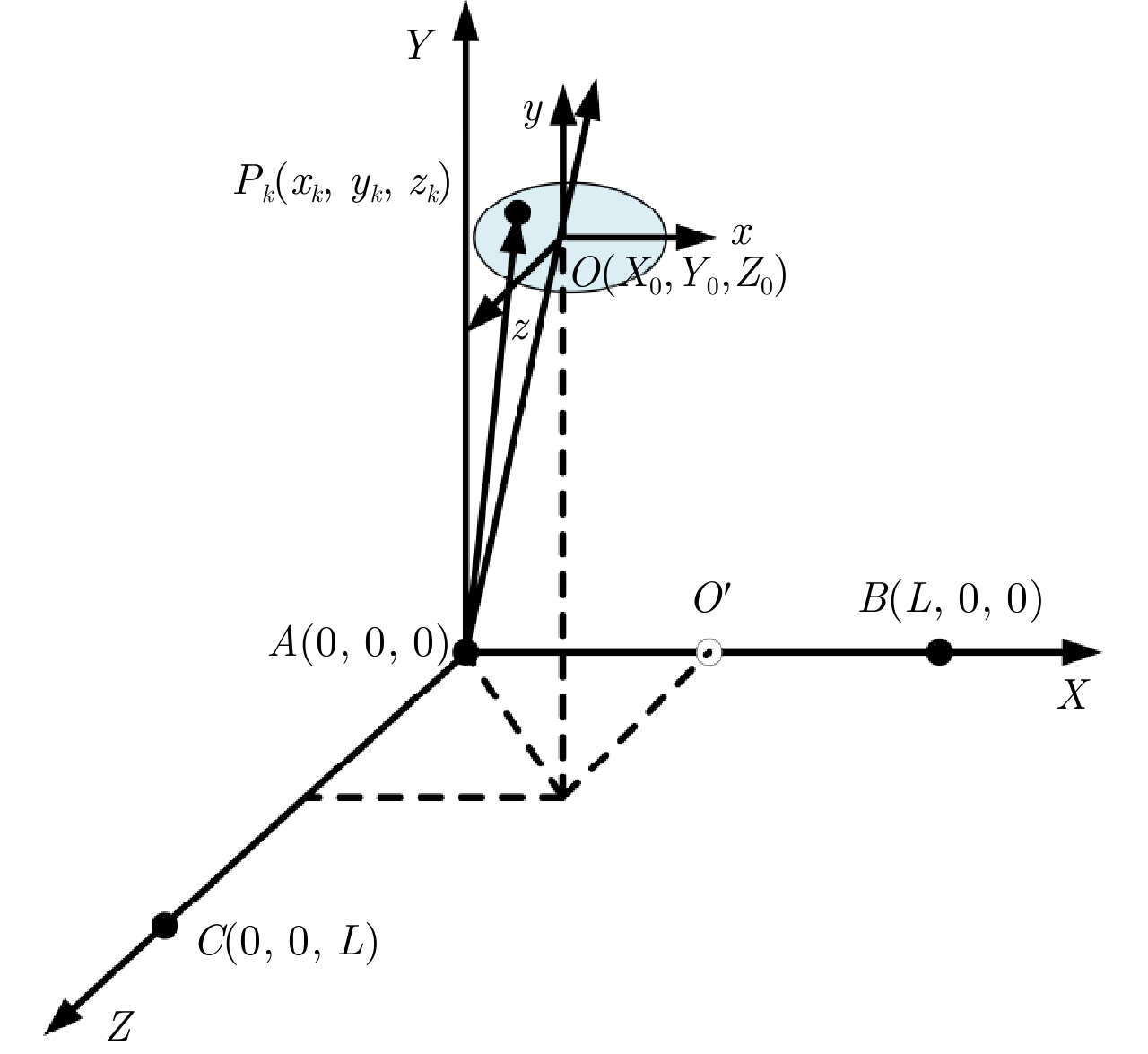
L型三天线构型的干涉3维成像的结构如图1所示,图中包含两个坐标系,即雷达坐标系(A-XYZ)和目标坐标系(O-xyz)。3部天线在雷达坐标系下的位置分别为A(0, 0, 0), B(L, 0, 0), C(0, 0, L),其中L表示成像系统的基线长度,而且基线AB和AC互相垂直。且仅仅A天线为发射天线,A, B和C 3部天线都接收目标回波。
目标坐标系原点为目标的几何中心点O,在雷达坐标系下的坐标为
$O\left( {{X_0},{Y_0},{Z_0}} \right)$
,参考中心点(即目标几何中心点)到3部天线的距离分别为
${R_{OA}}$
,
${R_{OB}}$
,
${R_{OC}}$
。点P为目标上的第k个散射点,在目标坐标系下的坐标为
$\left( {{x_k},{y_k},z{}_k} \right)$
, P点到3部天线的距离分别为
${R_{Ak}}$
,
${R_{Bk}}$
,
${R_{Ck}}$
。此外,目标沿AO, BO和CO方向飞行的速度分别为
${V_{Ak}}$
,
${V_{Bk}}$
和
${V_{Ck}}$
。
$\hat t$
为目标成像快时间,
${t_m}$
为成像慢时间。
此外,设雷达发射线性调频信号,信号载频为
${f\!_{\rm{c}}}$
,带宽为BW,脉冲持续时间为
${T_{\rm{p}}}$
,脉冲重复间隔为
${T_{\rm{r}}}$
,成像总时间为
${T_1}$
,第k个散射点的散射强度为
${\sigma _k}$
。发射信号的调频斜率为
$\gamma $
,雷达波长为
$\lambda $
,光速为
$c$
。所有3部雷达均使用A天线测得的参考距离
${R_{{\rm{ref}}A}}{\rm{ = }}{R_{AO}}$
进行解线频调处理。设
$ {R_{\Delta Ak}} =$
$ {R_{Ak}} - {R_{{\rm{ref}}A}}$
,
${R_{\Delta Bk}} = {R_{Bk}} - {R_{{\rm{ref}}A}}$
,
${R_{\Delta Ck}} = {R_{Ck}}$
$ - {R_{{\rm{ref}}A}}$
,然后雷达A, B和C经过解线频调处理之后的回波为:
干涉逆合成孔径雷达成像技术是高分辨2维ISAR成像和干涉技术的结合,因此,高分辨的ISAR成像是InISAR 3维成像的前提条件。经过文献研究可知,ISAR 2维成像技术已经比较成熟,根据传统的平动补偿方法和脉冲压缩方法可以得到目标比较清晰的2维ISAR图像。在3部天线都完成2维ISAR成像之后,需要通过图像配准方法将同一散射点在3幅不同ISAR图像当中对齐到同一像素单元,以确保后续的干涉处理过程是对相同散射点进行干涉处理,以解算出各散射点的空间位置。根据ISAR成像理论,A, B, C 3部天线所成的ISAR复图像分别为:
根据式(4)和式(5)可知,同一散射点在A, B两幅ISAR图像当中的位置有一定的偏移:
根据式(7)和式(8),代入X波段宽带成像雷达典型系统参数
$\rm{BW} = 1\;GHz$
,
$c = 3 \times {10^8}$
,
$\lambda = 0.03\;{\rm m}$
以及散射点不同时间到雷达距离,可得到此时A, B天线ISAR图像在距离向和方位向偏移的距离单元数:
由式(7)和式(8)可知,ISAR图像距离向的失配主要由成像起始时刻目标(
${t_m} = 0$
)到不同雷达的波程差
$\left(\left( {{R_{\Delta Ak0}} - {R_{\Delta Bk0}}} \right)\left| {_{{t_m} =0}}\right.\right) $
引起,而方位向的失配则是由成像时间内积累的波程差
$\left(\left( {{R_{Ak}} - {R_{Bk}}} \right)\left| {_{{t_m} = {T_1}}}\right.\right.$
$ \left. {- \left( {{R_{Ak}} - {R_{Bk}}} \right)\left| {_{{t_m} = 0}}\right. } \right)$
引起。根据式(9)和式(10)的计算结果可知,ISAR图像在距离向的失配量比较小,但是方位向的失配量已经达到十几个分辨单元。综上所述,当3部天线均采用A天线测得的到目标的距离进行解线频调处理时,ISAR图像之间的失配准现象比较严重。
因此,在回波域将由天线位置不同而引起的波程差补偿掉,就可以实现各天线ISAR图像的配准。在完成图像配准之后,对两幅ISAR图像进行干涉处理,进而解算出目标中各散射点的3维位置关系。
3 基于波程差补偿的ISAR图像配准方法
3.1 基于调频傅里叶变换的波程差估计
从式(9)和式(10)可见,当雷达B和雷达C的回波都用雷达A测得的参考距离
${R_{{\rm{ref}}A}} = {R_{AO}}$
进行解线频调处理并成像时,B图像和A图像以及C图像和A图像之间的失配准现象比较严重。但是,用雷达B和雷达C到目标的距离分别对各自回波进行解线频调处理时,即
${R_{{\rm{ref}}B}} = {R_{BO}}$
,
${R_{{\rm{ref}}C}} = {R_{CO}}$
,图像之间的失配准现象会得到较好的改善。这样可得
$R'\!\!_{\Delta Bk} = {R_{Bk}} - {R_{BO}}$
,
$R'\!\!_{\Delta Ck} = {R_{Ck}} - {R_{CO}}$
。最终,距离向和方位向的偏移量为:
由式(13)和式(14)可知,采用3部雷达各自到目标的距离对各自雷达回波进行解线频调处理并成像,便可以有效减小距离向和方位向的偏移。因此,雷达B和雷达C需要补偿的波程差分别为:
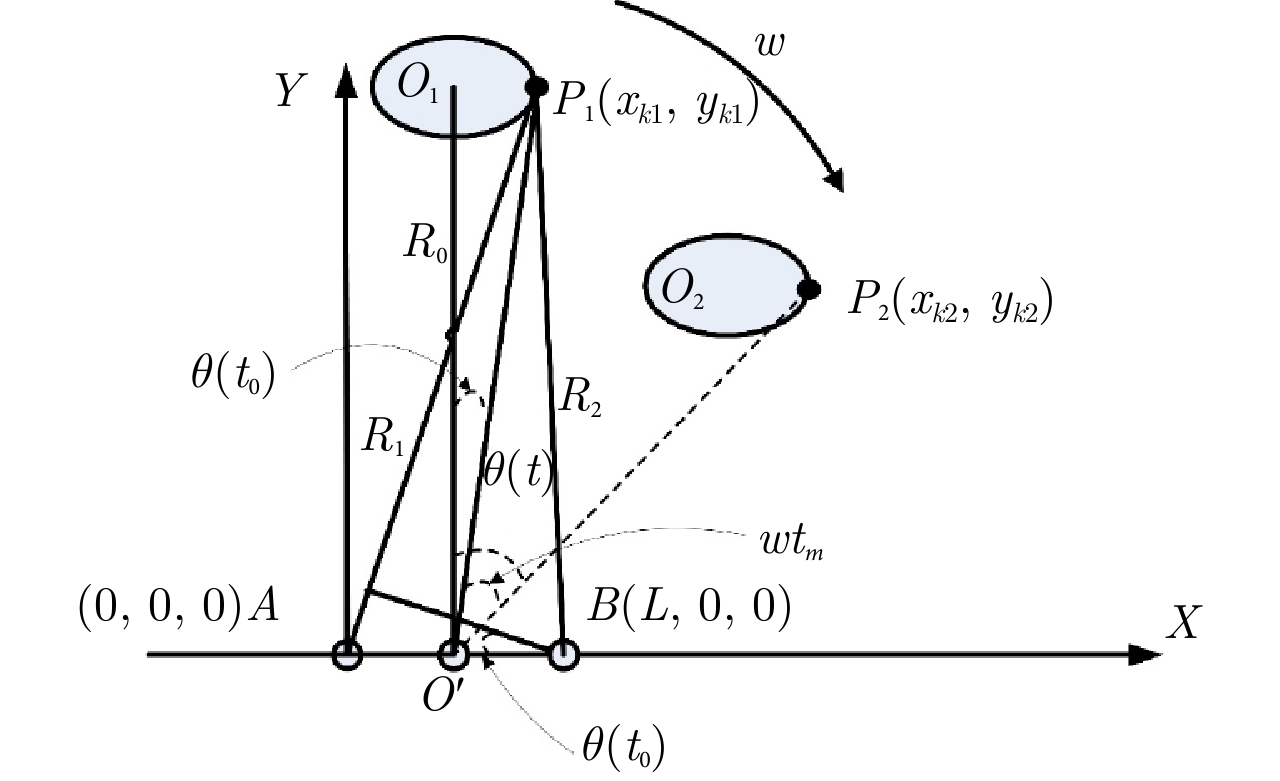
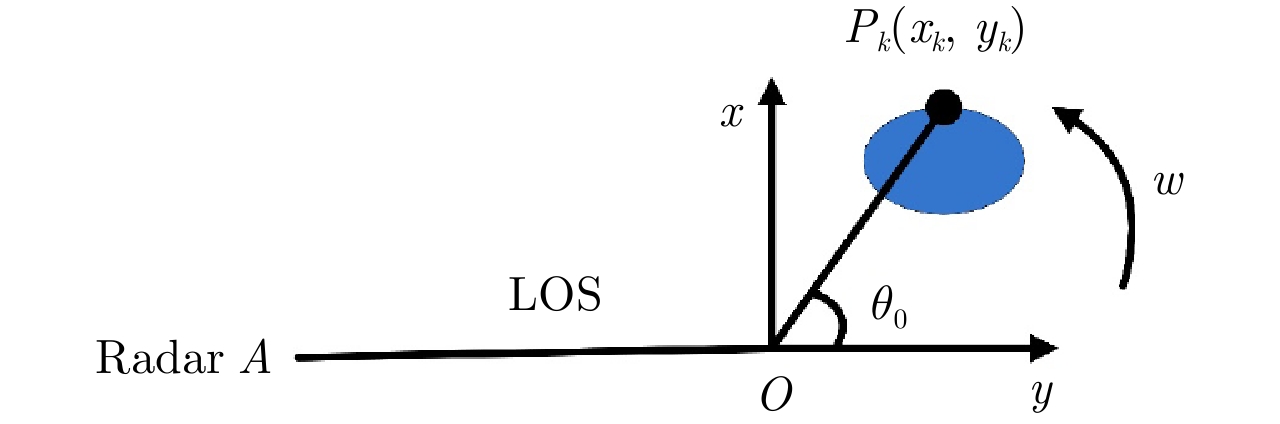
图2描述了远场目标在XOY平面的运动模型,目标在XOY平面以
${w^{AB}}$
做匀速转动。图中
${O_1}$
和
${O_2}$
分别为不同时刻目标的中心位置。
${O'}$
为基线AB的中点,并且直线
${O_1}{O'}$
垂直于X轴。P为目标上任意一散射点,
${O'}$
到散射点P的连接线与直线
${O_1}{O'}$
之间的夹角为
$\theta \left( {{t_m}} \right)$
,此处
${t_m}$
为成像慢时间,
$0 \le {t_m} \le {T_1}$
。散射点P到雷达A和雷达B的距离分别为
${R_1}\left( {{t_m}} \right)$
和
${R_2}\left( {{t_m}} \right)$
,均为慢时间
${t_m}$
的函数。平面YOZ内的运动情况和XOY平面内的运动情况类似,且其转动角速度为
${w^{AC}}$
。
由图2中散射点与雷达位置之间的几何关系,可计算得到散射点P到雷达A和雷达B的距离差为:
同理,参考距离差:
其中,
${R_{A{O_1}}}\left( {{t_m}} \right)$
和
${R_{B{O_1}}}\left( {{t_m}} \right)$
分别为雷达A和雷达B的参考距离。同样,雷达A和雷达C之间的参考距离差为
$\Delta R_m^C \approx L \bullet {w^{AC}}{t_m}$
。
经过上述分析可知,ISAR图像配准问题可由波程差的估计问题转化为目标角度转动参数的估计问题,可以通过自发自收的雷达A对目标的转动角速度进行估计。
经过平动补偿之后,目标可被视为转台目标,具体转台模型如图3所示。对于相对雷达做匀速转动的目标,目标上散射点到雷达距离为:
雷达A的经过剩余视频相位和包络斜置项消除之后的1维距离像为:
其中,
${R_{\Delta Ak}} = {y_k}\cos w{t_m} - {x_k}\sin w{t_m}$
,因此1维距离像的相位项为:
因此,当成像时间内目标转角比较小的情况下,回波多普勒频率为:
由式(22)可见,回波在慢时间域为线性调频信号,且调频率为:
式(23)表明,在给定雷达波长
$\lambda $
和散射点的纵坐标
${y_k}$
之后,目标回波在多普勒域的调频斜率与目标的转动角速度成一一对应关系。换句话说目标旋转角速度的估计问题就转化为回波多普勒域的调频率估计问题。因此,调频傅里叶变换可以作为目标回波慢时间域调频率k估计的有效方法。回波强散射点的1维方位像的调频傅里叶变换的定义式为:
其中,
${S_{AA}}\left( {f,{t_m}} \right)$
表示雷达A回波强散射点所在的单元的1维方位像,且调频傅里叶变换过程中需要补偿的调频斜率的范围为:
在每一个补偿的调频斜率
${\gamma _m}$
下,计算调频傅里叶变换结果
$F\left( {f,\gamma } \right)$
的熵,以熵最小为准则选择最佳补偿的调频斜率为回波多普勒域调频斜率的估计值。设调频傅里叶变换的结果为
$F\left( {m,n} \right)$
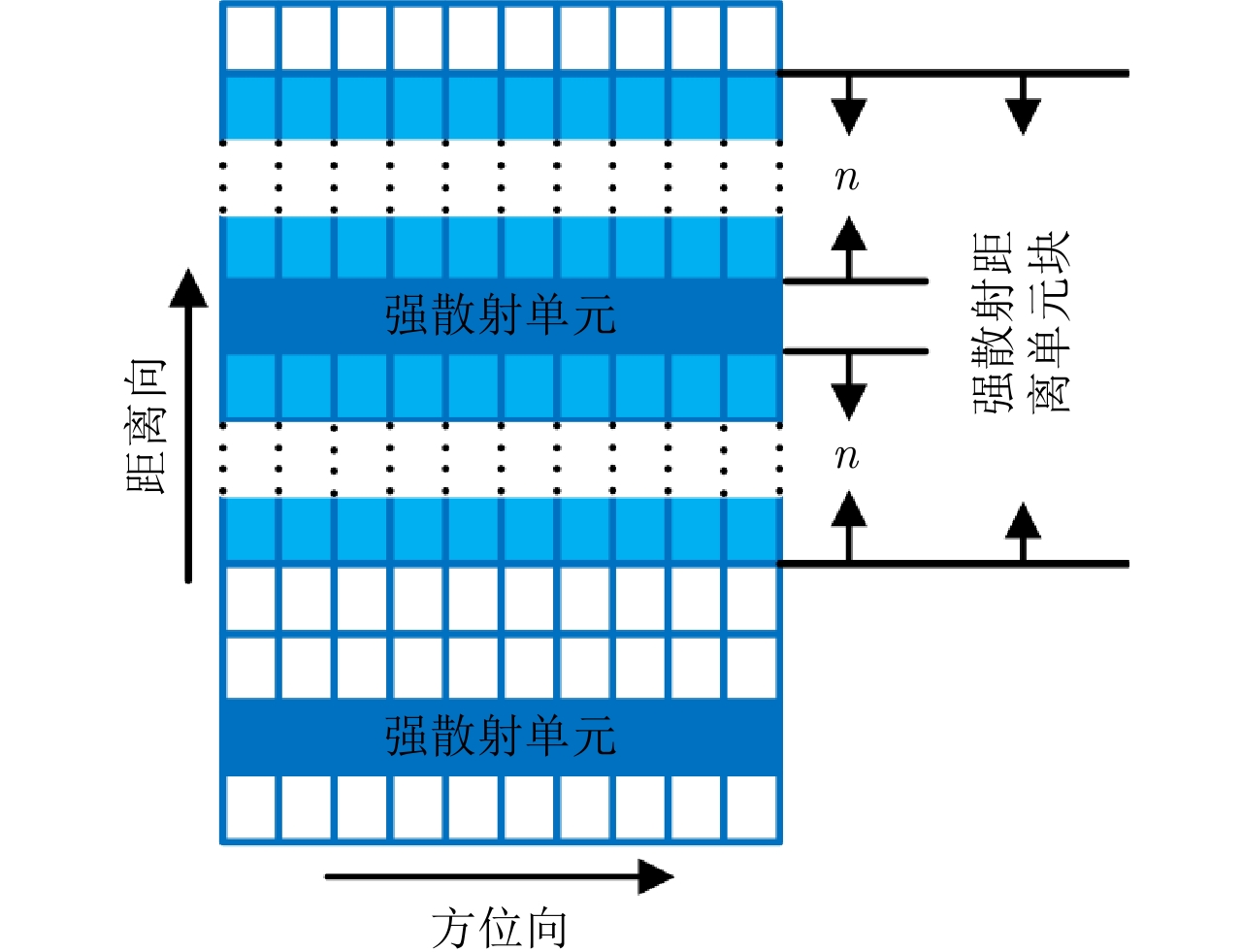
,则熵的计算式如式(26)所示。进一步为了估计结果的稳定性,此处选择强散射点所在距离单元的前后多个距离单元(调频斜率变化不大)的强散射单元块的1维方位像作为整体对目标回波多普勒频率的调频斜率进行估计。具体的强散射单元块的选择方法如图4所示。
其中,强散射单元块由2n+1个1维方位像组成,分别为强散射点单元所在的1维方位像,以及其前后各n个距离单元的1维方位像。具体的强散射单元块的组成如图4中阴影部分所示。此处选择强散射单元块遵循两个原则:(1)充分利用强散射单元的峰值的旁瓣信息;(2)同一个强散射单元块不同时包含两个强散射单元。
在各个强散射单元块估计得到调频斜率之后,再根据调频斜率与散射点距离
${y_k}$
成线性关系的特点,对多个强散射单元块估计得到的调频斜率进行最小二乘拟合,得到的直线的斜率K与转动角速度成唯一对应关系:
3.2 基于波程差相位补偿的ISAR图像配准
进一步根据上述推导得到的需要补偿的波程差,可以构造雷达B和雷达C回波分别需要补偿的相位为:
然后,对雷达B和雷达C经过解线频调处理的接收回波进行相位补偿:
最后,对雷达B和雷达C的经过相位补偿之后回波进行成像处理,最终雷达B和雷达C所成的ISAR图像与雷达A的ISAR图像是完全配准的。因为ISAR图像配准仅仅是InISAR 3维成像的中间步骤,所以在经过上述方法获得已经配准的ISAR图像之后,利用干涉技术来提取目标的干涉相位以及各散射点的坐标信息:
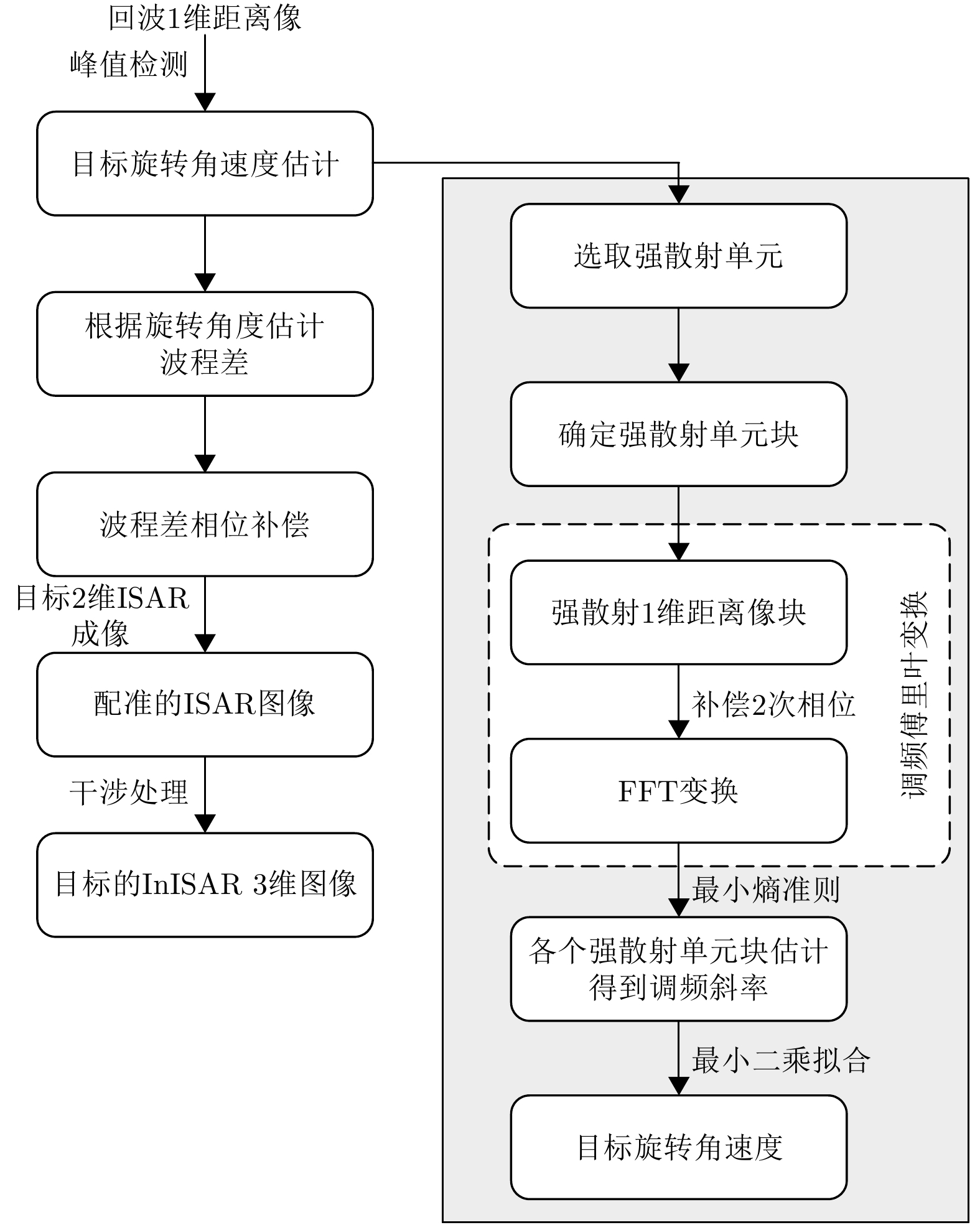
综上所述,整个InISAR 3维成像算法的流程如图5所示。
4 仿真实验
为了验证所提出方法的有效性,本部分就所提出的方法进行仿真实验,并与基于相关系数的ISAR图像配准算法进行比较。InISAR成像系统结构如图1所示,基线长度L=10 m。雷达和目标参数如表1所示。
表 1 (Tab. 1
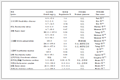
表 1 雷达和目标的参数
Tab. 1 Parameters of experiment
| 雷达参数 |
数值 |
目标参数 |
数值 |
| 信号载频fc |
10 GHz |
散射点数 |
8 |
| 信号带宽BW |
1 GHz |
目标高度 |
100 km |
| 距离分辨率 |
0.15 m |
转动角速度 |
0.0112 rad/s |
| 脉冲时宽Tp |
0.1 ms |
最大尺寸 |
5.7 m |
| 脉冲重复频率PRF |
100 Hz |
|
|
| 脉冲数量 |
500 |
|
|
|
表 1 雷达和目标的参数
Tab.1 Parameters of experiment
|
4.1 基于波程差补偿的图像配准方法实验结果
4.1.1 目标旋转角速度估计结果
目标回波多普勒域调频斜率
${\gamma _{\rm{comp}}}$
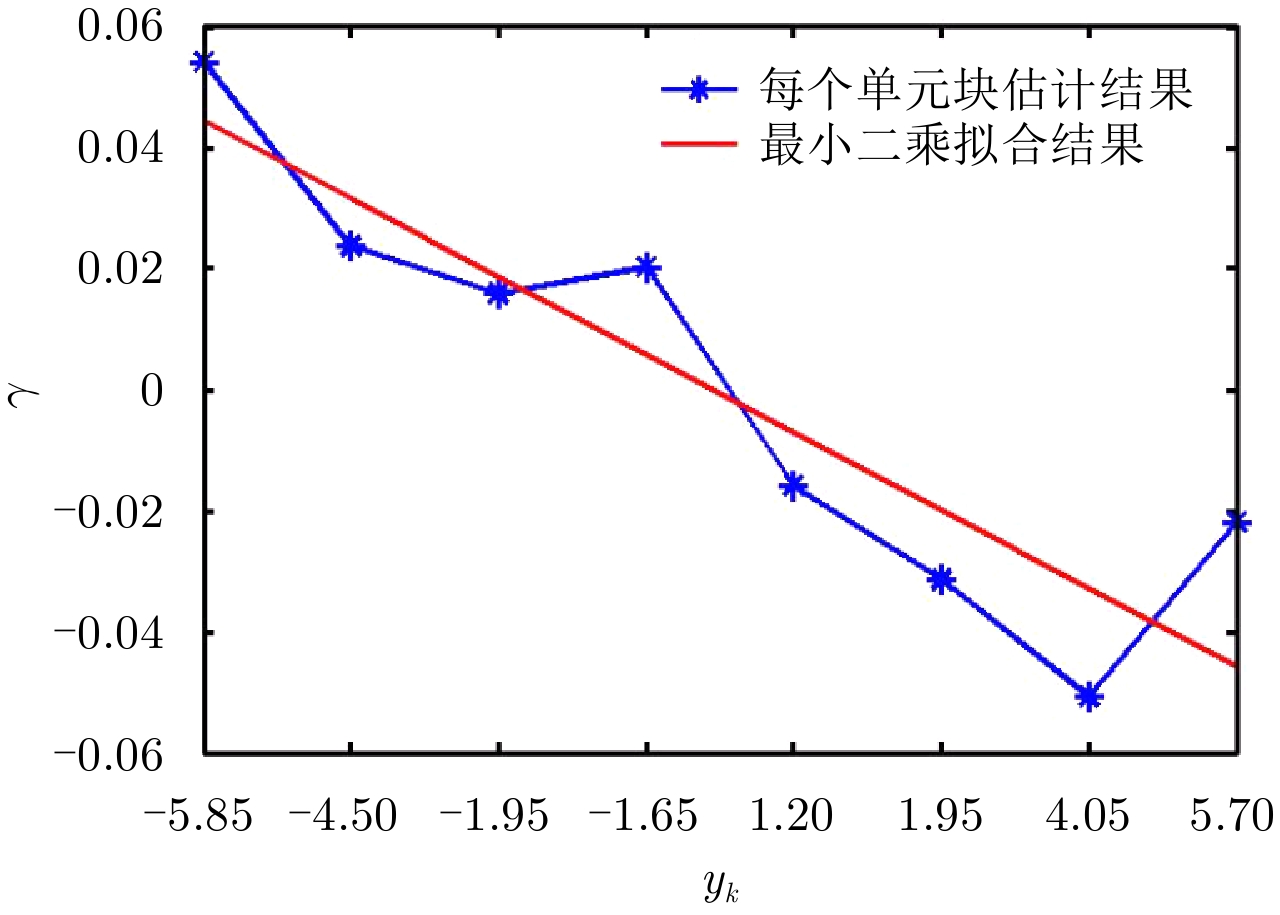
估计结果如图6所示,蓝色线为调频傅里叶变换之后用最小熵法搜索得到的各距离单元块的调频斜率估计结果,红色线为最小二乘拟合的结果。计算红线的斜率即可计算得到目标的旋转角速度:
$w = \sqrt { - \lambda \left| K \right|/2} = 0.{\rm{0108}}$
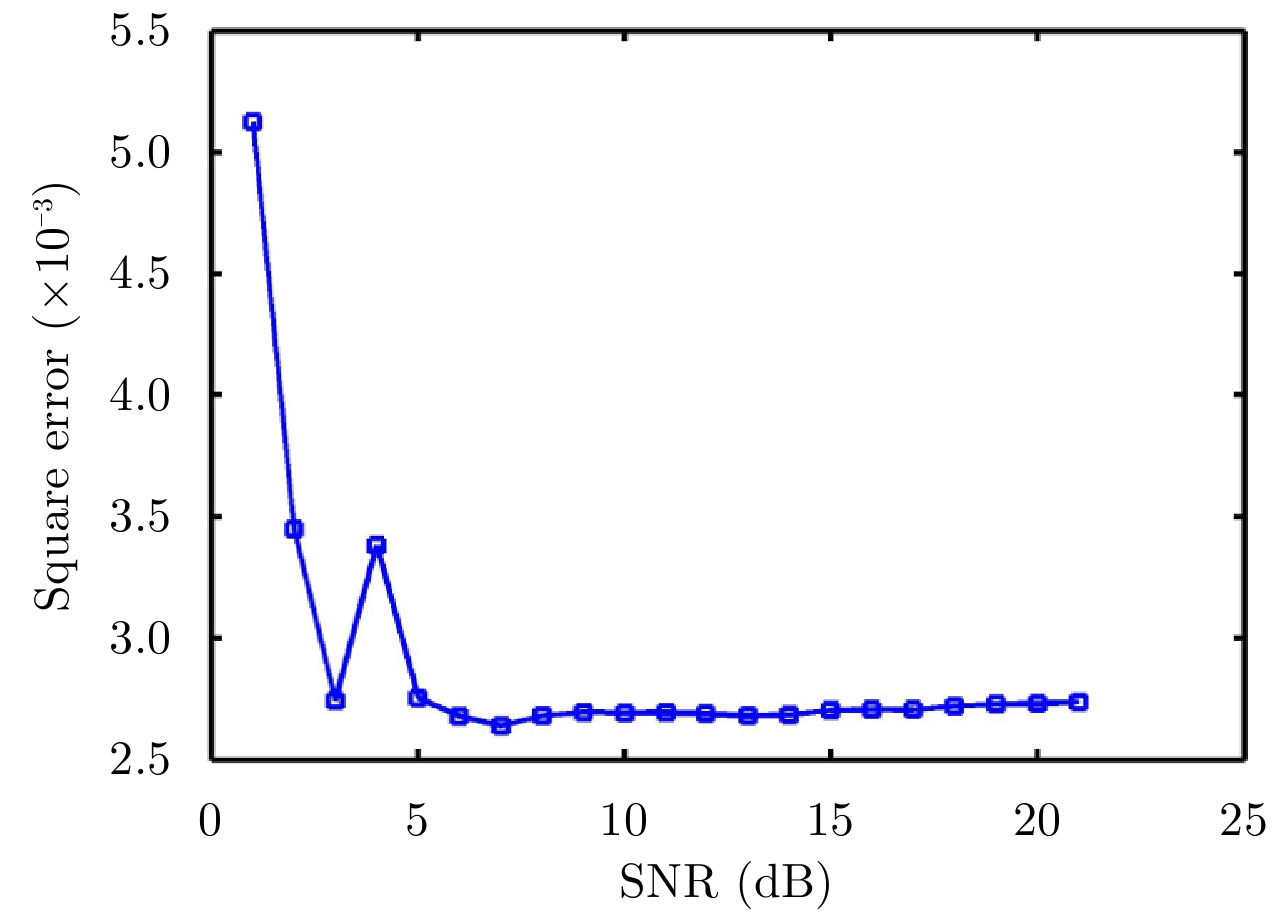
。图7所示为不同信噪比条件下目标旋转角速度的估计效果,由图可见,在信噪比较高时,估计效果比较稳定,受噪声影响较小。
4.1.2 图像配准实验结果
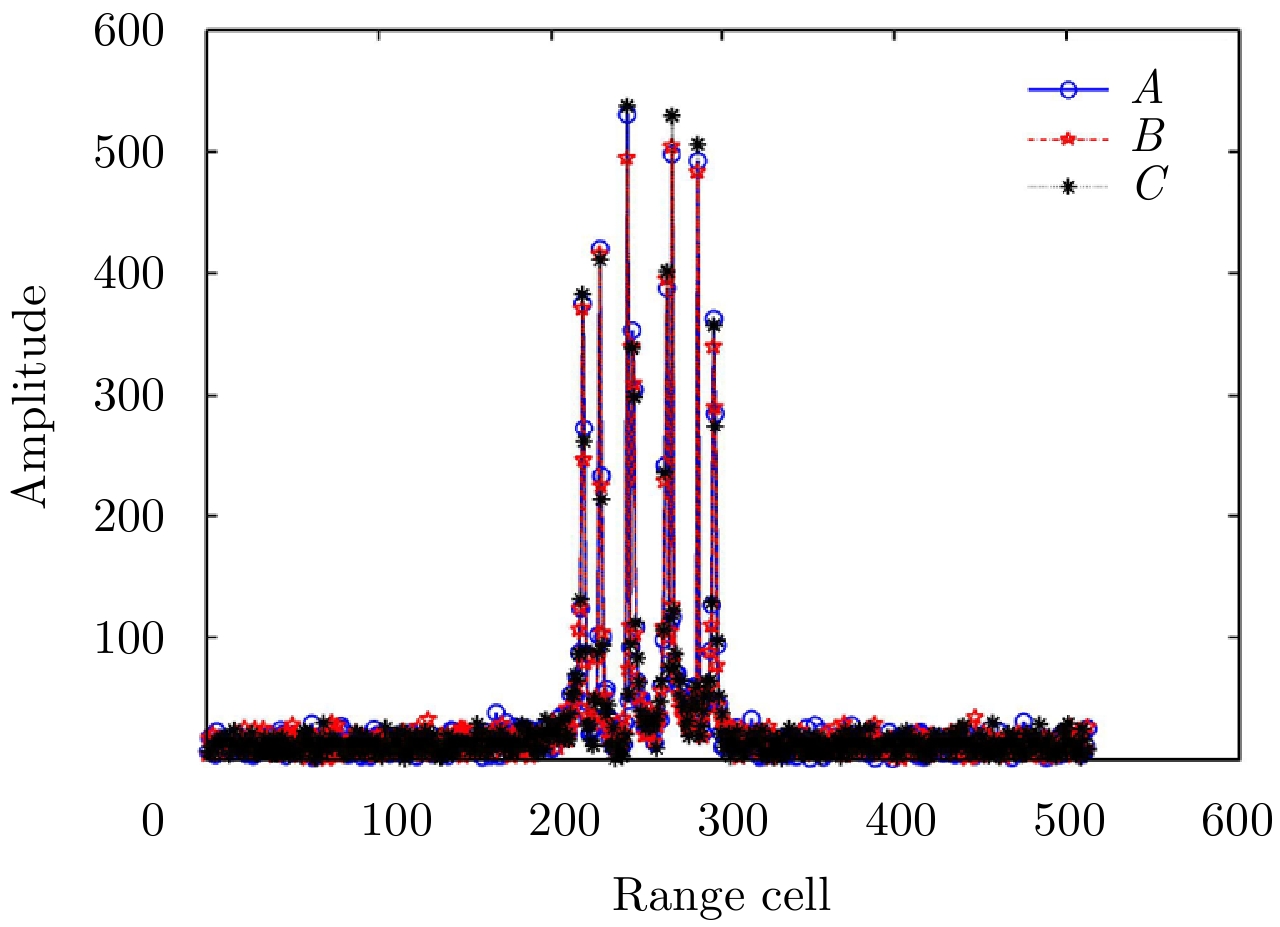
图8所示为各天线经过波程差补偿的回波进行距离压缩得到的目标的1维距离像。显然,3部天线得到的3幅1维距离像极其相似,强散射点基本位于相同的距离单元,忽略噪声的影响,可以认为距离向上基本实现配准。另外,图9给出了雷达A, B和C回波的第50次脉冲对齐之后1维距离像的比较结果,峰值点表示散射点位置,并且峰值对齐效果较好,可见散射点在距离向基本实现精确对齐。
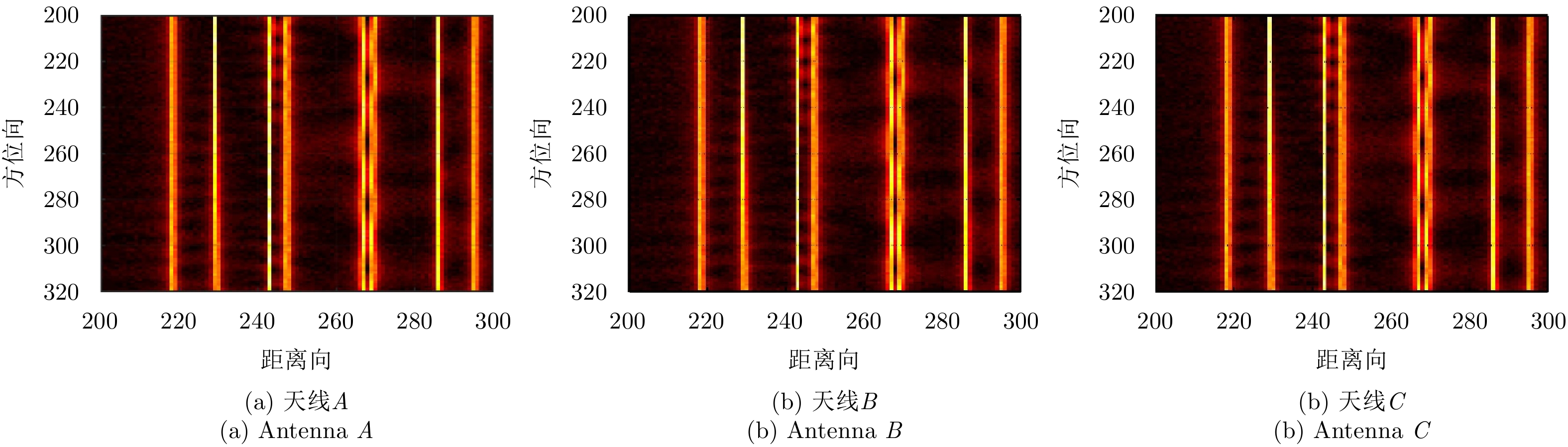
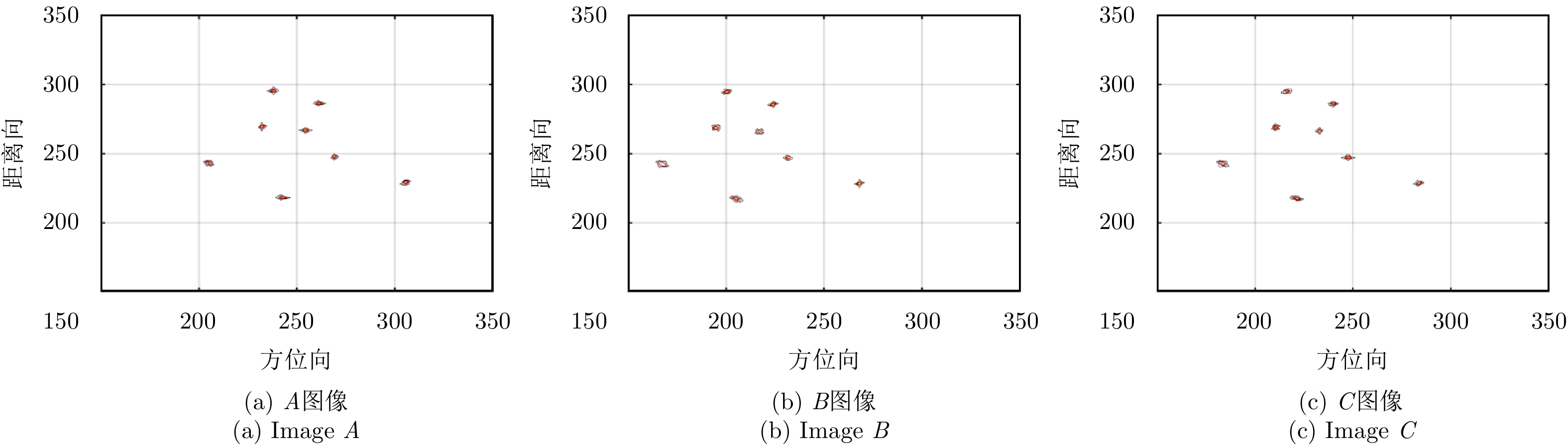
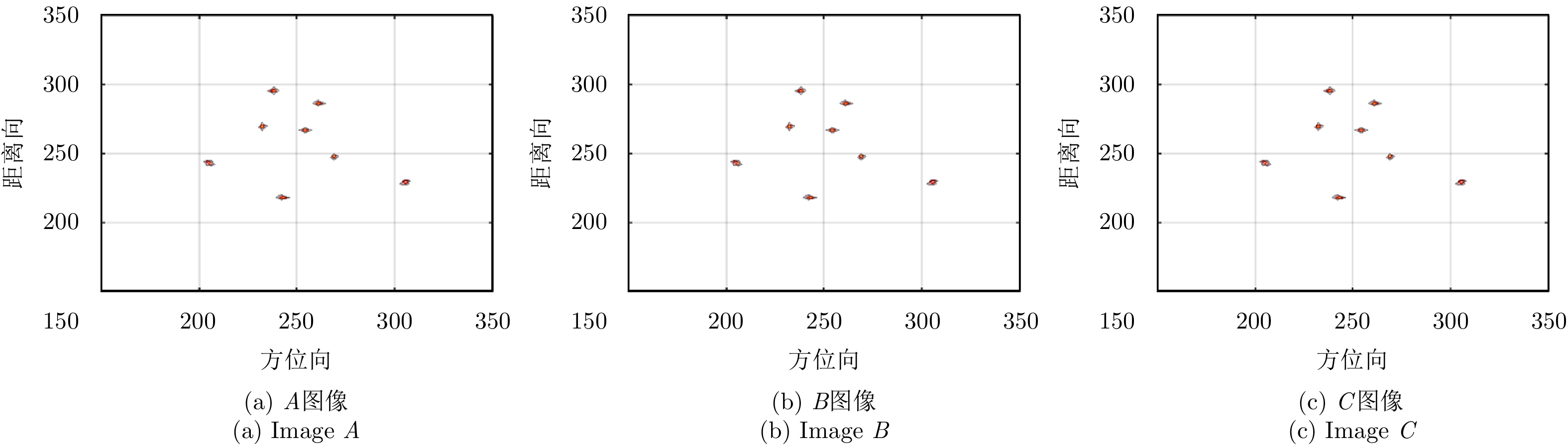
对目标回波的1维距离像进行方位向压缩可以得到目标的2维ISAR图像,3部天线分别各自对目标所成的未进行配准的ISAR图像如图10所示。由于3部天线观测目标的视角不同,且仅仅雷达A发射电磁波,从而雷达B, C接收到的回波的波程与雷达A接收到的回波的波程不同,从而3幅图像会有一定的差别。由图10可见,3幅ISAR图像在距离向没有明显的平移,但是在方位向有明显的错位,即3幅ISAR图像各散射点之间未对齐。考虑到ISAR图像间的错配主要是因为目标上各散射点到不同雷达具有一定的波程差,因此提出一种基于波程差补偿的ISAR图像配准方法。经过所提出的回波域的波程差补偿方法的处理之后,3部天线所成的ISAR图像如图11所示。观察所成图像可以发现无论是在距离向还是方位向,3幅ISAR图像之间均未发生明显的错位。通过峰值检测进一步提取配准之后的ISAR图像当中的强散射点的位置,如表2所示。括号中前一个数为散射点所在的方位向位置,后一个数为散射点在距离向的位置。显然,各强散射点在3幅ISAR图像当中的位置都是一样的,图像间的失配准被消除,即A, B, C 3幅图像完成配准。
表 2 (Tab. 2

表 2 基于波程差补偿方法配准的ISAR图像中各散射点位置
Tab. 2 Locations of scatterers after image registration based on the proposed method
| 散射点标号 |
天线A
|
天线B
|
天线C
|
| 1 |
(247,218) |
(247,218) |
(247,218) |
| 2 |
(279,229) |
(279,229) |
(279,229) |
| 3 |
(229,243) |
(229,243) |
(229,243) |
| 4 |
(260,248) |
(260,248) |
(260,248) |
| 5 |
(253,267) |
(253,267) |
(253,267) |
| 6 |
(242,269) |
(242,269) |
(242,269) |
| 7 |
(256,286) |
(256,286) |
(256,286) |
| 8 |
(244,295) |
(244,295) |
(244,295) |
|
表 2 基于波程差补偿方法配准的ISAR图像中各散射点位置
Tab.2 Locations of scatterers after image registration based on the proposed method
|
4.1.3 InISAR 3维成像实验结果
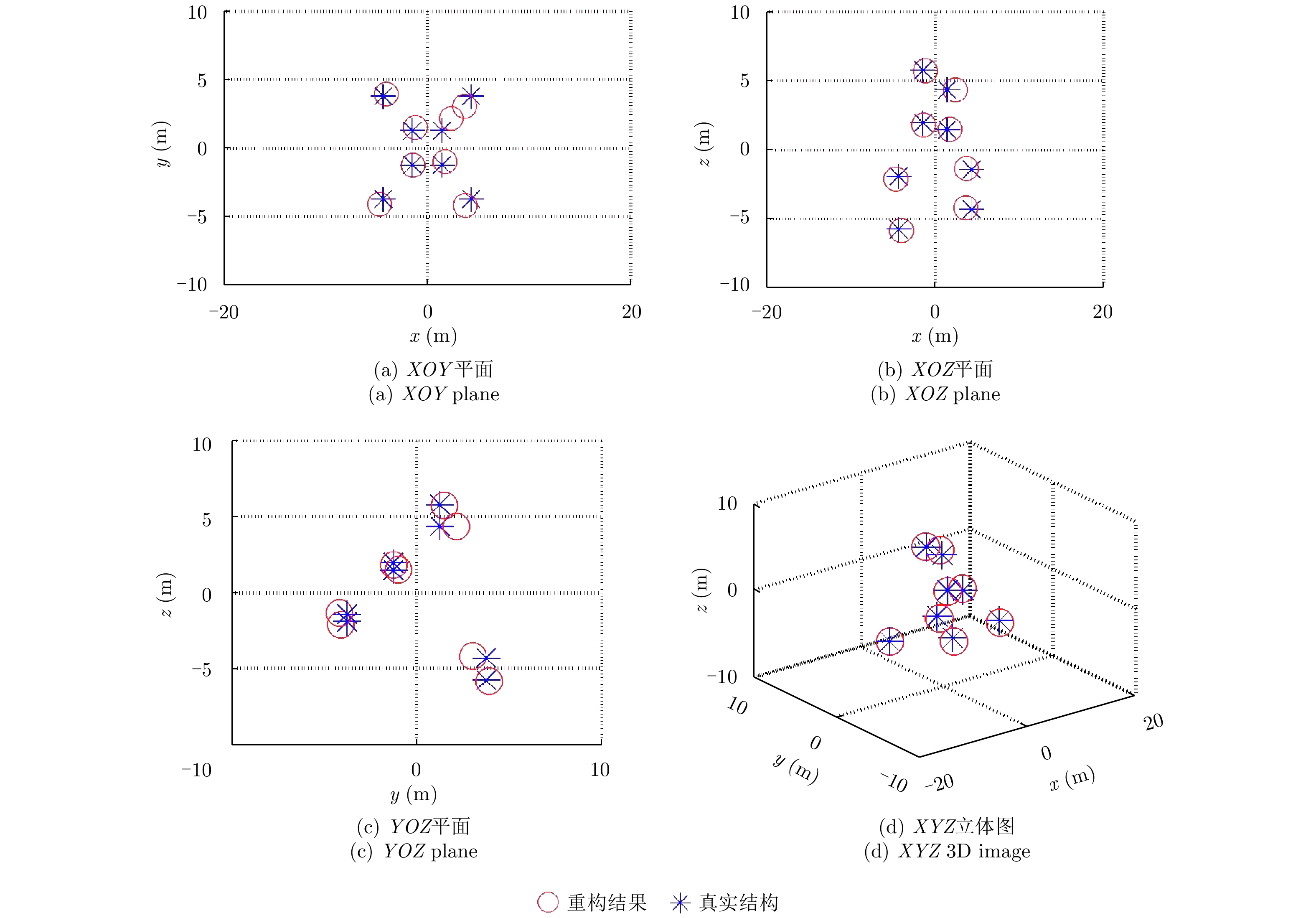
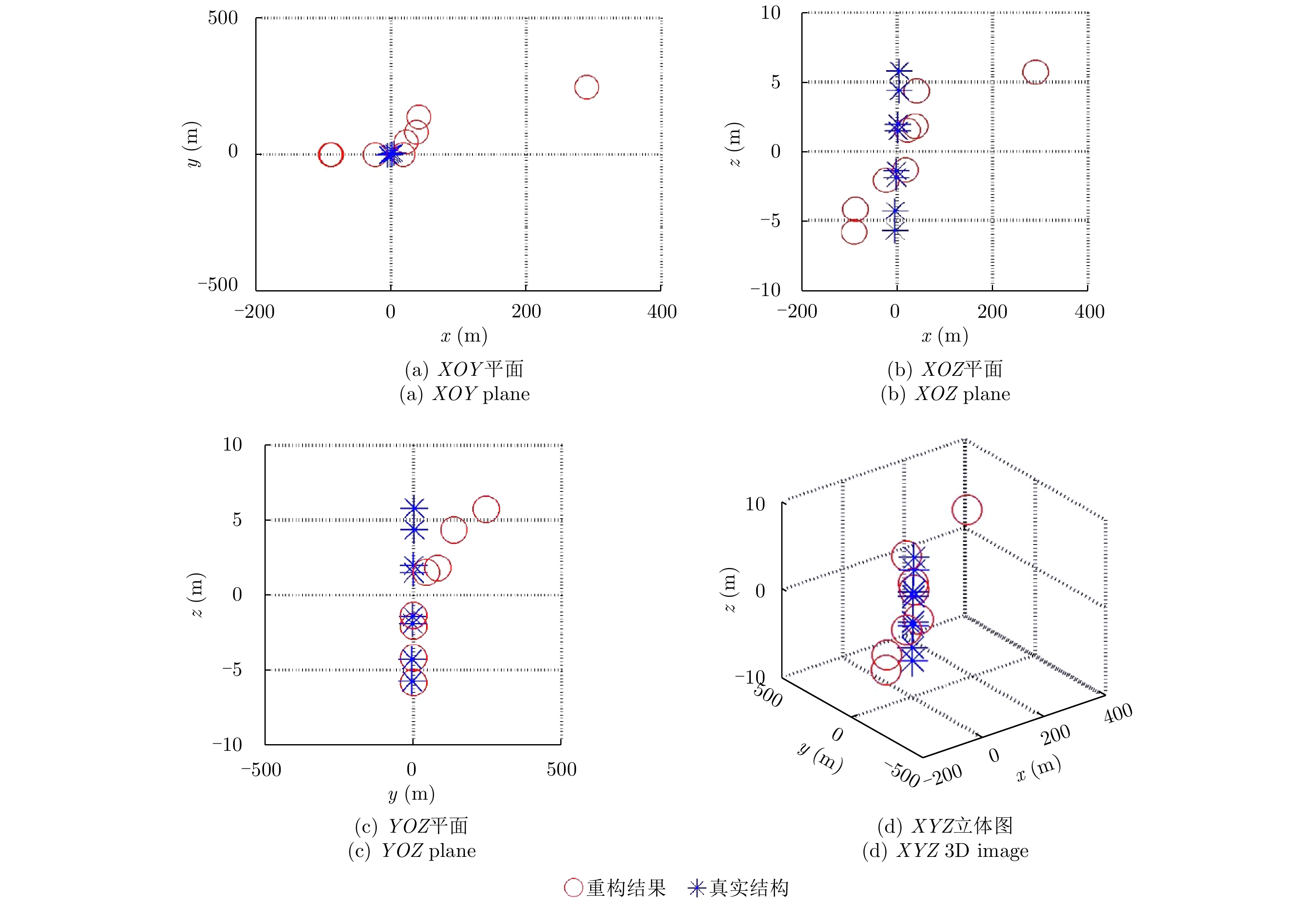
因为ISAR图像配准仅仅是干涉ISAR 3维成像的中间步骤,在完成ISAR图像配准之后还需要进行干涉处理,并根据式(32)和式(33)求解得到目标上各散射点的x坐标和z坐标,y坐标根据各散射点径向距离即可得到。最终,目标的干涉ISAR 3维成像结果如图12所示,其中蓝色“*”点表示目标的真实结构,红色圆圈“○”表示使用波程差补偿方法得到的3维成像结果。其中,红色圆圈与对应的蓝色“*”点的
$\left( {x,y,z} \right)$
3个坐标的差的平均值为0.3034。可见,提出的方法可以很好地实现L型天线结构中3部天线所成ISAR图像的配准,并得到比较好的3维成像结果。
4.2 基于相关系数的图像配准方法实验结果
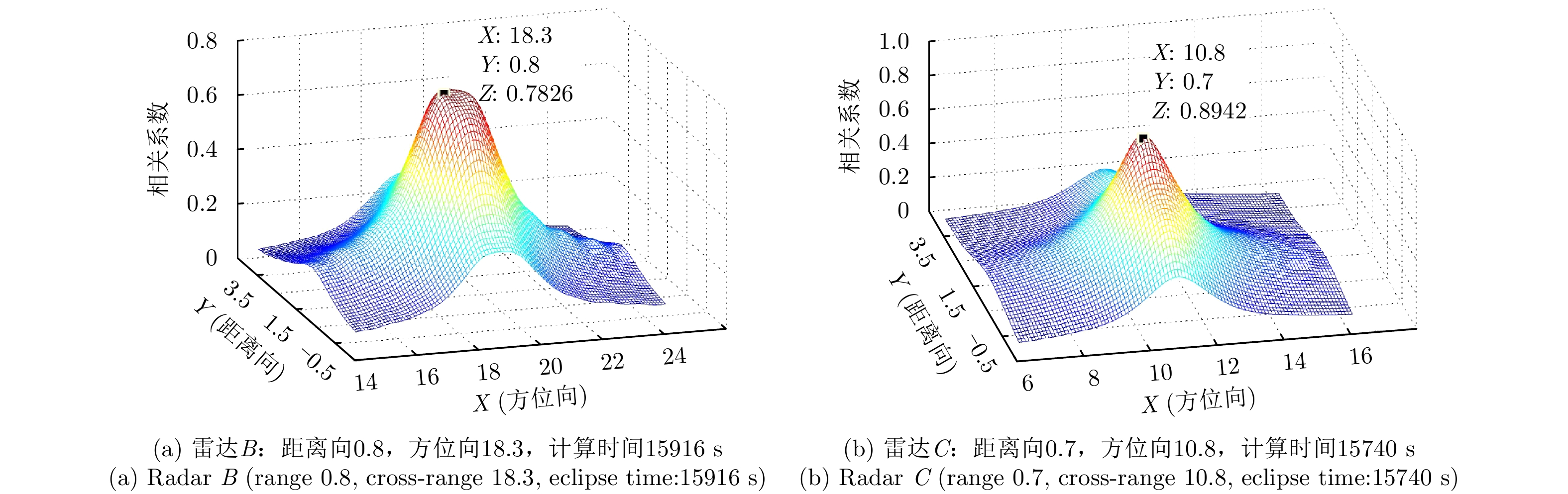
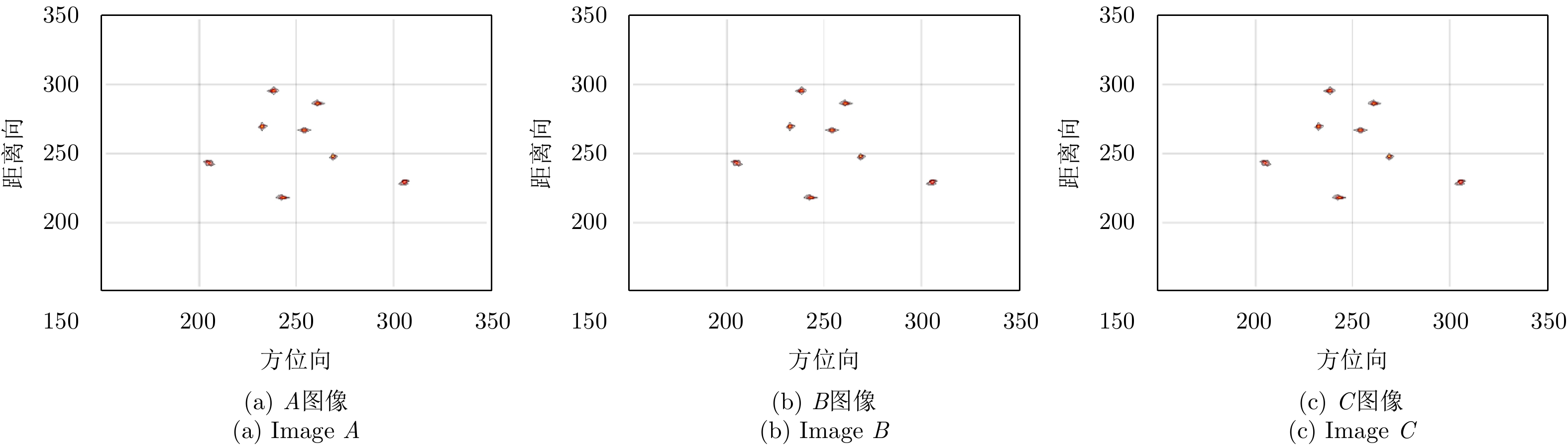
按传统RD成像方法对回波依次进行距离向脉冲压缩,包络对齐,初相校正,方位向脉冲压缩得到目标的ISAR图像。然后分别对B和C的图像逐步进行距离向和方位向的平移,并计算相关系数。该仿真实验在设备参数为Intel(R) Core(TM) i7 7700 CPU @ 3.6 GHz and 16 GB RAM计算机的MATLAB环境中进行,相关系数计算结果如图13所示。其中A, B相关系数的计算用时为15916 s, A, C相关系数的计算用时为15740 s;当B图像距离向平移量为0.8,方位向平移量为18.3时,A和B图像的相关系数达到最大;当C图像距离向平移量为0.7,方位向平移量为10.8时,A和C图像的相关系数达到最大。在实验过程中,为了达到十分之一个像素单元的配准精度,需要对原始图像进行10倍插值处理,另外,还需要搜索距离向和方位向的最佳平移量,这将极大地增加相关法的计算量,因此基于相关系数的图像配准方法的计算时间较长。根据B和C图像的最佳平移量对B和C图像进行平移,平移过后的ISAR图像如图14所示,从左至右依次为A, B, C图像。同样,可以使用峰值检测的方法提取出3幅图像中的强散射点,如表3所示。根据表3可知,有的散射点在3幅图像中的位置并不是同一个像素单元,8个强散射点并没有完全对齐,可见相关法的配准精度相对较差。因为ISAR图像中目标所占的区域相对较小,大部分像素单元都是被噪声占据,目标散射信息对相关系数的贡献值相对较小,所以两幅图像的相关系数更有可能被噪声所影响,尤其是在信噪比较低的观测条件下。最终导致基于相关系数的ISAR图像配准方法的配准精度较差,容易形成错配现象。
表 3 (Tab. 3

表 3 相关法配准之后ISAR图像中各散射点位置
Tab. 3 Locations of scatterers after image registration based on correlation method
| 散射点标号 |
A图像
|
B图像
|
C图像
|
| 1 |
(247,218) |
(246,218) |
(247,218) |
| 2 |
(279,229) |
(278,229) |
(278,230) |
| 3 |
(229,243) |
(229,243) |
(229,243) |
| 4 |
(260,248) |
(260,247) |
(260,248) |
| 5 |
(253,267) |
(252,266) |
(253,267) |
| 6 |
(242,269) |
(242,269) |
(241,270) |
| 7 |
(256,286) |
(256,286) |
(256,286) |
| 8 |
(244,295) |
(243,295) |
(244,295) |
|
表 3 相关法配准之后ISAR图像中各散射点位置
Tab.3 Locations of scatterers after image registration based on correlation method
|
目标的干涉ISAR 3维图像结果如图15所示,其中,红色圆圈与对应的蓝色“*”点的3个坐标的差的平均值为45.8529。可见基于相关法的图像配准精度比较差,导致最终的InISAR 3维图像与目标的真实结构相差甚远。综上所述,基于波程差补偿的方法通过在回波域进行波程差补偿消除散射点到不同天线之间的波程差进而实现ISAR图像配准,再进行干涉处理获得目标的3维结构,最终的成像结果表明本文方法的有效性。
4.3 基于波程差补偿的复杂目标的InISAR成像
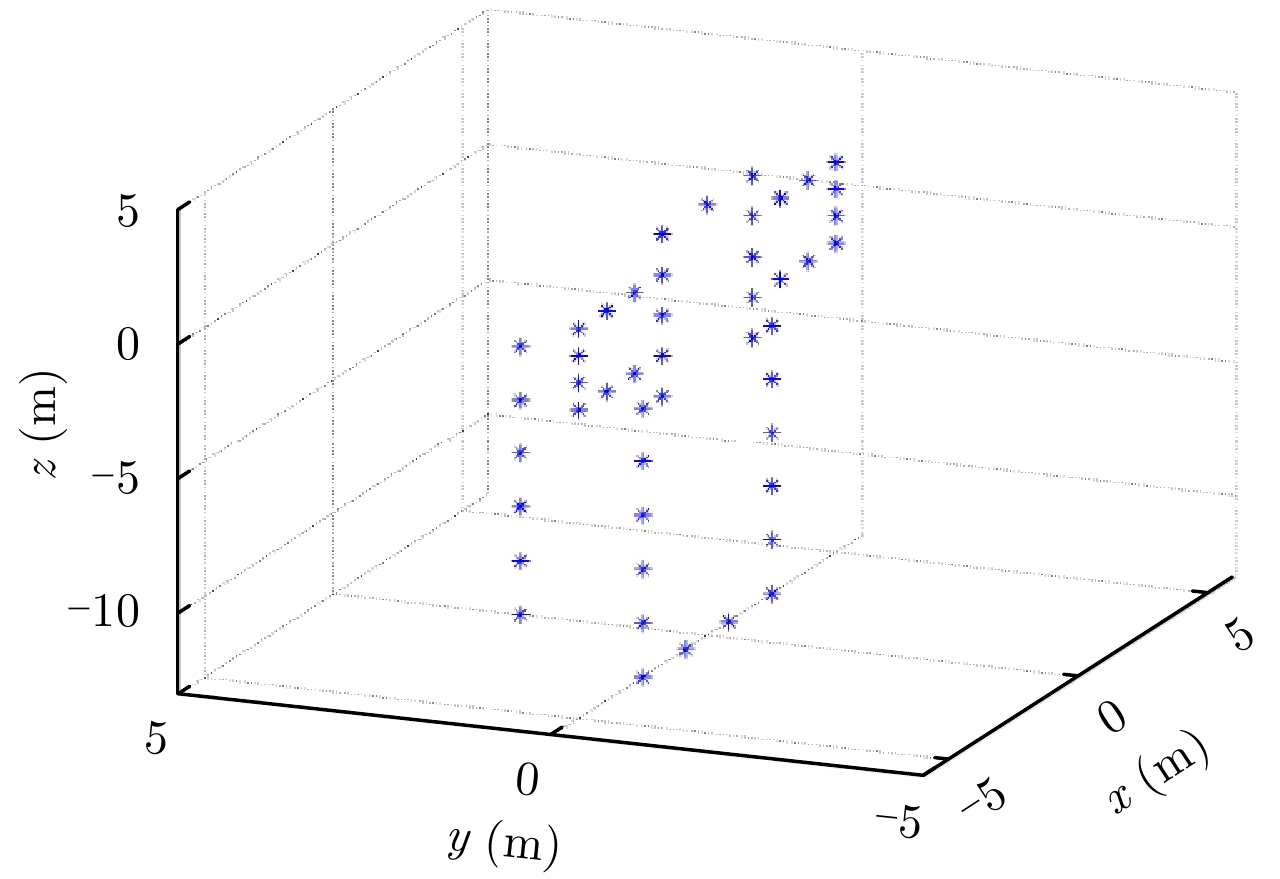
为进一步验证所提出算法的稳定性,此部分用“天宫一号”卫星模型按照上述算法流程进行InISAR成像仿真实验。具体目标结构以及仿真模型如图16和图17所示。
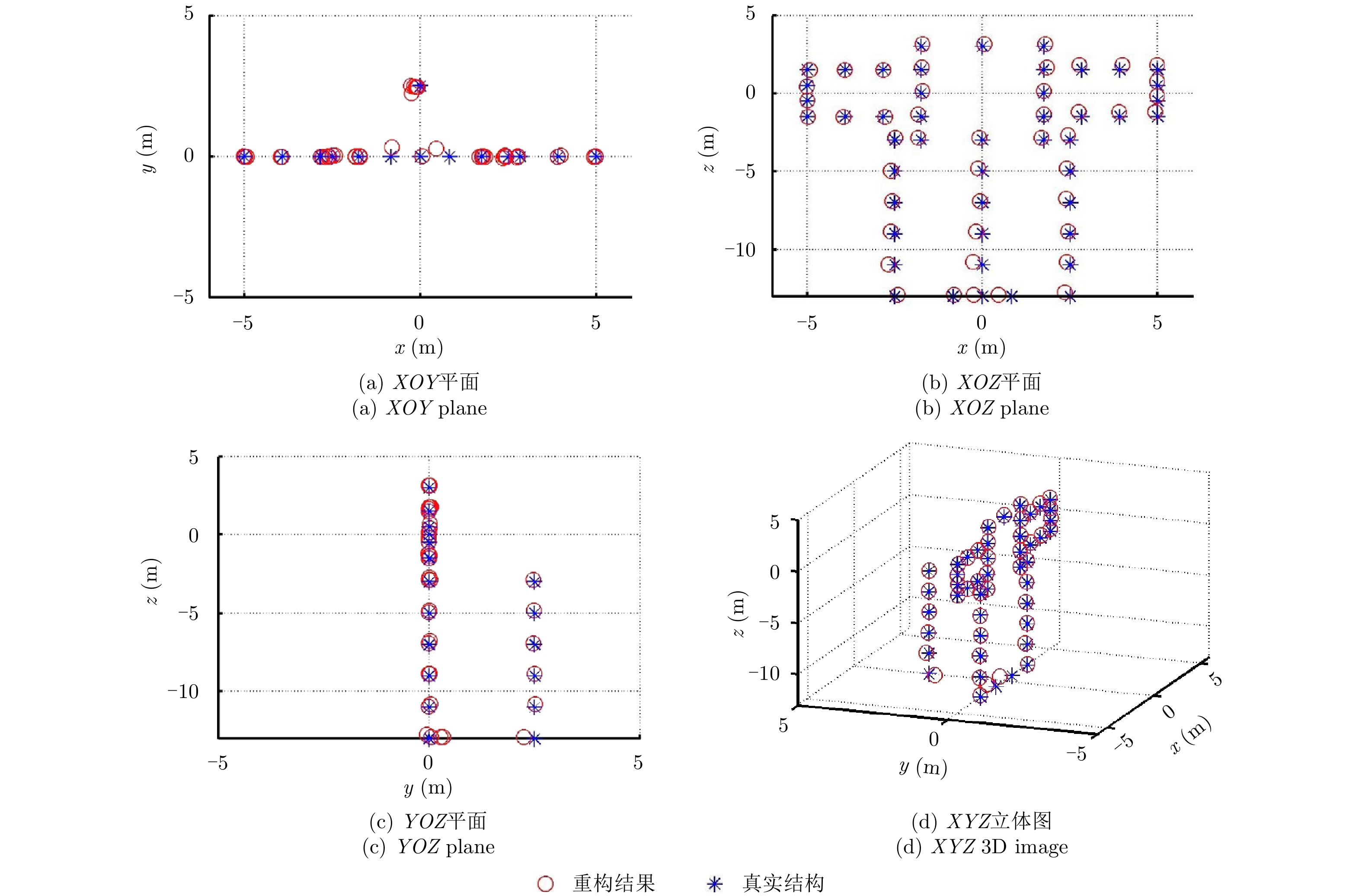
根据上述算法流程,对“天宫一号”散射点模型进行InISAR成像,成像结果如图18所示,其中蓝色“*”点表示目标的真实结构,红色圆圈“○”表示使用波程差补偿方法得到的3维成像结果。因为ISAR图像配准只是InISAR成像的中间步骤,因此这里直接采用最终的InISAR成像结果来衡量算法性能。由成像结果在XOZ平面的投影可见,目标真实结构的投影与成像结果的投影比较一致,成像结果在XOZ平面与真实结构吻合得比较好;再根据YOZ平面的结构可知,干涉结果在y坐标方向上也基本吻合,误差较小,所以,总体而言最终的3维成像质量比较好。可见,所提出的算法对于较复杂的散射点模型也能得出较好的成像效果,由此可见所提出的基于波程差补偿的ISAR图像配准方法可以很好地实现ISAR图像配准,并获得质量较好的InISAR 3维成像结果。
5 结论
本文提出一种基于波程差补偿的ISAR图像配准方法,通过在回波域的相位补偿消除各散射点到不同天线之间的波程差,最终完成ISAR图像的配准。实验结果证明,相比于基于相关系数的ISAR图像配准方法而言,本文方法可以在回波域直接完成ISAR图像的配准,并且配准精度较高,计算负担较轻。最终获得的目标真实的3维成像结果也证实该ISAR图像配准方法更适合被应用于InISAR 3维成像,并进一步通过复杂目标的InISAR 3维成像结构验证了所提出方法的稳定性。
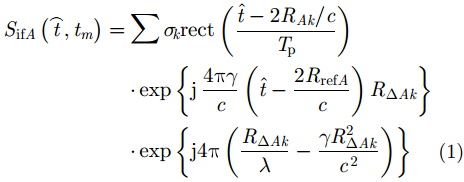
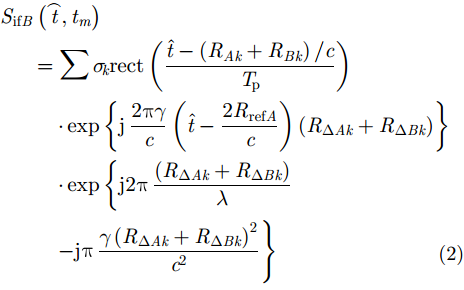
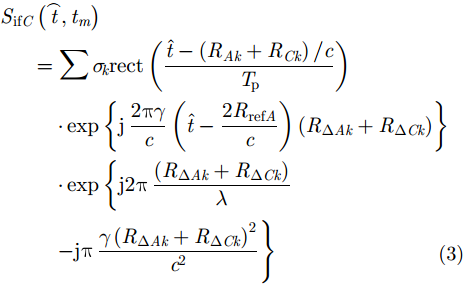
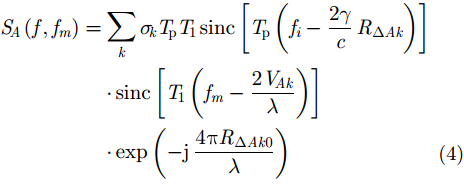
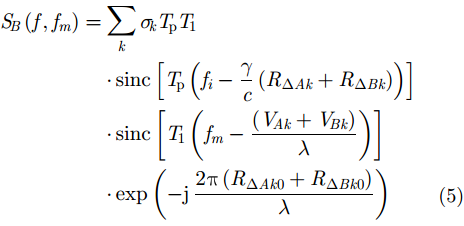
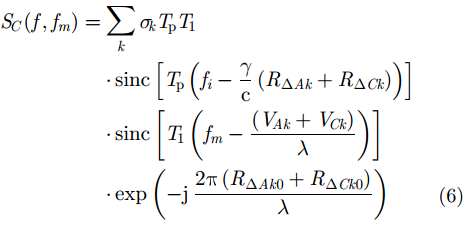
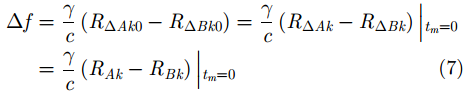
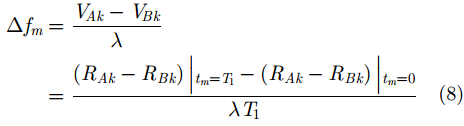
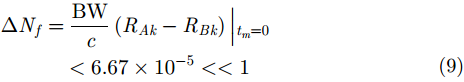
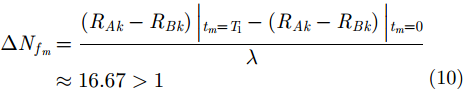
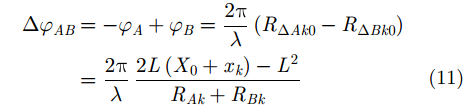
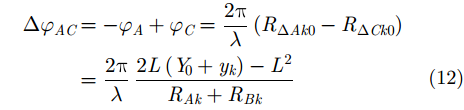
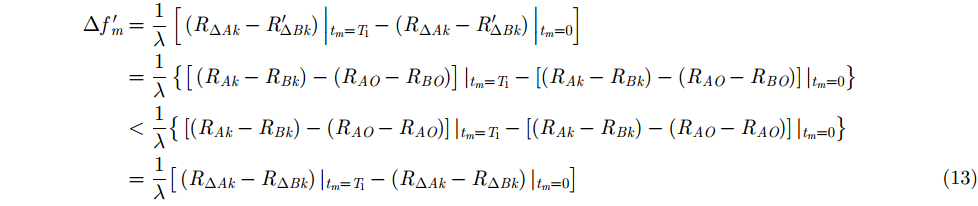
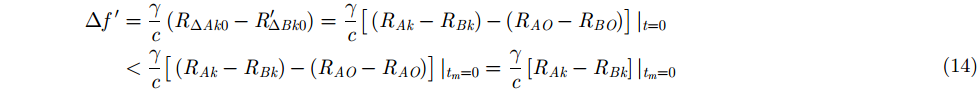
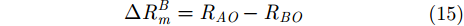
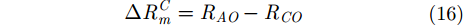
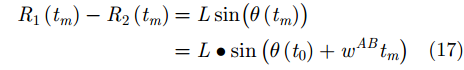
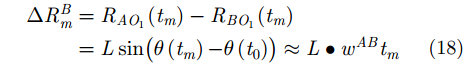
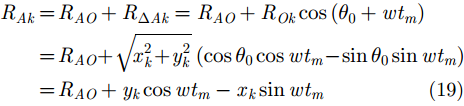
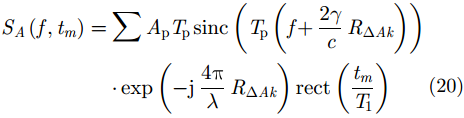
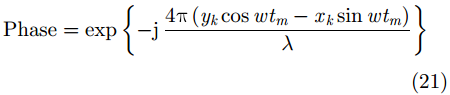
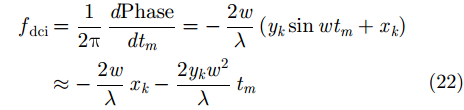
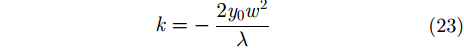
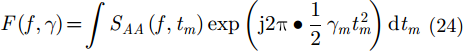
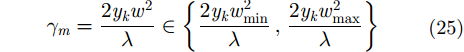
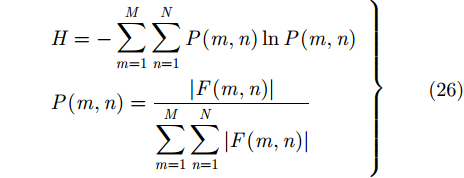
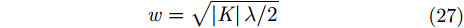
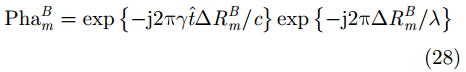
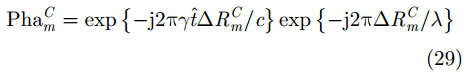
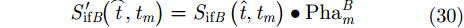
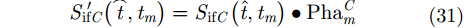
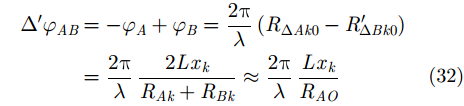
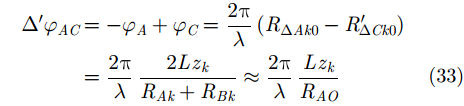

 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)




