② (电磁散射重点实验室 北京 100854)
② (Science and Technology on Electromagnetic Scattering Laboratory, Beijing 100854, China)
在高频区,雷达目标的总散射响应可由多个局部等效散射源响应的相干叠加来描述,这些局部散射源被称为目标的等效散射中心,简称散射中心[1,2]。参数化表示的目标散射中心模型由于具有形式简单、稀疏,且模型参数与几何、物理性质相关等优点,在雷达目标的快速信号仿真[3]、数据压缩[4]、隐身与特征控制[5],以及特征提取与自动目标识别(Automatic Target Recognition, ATR)[6–8]等领域均获得了广泛应用。近年来,随着我国海洋活动日益增加,舰船目标的雷达信号仿真、隐身设计、特征提取与识别等问题受到了越来越多的关注[9–11],同时,考虑到舰船目标属于超电大尺寸目标,又与实际海面环境相复合,因此研究海面舰船目标的散射中心建模方法具有重要的学术和应用价值。
与1维、2维相比,3维散射中心模型不但给出了目标散射中心空间分布的完整描述,而且更加不敏感于目标姿态[12,13]。因此,3维散射中心建模一直是诸多学者感兴趣的研究内容[12–14]。
一般而言,散射中心建模主要包括模型形式选择和模型参数提取两个方面。在模型形式选择方面,最简单的散射中心模型是理想点散射中心模型,它假设散射中心位置与幅度不随频率与视向角变化,但该假设只在窄带、小角度情况下成立。对于大带、宽角度情形,实际目标的散射中心一般不能视为常数,需要将频带和角度细分成小区间,在每个小区间内理想点散射中心是适用的。尽管为了能解析描述散射中心的位置和幅度随频率与视向角的变化,目前已经陆续提出了包括Prony模型[6]、GTD模型[15]、属性散射中心模型[16]、典型体散射特征模型[17]等,但这些模型形式在不同程度上比理想点散射中心模型更为复杂,对于诸如舰船之类的电大尺寸复杂目标3维散射中心建模来说,模型参数的估计将变得非常困难。因此,目前工程上最常用的仍是最简单的理想点散射中心模型。在模型参数提取方面,目前提出的方法主要包括频域方法和图像域方法。频域散射中心提取算法包括谱估计[18]、贪婪算法[19]、正则化方法[20]、基追踪方法[21]等,但这类方法随着参数空间维数增加,参数估计性能和效率均大大降低。图像域散射中心提取方法主要通过雷达成像处理以及图像峰值提取来获取散射中心分布,已提出的方法包括CLEAN[22]、分水岭[23]等方法。一般来说,与频域方法相比,图像域方法提取效率较高,但散射中心位置估计受限于雷达图像分辨率,其精度难以提高。此外,文献[24]还提出将频域方法与图像域方法相结合 ,可以在一定程度上解决图像域方法参数提取精度低的问题。尽管如此,由于工程上常常需要获取全角域的3维散射中心分布,图像域方法需要通过仿真计算获得较高采样率的扫频扫角雷达散射截面(Radar Cross Section, RCS)数据,用于生成3维雷达图像,计算量较大,即使采用具有较高效率的高频计算技术[9,25–28]来获取扫频扫角RCS数据,也仍然难以满足实际工程应用的需要。
上世纪90年代,Bhalla等人[13]提出了射线管积分技术,实现了在单频单视角下直接计算获得雷达目标3维图像,避免了较高角度采样率的RCS计算,极大地减小了计算量,提高了计算效率,为实现海面舰船目标3维散射中心快速建模提供了一种有效途径。本文针对大型海面舰船目标,将射线管积分方法与处理舰船海面耦合的“4路径”方法相结合,采用简化的海面模型和“准镜面”处理方法,提出一种海面舰船目标3维散射中心快速建模方法。并且,以典型海面舰船目标为例,对比3维散射中心重建的与直接仿真计算的1维距离像和2维图像,验证了本文所提方法的有效性。同时,比较本文算法与传统方法生成3维散射中心的计算耗时,以此说明本文算法在计算效率上的优势。
2 舰船海面复合3维散射中心建模原理本文所提3维散射中心建模方法主要包括ISAR成像和散射中心提取两部分。前一部分采用“4路径”模型和射线管积分技术来实现,其主要原理见2.1节;后一部分采用CLEAN算法实现3维散射中心提取,其原理见2.2节。
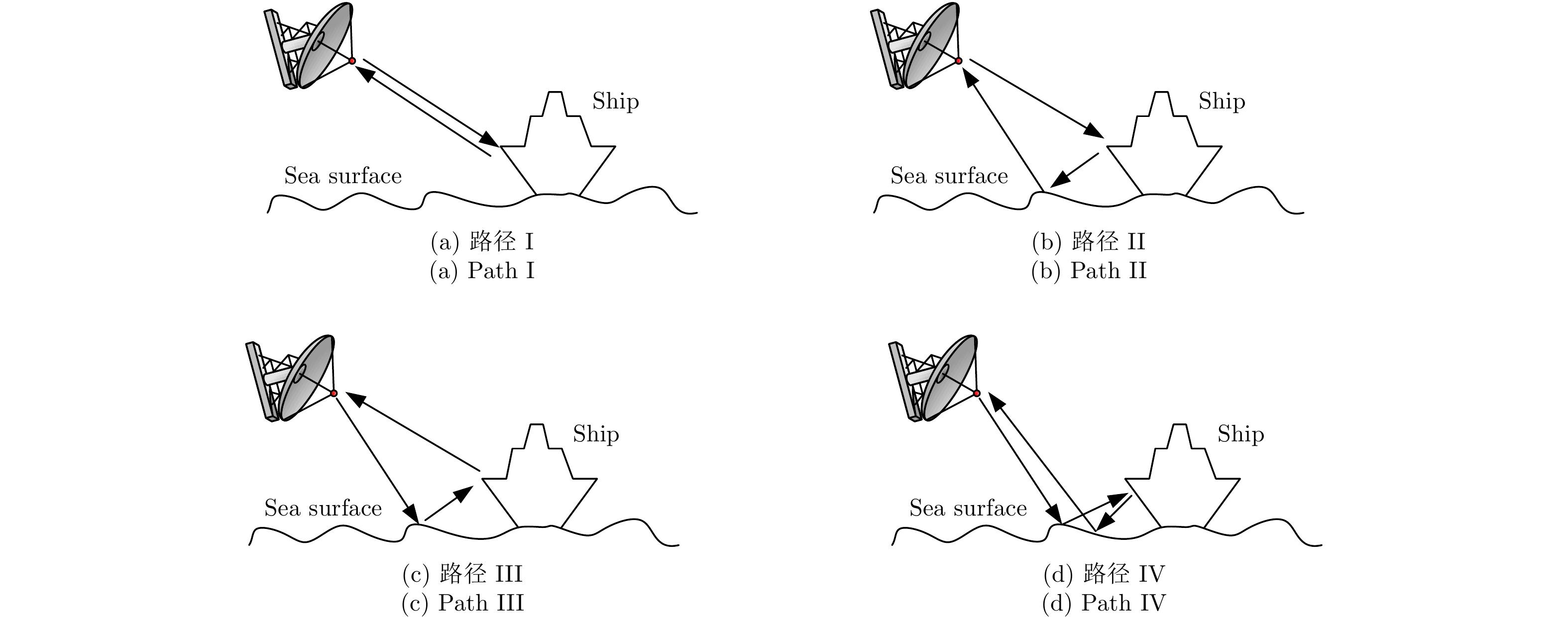
2.1 基于“4路径”模型和射线管积分技术的海面舰船目标3维快速ISAR成像2001年,Johnson等人[29,30]提出了“4路径”模型用于计算粗糙面上目标的本体散射,以及目标与粗糙面之间的耦合散射。图1为“4路径”模型计算目标与海面复合散射的示意图,考虑4种多路径散射机理:图1(a)为目标本体的散射贡献(路径I);图1(b)为目标-海面的2次反射贡献(路径II);图1(c)为海面-目标的2次反射贡献(路径III);图1(d)为海面-目标-海面的3次反射贡献(路径IV)。其中路径II, III, IV对应目标-海面间的耦合散射,涉及粗糙海面散射。传统基于海面面元的弹跳射线(Shooting and Bouncing Ray, SBR)方法[9,29,30],需要追踪海量的射线,计算量巨大。本文参考董纯柱等人[27,28]提出的“准镜像”处理方法,该方法无需建立海面面元模型,能够高效地计算随机微粗糙环境表面上复杂目标的高频电磁散射特性。
|
图 1 海面目标散射的“4路径”模型 Fig.1 “Four Path” model for target-surface coupling scattering |
根据“4路径”模型,雷达接收天线位置接收到的电场矢量是来自4条回波路径上场量的叠加
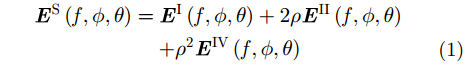
|
其中,
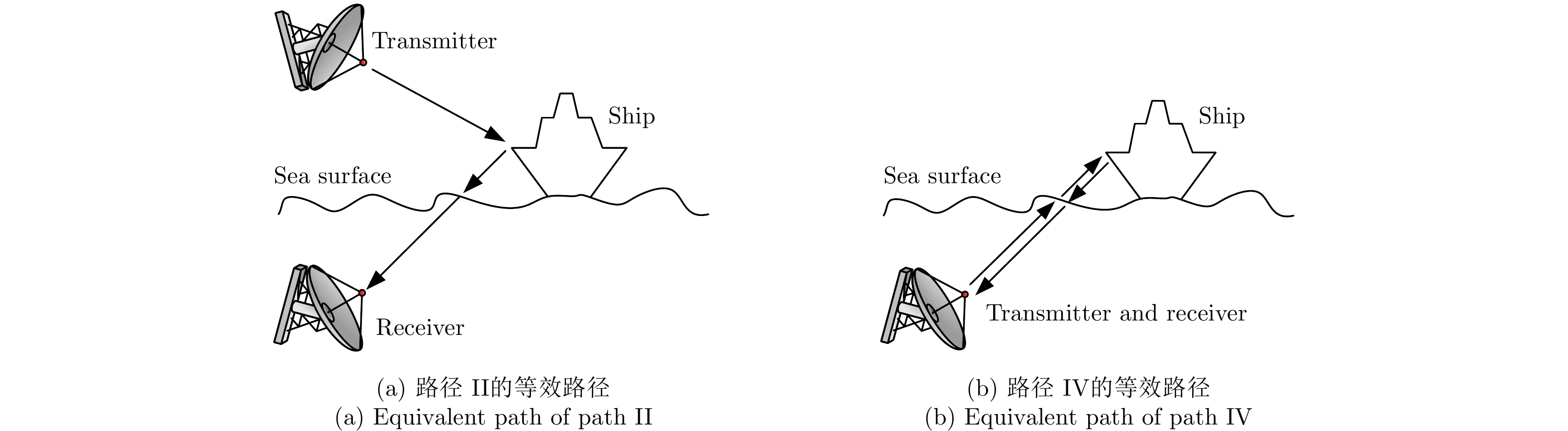
根据“准镜像”处理方法[27,28],路径II可等效为接收机位置不变而发射机移到海平面镜像位置处双站探测的几何配置(如图2(a)所示),原来的单站散射计算问题转换成双站散射计算问题;路径IV可等效为发射机与接收机均移到海平面镜像位置处单站探测的几何配置(如图2(b)所示),原来的单站散射计算问题转换成雷达在镜像位置的单站散射计算问题。
|
图 2 “准镜像”处理方法 Fig.2 “Quasi-image” method |
基于SBR技术的高频电磁计算方法可实现各路径散射场的快速计算。该方法发射大量的射线到目标区,对射线在目标表面发生1次或多次的弹射进行追踪,通过几何光学(Geometrical Optics, GO)计算每根射线的电磁场传输,最后对目标表面GO场所激发的感应电流进行远场物理光学(Physical Optics, PO)积分求得远场散射场的镜面反射贡献;采用等效边缘电流(Equivalent Electrical Current, EEC)方法计算舰船的边缘绕射贡献;最后将两者求和得到目标的总散射场或RCS(详细计算过程可参考文献[9,25–28])。
与通常计算远场RCS的目的不同,本文旨在快速计算3维像用于3维散射中心提取。根据“射线管积分”方法,目标的3维ISAR像可以通过先对每根射线场远场贡献分别进行3维ISAR像处理再对得到的“子图像”进行求和而获得,即
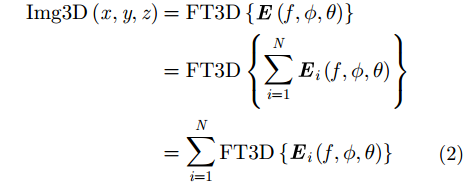
|
其中,下标i表示射线的序号,
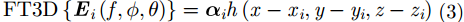
|
其中,
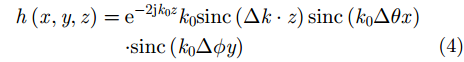
|
其中,
于是,应用式(2)、式(3)到式(1),可得“4路径”模型表达的目标3维ISAR图像的解析表达式

|
其中,
由式(5)可知,本方法是在单频、单视角下计算得到的3维像,与传统的基于扫频、扫角回波数据的成像算法相比,计算效率将大大提高。另外,采用Sullivan格式近似式(5)的卷积运算可进一步提高计算效率[13]。
海面的复反射系数

|
其中,
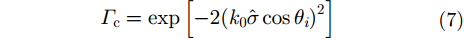
|
其中,
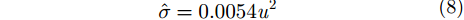
|
其中,
在获得3维ISAR像后,需要进一步提取3维散射中心的位置与幅度。本文基于一种图像峰值提取CLEAN算法,从3维ISAR像中提取目标的3维散射中心参数[13]。原理是在3维像中从大到小地逐次“剔除”峰值区域的值,“剔除”峰值区域遵循的公式为:
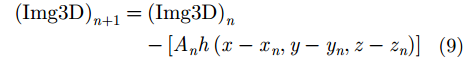
|
其中,
CLEAN算法遵循的步骤是:
(1) 寻找3维像中的最大像素值,记录该像素值的位置
(2) 按照式(9)在最大值附近按照点扩散函数分布将最强点能量“剔除”,得到残余图像;
(3) 寻找残余图像中的最大像素值,记录该像素值的位置
(4) 反复循环(2)和(3)的操作,直到峰值提取值低于预先设定好的阈值,然后退出循环;
(5) 上述步骤所得一系列的位置
基于前面所述原理,本节给出一种海面舰船目标3维散射中心快速建模算法。图3给出了本算法的主要流程图。主要流程如以下步骤:

|
图 3 海面舰船目标3维散射中心快速建模算法流程图 Fig.3 The flow chart of fast algorithm to establish 3-D scattering center model for ship target over sea surface |
(1) 输入雷达观测条件参数(频率、方向角、极化等)、舰船几何面元模型、粗糙海面参数(海面均方高、风速等);
(2) 分别针对路径I, II, IV,进行射线弹跳几何追踪,根据2.1节所述方法计算各个射线的相位中心参数:
(3) 针对路径I,通过GO-PO-EEC方法计算舰船目标本体的单次、多次镜面反射以及边缘绕射机理所对应的各射线远场贡献的复幅度值
(4) 利用式(5)获得海面舰船目标的3维ISAR像数据
(5) 利用CLEAN算法(式(9))对海面舰船目标3维像数据进行峰值提取处理,获得海面舰船目标3维散射中心分布
传统的图像域散射中心建模方法为获取高分辨率雷达目标图像,需进行较大数据量的扫频扫角目标RCS仿真计算,比较耗时。上述算法由于采用了射线管积分、“4路径”模型、修正Fresnel系数模型等技术,不但可实现在单频单视角下直接计算雷达目标3维图像,而且简化了目标与海面相互耦合计算,因而极大地减小了计算量,提高了计算效率。在下一节中将通过实际算例对算法的精度和计算效率进行验证。
4 实验、分析与验证基于前面所提算法,以典型舰船目标为例,计算海面舰船目标3维散射中心分布,通过比较3维散射中心重建的与直接仿真的1维距离像、2维ISAR来验证本文算法的有效性,并通过与传统基于FFT方法生成3维散射中心的计算耗时对比,说明本文所提算法在计算效率上的优势。评估本文算法精度的电磁仿真方法将采用基于SBR技术的高频电磁计算技术[9,25–28]。
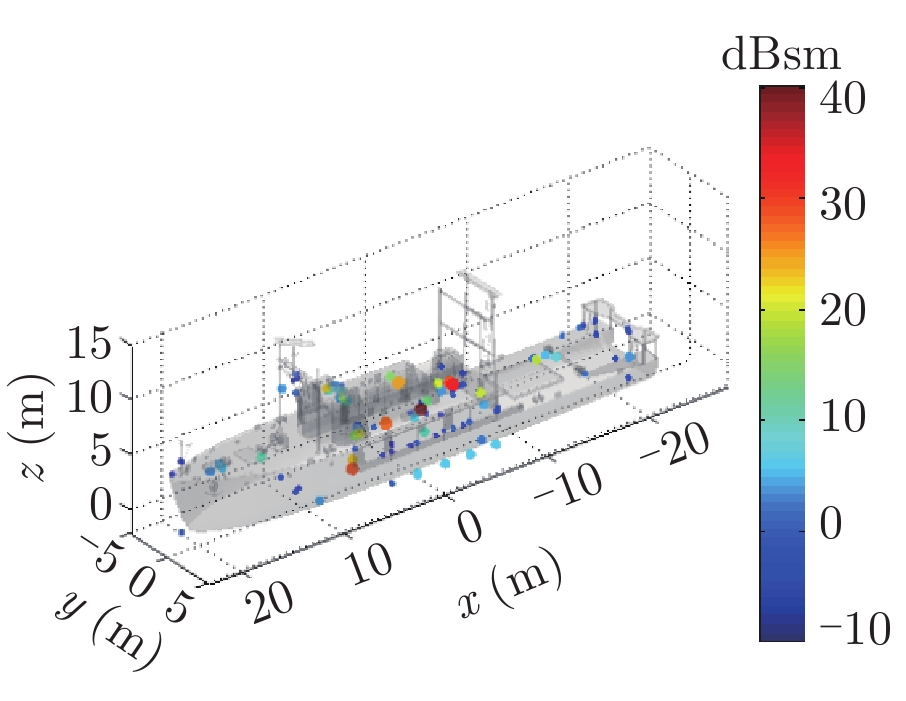
图4所示为海面上典型舰船目标的几何场景示意图,舰船的尺寸为长45.0 m、宽7.9 m、高13.7 m。图5给出了典型舰船目标的面元模型,面元数为105。针对该模型,利用本文所提算法计算了4种海情(0~3级)、不同方位角(0°~360°,1°间隔)下海面上舰船目标3维散射中心分布。其它计算条件:频率10 GHz、入射角70°和极化VV保持固定不变。本算例中计算3维ISAR像的采样间隔为0.156 m×0.156 m×0.156 m, CLEAN算法提取散射中心采用的绝对阈值为0 (dBsm)。值得一提的是,每种海情下全方位的3维散射中心数据只有4 MB大小,却可以实时地生成任意方位角下任意分辨率的2维像(或SAR/ISAR图像)。因此,3维散射中心模型可用于雷达图像数据的压缩与快速生成。

|
图 4 海面舰船几何场景 Fig.4 The geometrical scene of a ship target over sea surface |

|
图 5 舰船目标网格模型 Fig.5 The Mesh-grid model of the ship |
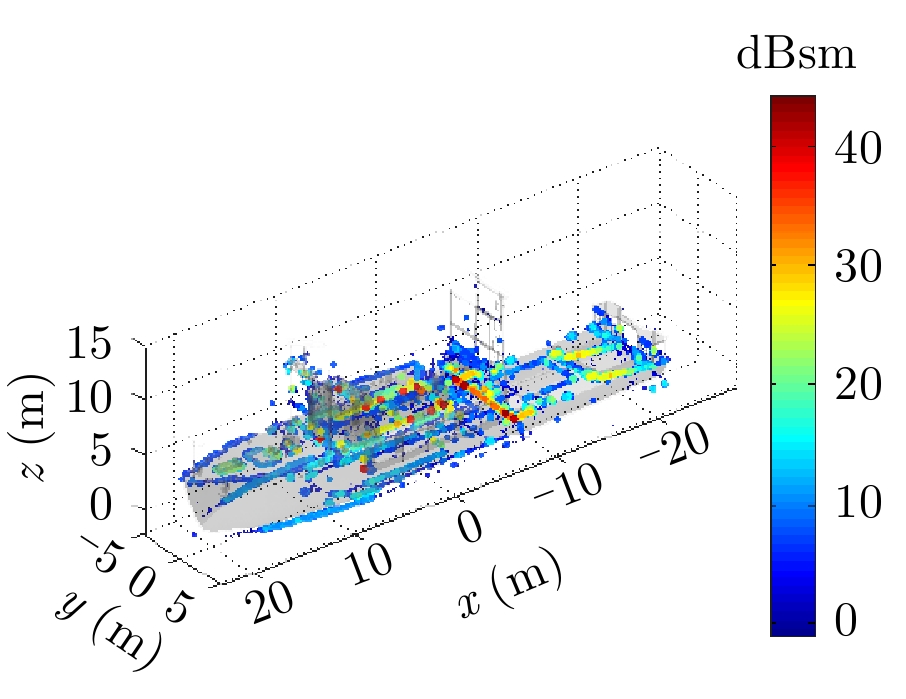
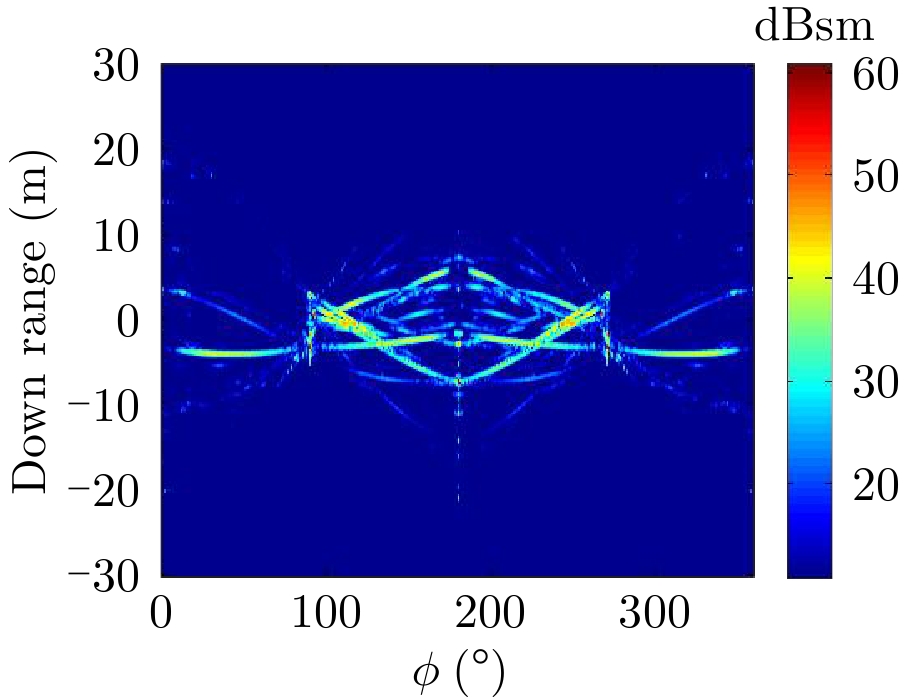
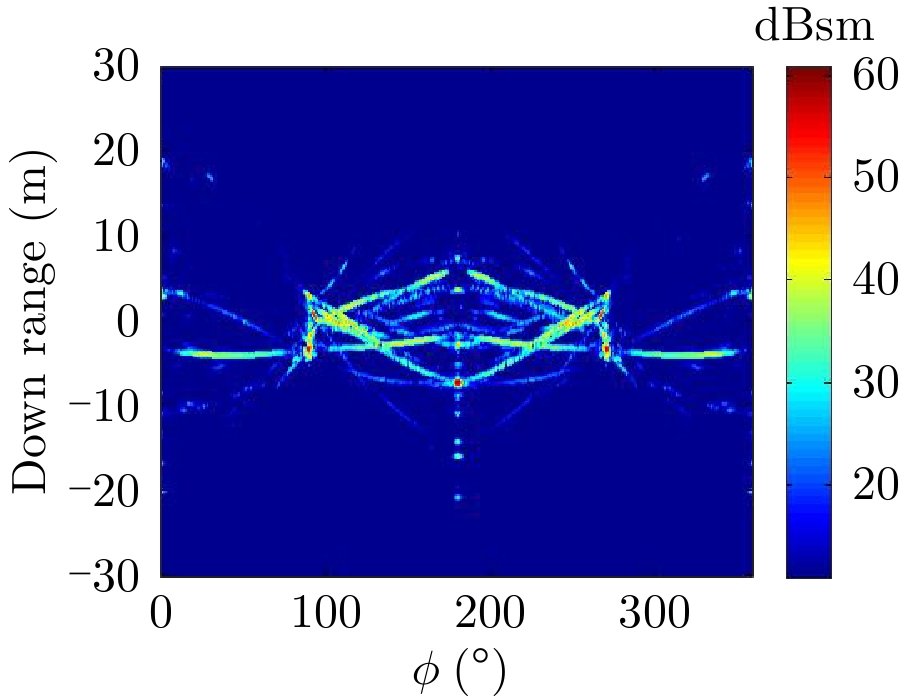
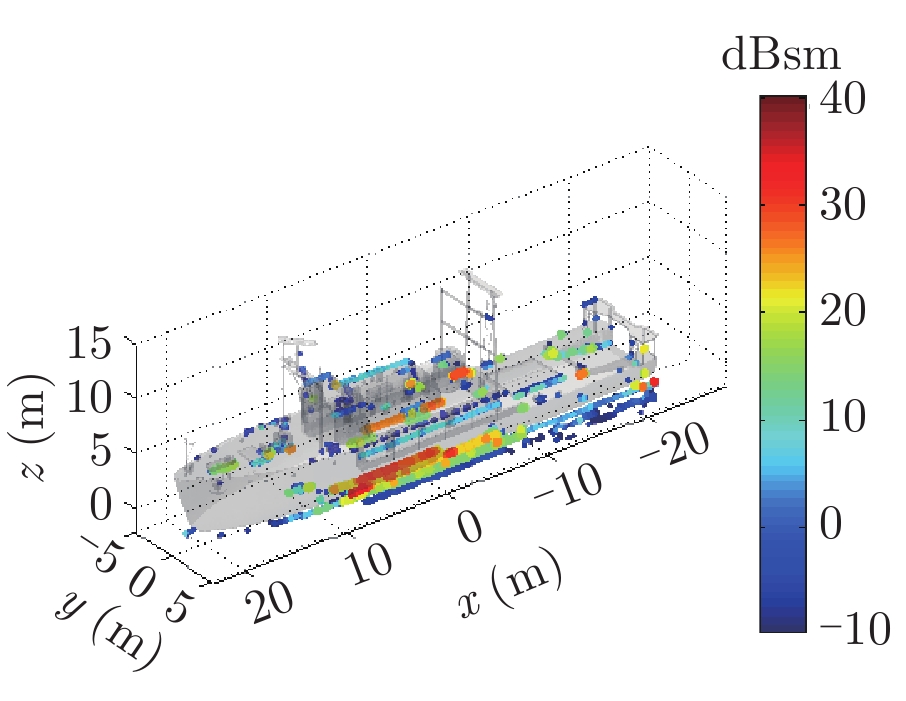
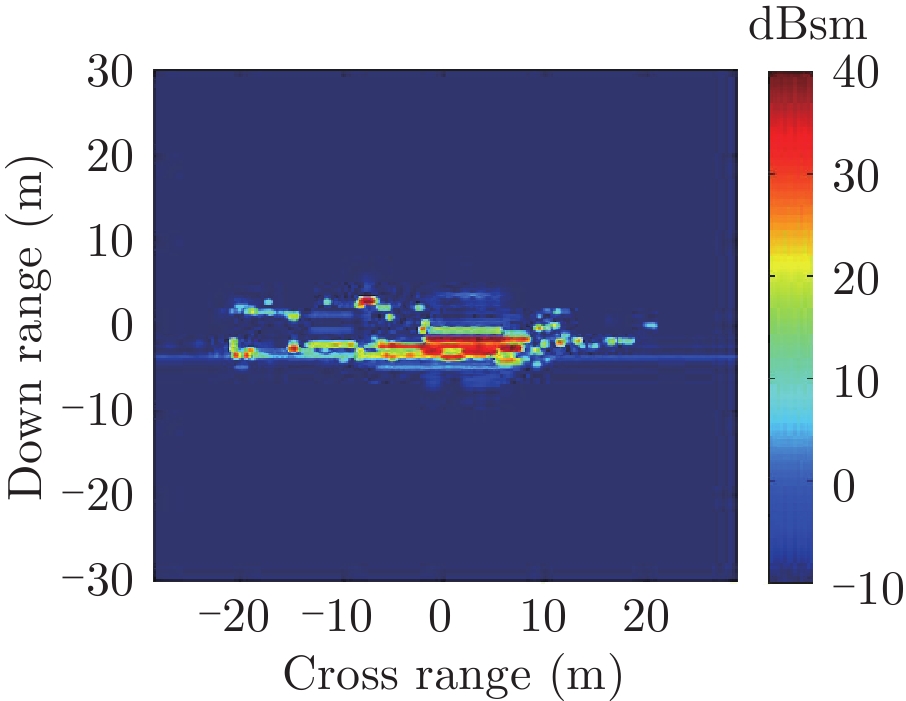
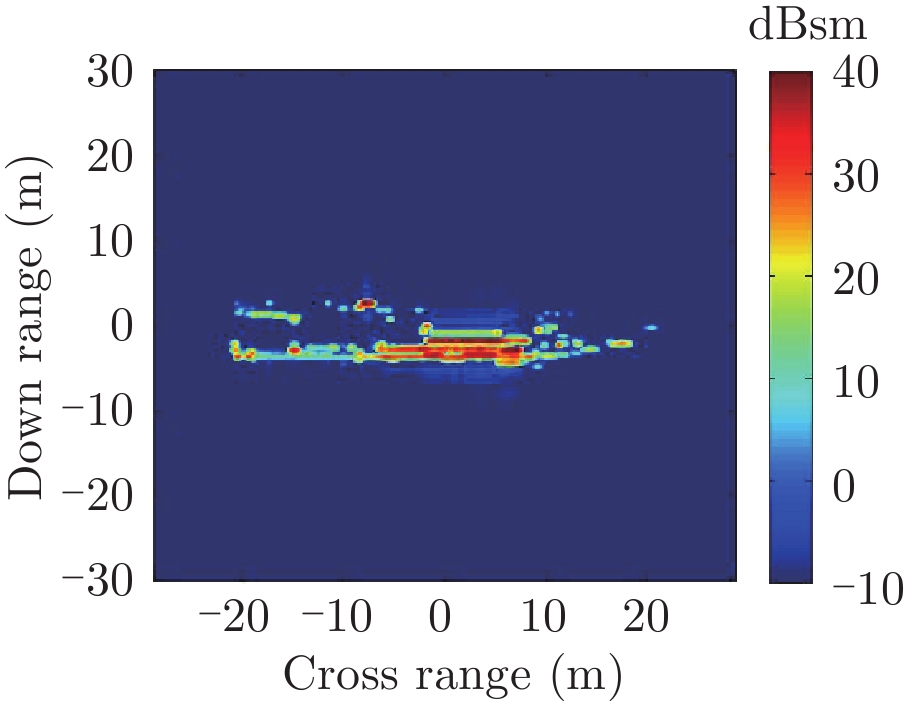
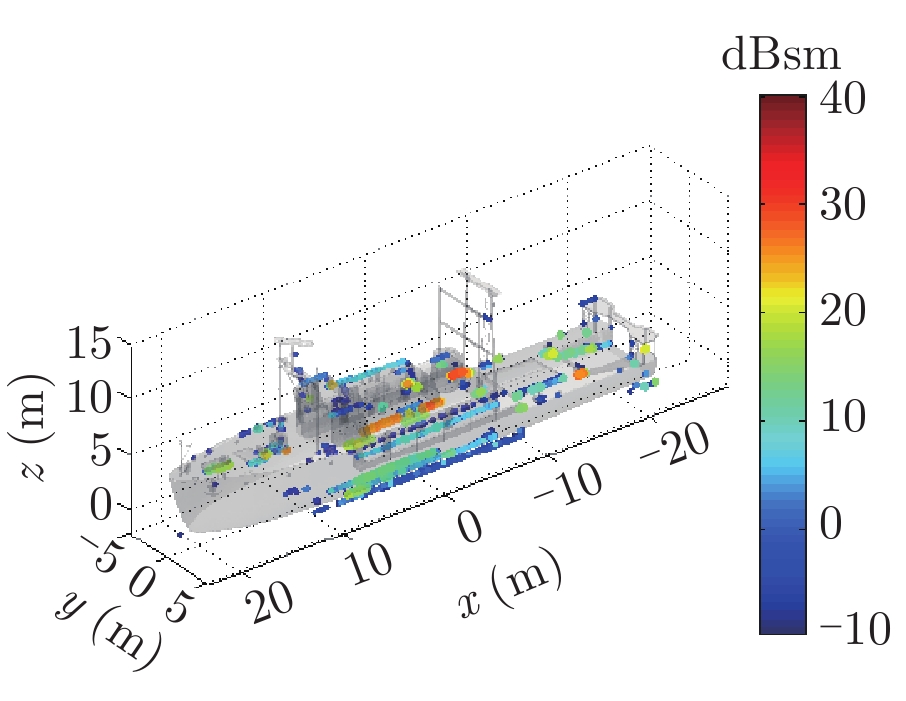
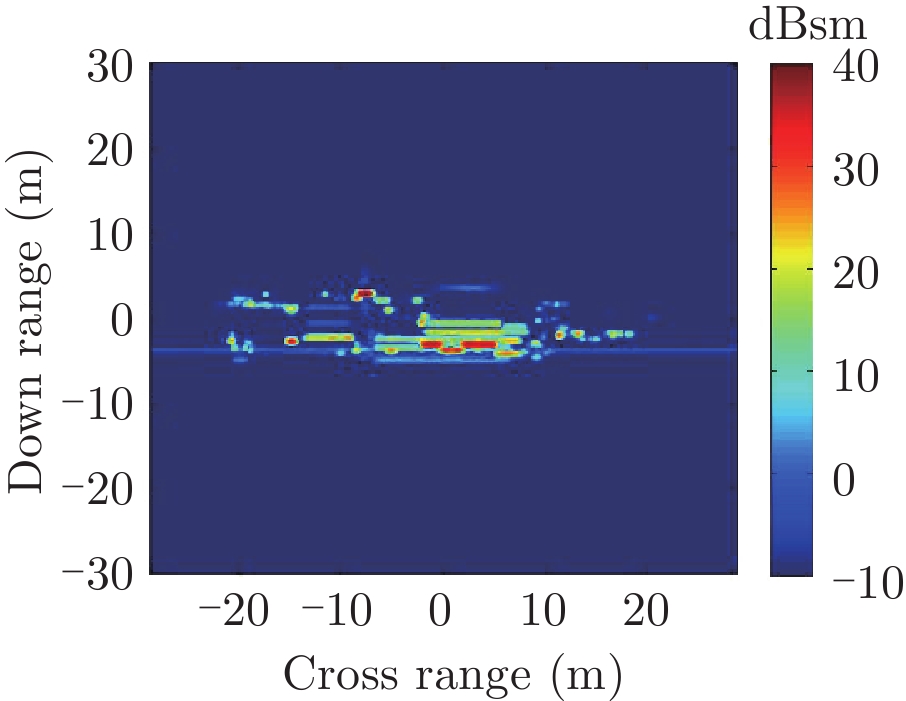
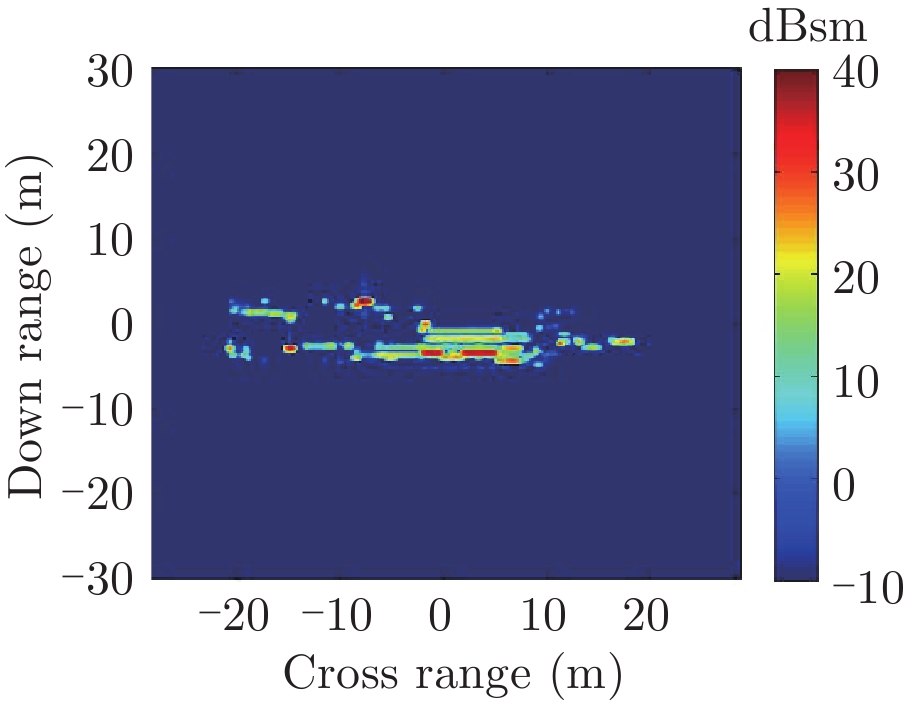
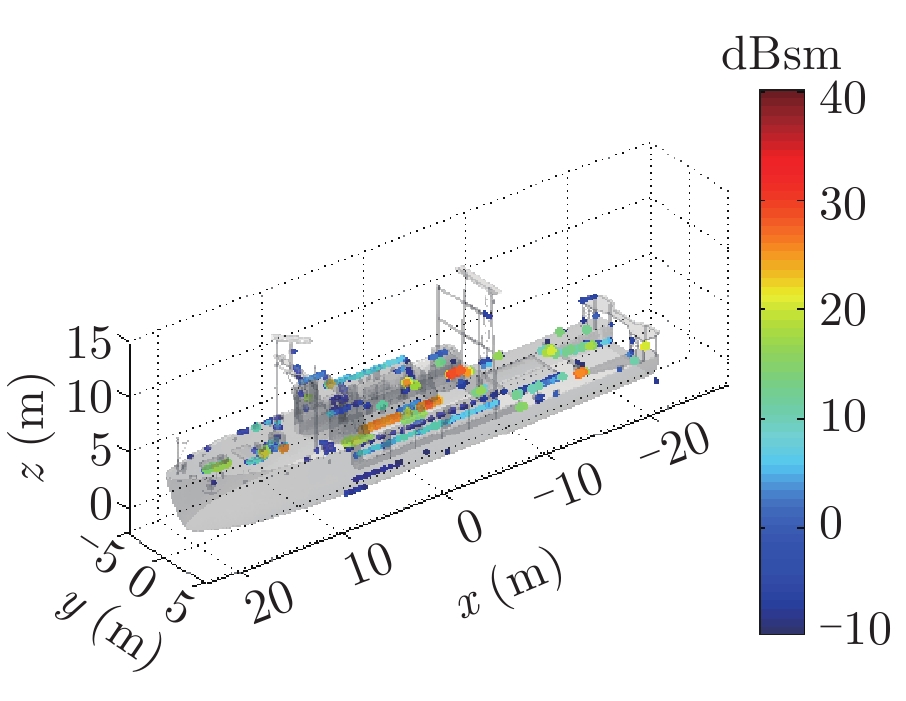
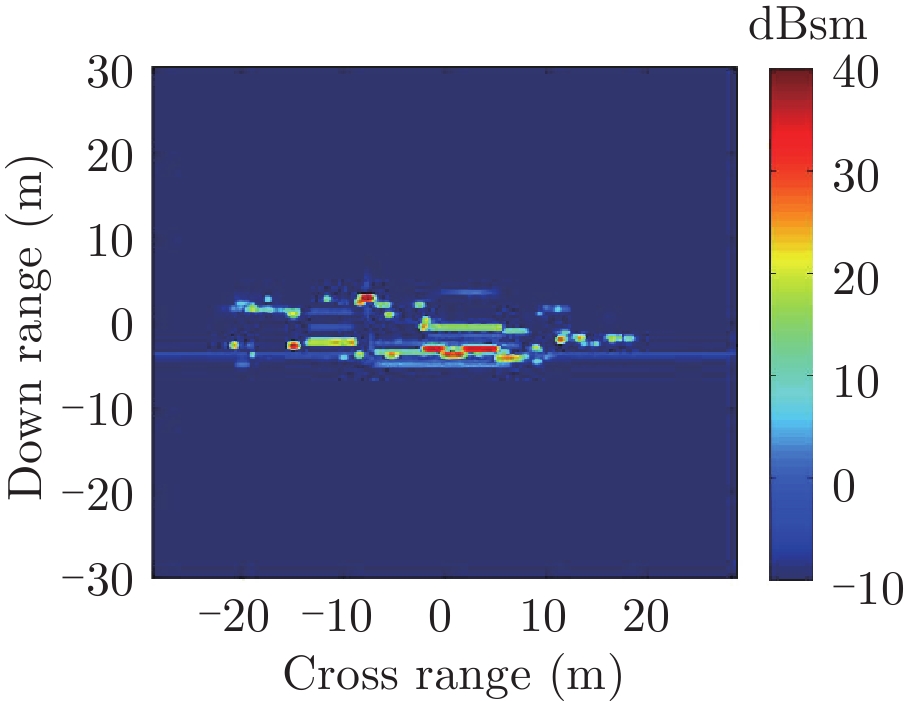
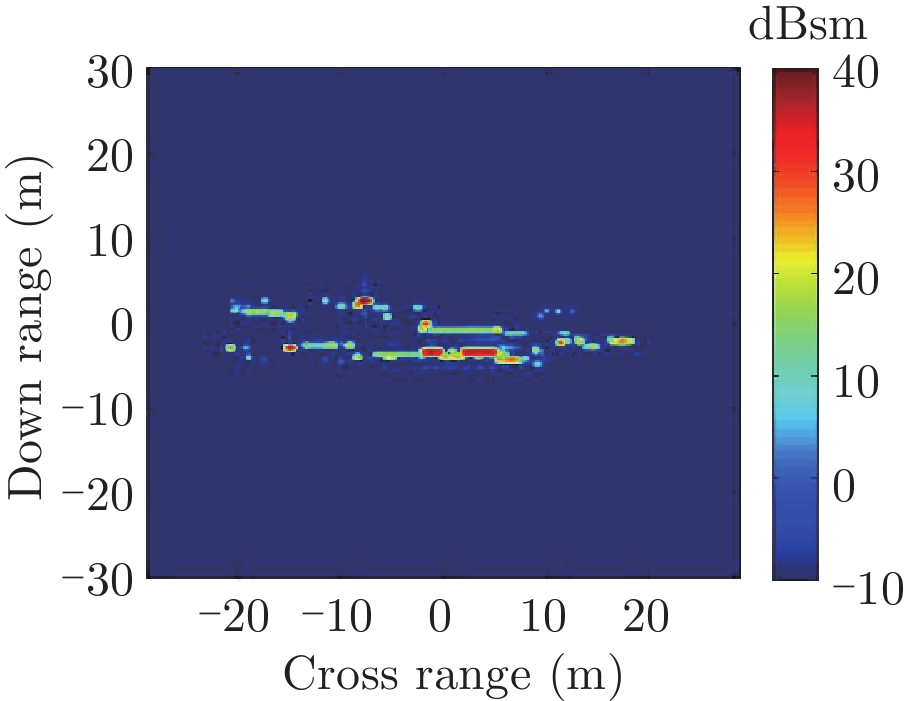
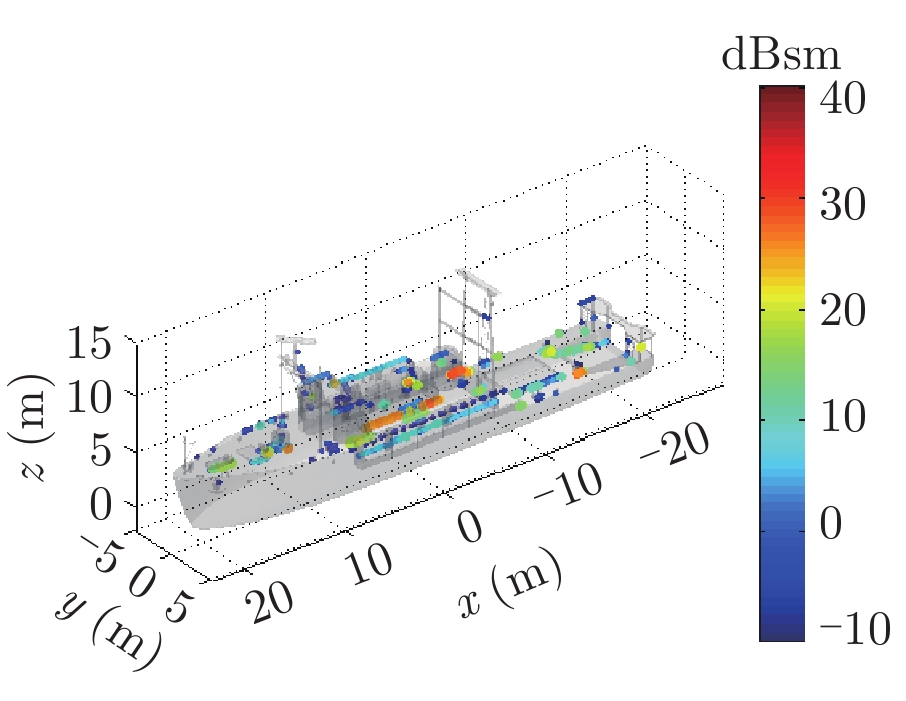
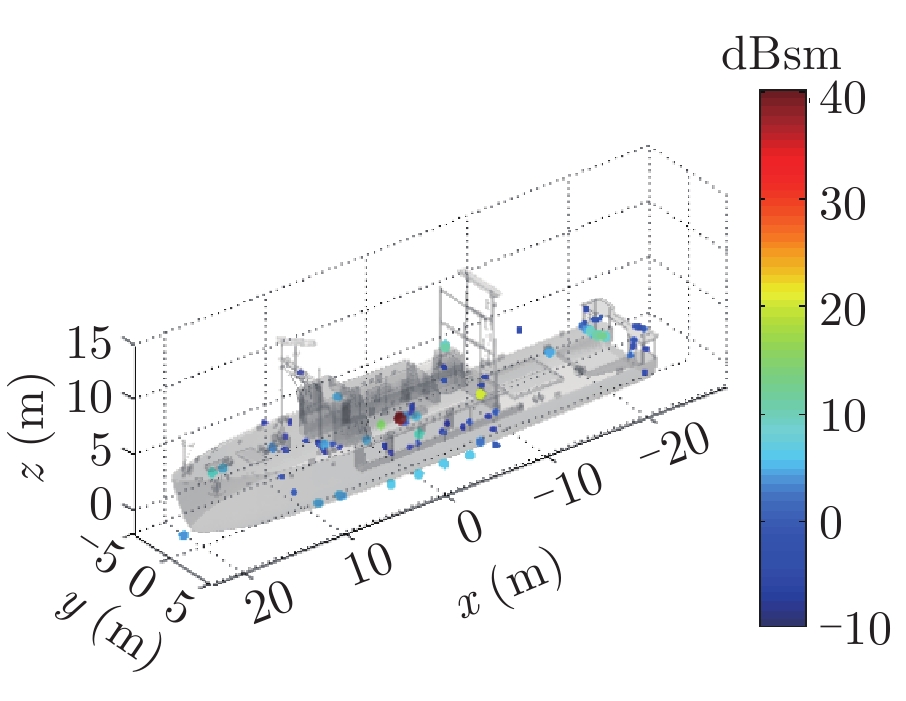
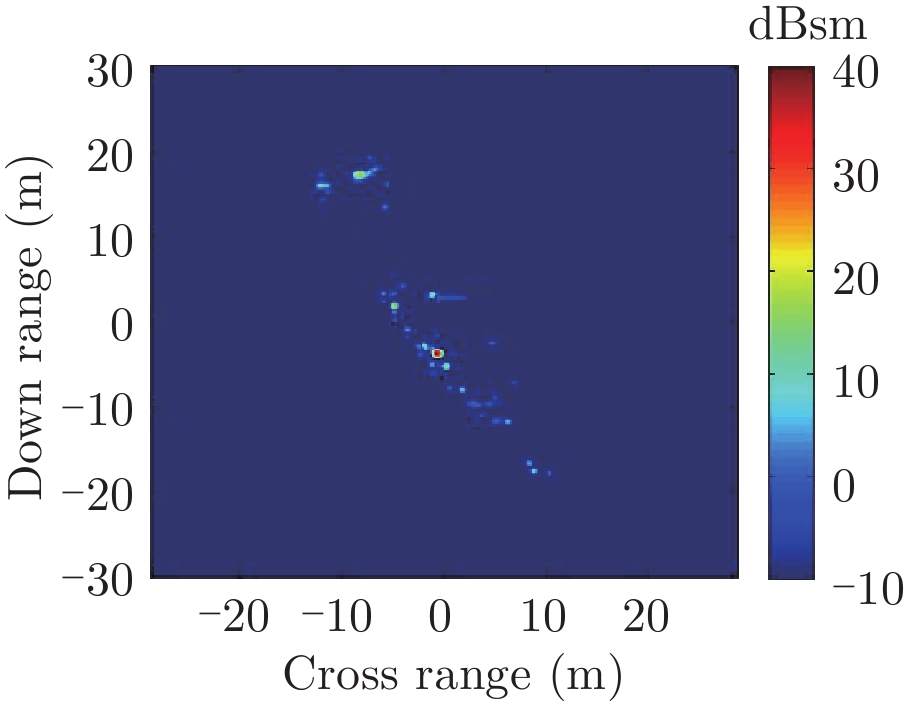
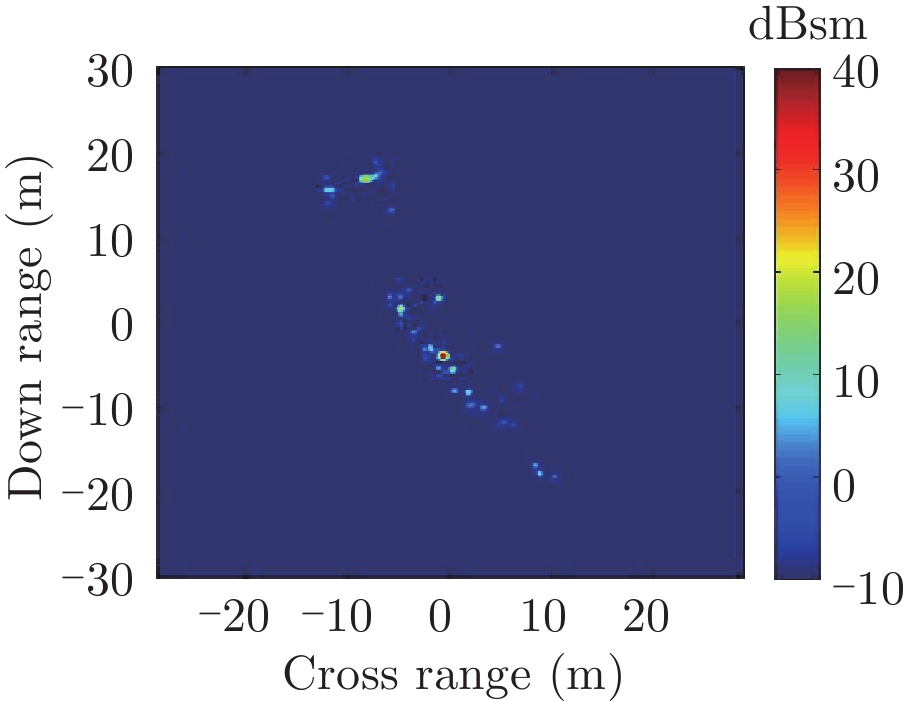
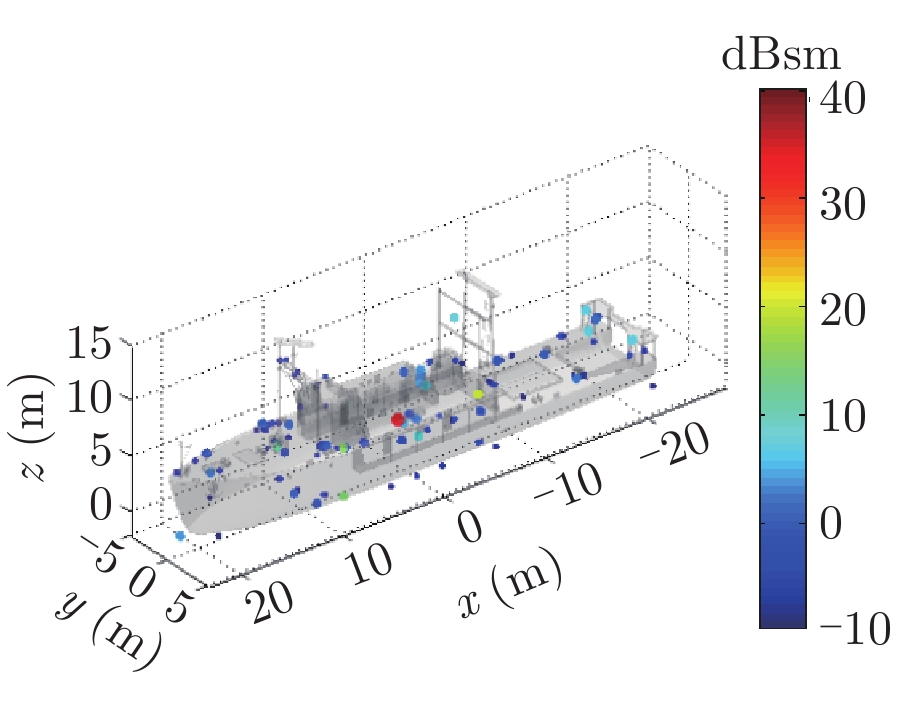
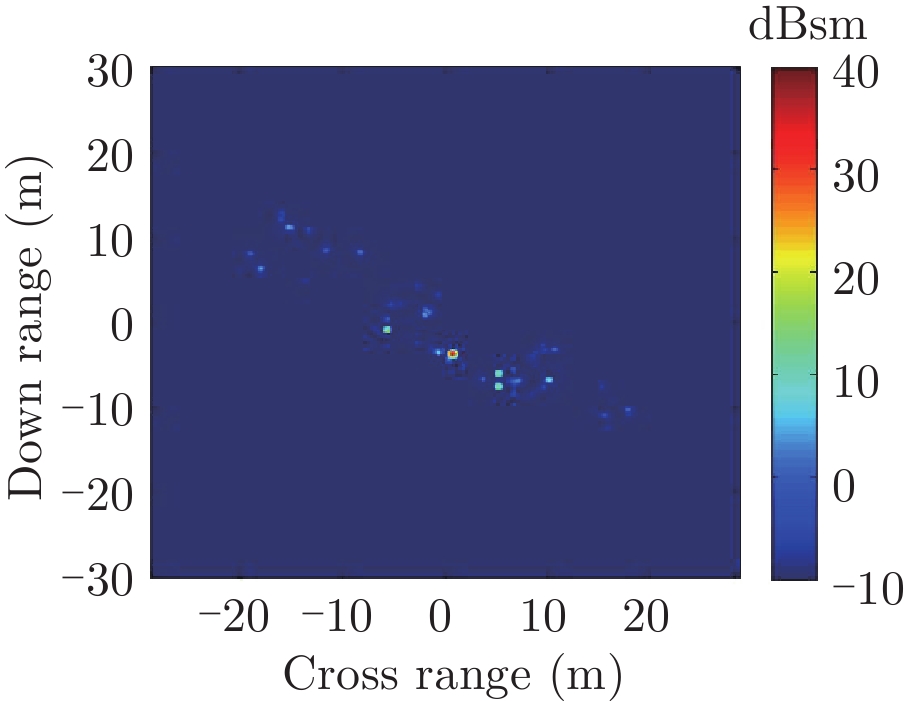
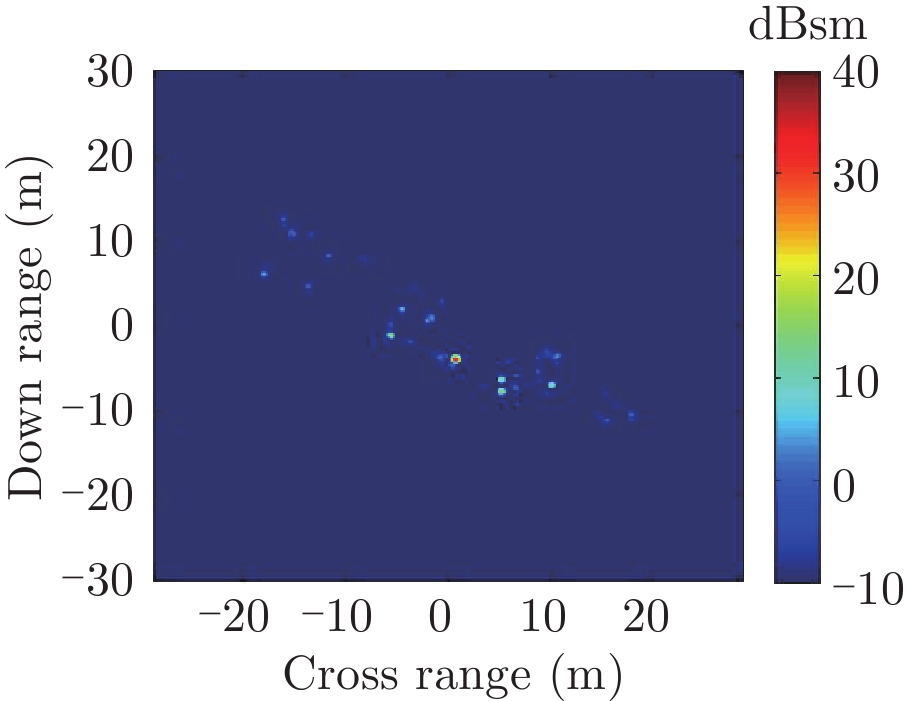
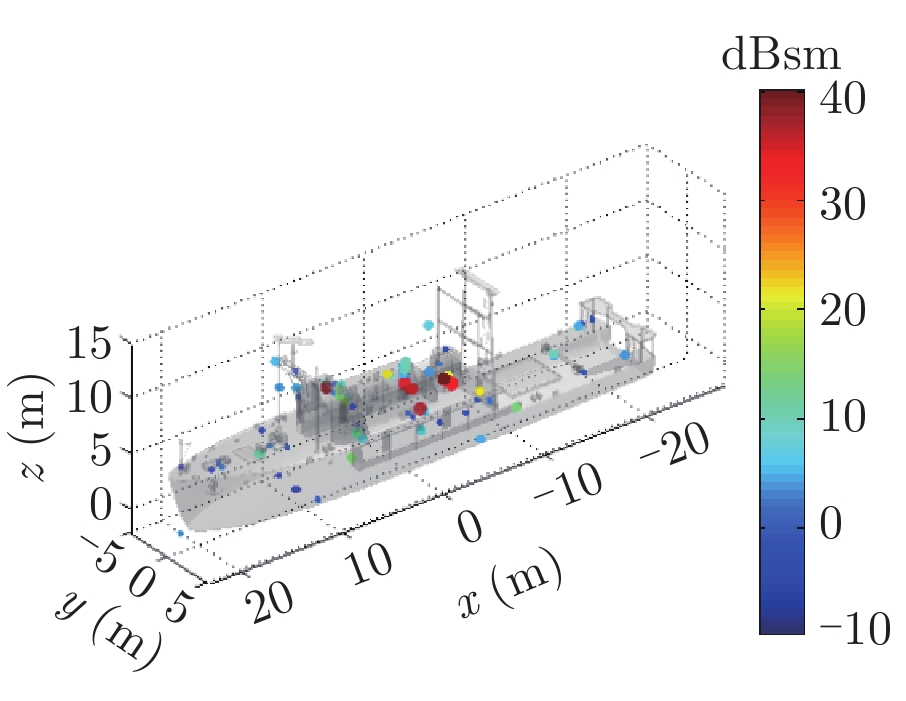
表1给出了1级海情海面上舰船目标3维散射中心分布、仿真的和散射中心重建的1维距离像历程图以及两幅图像的相似度计算。其中3维散射中心分布图是将不同方位的散射中心同时显示,并给出目标的面元模型。图中舰船船舷底部吃水线附近出现的散射中心为舰船-海面耦合散射中心,产生的机理是舰船甲板上与海面形成垂直关系的建筑物侧面与海平面的2次耦合反射。另外,对比仿真的和散射中心重建的1维距离像历程图和相似度计算结果表明,散射中心重建的1维距离像具有较高的精度。其中相似度计算通过式(10)进行计算
| 表 1 全方位(0°~360°)合成显示的3维散射中心模型及其重建的1维距离像历程图的重构度评估 Tab.1 Display of synthesized 3D scattering center model at various azimuth (0°~360°) and comparison of sinograms calculated by direct simulation and rebuilt by the models |

|
其中,F(i, j)指直接仿真计算的1维距离像历程图或2维像所对应的矩阵,G(i, j)指3维散射中心模型重建的1维距离像历程图或2维像,
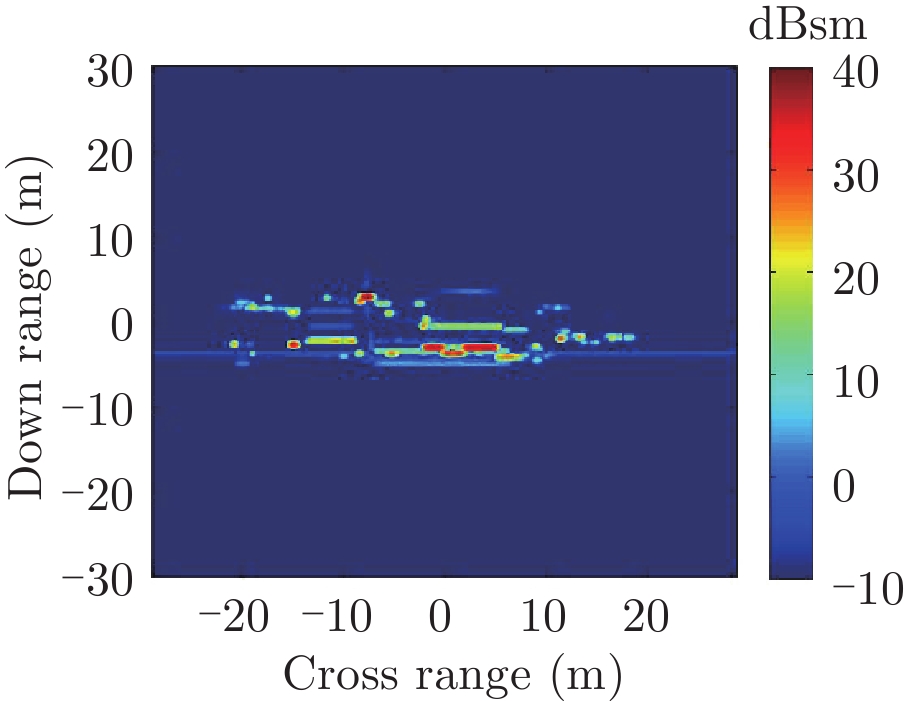
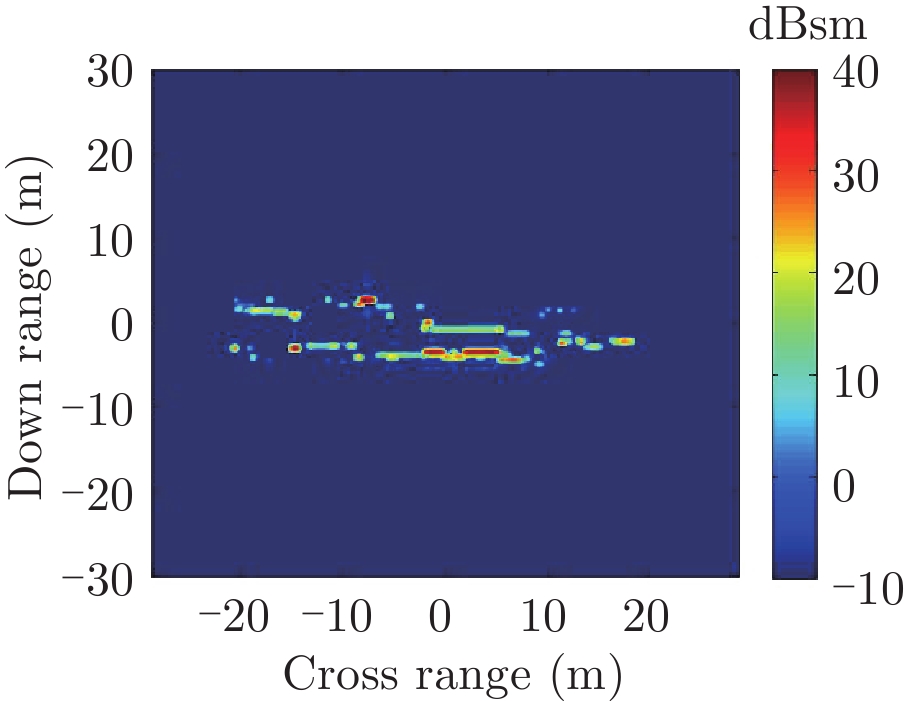
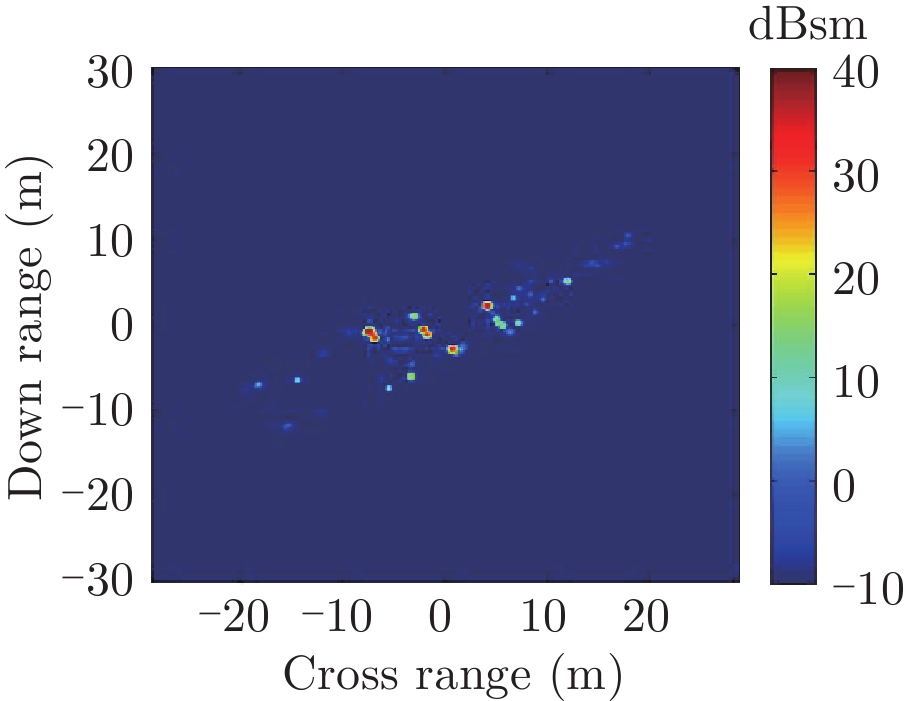
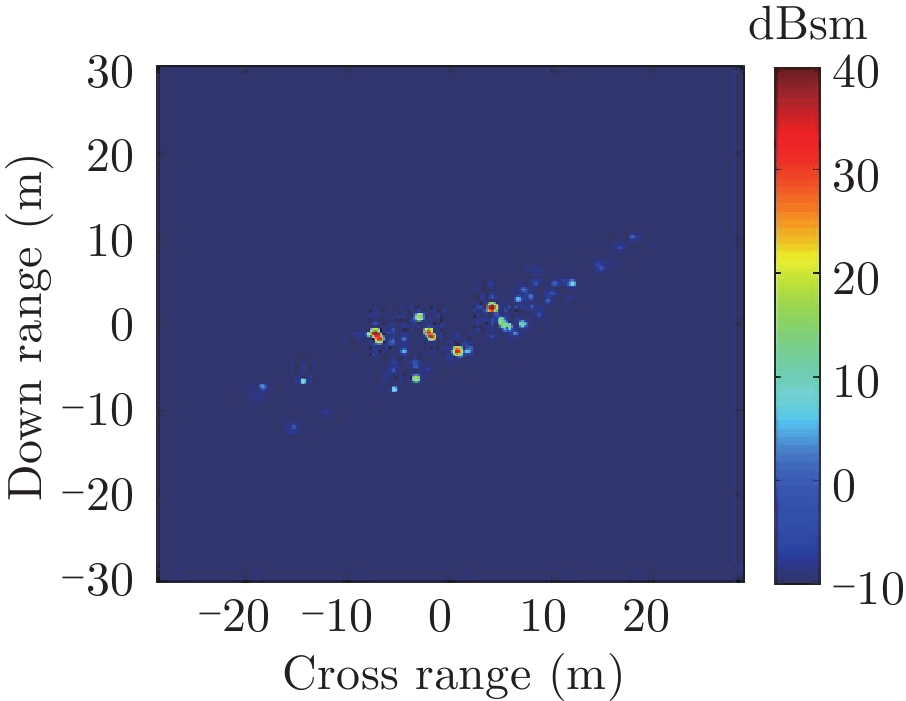
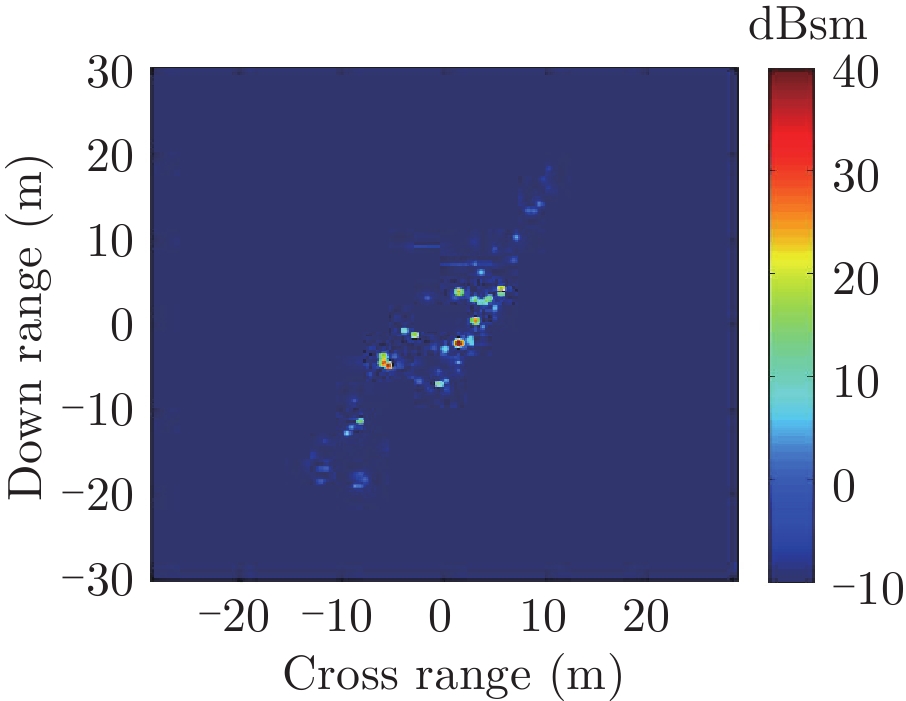
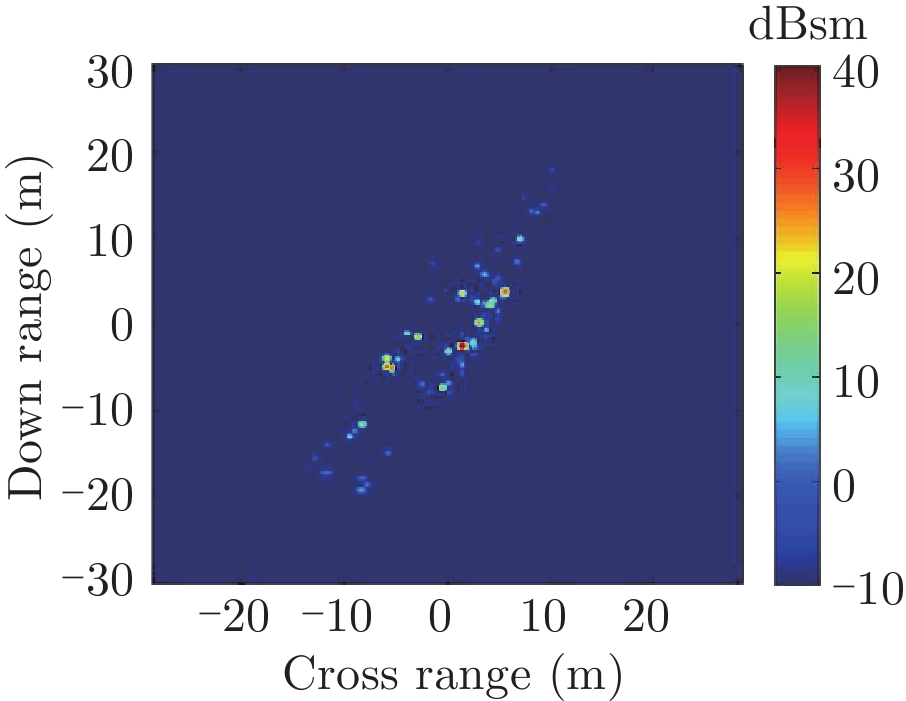
表2中分别给出了入射方位角不变(90°)不同海情(0~3级)下,海面上舰船目标3维散射中心分布、仿真的和散射中心重建的2维像以及两幅图像的相似度计算。对比不同海情的,3维散射中心分布,耦合散射中心(处于船舷吃水线附近)的幅度随着海情的增加而降低,这是由于随着海情增大粗糙海面的反射系数增大所致。表3中则分别给出了海情不变(1级)时,不同方位入射条件下海面上舰船目标3维散射中心分布、仿真的和散射中心重建的2维像以及两幅图像的相似度计算。表2、表3中仿真的和散射中心重建的2维像对比和相似度计算(见(10)式)结果表明,不同海况、入射条件下3维散射中心重建的2维像具有较高的精度。
| 表 2 不同海情下3维散射中心模型及其重建的2维ISAR像重构度评估(方位90°) Tab.2 Display of 3D scattering center models and comparison of ISAR images calculated by direct simulation and rebuilt by the models under different sea conditions at azimuth 90° |
| 表 3 不同入射方位下3维散射中心模型及其重建的2维ISAR像重构度评估(1级海情) Tab.3 Display of 3D scattering center models and comparison of ISAR images calculated by direct simulation and rebuilt by the models at different azimuth under level-1 sea condition |
上述结果说明,本文所提3维散射中心快速建模算法具有较好的计算精度。下面进一步考察本算法的计算效率。
表4给出了本文所提算法与传统算法在确定典型计算条件下的计算耗时对比。采用的计算配置为惠普Z840工作站(处理器:Intel(R) Xeon(R) CPU E5-2687W v3 @ 3.10 GHz(20核);内存:64 GB;NVIDIA Quadro 6000图形处理单元)。结果表明,本文所提基于射线管积分算法(Ray-tube Integration Method, RIM)与传统基于扫频扫角RCS计算和3D-FFT 3维成像算法相比,计算效率至少提高4个数量级。
| 表 4 3维散射中心计算效率对比(以用于计算3维散射中心的3维成像分辨率取0.1 m×0.1 m×0.1 m为例) Tab.4 Comparison of computation time by traditional algorithm and proposed algorithm (take the resolution 0.1 m×0.1 m×0.1 m in 3D images as example) |
需说明的是,3维ISAR像采样间隔将影响CLEAN算法提取散射中心的精度(其中采样间隔大小决定了散射中心位置误差大小),精度要求越高,需要越小的采样间隔(即更高的采样率)。但在实际中采样率不能无限提高,它受到实际计算机内存空间大小的限制。本算例中获取的3维散射中心位置误差为0.1 m的量级,应用于生成高分辨雷达图像,可满足实际工程需求。但如果用于生成RCS或低分辨雷达图像,此时RCS或单个分辨单元内的响应将由多个散射中心进行叠加而获得,由于在当前频率(10 GHz)情况下,0.1 m的散射中心位置误差将导致较大的相位误差,从而使得重建的RCS或低分辨图像的精度下降。对于此问题,根据文献[13],可采用在3个正交方向上生成1维像、提取1维散射中心、重构3维散射中心的方法,来有效地缓解采样率与计算存储空间之间的矛盾,实现更高精度的3维散射中心建模。
5 结论本文提出一种基于射线弹跳追踪技术的海面舰船目标3维散射中心快速建模算法。本算法结合舰船-海面耦合的“4路径”模型、快速生成3维像的射线管积分技术,以及基于修正Fresnel反射系数的海面模型与“准镜面”处理方法,实现了工程上可用的电大、超电大尺寸舰船目标与海面复合的3维散射中心模型数据的快速生成。在不同海况、入射角条件下,与直接仿真计算的1维距离像历程图和2维像结果对比表明,本文所提算法具有较好的精度。本文算法既能用于海面舰船目标特性数据的快速生成,也能用于SAR目标图像模板的在线生成,可避免存储海量的图像模板数据,因此,可有效支撑海面舰船目标自动识别研究与系统研制。
| [1] |
黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2005: 230–237.
Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Signature[M]. Beijing: Publishing House of Electronics Industry, 2005: 230–237. (  0) 0)
|
| [2] |
Keller J B. Geometrical theory of diffraction[J].
Journal of the Optical Society of America, 1962, 52(2): 116-130. DOI:10.1364/JOSA.52.000116 ( 0) 0)
|
| [3] |
Bhalla R and Ling H. A fast algorithm for signature prediction and image formation using the shooting and bouncing ray technique[J].
IEEE Transactions on Antennas and Propagation, 1995, 43(7): 727-731. DOI:10.1109/8.391147 ( 0) 0)
|
| [4] |
Tseng N. A very efficient RCS data compression and reconstruction technique[D]. [Master dissertation], The Ohio State University, 1992.
( 0) 0)
|
| [5] |
Chang L C. Removal of undesired scattering centers using a radar image technique[D]. [Master dissertation], The Ohio State University, 1993.
( 0) 0)
|
| [6] |
Hurst M and Mittra R. Scattering center analysis via Prony’s method[J].
IEEE Transactions on Antennas and Propagation, 1987, 35(8): 986-988. DOI:10.1109/TAP.1987.1144210 ( 0) 0)
|
| [7] |
Garber F D, Chamberlain N F, and Snorrason O. Time-domain and frequency-domain feature selection for reliable radar target identification[C]. Proceedings of the 1988 IEEE National Radar Conference, Ann Arbor, USA, 1988: 79–84. DOI: 10.1109/NRC.1988.10934.
( 0) 0)
|
| [8] |
Dudgeon D E and Lacoss R T. An overview of automatic target recognition[J].
The Lincoln Laboratory Journal, 1993, 6(1): 3-10. ( 0) 0)
|
| [9] |
陈勇, 董纯柱, 王超, 等. 基于HPP/PO的舰船与海面耦合散射快速算法[J].
系统工程与电子技术, 2008, 30(4): 589-592. Chen Yong, Dong Chun-zhu, Wang Chao, et al. Fast algorithm based on HPP/PO for calculating coupling EM scattering from ship over sea surface[J]. Systems Engineering and Electronics, 2008, 30(4): 589-592. DOI:10.3321/j.issn:1001-506X.2008.04.001 (  0) 0)
|
| [10] |
朱炜, 郭航. 现代舰船隐身技术的若干方法研究[J].
舰船电子工程, 2014, 34(12): 22-26. Zhu Wei and Guo Hang. Research on the methods of warship stealthy technology[J]. Ship Electronic Engineering, 2014, 34(12): 22-26. DOI:10.3969/j.issn1672-9730.2014.12.006 (  0) 0)
|
| [11] |
王峰, 徐丰, 金亚秋. 利用序列ISAR图像获取空间目标3-D信息的方法[J].
遥感技术与应用, 2016, 31(5): 900-906. Wang Feng, Xu Feng, and Jin Ya-qiu. 3-D information reconstruction of a space target from 2-D ISAR image sequence[J]. Remote Sensing Technology and Application, 2016, 31(5): 900-906. DOI:10.11873/j.issn.1004-0323.2016.5.0900 (  0) 0)
|
| [12] |
Zhou J X, Shi Z G, Cheng X, et al. Automatic target recognition of SAR images based on global scattering center model[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3713-3729. DOI:10.1109/TGRS.2011.2162526 ( 0) 0)
|
| [13] |
Bhalla R, Ling H, Moore J, et al. 3D scattering center representation of complex targets using the shooting and bouncing ray technique: A review[J].
IEEE Antennas and Propagation Magazine, 1998, 40(5): 30-39. DOI:10.1109/74.735963 ( 0) 0)
|
| [14] |
Zhou J X, Shi Z G, and Fu Q. Three-dimensional scattering center extraction based on wide aperture data at a single eleva-tion[J].
IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1638-1655. DOI:10.1109/TGRS.2014.2346509 ( 0) 0)
|
| [15] |
Potter L C, Chiang D M, Carriere R, et al. A GTD-based parametric model for radar scattering[J].
IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1058-1067. DOI:10.1109/8.467641 ( 0) 0)
|
| [16] |
Potter L C and Moses R L. Attributed scattering centers for SAR ATR[J].
IEEE Transactions on Image Processing, 1997, 6(1): 79-91. DOI:10.1109/83.552098 ( 0) 0)
|
| [17] |
Jackson J A, Rigling B D, and Moses R L. Canonical scattering feature models for 3D and bistatic SAR[J].
IEEE Transac-tions on Aerospace and Electronic Systems, 2010, 46(2): 525-541. DOI:10.1109/TAES.2010.5461639 ( 0) 0)
|
| [18] |
王菁. 光学区雷达目标散射中心提取及其应用研究[D]. [博士论文], 南京航空航天大学, 2010: 3–77. DOI: 10.7666/d.d167227.
WANG Jing. A study on radar optical region target scattering center extraction and its applications[D]. [Ph.D. dissertation], Nanjing University of Aeronautics and Astronautics, 2010: 3–77. DOI: 10.7666/d.d167227. (  0) 0)
|
| [19] |
李飞, 纠博, 刘宏伟, 等. 基于稀疏表示的SAR图像属性散射中心参数估计算法[J].
电子与信息学报, 2014, 36(4): 931-937. Li Fei, Jiu Bo, Liu Hong-wei, et al. Sparse representation based algorithm for estimation of attributed scattering center parameter on SAR imagery[J]. Journal of Electronics & Information Technology, 2014, 36(4): 931-937. DOI:10.3724/SP.J.1146.2013.00576 (  0) 0)
|
| [20] |
Li Z H, Jin K, Xu B, et al. An improved attributed scattering model optimized by incremental sparse Bayesian learning[J].
IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(5): 2973-2987. DOI:10.1109/TGRS.2015.2509539 ( 0) 0)
|
| [21] |
汪雄良, 冉承其, 王正明. 基于紧致字典的基追踪方法在SAR图像超分辨中的应用[J].
电子学报, 2006, 34(6): 996-1001. Wang Xiong-liang, Ran Cheng-qi, and Wang Zheng-ming. Super-resolution processing of SAR images by basis pursuit method based on compacted dictionary[J]. Acta Electronica Sinica, 2006, 34(6): 996-1001. DOI:10.3321/j.issn:0372-2112.2006.06.005 (  0) 0)
|
| [22] |
Tsao J and Steinberg B D. Reduction of sidelobe and speckle artifacts in microwave imaging: The CLEAN technique[J].
IEEE Transactions on Antennas and Propagation, 1988, 36(4): 543-556. DOI:10.1109/8.1144 ( 0) 0)
|
| [23] |
Koets M A and Moses R L. Image domain feature extraction from synthetic aperture imagery[C]. Proceedings of 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing, Phoenix, USA, 1999: 2319–2322. DOI: 10.1109/ICASSP.1999.758402.
( 0) 0)
|
| [24] |
Koets M A and Moses R L. Feature extraction using attributed scattering center models on SAR imagery[C]. Proceedings of SPIE 3721, Algorithms for Synthetic Aperture Radar Imagery VI, Orlando, USA, 1999: 104–115. DOI: 10.1117/12.357628.
( 0) 0)
|
| [25] |
Burkholder R J, Janpugdee P, and Colak D. Development of computational tools for predicting the radar scattering from targets on a rough sea surface[R]. Ohio State: Ohio State University ElectroScience Laboratory, 2001.
( 0) 0)
|
| [26] |
Cui K and Xu X J. EM scattering calculation for complex targets over sea surface[C]. Proceedings of 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, 2005: 101–104. DOI: 10.1109/APS.2005.1552186.
( 0) 0)
|
| [27] |
Dong C Z, Wang C, Wei X, et al.. EM scattering from complex targets above a slightly rough surface[C]. Progress in Elec-tromagnetics Research Symposium 2007, Beijing, China, 2007: 1479–1482.
( 0) 0)
|
| [28] |
董纯柱. 典型环境中复杂目标的电磁散射建模与应用研究[D]. [硕士论文], 中国航天二院研究生院, 2007: 31–58, 61–62.
Dong Chun-zhu. EM scattering modeling and application research of complex targets in the typical environment[D]. [Master dissertation], The Second Academy of China Aerospace, 2007: 31–58, 61–62. (  0) 0)
|
| [29] |
Johnson J T. A study of the four-path model for scattering from an object above a half space[J].
Microwave and Optical Technology Letters, 2001, 30(2): 130-134. DOI:10.1002/mop.1242 ( 0) 0)
|
| [30] |
Johnson J T. A numerical study of scattering from an object above a rough surface[J].
IEEE Transactions on Antennas and Propagation, 2002, 50(10): 1361-1367. DOI:10.1109/TAP.2002.802152 ( 0) 0)
|
| [31] |
Meissner T and Wentz F J. The complex dielectric constant of pure and sea water from microwave satellite observations[J].
IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(9): 1836-1849. DOI:10.1109/TGRS.2004.831888 ( 0) 0)
|